欧拉函数

求证： $\varphi(p) = p-1, ~\forall \text{prime } p$

由质数的定义可知，小于等于$p$ 且 与$p$互质的数，在$[1,p]$中，除了 $p$以外均满足！

注： $\varphi(1) = 1$

求证： $\varphi(mn) = \varphi(m)\varphi(n) \iff \gcd(m,n) = 1$

首先，易知 $\varphi(n) = |\mathbb{Z}_n^{\times}|$ , 即 $\mathbb{Z}_n$ 中 unit(存在关于$\bmod~ n$乘法逆元的元素)的数量

因为 $\mathbb{Z}_{mn} \cong \mathbb{Z}_m \times \mathbb{Z}_n \iff \gcd(m,n) = 1$

所以 $\mathbb{Z}_{mn}$的units $\mathbb{Z}_{mn}^{\times}$ ， 与
$\mathbb{Z}_m \times \mathbb{Z}_n$的 units $(\mathbb{Z}_m \times \mathbb{Z}_n)^{\times}$ 之间存在一个 bijection, 即

$\mathbb{Z}_{mn}^{\times} \cong (\mathbb{Z}_m \times \mathbb{Z}_n)^{\times} = \mathbb{Z}_m^{\times} \times \mathbb{Z}_n^{\times}$

所以 $\varphi(mn) = |\mathbb{Z}_{mn}^{\times}| = |\mathbb{Z}_m^{\times} \times \mathbb{Z}_n^{\times}| = |\mathbb{Z}_m^{\times}||\mathbb{Z}_n^{\times}| = \varphi(m)\varphi(n)$

注：

1. $\mathbb{Z}_{mn} \cong \mathbb{Z}_m \times \mathbb{Z}_n \iff \gcd(m,n) = 1$ 的证明见 这里
2. 更严格的证明需要用到抽代里的中国剩余定理 （以Ring和Ideal表示的）

求证：$\varphi(p^k) = p^k - p^{k-1} = p^k(1-\frac{1}{p})$

$\forall n = p^k$，所有与它不互质的数$m$必然包含$p$这个质数因子，因此满足条件的$m$为：$1p, 2p, 3p, … , p^{k-1}p$，共 $p^{k-1}$个。

所以，与$n = p^k$互质的数共有 $p^k-p^{k-1}$个。

求证：$\forall n = p_1^{k_1}p_2^{k_2}…p_r^{k_r}, ~\varphi(n) = n\prod_{i=1}^{r}(1-\frac{1}{p_i}) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})…(1-\frac{1}{p_r})$

因为 $n = p_1^{k_1}p_2^{k_2}…p_r^{k_r}$，且$p_1,p_2,…,p_r$都是质数（所以两两互质）

由性质2， $\varphi(n) = \varphi(p_1^{k_1})\varphi(p_2^{k_2})…\varphi(p_r^{k_r})$

由性质3，$\varphi(p_i^{k_i}) = p_i^{k_i} - p_i^{k_i-1} = p_i^{k_i}(1-\frac{1}{p_i})$

所以 $\varphi(n) = p_1^{k_1}p_2^{k_2}…p_r^{k_r}(1-\frac{1}{p_1})(1-\frac{1}{p_2})…(1-\frac{1}{p_r}) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})…(1-\frac{1}{p_r})$

求证：$\forall n = p_1^{k_1}p_2^{k_2}…p_r^{k_r}$, 如果 $~\exists ~i, ~s.t. ~k_i > 1$, 则 $\varphi(n) = \varphi(\frac{n}{p_i})*p_i$

因为 $n = p_1^{k_1}p_2^{k_2}…p_r^{k_r}$，

由性质2，$\varphi(n) = \varphi(p_1^{k_1})\varphi(p_2^{k_2})…\varphi(p_r^{k_r})$

由性质3， $\varphi(p^k) = p^k - p^{k-1}$, 我们可以推出 $\varphi(p^{k+1}) = \varphi(p^{k}) * p$

因为 $~\exists ~i, ~s.t. ~k_i > 1$，由上可得出 $\varphi(p_i^{k_i}) = \varphi(p_i^{k_i-1}) * p_i$

即 $\varphi(n) = \varphi(p_1^{k_1})\varphi(p_2^{k_2})… (\varphi(p_i^{k_i-1})*p_i)…\varphi(p_r^{k_r}) = \varphi(\frac{n}{p_i})*p_i$

题目链接: https://www.luogu.com.cn/problem/P2158

#include <bits/stdc++.h>
using namespace std;

const int mod = 998244352;
const int maxn = 4e4+5;

int phi[maxn];
bool p[maxn];
vector<int> primes;

int main() {
    int n; cin >> n;
    if (n <= 1) {
        cout << 0 << endl;
        return 0;
    }
    phi[1] = 1;
    fill(p, p+maxn, 1);

    for (int i = 2; i <= n; i++) {
        if (p[i]) {
            phi[i] = i-1;
            primes.push_back(i);
        }

        for (int j = 0; j < primes.size() && i * primes[j] <= n; j++) {
            int cur = primes[j];
            p[i*cur] = 0;
            if (i % cur == 0) {
                phi[i*cur] = phi[i] * cur;
                break;
            } else {
                phi[i*cur] = phi[i] * phi[cur];
            }
        }
    }
    
    int ans = 3;
    for (int i = 2; i <= n-1; i++) ans += 2*phi[i];
    cout << ans << endl;
    
}

设 $g = \gcd(a,m)$，则 $g = \gcd(a+x,m)$，所以 $\gcd(\frac{a+x}{g}, \frac{m}{g}) = 1~$ 且 $~g|(a+x)$，又因为 $g|a$，所以 $~g|x$

所以问题转化为：

设 $c = \frac{a}{g}, x = \frac{m}{g}$，求 $k \in [c,c+x)$，使得 $k$ 满足：$gcd(x, k) = 1$ 的 $k$ 的数量？

我们会发现当 $k > x$ 时，因为 $\gcd(x,k) = \gcd(x, k-x)$，所以我们可以将 $k \in (x,c+x)$ 的这一段，映射到 $k \in (0,c)$ 上。

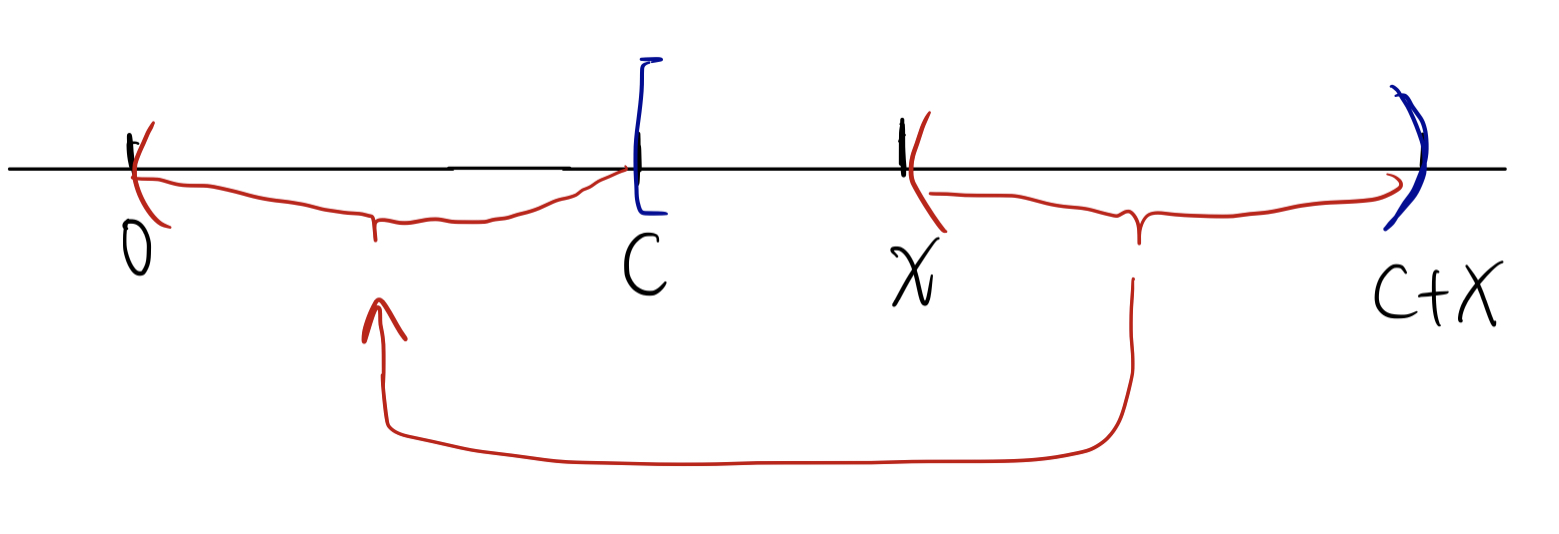
所以最后我们要求的$k$就是： $k \in [1,x]$ 使得 $\gcd(k, x) = 1$，所以满足条件的 $k$ 的数量就等于 $\varphi(x)$

先考虑 $f(k)$：有多少个点对 $i<j$ 满足 $\gcd(i,j)=k$？

注意到 $\gcd(i,j)=k \iff i=ak, j=bk$ 且 $\gcd(a,b)=1$。

所以要求 $\gcd(i,j)=k$ 的点对数量，令 $m = \frac{n}{k}$。

则我们所求的变成 $1…m$ 中互质的数对的数量。

形式化的，求：

$$\sum\limits_{i=1}^m \sum\limits_{j=1}^{i-1} [1|gcd(i,j)=1]$$

注意到如果我们固定 $i$，那么里面那层求和就是欧拉函数 $\phi(i)$，也就是求

$$\sum\limits_{i=1}^m \phi(i)$$

这个预处理出来就可以了。

接下来考虑最少加几次边可以得到 $m$？

$m$ 超级大所以没法背包。但注意到对于每一个 $k$，我们都至少可以加一次。

有了这个性质，说明只要 $m$ 小于等于最大可能加的边数，就一定有解（可以理解成 $1,2,4,8…$ 这种构成了二进制的basis，覆盖了所有数，那这个更密集的 $k$ 一定也可以）。

所以贪心的从大往小加，就可以得到最少加边次数了。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
const int M = 1e6;
 
int phi[maxn];
ll sum_phi[maxn];
bool p[maxn];
vector<int> primes;
ll cnt[maxn];
 
void solve(int n, ll m) {
    for (int k = 2; k <= n; k++) {
        cnt[k] = sum_phi[n/k];
    }
    ll ans = 0;
    for (int k = n; k >= 2; k--) {
        // weight = k, cost = k, add (k-1) edges
        ll r = min(cnt[k], m) / (k-1);  // 拿了 r 次
        ans += r * k;
        m -= r * (k-1);
        if (!m) {
            cout << ans << "\n";
            return;
        }
    }
    cout << -1 << "\n";
}
 
int main() {
    int T; cin >> T;
 
    phi[1] = 0;
    fill(p, p+maxn, 1);
    for (int i = 2; i <= M; i++) {
        if (p[i]) {
            phi[i] = i-1;
            primes.push_back(i);
        }
        for (int j = 0; j < primes.size() && i * primes[j] <= M; j++) {
            int cur = primes[j];
            p[i*cur] = 0;
            if (i % cur == 0) {
                phi[i*cur] = phi[i] * cur;
                break;
            } else {
                phi[i*cur] = phi[i] * phi[cur];
            }
        }
    }
 
    for (int i = 1; i <= M; i++) {
        sum_phi[i] = sum_phi[i-1] + phi[i];
    }
 
    while (T--) {
        int n; ll m; cin >> n >> m;
        solve(n, m);
    }
}