树形dp
Contents
介绍
树形dp就是在树上进行dp,常用于 “树上选一组点/边,满足某些条件,且使得某些权值和最大” 的问题。
一般来说,DP的形式为:
设 $dp[i][j]$ 为: 以 $i$ 为根的子树当中,选了 $j$ 个元素得到的最大值。
这样,状态转移就有:
$$dp[u][j] = \max\limits_{to} \{ dp[u][j-k] + dp[to][k]\}$$
代码如下:
for (int j = m; j >= 1; j--) {
for (int k = 1; k <= j-1; k++) {
dp[cur][j] = max(dp[cur][j], dp[cur][j-k] + dp[nei][k]);
}
}
需要注意的点:
- 类似于 $01$ 背包,在枚举
j的值时,要从大到小,防止一个child被重复选择。 - 对于依赖关系(例如,child需要依赖parent),可以利用DP过程中,调整状态转移的 上下限 来达到!
时间复杂度:$O(nm^2)$,其中 $n$ 为节点数,$m$ 为第二维的大小。
优化
子树 size 优化
对于一个子树,可能它第二维的上限并没有这么高,我们需要尽量避免枚举一些无用的范围。
我们可以优化一下:
对于每一个root节点 cur,我们记录一下 int sz[cur],代表 以cur为根的子树的节点数量, 这样枚举的时候我们就可以优化成这样:
for (int j = min(m, sz[cur]); j >= 1; j--) { //优化
for (int k = 1; k <= min(j-1, sz[nei]); k++) { //优化
dp[cur][j] = max(dp[cur][j], dp[cur][j-k] + dp[nei][k]);
}
}
例题可见 例1
复杂度:$O(nm)$
DFS序 + 背包 优化
有的时候,第二维表示的不一定是 选择 $j$ 个元素,而可能是背包的一个容量,此时上面的优化的效果就不显著了。
我们可以利用 DFS序 进行优化。
令 $i$ 为 $u$ 的DFS序编号,则对于当前节点 $u$,我们有两种选择:
-
选择当前节点:$dp[i+1][j+w_u] = \max \{dp[i][j] + v_u \}$
-
不选当前节点:$dp[i + sz_i][j] = \max \{ dp[i][j]\}$
• 第一维度是选到了dfs序中的前 $i$ 项,第二维度就是背包的容量。
解释:
如果选择当前节点,说明可以继续往子树里传递,所以传递到 $dp[i+1][j+w_u]$。
如果不选择当前节点,由于依赖关系,就必须跳过子树,所以传递到 $dp[i + sz_i][j]$。
最终的答案就是 $ans = \max\limits_{j=0}^m \{dp[n+1][j] \}$。
复杂度:$O(nm)$
例题可见 例2
例题
例1 洛谷P2014
题意
有 $N$ 门课程,每门课程有 $1$ 或 $0$ 门前置课程,需要上了前置课程才能上这门课。每门课 $i$ 有 $s_i$ 学分。
现要选 $M$ 门课,使得学分总和最大。
题解
设 $dp[i][j]$ 为: 以 $i$ 为根的子树当中,选了 $j$ 个课程得到的最大值
根据前置课程的关系建图(会发现这是一棵树),因为有前置课程,所以必须选了root才能选别的,故:
$$dp[i][1] = s_i$$
在处理某一个节点i的时候,$dp[i][j]$ 代表的是: 以它为root的 “已探索” 子树中的最大值,所以在探索各个子树过程中有:
$dp\left[cur\right]\left[j\right]=\max\left(dp\left[cur\right]\left[j\right],dp\left[cur\right]\left[k\right]+dp\left[nei\right]\left[j-k\right]\right),\ k=\left[1,j-1\right]$
实现细节
- 我们利用 $dp[i][1] = s_i$ 来处理前置课程,是非常高效的做法!
- 状态转移的时候,要 倒序枚举 $j$, 也就是 $j = m … 1$, 因为此时 $dp[cur][k]$ 代表的是已探索的部分,不能包括 $nei$ (因为 $nei$ 正在被探索)。为了防止同一个 $nei$ 被考虑多次,要倒序枚举!
- 给定的图可能是一个森林,所以创建一个超级root $0$,并且将 $M$++ (因为 $0$ 肯定要包含进去),最终答案就是 $dp[0][M+1]$
算法优化
注意,在dp状态转移的时候,我们可能用的是如下loop:
for (int j = m; j >= 1; j--) {
for (int k = 1; k <= j-1; k++) {
dp[cur][j] = max(dp[cur][j], dp[cur][j-k] + dp[nei][k]);
}
}
每个节点 cur 都这样loop一次,总复杂度是 $O(nm^2)$,看起来不可接受。
我们可以优化一下:
对于每一个root节点 cur,我们记录一下 int sz[cur],代表 以cur为根的子树的节点数量, 这样枚举的时候我们就可以优化成这样:
for (int j = min(m, sz[cur]); j >= 1; j--) { //优化
for (int k = 1; k <= min(j-1, sz[nei]); k++) { //优化
dp[cur][j] = max(dp[cur][j], dp[cur][j-k] + dp[nei][k]);
}
}
时间复杂度:$O(n^2)$
证明:我们考虑每一个 nei 被用来转移 的次数,会发现它只会在计算它的 parent 的dp值时才会被拿来统计,又因为每一个节点只有1个parent,所以每个节点对应的子树都只会被统计一次。
所以时间复杂度就是 $T(\sum\limits_{i=1}^n i * sz[i]) = O(n^2)$
更严谨的数学证明可以参见 https://www.luogu.com.cn/blog/Chenxiao-Yan/solution-p4322
luogu-P2014-AC代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 305;
const int maxm = 305;
int n,m;
int s[maxn];
int dp[maxn][maxn];
int sz[maxn]; //记录i的子树大小
struct Edge {
int to, nxt;
} edges[maxm];
int head[maxn], ecnt = 1;
void add(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void init() {
scanf("%d%d",&n,&m);
fill(head, head+n+2, -1); //因为存在编号为0的节点,所以初始化为-1
for (int i = 1; i <= n; i++) {
int sc,k;
scanf("%d%d",&k,&sc);
s[i] = sc;
add(k, i);
}
}
void dfs(int cur, int par) {
if (sz[cur]) return; // visited
dp[cur][1] = s[cur];
sz[cur] = 1;
for (int e = head[cur]; ~e; e = edges[e].nxt) {
int nei = edges[e].to;
if (par == nei) continue;
dfs(nei, cur);
sz[cur] += sz[nei];
for (int j = min(m, sz[cur]); j >= 1; j--) { //优化
for (int k = 1; k <= min(j-1, sz[nei]); k++) { //优化
dp[cur][j] = max(dp[cur][j], dp[cur][j-k] + dp[nei][k]);
}
}
}
}
int main() {
init();
m++;
dfs(0, -1);
printf("%d\n", dp[0][m]);
}
如果每门课的前置课程不止1门,就不再是一棵树了,这样的话似乎可以用状压dp来解,leetcode某次比赛中出现过。
例2 洛谷P2515 [HAOI2010]软件安装
题意
给定 $N$ 个软件,每个软件 $i$ 要占用 $W_i$ 的空间,价值为 $V_i$,并且每个软件 $i$ 会依赖最多一个软件 $D_i$。
如果要安装软件 $i$,必须要安装所有的直接/间接依赖软件。
电脑的空间为 $M$,求最大价值。
其中,$1 \leq N \leq 100, 0 \leq M \leq 500, 0 \leq W_i \leq M, 0 \leq V_i \leq 1000, D_i \in [0,N], D_i \neq i$
题解
注意到,本题可能有 循环依赖。
对于循环依赖,直接用 SCC 缩点,剩下的就是一个标准的有依赖背包(本质上,树形DP)问题了:
如果 $i$ 依赖 $D_i$,那么将 $D_i$ 所在的 SCC 连一条有向边,指向 $i$ 所在的 SCC 即可。
另外需要注意,本题可能是一个森林。所以缩点后,对于所有入度为 $0$ 的点 $u$,需要用 $0$ 连一条有向边指向 $u$。
最后,从 $0$ 开始 DP 即可。
DP 的核心代码:
void dfs(int u) {
if (wei[u] <= m) dp[u][wei[u]] = val[u];
for (int to : adj2[u]) {
dfs(to);
for (int i = m; i >= wei[u]; i--) {
for (int j = wei[to]; j <= i - wei[u]; j++) {
dp[u][i] = max(dp[u][i], dp[u][i-j] + dp[to][j]);
}
}
}
}
注意几点:
dp[u][wei[u]] = val[u];放在最前面。- DP的过程中,类似于 $01$ 背包,$i$ 是从大到小的,并且下限是
wei[u]。 - DP的过程中,$j$ 的下限是
wei[to],上限是i - wei[u](因为i-j的有效值必须 $\geq$wei[u])。
• 另外,别忘记 tarjan 过程中,更新 low[] 要判断是否在栈内。
树形DP(无优化版本)代码
#include <bits/stdc++.h>
using namespace std;
int n, m, w[105], v[105], d[105];
int dp[103][503];
vector<int> adj1[103];
set<int> adj2[103];
int dfn[103], low[103], id = 0, st[103], tail = -1;
bool in[103];
int from[103], scc = 0;
void tarjan(int u) {
in[u] = 1;
st[++tail] = u;
dfn[u] = low[u] = ++id;
for (int to : adj1[u]) {
if (!dfn[to]) {
tarjan(to);
low[u] = min(low[u], low[to]);
} else if (in[to]) { // 注意这里有 in[to]
low[u] = min(low[u], dfn[to]);
}
}
if (low[u] == dfn[u]) {
from[u] = ++scc;
while (tail >= 0 && st[tail] != u) {
int cur = st[tail--];
in[cur] = 0;
from[cur] = scc;
}
tail--;
in[u] = 0;
}
}
void init() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i];
for (int i = 1; i <= n; i++) cin >> v[i];
for (int i = 1; i <= n; i++) {
cin >> d[i];
if (d[i] == 0) continue;
adj1[d[i]].push_back(i);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) tarjan(i);
}
}
int wei[103], val[103], ind[103];
void rebuild() {
for (int i = 1; i <= n; i++) {
int fu = from[i];
wei[fu] += w[i];
val[fu] += v[i];
int fv = from[d[i]];
if (fu == fv || fv == 0) continue;
adj2[fv].insert(fu);
ind[fu]++;
}
for (int i = 1; i <= scc; i++) {
if (!ind[i]) adj2[0].insert(i);
}
}
void dfs(int u) {
if (wei[u] <= m) dp[u][wei[u]] = val[u];
for (int to : adj2[u]) {
dfs(to);
for (int i = m; i >= wei[u]; i--) { // 注意从大到小,注意下限
for (int j = wei[to]; j <= i - wei[u]; j++) { // 注意上下限
dp[u][i] = max(dp[u][i], dp[u][i-j] + dp[to][j]);
}
}
}
}
int main() {
init();
rebuild();
dfs(0);
int ans = 0;
for (int i = 0; i <= m; i++) ans = max(ans, dp[0][i]);
cout << ans << endl;
}
DFS序 优化
我们可以利用 DFS序 进行优化,让时间复杂度从 $O(nm^2)$ 降到 $O(nm)$。
令 $i$ 为 $u$ 的DFS序编号,则对于当前节点 $u$,我们有两种选择:
-
选择当前节点:$dp[i+1][j+w_u] = \max \{dp[i][j] + v_u \}$
-
不选当前节点:$dp[i + sz_i][j] = \max \{ dp[i][j]\}$
解释:
如果选择当前节点,说明可以继续往子树里传递,所以传递到 $dp[i+1][j+w_u]$。
如果不选择当前节点,由于依赖关系,就必须跳过子树,所以传递到 $dp[i + sz_i][j]$。
最终的答案就是 $ans = \max\limits_{j=0}^m \{dp[n+1][j] \}$。
另外需要注意,由于依赖问题,我们需要 记录每一个节点 $u$ 的所有ancestor的权值和,在枚举的时候,将下限设置为这个权值和。(在代码中,pre[u] 代表 $u$ 所有ancestor的权值和。)
优化代码
// 注意 idcnt = -1,因为我们是从 0 开始 DFS的!
int mp[103], idcnt = -1, sz[103]; // mp[i]: DFS序为 i 的节点编号 u
int pre[103]; // pre[u] 代表 u 的 ancestor 的 weight的和
void dfs(int u) {
mp[++idcnt] = u;
sz[u] = 1;
for (int to : adj2[u]) {
pre[to] = pre[u] + wei[u]; // ancestor的权值和
dfs(to);
sz[u] += sz[to];
}
}
void solve() {
for (int i = 1; i <= scc; i++) {
int u = mp[i];
for (int j = pre[u]; j <= m; j++) { // 注意枚举下限从 pre[u] 开始
dp[i+sz[u]][j] = max(dp[i+sz[u]][j], dp[i][j]); // 不选
if (j + wei[u] <= m) // 选择(要保证 j+wei[u] <= m)
dp[i+1][j+wei[u]] = max(dp[i+1][j+wei[u]], dp[i][j] + val[u]);
}
}
}
int main() {
init();
rebuild();
dfs(0);
solve();
int ans = 0;
for (int j = 0; j <= m; j++) ans = max(ans, dp[scc+1][j]); // 注意是 scc+1
cout << ans << endl;
}
例3 洛谷P4395 [BOI2003]Gem 气垫车
题意
给一棵 $n$ 个节点的树,要求给所有节点标上正整数权值,使得相邻节点不能权值相同,求最小总权值。
其中,$n \leq 10^4$。
题解
第一眼看过去是个树染色问题,要么权值为 $1$,要么为 $2$。
很遗憾这个做法是错的,考虑一下这个数据,两个菊花接在一起:
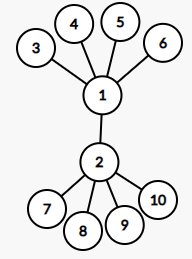
这里很明显应该给 $1,2$ 分别标上 $2,3$ 的权值,其余全部标 $1$。
所以我们暴力枚举一下每个节点上可能标什么权值就好了,直觉上告诉我们这个上限不会太大。
然后利用树形DP来求最小值即可。
代码中取了上限 $M = 55$,所以复杂度就是 $O(55^2 * n)$
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10005;
const int M = 55;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1, n, m;
int dp[maxn][M+3];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
void dfs(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
for (int j = 1; j <= M; j++) {
int r = 1e9;
for (int k = 1; k <= M; k++) {
if (j == k) continue;
r = min(r, dp[to][k]);
}
dp[u][j] += r;
}
}
for (int j = 1; j <= M; j++) dp[u][j] += j;
}
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v);
addEdge(v,u);
}
dfs(1, 0);
int ans = 1e9;
for (int j = 1; j <= M; j++) ans = min(dp[1][j], ans);
cout << ans << endl;
}
例4 洛谷P3177 [HAOI2015]树上染色
题意
给定一棵 $n$ 个节点的树,树的边上有权值。
给定一个整数 $k \in [0,n]$,要求从树上选择 $k$ 个点,将其染成黑色,剩余的染成白色。
染色后,获得的价值为 黑点两两之间的距离之和 + 白点两两之间的距离之和。
求最大价值?
其中,$n,k \leq 2000$。
题解
数据范围看起来就非常树形DP。
设 dp[u][i] 为在 $u$ 的子树内,染 $i$ 个黑点的总价值。
现在考虑一下怎么转移?
如果我们直接进行转移,就需要维护节点的深度之和,然而这很明显不现实,所以我们可以 考虑每条边 的贡献。
假设考虑的子树 $v$ 中,染了 $j$ 个黑点,那么一条边 $(u,v,w)$ 的贡献刚好就是:
$$w * (j * (k-j) + (sz[to] - j) * (n - k - sz[to] + j))$$
其中 j * (k-j) 是这条边两端的黑点数量的乘积,而 (sz[to] - j) * (n - k - sz[to] + j) 就是这条边两端的白点数量的乘积。
然后直接转移就可以了(注意第二维度的转移顺序是从 $0$ 开始,否则会导致 $dp[u][i]$ 被更新两次),注意一下使用 sz[] 进行时间复杂度优化到 $O(n^2)$,否则是 $O(n^3)$。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2003;
ll dp[maxn][maxn];
ll sz[maxn];
int n,k;
struct Edge {
int to, nxt;
ll w;
} edges[maxn<<1];
int ecnt = 1, head[maxn];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
void dfs1(int u, int p) {
sz[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, u);
sz[u] += sz[to];
}
}
void dfs(int u, int p) {
dp[u][0] = dp[u][1] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
ll w = edges[e].w;
for (ll i = (ll)min((ll)k, sz[u]); i >= 0; i--) { // u 用多少个黑
for (ll j = 0; j <= min(i,sz[to]); j++) { // v 用多少个黑
ll cnt = j * (k - j) + (sz[to] - j) * (n - k - sz[to] + j);
dp[u][i] = (ll)max(dp[u][i], dp[u][i-j] + dp[to][j] + cnt * w);
// j = 0 开始: dp[u][i], dp[u][i-1] ... (正确)
// j = min(i,sz[to]) 开始: dp[u][0], dp[u][1], ..., dp[u][i] -> 这导致 dp[u][i] 被更新了两次
}
}
}
}
int main() {
cin >> n >> k;
for (int i = 1; i <= n-1; i++) {
int u,v; ll w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
for (int i = 1; i <= n; i++)
for (int j = 2; j <= k; j++) dp[i][j] = -1e18;
dfs1(1, 0);
dfs(1, 0);
cout << dp[1][k] << endl;
}
注意事项
- 本题枚举 $i,j$ 时,注意要加上 $sz[u], sz[to]$ 作为上限来优化。
- 注意初始化 $dp[i][j]$ 为负无穷,并且设 $dp[i][0] = dp[i][1] = 0$。
- 注意第二维度的转移顺序(第一维倒序这个是必须的)。
例5 [1到n经过特定点的最短路]
题意
给定 $n$ 个节点的一棵树,树上有 $m$ 个点被标记了,求从节点 $1$ 走到节点 $n$,中途需要经过这些标记点的最短路长度,所有边权值为 1。
其中,$n \leq 2 \times 10^5$。
题解
• 这是一道群里传的题目,没有代码。
首先将 $1$ 到 $n$ 的路径拉成一条链,链上所有的点一定会被经过,不用管。
接下来就是挂在链上的若干子树,对于每个子树,思考如下问题:
从一棵树的根出发,经过树内的所有标记点,再回到这棵树的根,需要的最短路长度?
对于这个问题,我们考虑对于每个被标记的点 $u$,从根(假设为 $1$)到 $u$ 的路径一定会被经过,被经过的这些边被打上标记,代表这些边一定会被经过。
打完标记后,我们知道在最优解中,每条边一定会被经过 $2$ 次,所以答案就是标记边 $*2$。
如何打标记?
只要一次dfs即可,每次dfs时判断这个子树里面有没有需要标记的点,如果有,这条边就打上标记。
例6 NAQ2017E. Company Picnic
题意
给定一棵树,每个节点有权值 $w_i$。
定义一组节点为:两个直接相连的节点 $i,j$,这组节点的权值定义为 $\min (w_i,w_j)$。
求选出若干组节点的方法,使得每组节点用到的点各不相同,并且满足选出节点组数最多。
在节点组数量最多的情况下,求出这些节点的权值和最大值。
其中,$2 \leq n \leq 1000, w_i \in [2.2,5.3]$。
题解
这个题需要维护最多节点组数,还要维护权值和最大值。所以 dp 数组维护两个值。
定义 $dp(u,0)$ 为:$u$ 的parent没有选它,$dp(u,1)$ 则是选了它的。
dp 值则是一个pair:<int, double>,代表子树中最大的节点组数,以及对应的最大权值和。
在转移的时候,注意到 $dp(u,1)$ 不能选任何 $dp(v,1)$ 转移。而 $dp(u,0)$ 只能选一个 $dp(v,1)$ 转移(或者也可以不选)。
转移的过程中,优先更新第一个值(节点组数),如果第一个值相等,再更新第二个值(权值和最大值)。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e3+5;
pair<int,double> dp[maxn][2];
vector<string> adj[maxn];
map<string, int> mp;
double sp[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
int rt;
void dfs(int u, int p) {
int cnt = 0, b = 0; // b: 最优转移 1 的点v
double sum = 0;
// 0 的情况
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to;
if (v == p) continue;
dfs(v, u);
cnt += dp[v][0].first;
sum += dp[v][0].second;
if (b == 0) b = v;
else if (dp[v][1].first - dp[v][0].first > dp[b][1].first - dp[b][0].first) {
b = v;
} else if (dp[v][1].first - dp[v][0].first == dp[b][1].first - dp[b][0].first &&
min(sp[u], sp[v]) + dp[v][1].second - dp[v][0].second > min(sp[u], sp[b]) + dp[b][1].second - dp[b][0].second) {
b = v;
}
}
if (!b) return;
cnt -= dp[b][0].first;
cnt += dp[b][1].first;
sum -= dp[b][0].second;
sum += min(sp[u], sp[b]) + dp[b][1].second;
dp[u][0].first = cnt + 1;
dp[u][0].second = sum;
cnt = 0, sum = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to;
if (v == p) continue;
cnt += dp[v][0].first;
sum += dp[v][0].second;
}
dp[u][1].first = cnt;
dp[u][1].second = sum;
if (cnt > dp[u][0].first || (cnt == dp[u][0].first && sum > dp[u][0].second)) {
dp[u][0].first = cnt;
dp[u][0].second = sum;
}
}
int main() {
fastio;
int n; cin >> n;
int id = 0;
for (int i = 1; i <= n; i++) {
string s; cin >> s;
if (!mp.count(s) && s != "CEO") mp[s] = ++id;
double w; cin >> w;
string t; cin >> t;
if (!mp.count(t) && t != "CEO") mp[t] = ++id;
int u = mp[s], v = mp[t];
if (t == "CEO") {
rt = u;
} else {
addEdge(u,v);
addEdge(v,u);
}
sp[u] = w;
}
dfs(rt, -1);
cout << dp[rt][0].first << " " << dp[rt][0].second / dp[rt][0].first << "\n";
}
