最小环

1. 如果这是一个tree ($m = n-1$), 则 (1)很容易找, 只要dfs一下，做一个图的染色 (染成 $0,1$)即可, 最后取 全部的 $0$ 或者 全部的 $1$

2. 如果不是tree, 必然存在cycle, 那么我们可以找到一个最小环, 最小环必然满足 (1) 或者 (2)！（易证）

•怎么找最小环? 用DFS!

1. 维护一个环的长度 len
2. 维护一个 dep[] 数组, 代表每个vertex的depth
3. 维护一个 pre[] 数组, pre[u] 代表dfs过程中 u的parent
4. 维护一个 int c, 代表找到的cycle的 终点!

然后，

1. 从vertex 1开始dfs， dep[to] = dep[cur] + 1 这样来更新 dep[]

2. 当我们找到一个backward edge时, 更新最小环长度

   len = min(len, abs(dep[to] - dep[cur]) + 1))
   

   并且更新c, 使得 c = cur, 然后继续探索！

3. dfs结束后, 直接用

   vector<int> cycle;
   void findcycle() {
       while (len--) cycle.push_back(c), c = pre[c];
   }
   

   即可找到最小环！

时间复杂度：$O(n+m)$

易知，最小环满足这个条件！

如何求最小环？可以用 $N$ 次 DFS！

1. 维护 ed 代表环的终点，维护最小环长度 final
2. 维护一个 dep[] 数组, 代表每个vertex的depth
3. 维护一个 par[] 数组, par[u] 代表dfs过程中 u的parent
4. 维护一个 in[] 数组，代表在dfs过程中，当前的某个vertex是否存在于递归stack中！

dfs过程如下：

int n,m, dep[maxn], par[maxn];
int ans = 1e9, ed = -1, final = 1e8;
vector<int> cycle;
bool in[maxn];

void dfs(int cur) {
    in[cur] = 1;
    dep[cur] = dep[par[cur]] + 1;
    for (int e = head[cur]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (dep[to]) {
            if (in[to]) {  // 必须得在递归栈内
                int res = abs(dep[cur] - dep[to]) + 1;
                if (res < ans) {
                    ans = res;
                    ed = cur;
                }
            }
        } else {
            par[to] = cur;
            dfs(to);
        }
    }
    in[cur] = 0;
}

为什么要加 in[] 数组？

如下图：

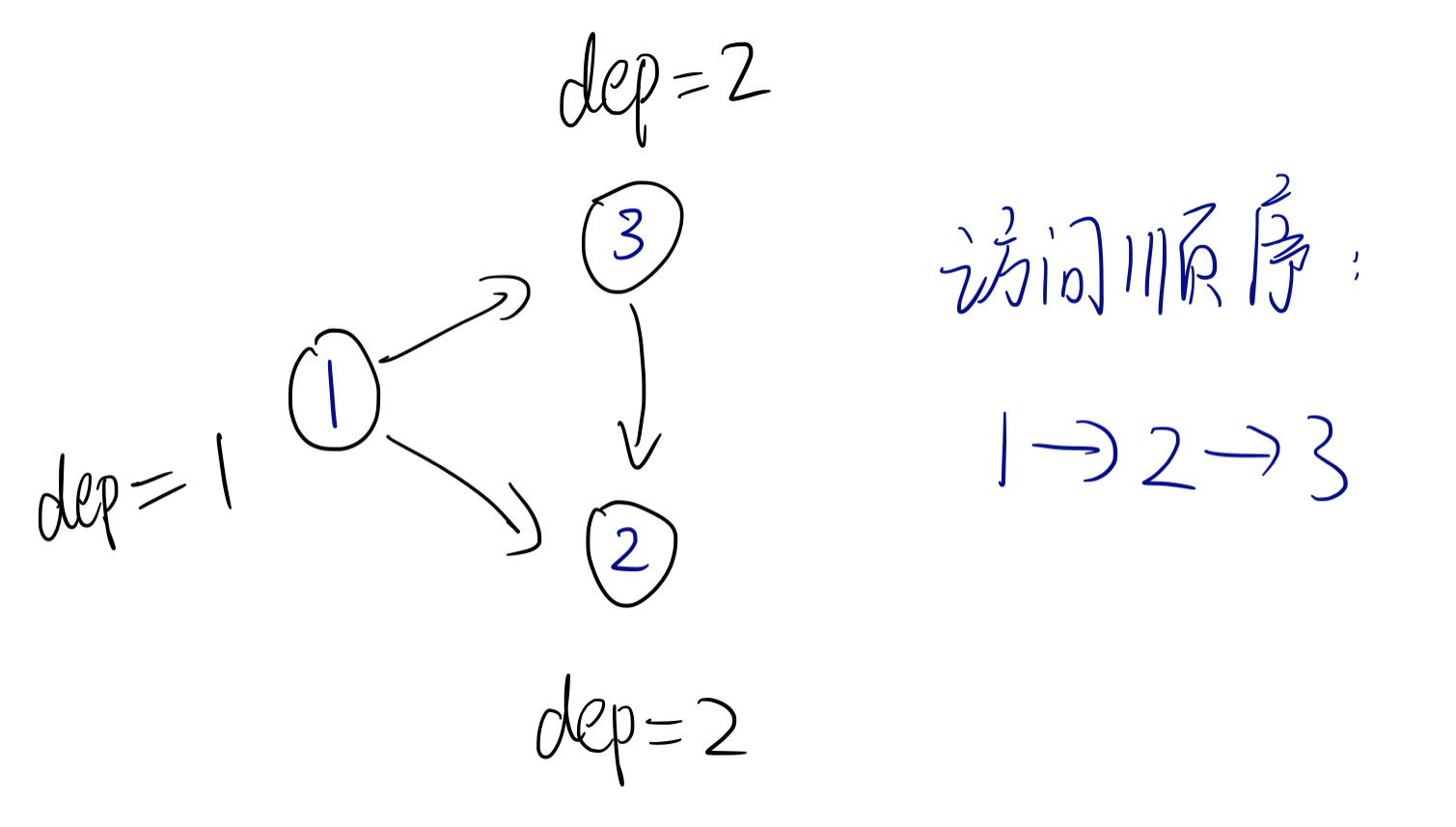
我们需要保证这个环必然全部同时出现在递归stack内，否则可能会出问题！

（如上图，如果不考虑 in[] 数组的话，就有可能错误的把 1->3->2 当作一个环！

为什么要使用 $N$ 次 dfs ？

如下图：

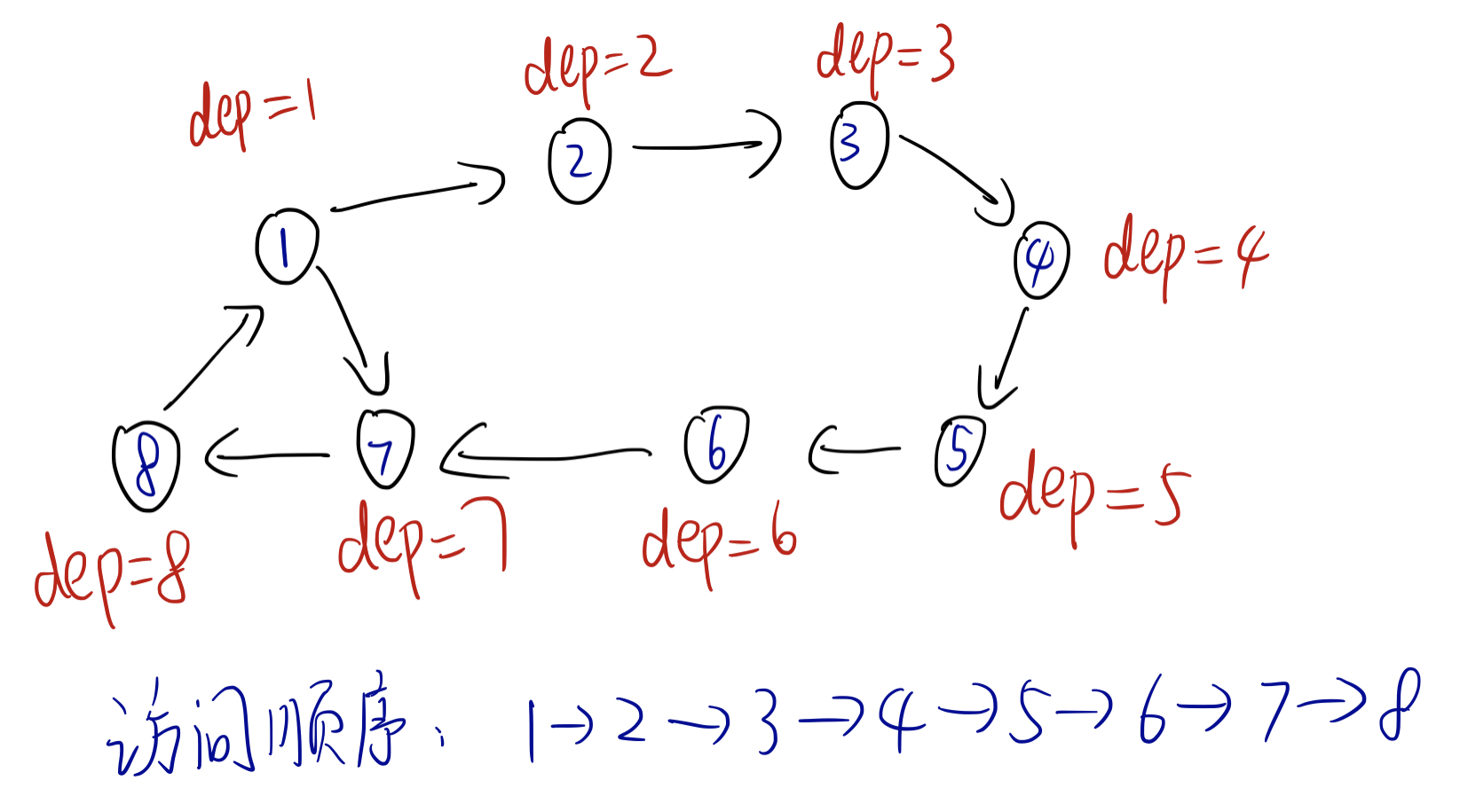
如果我们从 $1$ 开始进行 dfs，那么如果是按照图上的访问顺序，会导致我们找不到最小环！

但是如果从 $7$ 开始进行 dfs，就可以找到了！

所以我们需要每一个点都开始一次dfs，总共 $N$ 次 dfs。

注：优化：可以在每次dfs中找到的环中找最小环，如果不是环中的节点，就不需要考虑了。

using namespace std;
#include <bits/stdc++.h> 

#define abs(a) ((a>0)?a:-(a))

const int mod = 1e9+7;
const int maxn = 1e3+5;
const int maxm = 2e3+10;

struct Edge {
    int to,nxt;
} edges[maxm];
int head[maxn], ecnt = 1;

int n,m, dep[maxn], par[maxn];
int ans = 1e9, ed = -1, final = 1e8;
vector<int> cycle;
bool in[maxn];

void add(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}

void init() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        add(u,v);
    }
}

void dfs(int cur) {
    in[cur] = 1;
    dep[cur] = dep[par[cur]] + 1;
    for (int e = head[cur]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (dep[to]) {
            if (in[to]) {
                int res = abs(dep[cur] - dep[to]) + 1;
                if (res < ans) {
                    ans = res;
                    ed = cur;
                }
            }
        } else {
            par[to] = cur;
            dfs(to);
        }
    }
    in[cur] = 0;
}

void renew() {
    fill(dep, dep+n+1, 0);
    fill(par, par+n+1, 0);
    fill(in, in+n+1, 0);
    ans = 1e9;
}

int main() {
    fastio;
    init();

    for (int i = 1; i <= n; i++) {
        dfs(i);
        if (ans < final) {
            final = ans;
            cycle.clear();
            while (ans--) cycle.push_back(ed), ed = par[ed];
        }
        renew();
    }

    if (final == 1e8) cout << -1 << endl;
    else {
        cout << final << "\n";
        for (int a : cycle) cout << a << "\n";
    }
}