树链剖分
Contents
介绍
树链剖分主要用于将 树上修改/查询 通过 DFS序 变成 区间修改/查询,然后利用 线段树 进行修改/查询。
我们可以用模版来举个例子:
题意
已知一棵包含 $N$ 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
$1\ x\ y\ z$ :将树从 $x$ 到 $y$ 结点最短路径上所有节点的值都加上 $z$。
$2\ x\ y$ :求树从 $x$ 到 $y$ 结点最短路径上所有节点的值之和。
$3\ x\ z$ :将以 $x$ 为根节点的子树内所有节点值都加上 $z$。
$4\ x$ :求以 $x$ 为根节点的子树内所有节点值之和。
主要知识点有三个:DFS序,LCA,线段树
前置知识回顾
DFS序
DFS序的作用是,根据DFS的顺序将节点编号,就可以得到以下性质:
- 同一个subtree内的编号是连续的,且parent的编号最小。
- 在从上到下的DFS过程中,一条链上的编号也是连续的,且越靠上,编号越小。
注:记得将原array中的节点权值(或者其他信息) map 到dfs序上的新节点。
LCA(最近公共祖先)
在 LCA 中,寻找共同祖先的过程中,要注意不能往上跳过头了,在树链剖分中也一样,只不过没有采用倍增思想。
线段树
在树链剖分中,线段树的应用并没有什么变化。
概念定义
-
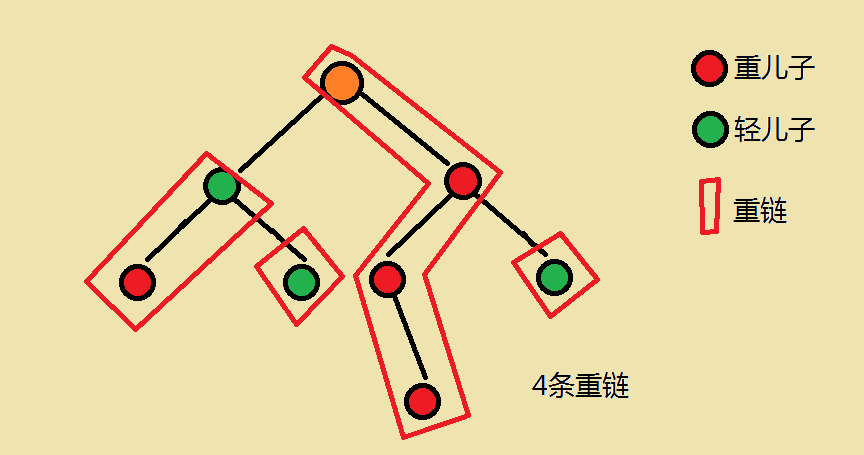
重儿子:每一个节点的child中,所在subtree(包括它自己)节点数最多的child 叫做该节点的重儿子(每个节点有且仅有一个重儿子)。
-
轻儿子:除了重儿子的所有节点,都是轻儿子。(我们可以把 root 看作一个轻儿子)
-
重边:一个节点连接它的重儿子的edge就是重边。
-
重链:以轻儿子作为起点,向下延伸,连接子树内的所有重儿子,形成的链叫做重链。
(对于一个leaf,如果它是一个轻儿子,那么它自己形成一条重链)
算法
算法步骤如下:
- 进行第一次DFS
dfs1() - 进行第二次DFS
dfs2() - 建线段树
- 将树上操作 对应到 区间上,然后用线段树解决
第一次DFS
第一次DFS,我们需要维护的信息有:
- 记录每个点的 深度:
dep[] - 记录每个点的 parent:
par[] - 记录每个点的 subtree大小(包括它自己):
sz[] - 记录每个点的 重儿子:
son[]
int dep[maxn], par[maxn], sz[maxn], son[maxn];
void dfs1(int cur, int p) {
dep[cur] = dep[p] + 1;
par[cur] = p;
sz[cur] = 1; // subtree包括自己
int maxsz = -1;
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, cur);
sz[cur] += sz[to];
if (sz[to] > maxsz) { // 判断重儿子
maxsz = sz[to];
son[cur] = to;
}
}
}
第二次DFS
第二次DFS,我们需要维护的信息有:
- 记录每个点的 DFS序编号:
id[] - 记录每个点 所在重链的最顶端:
top[] - (如果有),将树上的信息通过DFS序编号 转移到 区间上
注意:
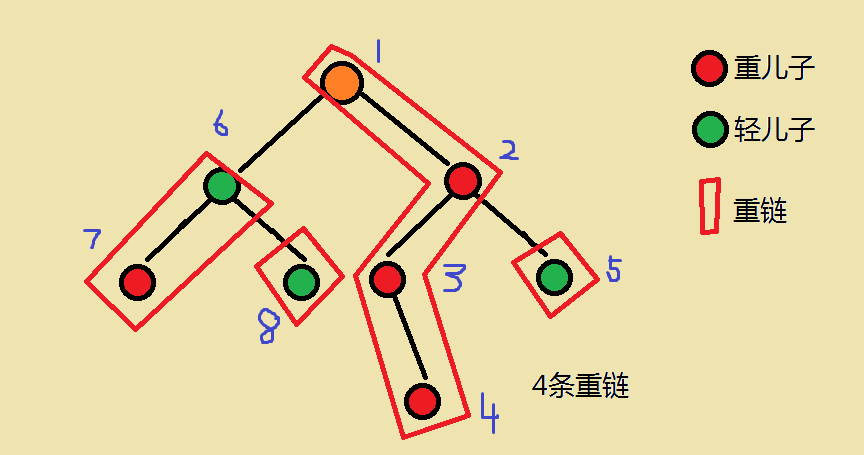
dfs2()过程中,我们需要 优先处理重儿子,这是为了保证 同一条重链 对应的必然是 一段连续的区间。
这样处理以后,我们能得到如下的DFS序编号:
int w[maxn]; //weight
int arr[maxn]; // array for segment tree to use
int top[maxn], id[maxn];
int cnt = 1; //current id
void dfs2(int cur, int t) {
id[cur] = cnt++;
top[cur] = t;
arr[id[cur]] = w[cur];
if (!son[cur]) return; // 这个节点是leaf
dfs2(son[cur], t); // 优先处理重儿子
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[cur] || to == son[cur]) continue; //重儿子处理过了
dfs2(to, to); // 轻儿子是重链的开始
}
}
建线段树
常规操作,并没有什么不同。
将树上操作对应到区间上
操作 $3,4$ (更新/查询一个子树内的值):
在DFS序中,同一个子树内的DFS序编号是连续的,我们有了 parent 对应的编号,就有了区间上的左端点,利用 sz[] 来找到 右端点,左右端点都有了,就用线段树处理即可。
void update_tree(int u, ll x) {
update(1, id[u], id[u]+sz[u]-1, x);
}
ll query_tree(int u) {
return query(1, id[u], id[u]+sz[u]-1);
}
操作 $1,2$ (更新/查询两个点之间最短路径的值):
给定两个点 u,v:
-
如果
u,v在同一条重链上,那么对应的是区间上的一段连续区间(dep较小的那个对应左端点,dep较深的那个对应右端点),直接用线段树即可。 -
否则,比较
top[u]和top[v],如果dep[top[u]] > dep[top[v]](top[u]比top[v]更深),就将u往上跳,在线段树上操作u到top[u]的这一段操作,然后跳到par[top[u]]上(即,重链顶端再往上一格),然后重新执行上述判断。
为什么要让
top更深的来跳?为了保证不会跳过头!
证明:无论怎么跳,我们都不能超过 u,v 的LCA。设 LCA(u,v) = x,因为它们不在同一条链上,那么 u,v 必然在 x 的两边(或者,其中之一刚好等于 x,另外一个被一个轻儿子挡住了)。无论是哪种情况,因为重链有可能直接从 root 一直延伸下来,所以肯定不能选 top 更靠上层的那个。
而选择 top 更深的那个,能够保证我们 最远只能刚好跳到x处(因为 x 有且仅有一个重儿子,如果不跳这个重儿子,必然不会跳出 x 的范围)。
• 由上分析,我们还能发现:在往上跳的过程中,如果发现 u,v 在同一条重链上,那么 dep 较小的那个节点,就是 u,v 的LCA!
void update_path(int u, int v, ll x) {
while (top[u] != top[v]) { // u,v 还不是同一个重链上
if (dep[top[u]] < dep[top[v]]) swap(u,v);
update(1, id[top[u]], id[u], x);
u = par[top[u]]; // 往上跳
}
if (dep[u] > dep[v]) swap(u,v); // dep较小的是左端点
update(1, id[u], id[v], x);
}
ll query_path(int u, int v) {
ll res = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
res = (res + query(1, id[top[u]], id[u])) % mod;
u = par[top[u]];
}
if (dep[u] > dep[v]) swap(u,v);
res = (res + query(1, id[u], id[v])) % mod;
return res;
}
树链剖分变种(询问边)
如果我们把问题稍微改一下:
假如现在不再是点上有权值,而是 边上有权值,修改/询问 $(u,v)$ 之间路径上所有边的权值,怎么处理?
注意到树有一个特别的性质:
每个节点只有 $1$ 个parent。
所以我们可以将 边 转化为 点。
对于一个节点 $u$,如果它有一个parent $p$,那么我们就可以将 $(u,p)$ 这条边,转化为 $u$ 这个点。
对于每次修改/询问 $(u,v)$,先找到 $LCA(u,v) = x$,然后正常更新,最后将 $x$ 的修改/询问全部撤销掉即可。
• 或者,注意到在树链剖分每次 query(u,v) 的最后一个阶段,$u,v$ 中深度较浅的那个是 $LCA(u,v)=x$,所以如果要忽略 $x$ 的影响,我们最后一次 query 的时候可以把线段树上的 index + 1 即可。
例如这样:
void update_path(int u, int v, int x) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
update(1, 1, n, id[top[u]], id[u], x);
u = par[top[u]];
}
if (dep[u] > dep[v]) swap(u,v);
if (id[u] + 1 <= id[v])
update(1, 1, n, id[u]+1, id[v], x); // 给它 + 1
}
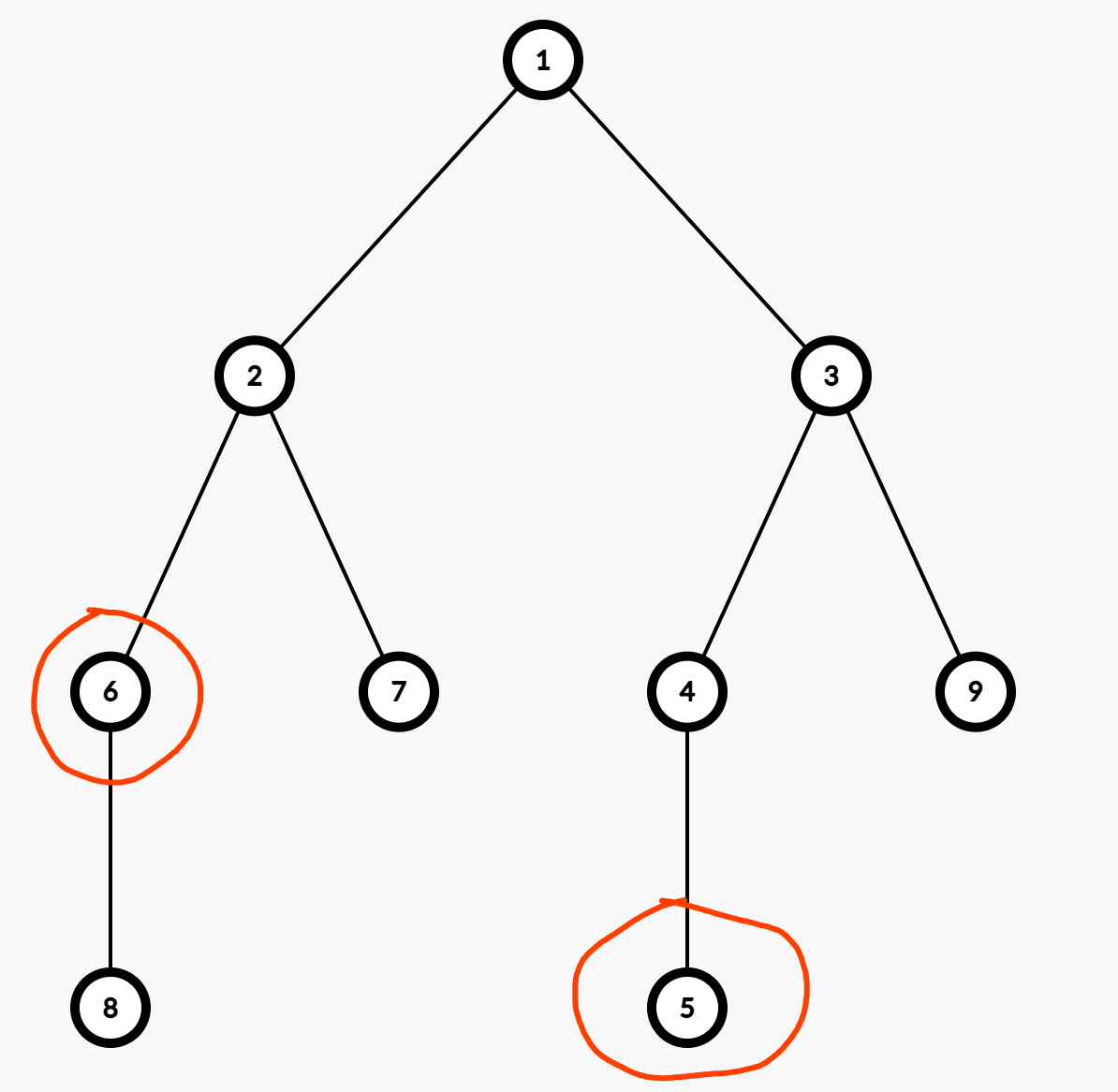
如上图,$(6,2)$ 这个边,就可以用 $6$ 这个点来表示。
修改 $6,5$ 之间的路径,就相当于修改 $[6,2]$ 和 修改 $[5,3]$。
时间复杂度
性质1
如果 $v$ 是 $u$ 的轻儿子,那么 $size(v) \leq \frac{size(u)}{2}$
证明:根据定义即可。
性质2
树中任意两条节点之间,重链的数量 $\leq \log_2(n)$
证明:因为每出现一个重链,意味着出现了一个轻儿子,根据性质1,size减少一半,所以
#重链 $=$ #轻儿子 $= log_2(n)$
由性质1,2,我们可知:
-
路径修改/查询:每个重链进行一次线段树操作,有 $log_2(n)$ 个重链,每次线段树操作复杂度为 $log_2(n)$,所以每次路径操作的总复杂度为 $(log_2(n))^2$
-
子树修改/查询:只有一次线段树操作,所以复杂度为 $log_2(n)$
代码
#define ll long long
const int maxn = 1e5+5;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int n,m,root;
int w[maxn]; //weight
int dep[maxn], par[maxn], sz[maxn], son[maxn];
int top[maxn], id[maxn];
int arr[maxn]; // array for segment tree to use
int cnt = 1; //current id
void dfs1(int cur, int p) {
dep[cur] = dep[p] + 1;
par[cur] = p;
sz[cur] = 1; // 包括自己
int maxsz = -1;
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, cur);
sz[cur] += sz[to];
if (sz[to] > maxsz) { // 更新重儿子
maxsz = sz[to];
son[cur] = to;
}
}
}
void dfs2(int cur, int t) {
id[cur] = cnt++;
top[cur] = t;
arr[id[cur]] = w[cur];
if (!son[cur]) return; // leaf
dfs2(son[cur], t);
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[cur] || to == son[cur]) continue;
dfs2(to, to); // 轻儿子是重链的开始
}
}
struct node {
ll sum = 0;
ll lazy = 0;
} tr[4*maxn];
inline ll len(int cur, int l, int r) {
return r - l + 1;
}
void push_up(int cur) {
tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum;
}
void push_down(int cur) {
if (!tr[cur].lazy) return;
int lc = cur<<1, rc = lc|1;
tr[lc].lazy = tr[lc].lazy + tr[cur].lazy;
tr[rc].lazy = tr[rc].lazy + tr[cur].lazy);
tr[lc].sum = tr[lc].sum + len(lc) * tr[cur].lazy;
tr[rc].sum = tr[rc].sum + len(rc) * tr[cur].lazy;
tr[cur].lazy = 0;
}
void build(int cur, int l, int r) {
if (l == r) {
tr[cur].sum = arr[l];
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
void update(int cur, int l, int r, int L, int R, ll x) {
if (L <= l && r <= R) {
tr[cur].lazy = tr[cur].lazy + x;
tr[cur].sum = tr[cur].sum + x * len(cur);
return;
}
int mid = (l+r) >> 1;
push_down(cur);
if (L <= mid) update(cur<<1, l, mid, L, R, x);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
push_up(cur);
}
ll query(int cur, int l, int r, int L, int R) {
ll res = 0;
if (L <= l && r <= R) {
return tr[cur].sum;
}
int mid = (l+r) >> 1;
push_down(cur);
if (L <= mid) res += query(cur<<1, l, mid, L, R);
if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
push_up(cur);
return res;
}
void update_tree(int u, ll x) {
update(1, id[u], id[u]+sz[u]-1, x);
}
ll query_tree(int u) {
return query(1, id[u], id[u]+sz[u]-1);
}
void update_path(int u, int v, ll x) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
update(1, id[top[u]], id[u], x);
u = par[top[u]];
}
if (dep[u] > dep[v]) swap(u,v);
update(1, id[u], id[v], x);
}
ll query_path(int u, int v) {
ll res = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
res = (res + query(1, 1, n, id[top[u]], id[u])) % mod;
u = par[top[u]];
}
if (dep[u] > dep[v]) swap(u,v);
res = res + query(1, 1, n, id[u], id[v]);
return res;
}
int main() {
cin >> n >> m >> root >> mod;
for (int i = 1; i <= n; i++) cin >> w[i];
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
dfs1(root, 0);
dfs2(root, root);
build(1, 1, n);
while (m--) {
int op; cin >> op;
if (op == 1) {
int u,v,x;
cin >> u >> v >> x;
update_path(u,v,x);
} else if (op == 2) {
int u,v; cin >> u >> v;
ll res = query_path(u,v);
cout << res << "\n";
} else if (op == 3) {
int u,x; cin >> u >> x;
update_tree(u, x);
} else {
int u; cin >> u;
ll res = query_tree(u);
cout << res << "\n";
}
}
}
例题
例1 洛谷P2486 [SDOI2011]染色
题意
给定 $n$ 个节点的树,每个节点都有一个初始的颜色 $c_i$。
有 $m$ 个操作,操作共两种:
$C ~ a ~ b ~ c$:将 $a$ 到 $b$ 的路径上的所有节点染色为 $c$。
$Q ~ a ~ b$:输出 $a$ 到 $b$ 的路径上的颜色段数量。
• 颜色段的定义:每个最长的同颜色的连续子序列,叫做一个颜色段。例如 $[2,1,1,2,2,1]$ 具有 $4$ 个颜色段。
题解
比较明显的树剖思路。问题在于如何维护颜色段的数量?
先思考一下在一个 数组 上,如何维护?
如果两个相邻的区间,相邻的部分的颜色相同,那么它们将合并为一个颜色段。
所以,对于每一个区间,我们维护它 左端点的颜色 和 右端点的颜色,并且维护 区间内颜色段的数量。
在 push_up() 的时候,记得检查一下左区间的右端点 和 右区间的左端点颜色是否相同即可。
那么如何在树上进行查询?
需要注意的是 在树剖中,查询的不一定是数组上的连续区间,但是在树上是连续的。
所以每次查询完一段区间 $[top[u], u]$,要记录这段区间的左端点 $top[u]$ 的颜色。
继续往上跳的时候,下一段区间的右端点是 $par[top[u]]$。
所以要比较一下 $top[u]$ 和 $par[top[u]]$ 的颜色是否相同。相同的话,把答案减 $1$。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
struct node {
int l,r;
int lc, rc, cnt; //left color, right color
bool lazy = 0;
} tr[maxn<<2];
int color[maxn], last, ori[maxn], par[maxn]; // ori[u] 代表u的颜色
int n,m;
void push_up(int cur) {
int l = cur<<1, r = cur<<1|1;
tr[cur].cnt = tr[l].cnt + tr[r].cnt;
tr[cur].lc = tr[l].lc, tr[cur].rc = tr[r].rc;
if (tr[l].rc == tr[r].lc) tr[cur].cnt--; // 合并颜色段
}
void push_down(int cur) {
if (!tr[cur].lazy) return;
int l = cur<<1, r = cur<<1|1;
tr[cur].lazy = 0;
tr[l].cnt = tr[r].cnt = 1;
tr[l].lazy = tr[r].lazy = 1;
int c = tr[cur].lc;
tr[l].lc = tr[r].lc = tr[l].rc = tr[r].rc = c;
}
void build(int cur, int l, int r) {
tr[cur].l = l, tr[cur].r = r;
if (l == r) {
tr[cur].cnt = 1;
tr[cur].lc = tr[cur].rc = color[l];
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
void update(int cur, int l, int r, int L, int R, int c) {
if (l >= L && r <= R) {
tr[cur].cnt = 1;
tr[cur].lc = tr[cur].rc = c;
tr[cur].lazy = 1;
return;
}
push_down(cur);
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, c);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, c);
push_up(cur);
}
int query(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) {
return tr[cur].cnt;
}
push_down(cur);
int mid = (l+r) >> 1;
int res = 0;
if (L <= mid) res += query(cur<<1, l, mid, L, R);
if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
if (L <= mid && R > mid && tr[cur<<1].rc == tr[cur<<1|1].lc) res--; // 合并颜色段
return res;
}
int head[maxn], ecnt = 1, son[maxn], id[maxn], idcnt = 0, top[maxn], sz[maxn], dep[maxn];
struct Edge {
int to,nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
void dfs(int u, int p) {
sz[u] = 1;
par[u] = p;
dep[u] = dep[p] + 1;
int maxsz = -1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
sz[u] += sz[to];
if (sz[to] > maxsz) son[u] = to, maxsz = sz[to];
}
}
void dfs2(int u, int p, int topf) {
id[u] = ++idcnt;
color[idcnt] = ori[u];
top[u] = topf;
if (son[u]) dfs2(son[u], u, topf);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p || to == son[u]) continue;
dfs2(to, u, to);
}
}
void update(int u, int v, int c) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
int p = top[u];
int L = id[p], R = id[u];
update(1, 1, n, L, R, c);
u = par[p];
}
if (dep[u] > dep[v]) swap(u,v);
update(1, 1, n, id[u], id[v], c);
}
int query_color(int cur, int l, int r, int p) {
if (l == r) return tr[cur].lc;
push_down(cur);
int mid = (l+r) >> 1;
if (p <= mid) return query_color(cur<<1, l, mid, p);
else return query_color(cur<<1|1, mid+1, r, p);
}
void query(int u, int v) {
int ans = 0;
int lastu = -1, lastv = -1; // u和v 的上一次查询的左端点
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v), swap(lastu, lastv);
int p = top[u];
int L = id[p], R = id[u];
ans += query(1, 1, n, L, R);
if (lastu == query_color(1, 1, n, R)) { // 如果上一次查询的左端点,等于这次查询的右端点
ans--;
}
lastu = query_color(1, 1, n, L); // u和v 的上一次查询的左端点
u = par[p];
}
if (dep[u] > dep[v]) swap(u,v), swap(lastu, lastv);
ans += query(1, 1, n, id[u], id[v]);
if (lastv == query_color(1, 1, n, id[v])) ans--;
if (lastu == query_color(1, 1, n, id[u])) ans--;
cout << ans << "\n";
}
int main() {
fastio;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> ori[i];
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
dfs(1, 0);
dfs2(1, 0, 1);
build(1, 1, n);
while (m--) {
char op;
int u,v; cin >> op >> u >> v;
if (op == 'Q') {
query(u,v);
} else {
int c; cin >> c;
update(u,v,c);
}
}
}
