数位DP

• 因为不推荐这么写，所以折叠了。

本质和记忆化搜索相同，DP速度可能较快，但是一般很难写，一般有两种写法：

写法一：

令 dp 数组记录 严格小于数字 $x$ 的满足条件的数量。

将数位按照 高位到低位 排好，然后对于前缀等于 $x$ 的那些数，进行单独处理。

这种写法可以见 ABC194F的题解

写法二：

将数位按照 低位到高位 排好。（注意，和上面相反）

预处理出 dp 数组（不带任何限制）。

预处理以后，对于每一个询问，都直接进行处理，有3种情况：

(以下的 $n$ 指的是当前询问数字 $x$ 的数位个数)

1. 数字使用的位数 $< n$，则没有任何限制，直接加上即可。
2. 数字使用的位数 $= n$，且最高位的数字 $< arr[n]$，也没有任何限制，直接加上即可。
3. 数字使用的位数 $= n$，且最高位的数字 $= arr[n]$，则我们需要从最高位的前一位 n-1 开始，对于每一位 i，都枚举当前使用的数字 j = 0,1,...,arr[i]-1，然后再到前一位 i-1。

为什么不枚举 j = arr[i] 的情况？

注意到 dp 数组里表示的是不带任何限制的数量，当 j = arr[i] 时，更高位的数字都被固定为 $x$ 的高位部分了，所以是有限制的，不能算进去。

以下给出 SCOI2009 windy 数 的写法：

ll dp[12][12];
int arr[12];

void init() {  // 处理无限制的部分
    for (int j = 0; j <= 9; j++) dp[1][j] = 1;
    for (int i = 2; i <= 11; i++) {
        for (int j = 0; j <= 9; j++) {
            for (int k = 0; k <= 9; k++) {
                if (abs(j-k) < 2) continue;
                dp[i][j] += dp[i-1][k];
            }
        }
    }
}

ll solve(int a) {
    if (!a) return 0;
    p = 0;
    while (a) {
        arr[++p] = a % 10;
        a /= 10;
    }
    ll ans = 0;
    for (int i = 1; i <= p-1; i++) {
        for (int j = 1; j <= 9; j++) ans += dp[i][j];  // Case1: 位数 < p
    }

    for (int j = 1; j < arr[p]; j++) ans += dp[p][j];  // Case2: 位数 = p，最高位 < p

    for (int i = p-1; i >= 1; i--) {  // Case3: 位数 = p，最高位 == arr[p]
        for (int j = 0; j <= arr[i]-1; j++) {  // 枚举第i位 < arr[i]的情况 (等于的情况需要单独来处理)
            if (abs(j - arr[i+1]) < 2) continue;
            ans += dp[i][j];
        }
        // 第i位 == arr[i] 时, 如果高位固定的部分已经不满足了，就不用看后面了
        if (abs(arr[i] - arr[i+1]) < 2) break;
    }
    if (check()) ans++;  // 检查一下这个数字 arr[] 本身是否满足条件
    return ans;
}

注：在DP处理高位 等于 $x$的高位 时，一定要注意 高位的数字都已经被固定了，所以需要算进答案里，或者需要检查一下被固定的数是否满足条件了。

注：最后要单独检查一下 这个数字 $x$ 本身是否满足条件。

#include <bits/stdc++.h>
using namespace std;
ll dp[12][12];
int arr[12];

void init() {
    for (int j = 0; j <= 9; j++) dp[1][j] = 1;

    for (int i = 2; i <= 11; i++) {
        for (int j = 0; j <= 9; j++) {
            for (int k = 0; k <= 9; k++) {
                if (abs(j-k) < 2) continue;
                dp[i][j] += dp[i-1][k];
            }
        }
    }
}

int p;
bool check() {
    for (int i = 2; i <= p; i++) {
        if (abs(arr[i] - arr[i-1]) < 2) return 0;
    }
    return 1;
}
ll solve(int a) {
    if (!a) return 0;
    p = 0;
    while (a) {
        arr[++p] = a % 10;
        a /= 10;
    }
    ll ans = 0;
    for (int i = 1; i <= p-1; i++) {
        for (int j = 1; j <= 9; j++) ans += dp[i][j];  // Case1: 位数 < p
    }

    for (int j = 1; j < arr[p]; j++) ans += dp[p][j];  // Case2: 位数=p，最高位 < p

    for (int i = p-1; i >= 1; i--) {  // Case3: 位数=p，最高位=p
        for (int j = 0; j <= arr[i]-1; j++) {  // 枚举第i位 < arr[i]的情况 (等于的情况需要单独来处理)
            if (abs(j - arr[i+1]) < 2) continue;
            ans += dp[i][j];
        }
        // 第i位 == arr[i] 时, 如果前缀已经不满足了，就不用看后面了
        if (abs(arr[i] - arr[i+1]) < 2) break;
    }
    if (check()) ans++;
    return ans;
}

int main() {
    init();
    int a,b; cin >> b >> a;
    int r = solve(a) - solve(b-1);
    cout << r << endl;
}

我们枚举每一个digit，然后进行记忆化搜索即可。

记忆化搜索一般比较模版化，其中 zero, limit 的套路是可以背下来的。

对于本题，枚举每一个digit $cur$，令 $dp[i][j]$ 表示到了 第 $i$ 位，包含 $j$ 个 $cur$的数字数量。

#include <bits/stdc++.h>
using namespace std;
ll a,b;
ll dp[14][14];  // dp[i][j]: 到第i位，包含j个cur的数的数量

int arr[14];  // 数字x的各个数位 （从低位到高位）
int n;  // 数字x的长度
int cur;  // 当前枚举的数字 (0...9)

// pos: 当前到了第几位
// cnt: 当前数字包含了 cnt 个 cur
// zero: 是否有前缀 0
// limit: 前面部分是否完全等于高位
ll dfs(int pos, int cnt, bool zero, bool limit) {
    if (pos <= 0) {
        return cnt;
    }
    if (!zero && !limit && dp[pos][cnt] != -1)  // 只有在 (!zero && !limit) 时获得dp值，否则继续往下搜索
        return dp[pos][cnt];  
    int ed = 9;
    if (limit) ed = arr[pos];  // 如果前面完全等于高位，那么这一位不能超过当前位

    ll res = 0;
    for (int j = 0; j <= ed; j++) {
        if (!j && zero) res += dfs(pos-1, 0, 1, 0);  // 如果仍然保持前缀 0，那么记得将 cnt 清零，limit也要清零。
        else {
            res += dfs(pos-1, cnt + (j == cur), 0, limit && (j == arr[pos]));
        }
    }
    if (!zero && !limit) dp[pos][cnt] = res;  // 只有在 (!zero && !limit) 时记录dp值
    return res;
}

ll solve(ll x) {
    n = 0;
    memset(dp, -1, sizeof(dp));
    while (x) {
        arr[++n] = x % 10;
        x /= 10;
    }
    return dfs(n, 0, 1, 1);  // 从高位开始
}

int main() {
    cin >> a >> b;
    for (cur = 0; cur <= 9; cur++) {
        cout << solve(b) - solve(a-1) << " ";
    }
    cout << endl;
}

我们只需要考虑长度为 $2$ 或者 $3$ 的回文子串即可（因为 $>3$ 的情况已经被它们两个包含了）。

那么我们可以设定 dp 数组为：

$dp[i][j][k][0/1]$：我们当前在第 $i$ 位，往前 $2$ 位的数字为 $j$，往前 $1$ 位的数字为 $k$，且 不包含（0）/ 包含（1） 回文子串 的数字数量。

注意到，最后一维度判断了是否包含回文子串。因为一个数有可能 前面几位没有回文子串，但是 后来又有了。如果我们只记录 包含 的情况，会漏掉很多答案。

而 dfs() 函数的意思是：我们从当前这个状态出发，能获得多少符合条件的数字。

注：有的时候，前 $1$ 位，前 $2$ 位上可能没有数字，我们可以设定这些空着的位为 $10$。

注：因为本题数字过大，所以不采用减去 $dfs(L-1)$ 的形式，而是 减去 $dfs(L)$，然后特判一下 $L$ 本身是否满足。

#include <bits/stdc++.h>
using namespace std;

ll dp[1002][11][11][2]; 
string s;
int n;

ll dfs(int pos, int pre2, int pre1, bool zero, bool limit, bool moe) {
    if (pos >= n) {
        return moe;
    }
    int ed = 9;
    if (limit) ed = s[pos] - '0';
    if (!limit && !zero && dp[pos][pre2][pre1][moe] != -1) return dp[pos][pre2][pre1][moe];

    ll res = 0;
    for (int j = 0; j <= ed; j++) {
        if (!j && zero) (res += dfs(pos+1, 10, 10, 1, 0, 0)) %= mod;
        else {
            (res += dfs(pos+1, pre1, j, 0, limit && (j == ed), moe || (j == pre1 || j == pre2))) %= mod;
        }
    }
    if (!limit && !zero) dp[pos][pre2][pre1][moe] = res;
    return res;
}

ll solve(string a) {
    n = a.size();
    if (n <= 1) return 0;
    memset(dp, -1, sizeof(dp));
    s = a;
    return dfs(0, 10, 10, 1, 1, 0);
}

bool check(string s) {
    int n = s.size();
    for (int i = 0; i < n-1; i++) {
        if (s[i] == s[i+1]) return 1;
        if (i+2 < n && s[i] == s[i+2]) return 1;
    }
    return 0;
}

int main() {
    string a,b;
    cin >> a >> b;
    ll r = solve(b) - solve(a);
    r += check(a);
    cout << (r % mod + mod) % mod << endl;
}

可以发现最大的数字只有 $18$ 个 $9$，所以最大的数位和就是 $18 \times 9 = 162$。

所以我们可以枚举数位和 $cur$，然后找到符合以下条件的数字 $x$ 的数量：

1. $x \in [a,b]$
2. $x$ 各位置上数位和 等于 $cur$
3. $x \text{ mod } cur = 0$

令 dp 数组为：

$dp[i][j][k]$：当前到了第 $i$ 位，数位和为 $j$，数字本身 $\text{mod } cur = k$ 的数字数量。

注意到本题不关心前缀 $0$，因为就算有前缀 $0$，也不会对 dfs() 内的其他参数 $sum, v$ 产生任何影响，也不会对枚举当前位使用的数字 $j$ 产生影响，所以可以舍去了。

有一个很重要的优化（在多testcase的情况下，优化程度极大）：

注意到代码里面：

for (cur = 1; cur <= 162; cur++) {
    memset(dp, -1, sizeof(dp));
    ans += solve(b) - solve(a-1);
}

我们在 solve(b) 结束后，并没有 memset(dp, -1, sizeof(dp));

这是因为我们的 dfs() 是从高位开始，枚举到低位。因为 dp[] 数组里保存的都是 !limit 的无限制情况，所以这里面的内容是可以重复利用的！

但是对于 不同的 cur 就不能重复利用了，因为数组本身的意义已经不同了。

#include <bits/stdc++.h>
using namespace std;

ll dp[19][163][163];
int arr[19];
int n;
int cur;

ll dfs(int pos, int sum, int v, bool limit) {  // sum为数位和，v为 x % cur 的值
    if (!pos) {
        return (sum == cur) && (!v);
    }
    if (!limit && dp[pos][sum][v] != -1) return dp[pos][sum][v];
    int ed = 9;
    if (limit) ed = arr[pos];

    ll res = 0;
    for (int j = 0; j <= ed; j++) {
        res += dfs(pos-1, sum + j, (v * 10 + j) % cur, limit && (j == ed));
    }
    if (!limit) dp[pos][sum][v] = res;
    return res;
}

ll solve(ll x) {
    n = 0;
    while (x) {
        arr[++n] = x % 10;
        x /= 10;
    }
    return dfs(n, 0, 0, 1);
}

int main() {
    memset(dp, -1, sizeof(dp));
    ll a,b; cin >> a >> b;
    ll ans = 0;
    for (cur = 1; cur <= 162; cur++) {
        memset(dp, -1, sizeof(dp));
        ans += solve(b) - solve(a-1);
    }
    cout << ans << endl;
}

$x$ 可以被每一位上的数字整除 $\iff$ $x \text { mod } lcm = 0$

其中 $lcm$ 是 $x$ 每一位上的数字的 $lcm$。

发现 $lcm(1,2,…,9) = 2520$，所以我们可以大致得出以下的状态：

$dp[i][j][k]$：我们来到了第 $i$ 位，$j$ 表示我们使用了哪些数字，$k$ 代表当前数字 $x \text { mod } 2520$ 的值。

这样最后在 pos == 0 时，判断一下 $j$ 对应的 $lcm$，然后判断 $k \text { mod } lcm_j = 0$ 是否成立即可。

现在问题是，这个 $j$ 怎么表示？（$j$ 代表 $x$ 用了 $0,1,2,…9$ 中的哪些数字）

可以用状压来实现，其中忽略掉 $0,1$，只记录是否包含 $2,3,…,9$。大概有 $2^8 - 1$ 种状态，但是这样仍然会 $TLE$，怎么办？

我们发现，记录使用了哪些数字，只是为了求出这些数字的 $lcm$，那我们直接记录 $lcm$ 作为状态即可！

但是好像维度反而变大了，因为 $lcm$ 最大可以达到 $2520$，比之前状压的 $2^8 - 1$ 还大。

再观察一下，发现我们只关心有效的 $lcm$ 值，$2520$ 内的绝大多数值是无效的，所以我们可以枚举出所有 有效的 $lcm$，而这些有效的 $lcm$ 就是 $2520$ 的所有因子。总共只有 $48$ 个。

所以我们只需要进行一次 离散化 的操作，将这些因子 map 到 $0,1,2,…,47$，这样 $j$ 就可以只用 $48$ 个数字来表示了。

最后就是 memset(dp, -1, sizeof(dp)) 的优化了，因为本题的 dp[] 数组在不同的 case 之间的含义没有任何变化（都是 $\text {mod } 2520$），所以只在一开始 memset 一次，之后就一直重复利用。

• 本题的 memset 优化非常重要，因为有 $T = 10$ 个 case ，大概会有 $2 \times T = 20$ 倍左右的速度差（如果不优化会 $TLE$ 的很惨）。

#include <bits/stdc++.h>
using namespace std;
const int mod = 2520;

ll dp[20][49][2520];
int idx[2521];
int n = 0, arr[20];

int gcd(int a, int b) {
    if (!b) return a;
    return gcd(b, a%b);
}

int LCM(int a, int b) {
    return a/gcd(a,b)*b;
}

vector<int> fac;
void init() {
    for (int i = 1; i <= sqrt(mod); i++) {
        if (mod % i == 0) {
            fac.push_back(i);
            if (i != mod/i) fac.push_back(mod/i);
        }
    }
    sort(fac.begin(), fac.end());
    for (int i = 0; i < fac.size(); i++) {
        idx[fac[i]] = i;  // 离散化，例如 idx[1] = 0, idx[2520] = 47
    }
}

// lc 代表当前的 lcm, v 代表 x % 2520 的值
ll dfs(int pos, int lc, int v, bool limit) {
    if (pos <= 0) {
        return v % lc == 0;  // 注意，只有在 pos == 0时，才判断 % lc，其余情况都是 % 2520
    }

    if (!limit && dp[pos][idx[lc]][v] != -1) 
        return dp[pos][idx[lc]][v];

    int ed = 9;
    if (limit) ed = arr[pos];
    ll res = 0;
    for (int j = 0; j <= ed; j++) {
        int newval = (v * 10 + j) % mod;
        if (j < 2) res += dfs(pos-1, lc, newval, limit && (j == ed));
        else res += dfs(pos-1, lcm(lc, j), newval, limit && (j == ed));
    }

    if (!limit) dp[pos][idx[lc]][v] = res;
    return res;
}

ll solve(ll x) {
    n = 0;
    while (x) {
        arr[++n] = x % 10;
        x /= 10;
    }
    return dfs(n,1,0,1);
}

int main() {
    init();
    int T; cin >> T;
    memset(dp, -1, sizeof(dp));  // 注意，只进行一次 memset
    while (T--) {
        ll l,r; cin >> l >> r;
        l--;
        cout << solve(r) - solve(l) << endl;
    }
}

$dp[i][j][k]$：使用到 $i$ 位，每一位的和 $\text{mod } 7 = j$，数字本身 $\text{mod } 7 = k$ 的平方和。

将返回值设定为该数字的平方，然后将 dp 数组的值作为平方之和。

为什么是错的？

考虑记忆化状态：

那么，数字 $10,80$ 的状态完全相同，但是因为我们先 dfs 到了 $10$，然后到了 $80$ 的时候就会直接返回，没有计算 $80^2$ 的值，导致答案错误。

注意这个题和其他例题完全不一样，因为其他题求的都是 数字的数量，而只有这个题求的是 平方之和。

这直接导致，我们在状态转移的时候 不能简单的相加。

上面做法的 dp 状态没有问题：

$dp[i][j][k]$：使用到 $i$ 位，每一位的和 $\text{mod } 7 = j$，数字本身 $\text{mod } 7 = k$

但是 dp[] 数组对应的值，不能简单的设定为平方和。

如果这个题求的是满足条件的数字数量，是不是就可以了？

是的！比如 $2$ 和 $9$ 对应的状态相同，无论后缀是什么，只要满足条件，它们就完全等价。

比如后缀是数字 $3$，那么 $23, 93$ 就完全等价，所以我们来到前缀 $9$ 的时候就可以直接利用前缀 $2$ 的信息。

但是在本题中，$23$ 和 $93$ 并不等价，因为 $23^2 \neq 93^2$。

所以我们要考虑一下组合数学/计数题中的 贡献 套路。

我们在 dfs 过程中，先算出来了前缀 $2$ 的相关信息。我们假设前缀 $2$ 有着 三个有效的后缀 $2,3,4$，那么数字就是 $22,23,24$。

此时，我们已经算出了这些后缀的相关信息，怎么把它合并上去？

$$22^2 + 23 ^ 2 + 24^2 = (20+2)^2 + (20+3)^2 + (20+4)^2$$ $$= 3\times 20^2 + 2 \times 20 \times (2+3+4) + (2^2+3^2+4^2)$$

如果这里还不太清楚，还可以再举一个例子：

我们有一个前缀 $1$，后缀是 $21,22$，那么合并的过程就是：

$$121^2+122^2 = (100+21)^2 + (100+22)^2 $$ $$=2 \times 100^2 + 2 \times 100 \times (21+22) + (21^2+22^2)$$

更 General 的写法是，给定一个digit $a$（$a$ 实际上就是 dfs() 过程中，当前使用的数字），然后假设我们有 $n$ 个后缀 $b_1,b_2,…,b_n$，那么：

$$(ab_1)^2 + (ab_2)^2 + … + (ab_n)^2 = (a \times 10^p + b_1) ^ 2 + (a \times 10^p + b_2) ^ 2 + …+(a \times 10^p + b_n) ^ 2$$

$$= n \times a^2 \times 10^{2p} + 2\times10^p \times (b_1+b_2+…+b_n) + (b_1^2+b_2^2+…+b_n^2)$$

$$= \sum\limits_{i=1}^n ((a^2\times 10^{2p}) + (2\times10^p\times b_i) + (b_i^2))$$

• 其中，$p$ 就是 $pos-1$

但是注意到，$b_i$ 是一个后缀，它代表的是 dp[] 数组里面，pos-1 的部分，所以它本身也是一个贡献（它并不是一个数字）。

比如上面的第二个例子中，前缀为 $1$，后缀 $b_1$ 实际上是 $2$，这个 $b_1$ 有两个后缀 $2,3$，所以 $c_1 = 2, c_2 = 3$

那么，我们单独看一下每一个 $b$ 带来的贡献是多少。

对于某一个后缀 $b$，我们继续考虑它的后缀 $c_j$，$b$ 带给 前缀 $a$ 的贡献可以这么表示：

$$\sum\limits_{j=1}^m ((a^2\times 10^{2p}) + (2\times10^p\times c_j) + (c_j^2))$$

$$=m\times a^2\times 10^{2p} + (2\times 10^p \times \sum\limits_{j=1}^mc_j) + (\sum\limits_{j=1}^m c_j^2)$$

其中，$m$ 是 $b$ 的 后缀数量，$\sum\limits_{j=1}^mc_j$ 是 $b$ 的后缀的值之和， $\sum\limits_{j=1}^m c_j^2$ 是 $b$ 的后缀的平方和。

由上，我们可以看出，对于每一个后缀 $b$，我们都要维护它的

1. 后缀 数量 $cnt$
2. 后缀值 之和 $sum_1$
3. 后缀值的 平方和 $sum_2$

则，这个 $b$ 带给 $a$ 的 平方和 的贡献就是：

$$\sum ((a^2\times 10^{2p}) + (2\times10^p\times c_j) + (c_j^2))$$

$$= (\sum a^2\times 10^{2p}) + (2\times10^p\times \sum c_j) + \sum c_j^2$$

$$ = cnt \times (a^2\times 10^{2p}) + (2\times10^p\times sum_1) + (sum_2)$$

那么 $b$ 带给 $a$ 的 后缀和 的贡献呢？

$$a \times 10^p + b$$

$$= \sum (a \times 10^p) + \sum c_j$$

$$= (cnt \times a \times 10^p) + sum_1$$

那么 $b$ 带给 $a$ 的 后缀数量 的贡献呢？

$$1= \sum_j 1 = cnt$$

下面会给一个并不严谨，但是比较好理解的公式推导。

注：实现过程中，我们用 struct node 来维护这些信息。

平方和：

$$(a \times 10^p + b)^2$$

$$= (a^2\times 10^{2p}) + (2\times10^p) \times b + (b^2)$$

然后对其进行求和操作，有：

$$\sum (a^2\times 10^{2p}) + (2\times10^p) \times \sum b + \sum b^2$$

$$= cnt \times (a^2\times 10^{2p}) + (2\times10^p\times sum_1) + (sum_2)$$

值的和：

$$(a \times 10^p + b)$$

对其进行求和操作：

$$\sum a\times10^p + \sum b$$

$$=cnt \times a \times 10^p + sum_1$$

数量之和：

$$1$$

对其进行求和：

$$\sum 1$$

$$=cnt$$

#include <bits/stdc++.h>
using namespace std;

struct node {
    ll cnt, sum1, sum2;
};

ll pow10[20];
node dp[20][7][7];
bool vis[20][7][7];
int n, arr[20];
node dfs(int pos, int sum, int md, bool limit) {
    if (!pos) {
        if (!md) return {0,0,0};
        if (!sum) return {0,0,0};
        return {1,0,0};  // 注意这里是 {1,0,0}，因为没有选择任何值
    }
    if (!limit && vis[pos][sum][md]) {
        return dp[pos][sum][md];
    }
    ll cnt = 0, sum1 = 0, sum2 = 0;
    int ed = 9;
    if (limit) ed = arr[pos];
    for (ll j = 0; j <= ed; j++) {
        if (j == 7) continue;

        node res = dfs(pos-1, (sum+j) % 7, (md*10+j) % 7, limit && (j==ed));
        ll c = res.cnt, s1 = res.sum1, s2 = res.sum2;

        cnt = (cnt + c) % mod;

        sum1 = (sum1 + j * pow10[pos-1] % mod * c % mod + s1) % mod;

        sum2 = (sum2 + j * j * pow10[pos-1] % mod * pow10[pos-1] % mod * c % mod) % mod;
        sum2 = (sum2 + 2LL * j * pow10[pos-1] % mod * s1 % mod) % mod;
        sum2 = (sum2 + s2) % mod;
    }
    if (!limit) {
        vis[pos][sum][md] = 1;
        dp[pos][sum][md] = {cnt, sum1, sum2};
    }
    
    return {cnt, sum1, sum2};
}

node solve(ll x) {
    n = 0;
    while (x) {
        arr[++n] = x % 10;
        x /= 10;
    }
    return dfs(n, 0, 0, 1);
}

int main() {
    memset(vis, 0, sizeof(vis));
    pow10[0] = 1LL;
    for (int i = 1; i <= 19; i++) pow10[i] = pow10[i-1] * 10LL % mod;
    int T; cin >> T;

    while (T--) {
        ll l,r; cin >> l >> r;
        ll ans = solve(r).sum2 - solve(l-1).sum2;  // 如果是求值的和，改成 sum1 即可
        ans = (ans + (ll)(mod)) % mod;
        cout << ans << endl;
    }
}

和例6是一样的做法，更简单了一些。

回顾一下状态转移：

如果当前 digit 为 $a$，后缀为 $b$，则 $b$ 给 $a_{sum}$ 带来的贡献为：

$$\sum_{i=1}^{cnt} (a * 10^p + b_i) = cnt * a * 10^p + b_{sum}$$

而 $a_{sum}$ 就等于所有后缀 $b$ 的贡献之和。

状态比较容易想：

dp[i][mask] 代表到了第 $i$ 个字符，当前使用的digit组成了 $mask$，dp 的值就是 {cnt, sum}。

• 这里需要注意，在写 dfs() 函数时要考虑是否有前导 $0$。因为如果有前导 $0$，这个 $mask$ 不应包含前导 $0$。

#include <bits/stdc++.h>
using namespace std;

const int mod = 998244353;
const int maxn = 4e5+5;

int K;
int a[20], n;
struct node {
    ll cnt, sum;
};
node dp[20][(1<<10)+5];
bool vis[20][(1<<10)+5];
inline int popcount(int mask) {
    int res = 0;
    while (mask) {
        res += (mask & 1);
        mask >>= 1;
    }
    return res;
}

ll ten[20];
node dfs(int i, int mask, bool zero, bool limit) {
    if (i <= 0) return {1, 0};
    if (!limit && vis[i][mask]) return dp[i][mask];
    ll cnt = 0, sum = 0;
    int ed = (limit ? a[i] : 9);
    for (ll j = 0; j <= ed; j++) {
        if (popcount(mask | (1<<j)) <= K) {
            int newmask = mask | (1<<j);
            if (zero && (!j)) newmask = 0;
            node res = dfs(i-1, newmask, zero && (!j), limit && (j == ed));
            cnt += res.cnt, cnt %= mod;
            sum = ((res.sum + (ten[i-1] * res.cnt % mod * j % mod)) % mod + sum) % mod;
        }
    }
    if (!limit) vis[i][mask] = 1, dp[i][mask] = {cnt, sum};
    return {cnt, sum};
}

ll solve(ll x) {
    n = 0;
    memset(a, 0, sizeof(a));
    memset(dp, 0, sizeof(dp));
    memset(vis, 0, sizeof(vis));
    while (x) {
        a[++n] = x % 10;
        x /= 10;
    }
    return dfs(n, 0, 1, 1).sum;
}

int main() {
    fastio;
    ll L,R;
    cin >> L >> R >> K;
    ten[0] = 1;
    for (int i = 1; i <= 19; i++) ten[i] = ten[i-1] * 10LL % mod;
    ll ans = (solve(R) - solve(L-1) + mod) % mod;
    cout << ans << endl;
}

以前的数位dp都只针对一个数。

而这次的数位dp需要考虑 $k$ 个数，所以比起一个数的情况，记录一个 bool limit 代表是否碰到上限 $m$，我们这次记录一个 $j$ 代表有 $j$ 个数顶到了 $m$ 的上限。

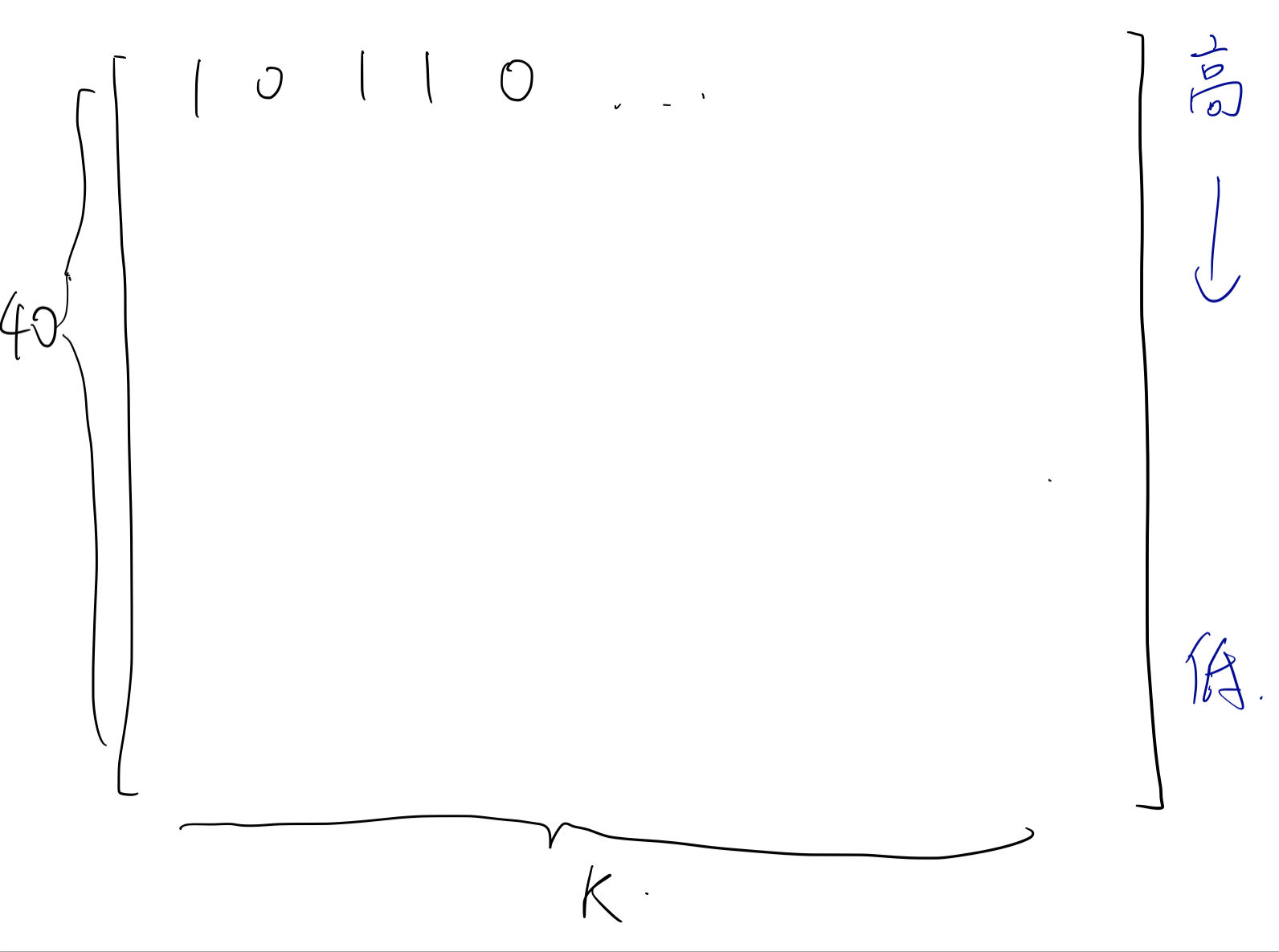
如图，每一列代表一个 $a_i$，而每一行就是每一个 $a_i$ 的每一位上的bit。

注意到我们只关心每一行有几个 $1$ 几个 $0$，这样贡献就可以计算出来。

我们要求：

1. 所有行的贡献之和 $=n$。
2. 每一列不能超过 $m$。

所以我们设计数位dp的状态就是：

dp[i][j][k]：代表到了第 $i$ 位（从高位到低位），有 $j$ 个数顶到了 $m$ 的上限。

而 $k$ 就代表到当前位的贡献和。但 $k$ 可能会非常大，所以我们需要剪枝。

注意到我们可以令 $k$ 等于 $\frac{n-sum}{2^i}$，其中 $sum$ 为之前的贡献之和，这样我们规定 $k \leq 81$ 即可，因为如果 $k > 81$ 那么后面每一行就算贡献最大也不可能使得 $f(A) = n$ 了。

• 实际操作的时候保险一点设定 $k \leq 200$。

• 注意到在数位 dp 中，我们不一定要找出这个数 $m$ 有多少位，直接假设它位数最大（本题中为 $40$）开始处理也可以的。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 70;
 
const int M = 200;
int sm[maxn], sn[maxn];
Z dp[43][20][M+5];
Z C[105][105];
ll n, m, len;  // len: length
 
// i: 从高到低第几位
// j: 有几个数来到了m的上限
// k: (n - 前面贡献的和) / 2^(40-i), 如果 k > M 则不行
Z dfs(int i, int j, int k) {
    if (i <= 0) {
        return k == 0;
    }
    if (dp[i][j][k].val() != -1) return dp[i][j][k];
    Z res = 0;
    if (sm[i] == 0) {  // 这 j 个数只能选 0
        for (int a = 0; a <= len - j; a++) {  // 剩下 K - j 个数里面，有 a 个选 1
            int new_k = k * 2 - a * (len - a) + sn[i];
            if (new_k <= M && new_k >= 0) {
                res = res + C[len-j][a] * dfs(i-1, j, new_k);
            }
        }
    } else {
        for (int a = 0; a <= len - j; a++) {   // a 个 1
            for (int b = 0; b <= j; b++) {   // b 个 1 (到了上限)
                int new_k = k * 2 - (a + b) * (len - a - b) + sn[i];
                if (new_k <= M && new_k >= 0) {
                    res = res + C[len-j][a] * C[j][b] * dfs(i-1, b, new_k);
                }
            }
        }
    }
    
    return dp[i][j][k] = res;
}
 
 
int main() {
    cin >> n >> m >> len;
    memset(dp, -1, sizeof(dp));
 
    C[0][0] = 1;
    for (int i = 1; i <= 100; i++) {
        C[i][0] = 1;
        for (int j = 1; j <= i; j++) {
            C[i][j] = C[i-1][j-1] + C[i-1][j];
        }
    }
 
    if ((n >> 40) > M) {
        cout << 0 << endl;
        return 0;
    }
 
    int id = 0;
    ll tn = n;
    while (tn) {
        sn[++id] = (tn & 1);
        tn >>= 1;
    }
 
    id = 0;
    ll tm = m;
    while (tm) {
        sm[++id] = (tm & 1);
        tm >>= 1;
    }
 
    cout << dfs(40, len, n >> 40) << endl;
 
}