权值线段树（动态开点）

介绍

权值线段树

权值线段树用于维护一定值域内，各个元素出现的次数，结合动态开点可以 避免离散化的处理。

举个例子，我们现在有一个长度为 $10$ 的数组 $[1,5,2,3,4,1,3,4,4,4]$

$1$ 出现了 $2$ 次，$2$ 出现了 $1$ 次，$3$ 出现了 $2$ 次，$4$ 出现了 $4$ 次，$5$ 出现了 $1$ 次。

则这个线段树长这样：

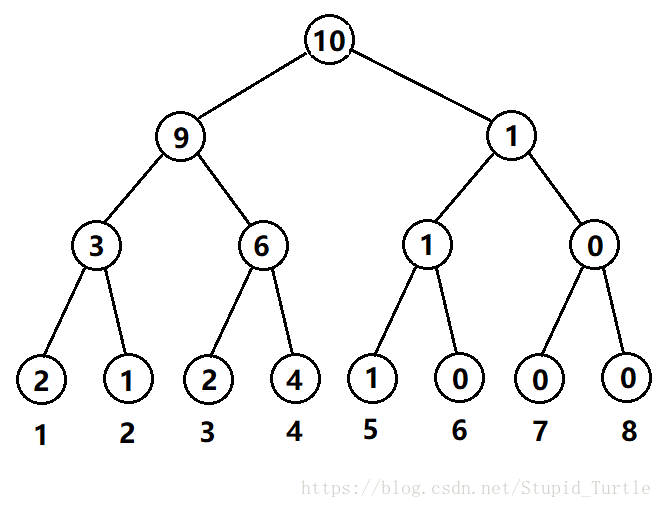
images

每个叶子节点的值：代表 这个值的出现次数。

非叶子节点的值：代表了某一个值域内，所有值出现次数的和。

动态开点

我们会发现，在上面的线段树中，$6,7,8$ 都没有出现过，所以值为 $0$。

$7,8$ 对应节点的 parent 的值也为 $0$，这样很浪费空间。而且在值域较大的时候（如维护 $[1,10^{18}]$ 的权值线段树）时，这样开点是不可行的。

所以我们可以用 动态开点 来解决空间问题。

动态开点与普通线段树的区别，主要在于以下几个方面：

一个节点的左右 child 不一定为 cur<<1, cur<<1|1，而是以 lc, rc 的形式储存在 struct 中。
更改某一个节点的值，或者 push_down() 时，如果节点不存在，则创建一个。
询问某一个节点的值时，如果节点不存在，直接返回 $0$。
不需要 build() 线段树，因为在一开始，整个线段树没有任何节点。

这样做有什么好处呢？

大幅度节省空间，尤其对于值域较大的权值线段树。
如果一个数组初始状态均为 $0$，就避免了普通线段树需要 build() 的过程。如果需要初始化，则一个个 insert() 进去也可以。
在需要维护多棵线段树时（比如 $HDU ~6183$ 需要开 $51$ 棵动态开点线段树），可以将它们维护在同一个数组上，大幅度节省空间。

例题

例1 洛谷P1908 逆序对

题解

求逆序对，我们可以从左往右遍历数组，遍历到 $i$ 时，检查一下已经遍历的值中，有多少比它大的即可。

这可以用权值线段树来实现。

因为每个数字的范围是 $[1,10^9]$，所以需要动态开点。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e7+5;

struct node {
    int lc, rc, cnt;  // 记录左右child的编号，如果不存在，则为 0
} tr[maxn];
int id = 0;   // 动态开点用的pointer
int root = 0;  // 根节点编号

void push_up(int cur) {
    int lc = tr[cur].lc, rc = tr[cur].rc;
    tr[cur].cnt = tr[lc].cnt + tr[rc].cnt;
}

// 插入一个值为 p 的元素
void insert(int& cur, int l, int r, int p) {
    if (!cur) cur = ++id;  // 动态开点
    if (l == r) {
        tr[cur].cnt++;
        return;
    }
    int mid = (l+r) >> 1;
    if (p <= mid) insert(tr[cur].lc, l, mid, p);
    if (p > mid) insert(tr[cur].rc, mid+1, r, p);
    push_up(cur);
}

// 询问 值在 [L,R] 之间的元素有多少个
ll query(int cur, int l, int r, int L, int R) {
    if (!cur) return 0;
    if (l >= L && r <= R) {
        return (ll)tr[cur].cnt;
    }
    int mid = (l+r) >> 1;
    ll res = 0;
    if (L <= mid) res += query(tr[cur].lc, l, mid, L, R);
    if (R > mid) res += query(tr[cur].rc, mid+1, r, L, R);
    return res;
}

int main() {
    int n; cin >> n;
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        insert(root, 1, 1e9+1, x);
        ans += query(1, 1, 1e9+1, x+1, 1e9+1);
    }
    cout << ans << endl;
}

例2 CF69E Subsegments

题意

给定正整数 $n,k$，给定一个长度为 $n$ 的数组 $a_1,a_2,…,a_n$。

输出 $n-k+1$ 个数，每个数字代表 $[a_{i},…, a_{i+k-1}]$ 中，仅出现一次的元素的最大值。

如果不存在仅出现一次的元素，输出 $-1$。

其中，$n \leq 10^5, 1 \leq k \leq n, |a_i| \leq 10^9$

题解

在线段树节点里面额外维护一个信息 bool one，代表这个值域内，是否存在仅出现一次的元素。然后询问时，优先询问右边（值域较大的部分）。

还有一个问题，$a_i$ 的值可以为负数，怎么维护？

我们可以将 $a_i$ 都加上一个 delta = 1e9，这样让每一个 $a_i \geq 0$，然后就可以用权值线段树来维护了。记得在 insert(), query() 时，也要加上这个 delta = 1e9。

注：我们用 int mid = (r-l) / 2 + l 来代替 int mid = (l+r) >> 1，防止 overflow。

证明它们两个的等效性：因为 (r-l) 和 (l+r) 的奇偶性一样，且均为非负数，所以它们等效。

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e7+5;
const int maxm = 1e5+10;

int n,k,id = 0, root = 0;
struct node {
    int lc,rc,cnt;
    bool one;  // 这个值域内，是否存在unique的元素
} tr[maxn];
int arr[maxm];

void push_up(int cur) {
    int lc = tr[cur].lc, rc = tr[cur].rc;
    tr[cur].one = tr[lc].one | tr[rc].one;
    tr[cur].cnt = tr[lc].cnt + tr[rc].cnt;
}

void insert(int& cur, int l, int r, int p, int f) {
    if (!cur) cur = ++id;
    if (l == r) {
        tr[cur].cnt += f;
        if (tr[cur].cnt == 1) tr[cur].one = 1;
        else tr[cur].one = 0;
        return;
    }
    int mid = (r - l) / 2 + l;
    if (p <= mid) insert(tr[cur].lc, l, mid, p, f);
    if (p > mid) insert(tr[cur].rc, mid+1, r, p, f);
    push_up(cur);
}

int query(int cur, int l, int r) {
    if (!tr[cur].one) return -1;
    if (l == r) return l;
    int lc = tr[cur].lc, rc = tr[cur].rc;
    int mid = (r - l) / 2 + l;
    if (tr[rc].one) return query(rc, mid+1, r);
    else return query(lc, l, mid);
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> arr[i];
    for (int i = 1; i <= k-1; i++) {
        insert(root, 0, 2e9, arr[i]+1e9, 1);
    }
    for (int i = k; i <= n; i++) {
        insert(root, 0, 2e9, arr[i]+1e9, 1);
        int a = query(root, 0, 2e9);
        if (a == -1) {
            cout << "Nothing" << "\n";
        } else {
            cout << (a - (int)1e9) << "\n";
        }
        insert(root, 0, 2e9, arr[i-k+1]+1e9, -1);
    }
}

例3 CF474E Pillars

题意

给定正整数 $n,d$，还有长度为 $n$ 的数组 $h_1,h_2,…,h_n$。

求数组中 最长的 subsequence $b$（不一定连续），使得 $\forall i, |b_{i+1} - b_i| \geq d$。

其中，$n \leq 10^5, 0 \leq d \leq 10^9, 1 \leq h_i \leq 10^{15}$

题解

一个很明显的 dp 思路：

当我们遍历到 $i$ 时，令 $dp[j]$ 为：目前为止，结尾的值为 $j$ 的 subsequence 的最大长度。

那么 $dp[h_i] = \max\limits_j \{ dp[j]+1 \}$，其中 $|h_i - j| \geq d$

那么，这个 dp 数组就可以用权值线段树来维护。

查询的时候，分别查询 $j \geq h_i + d$ 和 $j \leq h_i - d$ 的部分即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 8e6;
const int maxm = 1e5+10;

int n, pre[maxm], dp[maxm];
ll arr[maxm], d;
int root,id;
struct node {
    int lc,rc,m,idx;  // m: dp数组的值，idx: 该值域内，具有最大的 m 对应的原来array中的index
} tr[maxn];

void push_up(int cur) {
    int lc = tr[cur].lc, rc = tr[cur].rc;
    if (tr[lc].m > tr[rc].m) tr[cur].m = tr[lc].m, tr[cur].idx = tr[lc].idx;
    else tr[cur].m = tr[rc].m, tr[cur].idx = tr[rc].idx;
}

void insert(int& cur, ll l, ll r, ll h, ll m, int idx) {
    if (!cur) cur = ++id;
    if (l == r) {
        if (m > tr[cur].m) {
            tr[cur].m = m;
            tr[cur].idx = idx;
        }
        return;
    }
    ll mid = (l+r) >> 1;
    if (h <= mid) insert(tr[cur].lc, l, mid, h, m, idx);
    if (h > mid) insert(tr[cur].rc, mid+1, r, h, m, idx);
    push_up(cur);
}

// return the index with maximum m value
pll query(int cur, ll l, ll r, ll L, ll R) {
    if (!cur) return {0,0};
    if (l >= L && r <= R) {
        return {tr[cur].m, tr[cur].idx};
    }
    ll mid = (l+r) >> 1;
    pll r1, r2;
    if (L <= mid) r1 = query(tr[cur].lc, l, mid, L, R);
    if (R > mid) r2 = query(tr[cur].rc, mid+1, r, L, R);
    if (r1.first > r2.first) return r1;
    return r2;
}

const ll up = 1e15 + 2e9 - 1LL;
const ll delta = 1e9-1;
int ans = 0, maxi = 0;
int main() {
    cin >> n >> d;
    for (int i = 1; i <= n; i++) cin >> arr[i];
    for (int i = 1; i <= n; i++) {
        ll h = arr[i];
        pll r1 = query(root, 0, up, 0, h-d+delta);
        pll r2 = query(root, 0, up, h+d+delta, up);
        pll r;
        if (r1.first > r2.first) r = r1;
        else r = r2;
        dp[i] = dp[r.second] + 1;
        pre[i] = r.second;
        insert(root, 0, up, h+delta, dp[i], i);
        if (ans < dp[i]) ans = dp[i], maxi = i;
    }
    vector<int> vec;
    while (maxi) {
        vec.push_back(maxi);
        maxi = pre[maxi];
    }
    cout << vec.size() << endl;
    for (int i = vec.size()-1; i >= 0; i--) {
        cout << vec[i] << " ";
    }
    cout << endl;
}

例4 HDU6183 Color it

题意

给定一个二维平面，初始状态下，整个平面为空，现在有以下 3 种操作：

$0$：清空平面

$1 ~ x ~ y ~ c$：在 $(x,y)$ 添加一种颜色 $c$

$2 ~x~ y_1~ y_2$：查询所有 $(a,b)$ 的不同颜色数量，其中 $1 \leq a \leq x, y_1 \leq b \leq y_2$

其中，$1\leq x,y \leq 10^6, 0 \leq c \leq 50$

数据保证，最多有 $150000$ 个连续的询问 $1$，最多有 $10$ 个询问 $0$。

题解

首先，发现颜色 $c$ 只有 $51$ 种，所以我们可以分开维护每一种颜色，统计的时候加起来就可以了。

其次，发现本题询问 $2 ~x~ y_1~ y_2$ 时，我们只关心 $1 \leq a \leq x$ 的部分，也就是说，对于同一种颜色和同一个 $y$ 坐标而言，我们只关心 最小的那个 $x$ 坐标。

所以，我们可以根据 $y$ 轴开一棵线段树，维护 $y$ 坐标对应的最小 $x$ 值。

有 $51$ 种颜色，所以我们开 $51$ 棵线段树即可。

注：如果开51棵普通的线段树会 $MLE$，所以用动态开点，把它们开在同一个数组上，使用 int root[51] 来维护 $51$ 棵线段树的 root 即可。

注：如果询问是 $1 ~ x_1 ~ x_2 ~ y_1 ~ y_2$ 的这种形式，似乎要用 线段树套线段树 （还没学）。

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn = 8e6;

int id = 0;
int root[51];
struct node {
    int lc,rc,x = 1e9;
} tr[maxn];

void push_up(int cur) {
    int lc = tr[cur].lc, rc = tr[cur].rc;
    tr[cur].x = min(tr[lc].x, tr[rc].x);
}

void insert(int& cur, int l, int r, int c, int x, int y) {
    if (!cur) cur = ++id;
    if (l == r) {
        tr[cur].x = min(tr[cur].x, x);
        return;
    }
    int mid = (l+r) >> 1;
    if (y <= mid) insert(tr[cur].lc, l, mid, c, x, y);
    else insert(tr[cur].rc, mid+1, r, c, x, y);
    push_up(cur);
}

bool query(int cur, int l, int r, int c, int x, int L, int R) {
    if (!cur) return 0;
    if (l >= L && r <= R) {
        return tr[cur].x <= x;
    }
    int mid = (l+r) >> 1;
    bool res = 0;
    if (L <= mid) res |= query(tr[cur].lc, l, mid, c, x, L, R);
    if (res) return 1;
    if (R > mid) res |= query(tr[cur].rc, mid+1, r, c, x, L, R);
    return res;
}

void init(int i) {
    tr[i].lc = tr[i].rc = 0;
    tr[i].x = (int)1e9;
}

void clearall() {
    for (int i = 0; i <= 50; i++) {
        root[i] = 0;
    }
    for (int i = 1; i <= id; i++) init(i);
    id = 0;
}

int main() {
    int op;
    while (1) {
        cin >> op;
        if (op == 0) clearall();
        if (op == 1) {
            int x,y,c;
            cin >> x >> y >> c;
            insert(root[c], 1, 1e6, c, x, y);
        }
        if (op == 2) {
            int ans = 0;
            int x,y1,y2; cin >> x >> y1 >> y2;
            if (y1 > y2) swap(y1,y2);
            for (int c = 0; c <= 50; c++) {
                ans += query(root[c], 1, 1e6, c, x, y1, y2);
            }
            cout << ans << "\n";
        }
        if (op == 3) {
            return 0;
        }
    }
}

Contents

介绍