树上差分
Contents
介绍
树上差分就是将数组上的差分思想,转化到树上。
树上差分是一种思想,很多时候树链剖分可以代替树上差分,如果询问不复杂的时候,就可以用树上差分来减少代码难度。
经典模型
模型1 边权求和
题意
给定一个 $N$ 个节点的树,每个边 edge上都有权值(初始为0)。
给定 $M$ 次操作,每次将 $u,v$ 之间的路径的 edge权值 加上 $d$。
所有操作结束后,求所有边上的权值?
首先将树变成有根树(设 $root = 1$),我们令 dp[u] 为:从 $root$ 开始,一直到 $u$ 的路径上的所有边权,都被加上了 dp[u]。
那么每次修改操作 $u,v,d$,令 $x = LCA(u,v)$,则修改操作是:
dp[u] += d, dp[v] += d, dp[x] -= 2 * d
所有修改操作结束后,我们将 dp[] 的值 从下往上 进行传递(用 dfs() 实现即可)。就可以得到所有的边权了。
• 在 dfs(u, p) 的过程中,$(u, to)$ 这个edge的权值就是 dp[to]。
int dp[maxn];
void dfs(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u); // 注意是先 dfs, 再 dp[u] += dp[to](从下到上)
dp[u] += dp[to];
// dp[to] 就是 (u,to) 这个边的权值
}
}
模型2 点权求和
题意
给定一个 $N$ 个节点的树,每个点 vertex上都有权值(初始为0)。
给定 $M$ 次操作,每次将 $u,v$ 之间的路径的 vertex权值 加上 $d$。
所有操作结束后,求所有点上的权值?
同理,令 dp[u] 为:从 $root$ 开始,一直到 $u$ 的路径上的所有点权(inclusive),都被加上了 dp[u]。
那么每次修改操作 $u,v,d$,令 $x = LCA(u,v)$,则修改操作是:
dp[u] += d, dp[v] += d, dp[x] -= d, dp[par[x]] -= d
所有修改操作结束后,我们将 dp[] 的值 从下往上 进行传递。
• 代码同上。
模型3 子树求和
题意
给定一个 $N$ 个节点的树,每个点 vertex上都有权值(初始为0)。
给定 $M$ 次操作,每次将 $u$ 的子树的 vertex权值 加上 $d$。
所有操作结束后,求所有点上的权值?
令 dp[u] 为:$u$ 的子树中的 vertex 权值都被加上了 dp[u]。
那么每次修改操作 $u, d$,有:
dp[u] += d
所有修改操作结束后,我们将 dp[] 的值 从上往下 进行传递。(注意这里的顺序是从上往下)
int dp[maxn];
void dfs(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dp[to] += dp[u]; // 注意是先 dp[to] += dp[u] (从上到下),再 dfs
dfs(to, u);
}
}
例题
例1 AcWing 352 暗之连锁
题意
给定一棵包含 $N$ 个节点的树,树中原先存在的边叫做主要边。
现在给定 $M$ 个附加边。
我们需要采取以下操作(仅能进行一次,并且步骤1,2都必须进行):
- 选定一个主要边,删掉它。
- 然后选定一个附加边,删掉它。
求有多少种这样的操作,使得树断开?
其中,$N \leq 10^5, M \leq 2 \times 10^5$
题解
因为我们是先删除主要边,再删除附加边。在删除一个主要边 $(u,v)$ 的时候,我们只要关心删除附加边后,能否让 $(u,v)$ 断开。
我们可以只考虑 主要边,对于附加边,我们把它们转化为 主要边。
也就是说,对于每个附加边 $(u,v)$,我们都把 $(u,v)$ 在原来树中的路径上,所有 edge(主要边)的权值都加 $1$。
所以,在进行删除操作的第一步(删除主要边)时,我们可以看一下这个边 $(u,v)$ 的权值。有以下三种情况:
- 权值等于 $0$:树已经断开了,附加边随便删一条即可,所以
ans += M。 - 权值等于 $1$:存在,且仅存在一个附加边,使得 $u,v$ 仍然连通,所以
ans++。 - 权值大于等于 $2$:存在多个附加边使得 $u,v$ 仍然连通,所以不可能使得树断开。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int par[maxn][19], head[maxn], ecnt = 1, n, m, dep[maxn], dp[maxn];
ll ans = 0;
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void dfs(int u, int p) {
par[u][0] = p;
dep[u] = dep[p] + 1;
for (int j = 1; j <= 18; j++) par[u][j] = par[par[u][j-1]][j-1];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
}
}
int jump(int u, int d) {
for (int j = 0; j <= 18; j++)
if (d & (1<<j)) u = par[u][j];
return u;
}
int LCA(int u, int v) {
if (dep[u] < dep[v]) swap(u,v);
int diff = dep[u] - dep[v];
u = jump(u, diff);
if (u == v) return u;
for (int j = 18; j >= 0; j--) {
if (par[u][j] != par[v][j]) u = par[u][j], v = par[v][j];
}
return par[u][0];
}
void dfs2(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs2(to, u);
dp[u] += dp[to];
if (dp[to] == 0) ans += (ll)(m);
if (dp[to] == 1) ans++;
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u, v); addEdge(v, u);
}
dfs(1, 0);
for (int i = 1; i <= m; i++) {
int u, v; cin >> u >> v;
int p = LCA(u,v);
dp[u]++, dp[v]++, dp[p] -= 2;
}
dfs2(1, 0);
cout << ans << endl;
}
例2 CF1076E Vasya and a Tree
题意
给定 $n$ 个节点的有根树($1$ 为根)。每个vertex上都有一个权值,初始为 $0$。
有 $m$ 个询问,每次询问:
$u ~ d ~ x$:将 $u$ 的子树中,离 $u$ 的距离 $\leq d$ 的所有 vertex,权值都加上 $x$。
求所有询问结束后,每个节点上的权值?
法一(树上差分)
首先看一下我们怎么进行差分:
将 $u$ 的子树中,离 $u$ 的距离 $\leq d$ 的所有 vertex,权值都加上 $x$。
我们可以将上面转化为:
- 将 $u$ 的子树权值都加上 $x$
- 然后将 $u$ 距离 $= (d+1)$ 的所有 $v$ 的子树,权值都减去 $x$。
注意到,每次询问,加的都是 子树。
那么我们可以利用 dfs() 的特点,不需要考虑每次询问加的是哪个节点,而是将询问根据 每个节点的 dep[] 来进行修改,在递归的时候自然就完成了差分,在 dfs() 回溯的时候,再把修改 revert 掉。
具体操作如下:
- 离线处理所有的询问,记录每一个节点上,都有哪些询问。
dfs(u)的时候,将sum[dep[u]] += x,然后sum[dep[u]+d+1] -= x- 回溯的时候,将修改 revert,即:
sum[dep[u]] -= x,然后sum[dep[u]+d+1] += x
记得下传 dp[] 数组的值。
法一 代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5;
int n, m, head[maxn], ecnt = 1, dep[maxn];
ll sum[maxn], ans[maxn], dp[maxn]; // dp[u] 代表u的subtree加上了多少
vector<pii> q[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void dfs(int u, int p) {
dep[u] = dep[p] + 1;
for (auto pa : q[u]) {
int d = pa.first;
ll x = pa.second;
sum[dep[u]] += x;
d = min(3e5, d + dep[u] + 1);
sum[d] -= x;
}
dp[u] += sum[dep[u]];
ans[u] = dp[u];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dp[to] += dp[u];
dfs(to, u);
}
for (auto pa : q[u]) {
int d = pa.first;
ll x = pa.second;
sum[dep[u]] -= x;
d = min(3e5, d + dep[u] + 1);
sum[d] += x;
}
}
int main() {
fastio;
cin >> n;
for (int i = 1; i < n; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
cin >> m;
while (m--) {
int u,d,x; cin >> u >> d >> x;
q[u].push_back({d, x});
}
dfs(1,0);
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << endl;
}
法二(BFS序 + 二分 + 差分数组)
BFS序就是从上到下,从左到右,一层层的进行编号。
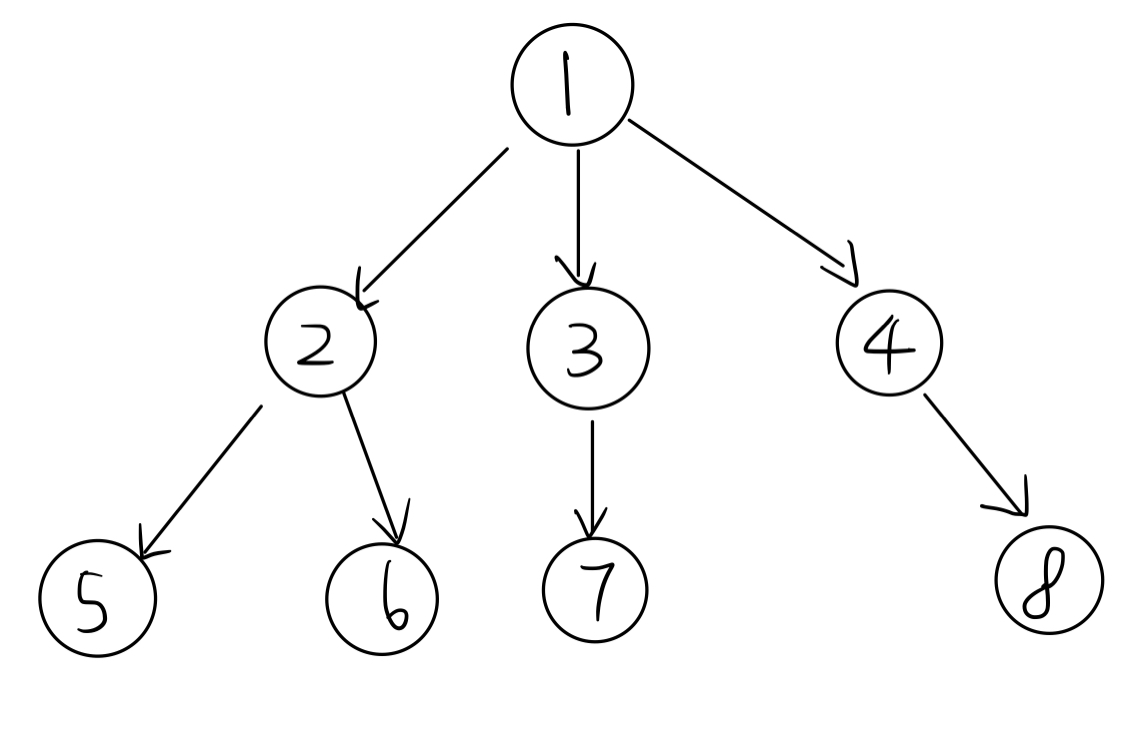
求 BFS 序用一个普通的 BFS 就可以解决:
int q[maxn], hd = -1, tail = 0, idcnt = 0, id[maxn];
void bfs() {
q[++tail] = 1;
while (hd <= tail) {
int cur = q[hd++];
id[cur] = ++idcnt;
mp[idcnt] = cur;
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[cur][0]) continue;
q[++tail] = to;
}
}
}
有了 BFS 序以后,我们可以发现:
$u$ 的子树中,离 $u$ 的距离 $= d+1$ 的所有 vertex 实际上就是 BFS 序上,一段连续的编号。
所以,我们只要找到这一段编号即可。
我们可以利用 二分搜索 来查找这一段编号的 左端点和右端点。
查找端点的时候,我们看一下当前端点编号为 $mid$,往上跳 $d+1$ 格的端点编号即可。
令 $mid$ 往上跳 $d+1$ 格的端点为 $p$:
- $id[p] < id[u]$:说明端点在 $x$ 的右侧,
l = mid+1 - $id[p] > id[u]$:说明端点在 $x$ 的左侧,
r = mid-1 - $id[p] = id[u]$:如果是在查找左端点,那么左端点在左侧,则
r = mid-1;否则右端点在右侧,则l = mid+1。
由此可以找到左右端点,然后维护一个差分数组,进行一下区间修改即可。
法二 代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5;
const int maxm = 2e5+2;
int n, m, q[maxn], head[maxn], hd = 0, tail = -1, ecnt = 1, id[maxn], mp[maxn], idcnt = 0; // id[u]: vertex u的id, mp[id]: id对应的vertex u
int par[maxn][20], dep[maxn];
ll sum[maxn], dp[maxn]; // sum 为差分数组, dp[u] 代表u的subtree加上了多少
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
int jump(int u, int d) {
for (int j = 0; j <= 19; j++) {
if (d & (1<<j)) u = par[u][j];
}
return u;
}
void dfs(int u, int p) {
dep[u] = dep[p] + 1;
par[u][0] = p;
for (int j = 1; j <= 19; j++) par[u][j] = par[par[u][j-1]][j-1];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
}
}
void bfs() {
q[++tail] = 1;
while (hd <= tail) {
int cur = q[hd++];
id[cur] = ++idcnt;
mp[idcnt] = cur;
for (int e = head[cur]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[cur][0]) continue;
q[++tail] = to;
}
}
}
inline void add(int l, int r, ll val) {
if (l == -1) return; // 不存在这样的点
sum[l] += val, sum[r+1] -= val;
}
void update(int u, int d, ll x) {
int L = -1, R = -1;
int l = id[u], r = n;
while (l <= r) {
int mid = (l+r) >> 1;
int p = jump(mp[mid], d+1);
if (id[p] < id[u]) l = mid+1;
if (id[p] > id[u]) r = mid-1;
if (id[p] == id[u]) {
L = mid;
r = mid-1;
}
}
l = id[u], r = n;
while (l <= r) {
int mid = (l+r) >> 1;
int p = jump(mp[mid], d+1);
if (id[p] < id[u]) l = mid+1;
if (id[p] > id[u]) r = mid-1;
if (id[p] == id[u]) {
R = mid;
l = mid+1;
}
}
add(L, R, -x);
add(id[u], id[u], x);
}
void dfs2(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dp[to] += dp[u];
dfs2(to, u);
}
}
int main() {
fastio;
cin >> n;
for (int i = 1; i < n; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
dfs(1,0);
bfs();
cin >> m;
while (m--) {
int u,d,x; cin >> u >> d >> x;
update(u, d, x);
}
for (int i = 1; i <= n; i++) sum[i] += sum[i-1], dp[mp[i]] = sum[i];
dfs2(1, 0);
for (int i = 1; i <= n; i++) cout << dp[i] << " ";
cout << endl;
}
例3 CF1467E Distinctive Roots in a Tree
题意
给定 $n$ 个节点的树,每个节点 $i$ 上有一个值 $a_i$。
定义一个节点 $u$ 为 distinctive root,如果:
从 $u$ 出发,连向任意一个节点 $v$ 的路径上,不存在相同的值。
输出整个树内,distinctive root 的数量。
其中,$1 \leq n \leq 2 \times 10^5, 1 \leq a_i \leq 10^9$
题解
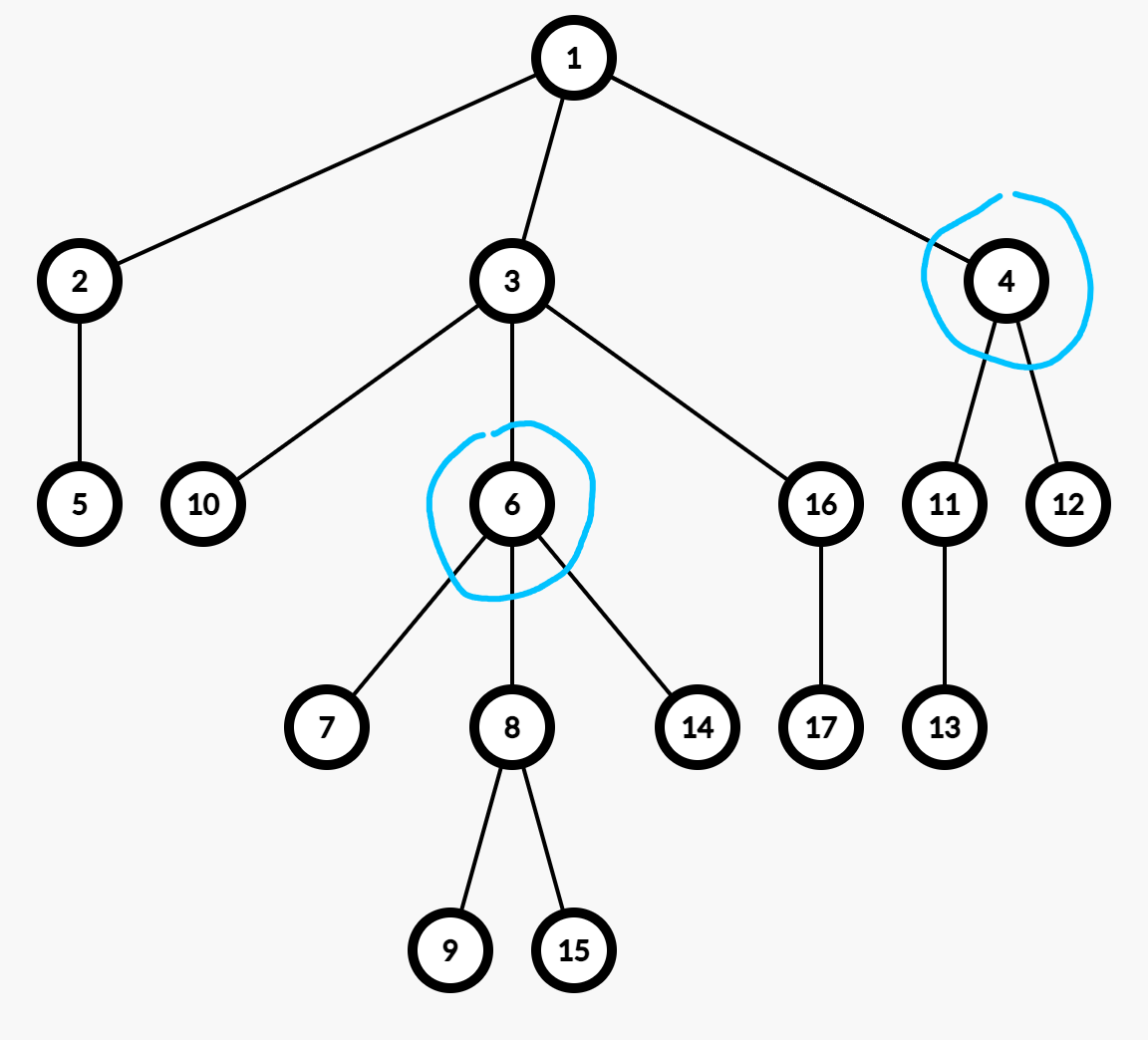
首先转化成有根树(以 $1$ 为根)。然后我们看,对于任意的两个具有相同权值的节点 $u,v$($a_u = a_v$),可以分为两种情况:
令 $x = LCA(u,v)$
- $x \neq u, x \neq v$
- $x = u$ 或者 $x = v$
以下,用蓝色圈起来的节点,代表权值相同
Case 1: $x \neq u, x \neq v$
可以发现,在本图中,所有 不可能为 distinctive root 的节点,为 $4$ 的子树 和 $6$ 的子树。
Case 2: $x = u$ 或者 $x = v$
在本图中,除了 节点 $6,7,14$ 以外,全都 不可能为 distinctive root。
由上,我们可以总结出以下结论:
**情况1:**$x \neq u, x \neq v$,那么
- $u$ 的子树 $R_u$
- $v$ 的子树 $R_v$
均不可能为 distinctive root。
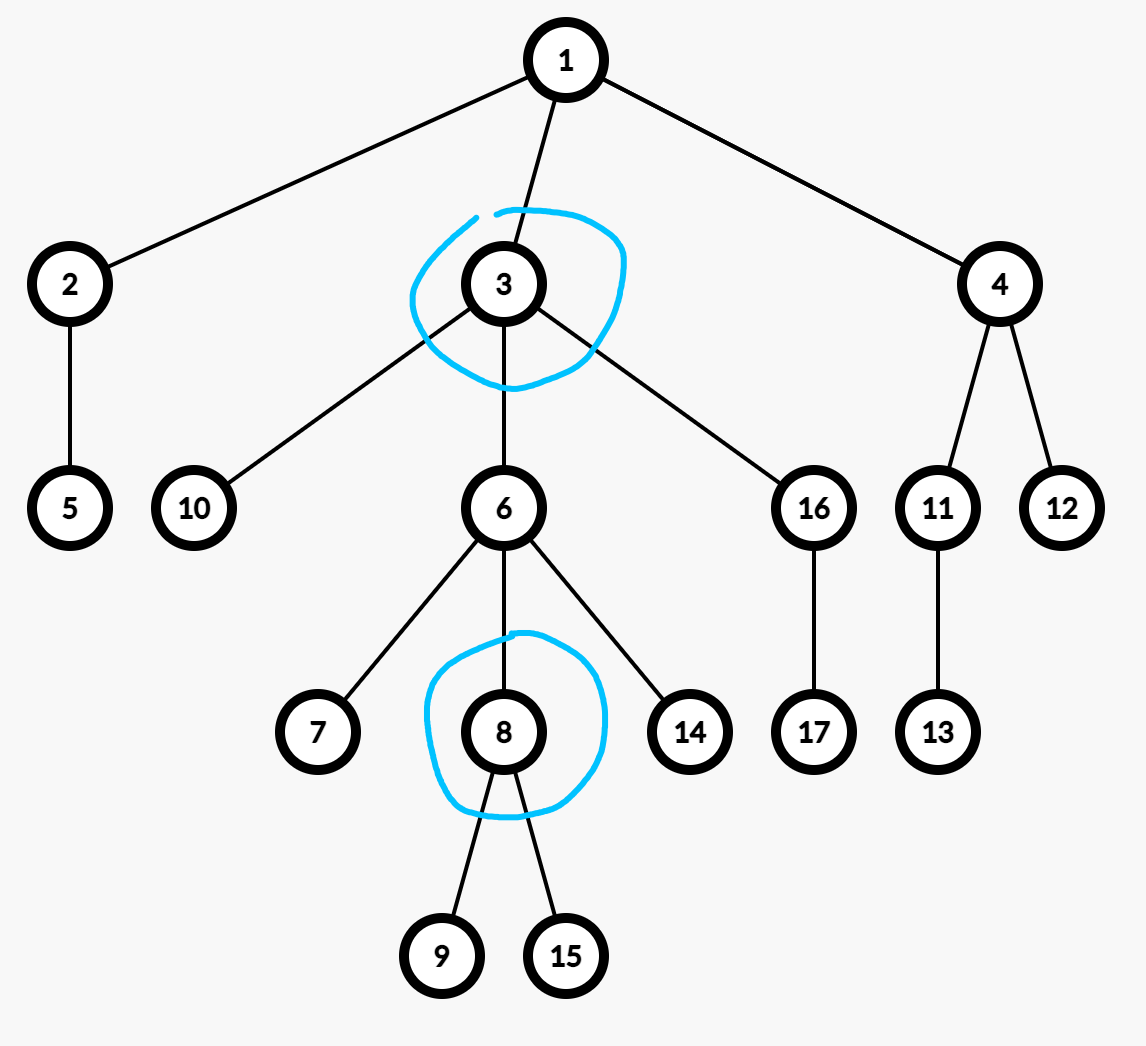
**情况2:**$x = u$ 或者 $x = v$,我们假设 $v$ 包含在 $u$ 的子树内。则
- $v$ 的子树 $R_v$
- $u$ 外面的所有节点
- $u$ 的所有child的子树(除了 $v$ 所在的那个子树以外)
均不可能为 distinctive root。
例子:如上图中,$u = 3, v = 8$,那么 $u=3$ 有三个子树 $R_{10}, R_6, R_{16}$,因为 $v=8 \in R_6$,所以 $R_6$ 不受影响。
有了上述结论,我们需要思考如何高效的处理。首先我们不可能直接枚举所有权值相同的点对 $(u,v)$。
对于这一类问题,一个比较常见的套路是:
维护一个 cnt[] 的桶,在 dfs() 过程中,对当前节点进行统计。
将上述情况做一个转化:
对于情况 $1$,我们可以转化为:当我们 dfs(u) 时,看一下 $u$ 的外面是否存在 $v$ 使得 $a_u = a_v$。如果存在,将 $u$ 的所有子树进行标记。
对于情况 $2$,我们可以转化为:当我们 dfs(u) 时,看一下 $u$ 的某一个子树 $R_j$ 内,是否存在 $v$ 使得 $a_u = a_v$。如果存在,将 除了该子树 $R_j$ 以外 的所有子树都进行标记,然后将 $v$ 的子树 $R_v$ 也进行标记。
现在问题转化为:
对于每个节点 $u$,如何知道:
- $u$ 的外面是否存在 $v$ 使得 $a_u = a_v$ ?
- $u$ 的所有child $j$ 的子树 $R_j$ 内,是否存在 $v$ 使得 $a_u = a_v$ ?
这里,就要用到 桶思想。
先预处理出整棵树的信息 all[],其中 all[v] 代表 整棵树内 权值为 $v$ 的节点数量。
维护一个 cnt[],其中 cnt[v] 代表 当前遇到的 权值为 $v$ 的节点数量。
在我们 dfs(u) 前,我们看一下 cnt[a[u]] 的值。
在我们 dfs(u) 结束后,再看一下 cnt[a[u]] 的值。
-
如果在
dfs(u)之前,cnt[a[u]] = 0。在dfs(u)结束后,cnt[a[u]] = all[a[u]],说明 $u$ 外面不存在 $v$ 使得 $a_u = a_v$。否则,存在。 -
如果在
dfs(to)之前($to$ 为 $u$ 的child)和之后,cnt[a[u]]增加了,说明 $to$ 这个child的子树内,存存在 $v$ 使得 $a_u = a_v$。
标记子树就是套路的树上差分了。不再赘述。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
int n;
struct Edge {
int to, nxt;
} edges[maxn<<1];
map<int,int> all, cnt;
int dp[maxn], f[maxn]; // dp代表标记,f代表处理完以后的值,大于0就说明不行
int val[maxn], head[maxn], ecnt = 1;
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
void dfs1(int u, int p) {
all[val[u]]++;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, u);
}
}
void dfs2(int u, int p) {
int v = val[u];
int pcnt = cnt[v];
cnt[v]++;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
int pre = cnt[v];
dfs2(to, u);
if (cnt[v] - pre > 0) { // 里面存在 cur
dp[to]--;
dp[1]++;
}
}
if (cnt[v] - pcnt < all[v]) { // 外面存在 cur
dp[u]++;
}
}
int ans = 0;
void dfs3(int u, int p) {
f[u] += dp[u];
if (f[u] == 0) ans++;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dp[to] += dp[u]; // 标记下传
dfs3(to, u);
}
}
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) cin >> val[i];
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v), addEdge(v,u);
}
dfs1(1, 0);
dfs2(1, 0);
dfs3(1, 0);
cout << ans << endl;
}
例4 洛谷P1600 [NOIP2016 提高组] 天天爱跑步
题意
给定一棵 $n$ 个节点的树。有 $m$ 个玩家,第 $i$ 个玩家的起点为 $s_i$,终点为 $t_i$。所有玩家从第 $0$ 秒开始,以每秒跑 $1$ 条边的速度,沿着最短路径从 $s_i$ 跑到 $t_i$。
现在给出 $n$ 个数字 $w_i$,对于每个数字 $i$,我们需要回答在 第 $w_i$ 秒时,有多少个玩家恰好站在节点 $i$ 上。
• 当玩家 $i$ 跑到终点 $t_i$ 后,他会退出游戏。如果他刚好在第 $w_{t_i}$ 秒跑到了节点 $t_i$,那么他会被算入答案中。否则不会被算入。
其中,$n,m \leq 3 \times 10^5, 1 \leq s_i,t_i \leq n, 0 \leq w_i \leq n$
题解
先考虑一下,我们能否对于每一个玩家,考虑他的贡献?
似乎不行。因为每个节点的 $w_i$ 各不相同,我们没法将一条路径 $(s_i,t_i)$ 上的贡献直接算出来。
既然每个节点的 $w_i$ 不同,不妨考虑对于每个节点 $i$,我们看有多少个玩家满足条件。
同上题一样,一个常规的套路是
维护一个 cnt[] 的桶,在 dfs() 过程中,对当前节点进行统计。
那么,这个桶里面需要维护什么信息?
首先将树变成有根树(根节点为 $1$),这样每个节点最多只有一个 parent(如果一个节点 $u$ 具有两个 parent $p_1,p_2$,则 $1,p_1,p_2,u$ 成环)。
所以我们会发现,如果一个玩家 $(s_i,t_i)$ 可能对 $u$ 产生贡献的话,$s_i, t_i$ 的其中至少有一个在 $u$ 的子树内!
但是,如果只是用一个 cnt[] 来记录,我们无法区分哪个是 $s_i$,哪个是 $t_i$,我们不如分开讨论。
令 $x_i = LCA(s_i, t_i)$,则路径可以分成两段:$s_i \rightarrow x_i$(路径上行) 和 $x_i \rightarrow t_i$ (路径下行)。由于区分了上下行路线,也可以很方便的用 cnt[] 记录深度信息。
对于上行路线,只考虑 $s_i$ 的影响。如果 $u$ 在 $s_i \rightarrow x_i$ 的上行路径上,就可以考虑 $s_i$ 带给 $u$ 的贡献。
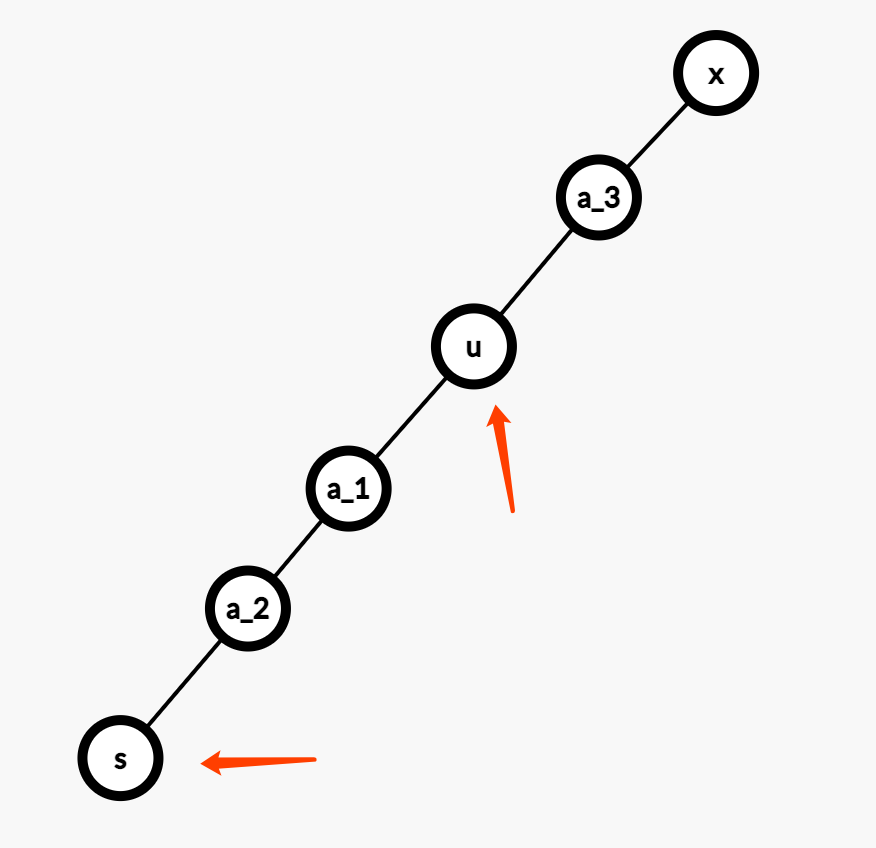
对于这个 $s$,只要满足 $dep[s] - dep[u] = w_u$,即:
$$dep[u] + w_u = dep[s]$$
所以在 dfs(u) 的过程中,第 $1$ 个需要维护的桶 ds[],可以用来维护 dep[s] 的数量,即:
ds[d] 的值为:在 $u$ 的子树内,有多少个节点的 dep = d。
对于下行路线,只考虑 $t_i$ 的影响。如果 $u$ 在 $x_i \rightarrow t_i$ 的下行路径上,就可以考虑 $t_i$ 带给 $u$ 的贡献。
但是,我们不能单独考虑 $t_i$,因为是否产生贡献,主要是根据 $s_i$ 决定的。我们在考虑 $t_i$ 的时候无法忽略 $s_i$ 的影响。这时候我们要将 $s_i$ 和 $t_i$ 结合起来,变成一个信息,使得我们可以直接用桶来维护。
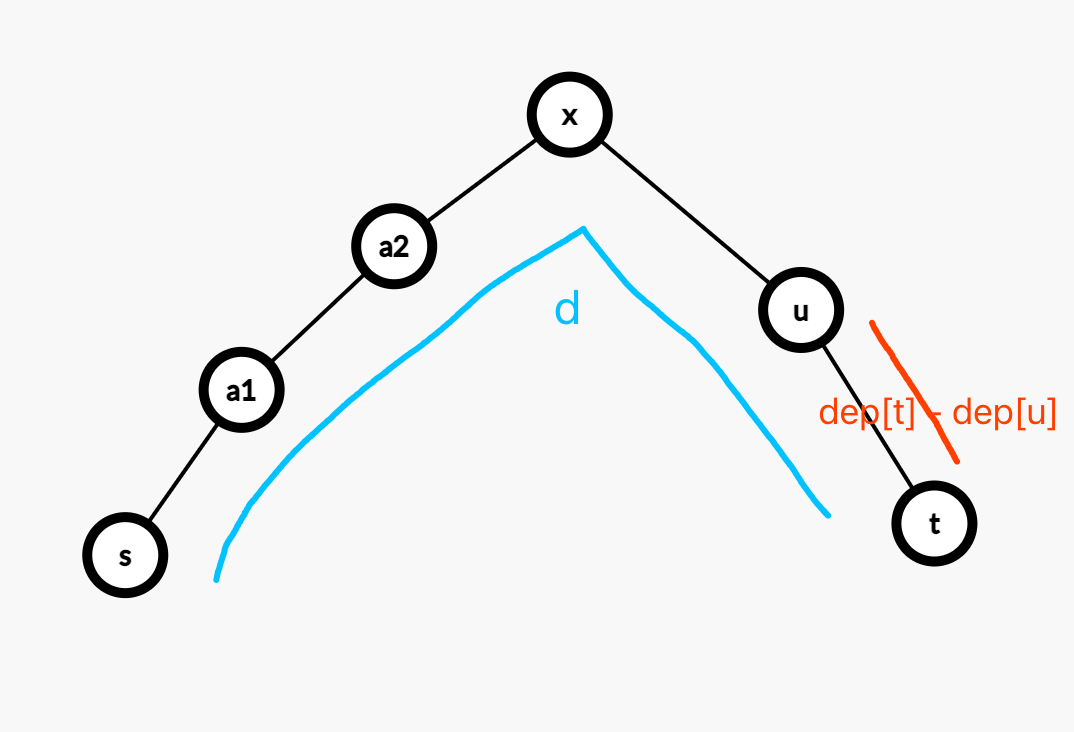
带 $s_i$ 的信息不好维护,我们可以预先处理出 $d$,代表 $s_i,t_i$ 这两个节点之间的距离。然后从 $u \rightarrow t$ 的距离是 $dep[t] - dep[u]$。所以只要满足 $d - (dep[t] - dep[u]) = w_u$,也就是:
$$w_u - dep[u] = d - dep[t]$$
所以在 dfs(u) 的过程中,第 $2$ 个需要维护的桶 dt[],可以用来维护 d - dep[t] 的数量,即:
dt[a] 的值为:在 $u$ 的子树内,有多少个玩家 $i$ 满足 d - dep[t] = a。
有了以上两个桶,就可以在 dfs() 过程中计算答案了。
我们怎么得到仅在 $u$ 的子树 $R_u$ 内的桶信息?
还是和上一题一样,在 dfs(u) 之前,和 dfs(u) 结束后,将桶内的值 做一个减法 就可以了!
但是我们还有一个问题没解决:
我们并没有保证 $u$ 在 $s \rightarrow x \rightarrow t$ 的路径上!
这样我们多算了很多答案。为了解决这个问题,我们会发现,当我们的 dfs(u) 只要离开了 $LCA(s,t) = x$ 的子树,$x$ 节点上的信息都没用了。
所以,我们提前记录每一个节点 $u$ 作为 $LCA$ 时,$s,t$ 在桶内的信息。
可以在 dfs(u) 离开 $u$ 的时候,减去所有满足 $LCA(s,t) = u$ 的路径 $(s,t)$ 的信息。对应下面的代码是:
void dfs2(int u, int p) {
/// Other logics
////
// 从两个桶内减去 以u为LCA,(s,t)的桶信息
for (pii a : con[u]) {
ds[a.first]--;
dt[a.second]--;
}
}
... // 其他代码
int main() {
for (int i = 1; i <= m; i++) {
int s,t; cin >> s >> t;
int x = LCA(s,t);
//// Other logics
// 预处理出 以 x为LCA, s和t的桶信息
con[x].push_back({dep[s], d - dep[t]});
}
}
我们还剩最后一个问题。如果 $u$ 刚好等于 $LCA(s,t)$,且 $dep[s] - dep[u] = w_u$。
那么 $s$ 会对 $u$ 产生一次贡献,$t$ 也会产生一次贡献。多产生了一次贡献。
所以,我们预先看一下每一个玩家 $(s_i, t_i)$,它们的 $LCA$ 是否满足这个条件,如果满足,就事先将 ans[x]--;
总结一下本题:
- 将路径分为上行,下行两种。维护两个桶。
dfs()时,对于dfs()前后的信息,相减来获得子树信息。- 预处理 $LCA$ 为 $u$ 的所有贡献,在
dfs()离开 $u$ 时,从桶中减去这些贡献。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5;
int n,m,head[maxn],ecnt = 1, w[maxn], dep[maxn], par[maxn][20], ans[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int jump(int u, int d) {
for (int j = 0; j <= 19; j++) {
if (d&(1<<j)) u = par[u][j];
}
return u;
}
int LCA(int u, int v) {
if (dep[u] < dep[v]) swap(u,v);
u = jump(u, dep[u]-dep[v]);
if (u == v) return u;
for (int j = 19; j >= 0; j--) {
if (par[u][j] != par[v][j])
u = par[u][j], v = par[v][j];
}
return par[u][0];
}
void dfs(int u, int p) {
par[u][0] = p;
for (int j = 1; j <= 19; j++) par[u][j] = par[par[u][j-1]][j-1];
dep[u] = dep[p] + 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
}
}
int ds[maxn]; // 第一个桶
map<int,int> dt; // 第二个桶
int st[maxn]; // 记录 start 的数量(st[u] 代表以u为起点的路径数量)
vector<int> ed[maxn]; // ed[t] 代表以 t 为终点的所有路径的 d - dep[t] 信息
vector<pii> con[maxn];
void dfs2(int u, int p) {
int pds;
if (dep[u] + w[u] < maxn) pds = ds[dep[u] + w[u]]; // dfs前,桶1的值
else pds = 0;
int pdt = dt[-dep[u] + w[u]]; // dfs前,桶2的值
ds[dep[u]] += st[u];
for (int a : ed[u]) dt[a]++;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs2(to, u);
}
if (dep[u] + w[u] < maxn) {
ans[u] += ds[dep[u] + w[u]] - pds; // dfs后,桶1的值
}
ans[u] += dt[-dep[u] + w[u]] - pdt; // dfs后,桶2的值
for (pii a : con[u]) { // 从两个桶内减去所有 以u为LCA,(s,t)的桶信息
ds[a.first]--;
dt[a.second]--;
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
for (int i = 1; i <= n; i++) cin >> w[i];
dfs(1, 0);
for (int i = 1; i <= m; i++) {
int s,t;
cin >> s >> t;
int x = LCA(s,t);
int d = dep[s] + dep[t] - 2 * dep[x];
if (dep[s] - dep[x] == w[x]) ans[x]--; // 去重
st[s]++;
ed[t].push_back(d - dep[t]);
con[x].push_back({dep[s], d - dep[t]}); // 预处理出 以 x为LCA, s和t的桶信息
}
dfs2(1, 0);
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << endl;
}
例5 LOJ146 DFS序3 树上差分1
题意
给定有 $N$ 个节点的树,根节点为 $R$。每个节点 $i$ 具有初始权值 $V_i$。
给定 $M$ 个操作,有三种:
$1 ~ a ~ b ~ x$:将 $a,b$ 之间的路径上所有节点权值加上 $x$。(链修改)
$2 ~ a$:求节点 $a$ 的权值。(点查询)
$3 ~ a$:求节点 $a$ 子树的权值和。(子树查询)
其中,$1 \leq N,M \leq 10^6$。
题解
看起来是树链剖分的模版题,但是 $O(n\log^2n)$ 是过不了的。
本题可以利用 DFS序 + 树上差分 达到 $O(n\log n)$ 的复杂度!
首先,对于一个链 $(u,v)$,常见套路就是树上差分:
令 $x = LCA(u,v)$。
令 $f_u$ 为 从 $root$ 到 $u$ 的路径上,被加上了多少。
令 $val$ 为本次修改的值。
然后链修改就被转化为 $f_u+val, f_v + val, f_x - val, f_{par(x)} - val$ 了。
现在问题是,有了 $f_u$ 的值,怎么查询?
在树上差分中,一个很常见的套路是 贡献 思想。
对于每一个修改,我们都考虑,它对哪些节点的查询具有贡献?
注意到 $f_u$ 是从 $root$ 到 $u$ 的路径上,被修改的值。
对于单点查询 $a$,我们可以发现:
只要 $u$ 在 $a$ 的子树内,那么 $f_u$ 就可以被加到 $a$ 上,作为 $u$ 对 $a$ 的贡献。
所以,单点查询 $a$ 就变成了:
求 $a$ 的子树中的所有节点 $u$ 的 $f_u$ 之和。
$$ans = \sum\limits_u f_u$$
拿线段树维护一下子树中,$f_u$ 的 sum 即可。
对于子树查询 $a$,可以发现:
当我们修改 $f_u$ 的时候,如果 $u$ 在 $a$ 的子树内,那么从 $a$ 到 $u$ 的这一条链上所有的节点,都应该被算入贡献当中。
而这个贡献,刚好就是 $(d_u - d_a + 1) \times f_u$。($d_u$ 为 $u$ 的depth)
但是,我们不能直接把 $(d_u - d_a + 1) \times f_u$ 加到 $a$ 上面,因为 $a$ 的子树中,每个节点的depth不相同。
$$ans = \sum\limits_u (d_u - d_a + 1) \times f_u = \sum\limits_u d_uf_u + (1-d_a)\sum\limits_u f_u$$
所以,线段树还需要再维护一下子树中,$d_uf_u$ 的 sum。
最后注意一下,每个节点有个初始的权值 $V_i$,这个拿一个 sum[] 数组单独维护一下就行,每次查询的时候记得加上。
本题卡常,一些卡常小技巧:
- 使用树链剖分来求 $LCA$,复杂度仍然是 $O(\log n)$,但是常数小。
- 线段树query的时候,使用传入sum的reference,来进行查询。这样就不用返回查询值了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int n, m, root, in[maxn], out[maxn], par[maxn], idcnt = 0, ecnt = 1, head[maxn], V[maxn];
ll sum[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int top[maxn], son[maxn], dep[maxn];
void dfs(int u, int p) {
sum[u] += (ll)(V[u]);
in[u] = ++idcnt;
par[u] = p;
dep[u] = dep[p] + 1;
int maxsz = -1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
int sz = out[to] - in[to] + 1;
if (sz > maxsz) {
maxsz = sz;
son[u] = to;
}
sum[u] += sum[to];
}
out[u] = idcnt;
}
void dfs2(int u, int p, int topf) {
top[u] = topf;
if (son[u]) dfs2(son[u], u, topf);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p || to == son[u]) continue;
dfs2(to, u, to);
}
}
int LCA(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
u = par[top[u]];
}
if (dep[u] < dep[v]) return u;
return v;
}
struct tree_node {
ll fsum, dfsum;
} tr[maxn<<2];
void update(int cur, int l, int r, int p, int val1, ll val2) {
tr[cur].fsum += (ll)val1;
tr[cur].dfsum += val2;
if (l == r) return;
int mid = (l+r) >> 1;
if (p <= mid) update(cur<<1, l, mid, p, val1, val2);
else update(cur<<1|1, mid+1, r, p, val1, val2);
}
void query(int cur, int l, int r, int L, int R, ll& fsum, ll& dfsum) {
if (l >= L && r <= R) {
fsum += (ll)(tr[cur].fsum);
dfsum += (ll)(tr[cur].dfsum);
return;
}
int mid = (l+r) >> 1;
if (L <= mid) query(cur<<1, l, mid, L, R, fsum, dfsum);
if (R > mid) query(cur<<1|1, mid+1, r, L, R, fsum, dfsum);
}
int main() {
read(n); read(m); read(root);
for (int i = 1; i <= n; i++) read(V[i]);
for (int i = 1; i <= n-1; i++) {
int u,v; read(u); read(v);
addEdge(u, v); addEdge(v, u);
}
dfs(root, 0);
dfs2(root, 0, root);
while (m--) {
int op; read(op);
if (op == 1) {
int a,b,x; read(a); read(b); read(x);
int lca = LCA(a,b), p = par[lca];
update(1, 1, n, in[a], x, (ll)(dep[a]) * (ll)(x));
update(1, 1, n, in[b], x, (ll)(dep[b]) * (ll)(x));
update(1, 1, n, in[lca], -x, -(ll)(dep[lca]) * (ll)(x));
update(1, 1, n, in[p], -x, -(ll)(dep[p]) * (ll)(x));
} else if (op == 2) {
int a; read(a);
int L = in[a], R = out[a];
ll fsum = 0, dfsum = 0;
query(1, 1, n, L, R, fsum, dfsum);
fsum += (ll)(V[a]);
write(fsum);
} else {
int a; read(a);
ll fsum = 0, dfsum = 0;
int L = in[a], R = out[a];
query(1, 1, n, L, R, fsum, dfsum);
ll res = dfsum;
ll d = dep[a];
res += (1LL - d) * fsum;
res += sum[a];
write(res);
}
}
}
例6 LOJ147 DFS序4
题意
给定有 $N$ 个节点的树,根节点为 $R$。每个节点 $i$ 具有初始权值 $V_i$。
给定 $M$ 个操作,有三种:
$1 ~ a ~ x$:将节点 $a$ 的权值加上 $x$。(点修改)
$2 ~ a ~ x$:将节点 $a$ 的子树中,所有节点权值加上 $x$。(子树修改)
$3 ~ a ~ b$:求 $a,b$ 之间的路径上所有节点权值和。(链查询)
其中,$1 \leq N,M \leq 10^6$。
题解
和上一题思路几乎一致,仍然是考虑每个修改,对于查询的贡献。
主要的原因在于 链 是只能通过 $f_u$ 来维护的。
考虑 单点修改 $a$ 对于 $f_u$ 的贡献?
如果 $u$ 在 $a$ 的子树内,则 单点修改 $a$ 对于 $f_u$ 具有贡献 $val$。
所以单点修改 $a$,就变成了:
将 $a$ 的子树内,所有的 $f_u$ 加上 $val$。
考虑 修改 $a$ 的子树 对于 $f_u$ 的贡献?
如果 $u$ 在 $a$ 的子树内,则修改 $a$ 的子树 对于 $f_u$ 具有贡献 $(d_u - d_a + 1) \times val$
所以单点修改 $a$,就变成了:
将 $a$ 的子树内,所有的 $f_u$ 加上 $(d_u - d_a + 1) \times val$。
然而由于 $d_u$ 对于每个 $u$ 均不同,拆开的话就是:
$$d_u \times val + (1-d_a) \times val$$
对于 $d_u \times val$,我们直接维护 $val$ 的 sum,在询问的时候再把 $d_u$ 乘上去。
对于 $(1-d_a) \times val$,我们直接加到 $f_u$ 上即可。
所以,在线段树中,我们维护两个值,$f_u$ 和 $g_u$。
单点修改 $a$ 的时候,将 $a$ 的子树内,所有的 $f_u$ 加上 $val$。
修改 $a$ 的子树时,将 $a$ 的子树内,所有的 $f_u$ 加上 $(1-d_a) \times val$,所有的 $g_u$ 加上 $val$。
查询 $f_u$ 的真正值 $ans$ 时,有:
$$ans = f_u + d_u g_u$$
对于每个节点的初始值 $V_i$,仍然用一个 sum[] 数组单独维护一下,查询的时候记得加上。
注:线段树在 push_down() 和 update(L,R) 的时候,记得要考虑到当前节点的区间长度 len = (r-l+1)。
总结:
例5和例6是 DFS序+树上差分+贡献思想 的优秀应用。
但是这样的做法局限性比较强,仅适用于一些特殊情况。
- 链修改 + 点/子树查询
- 链查询 + 点/子树修改
上面这两种可以这样做。但是如果有 链修改 + 链查询 就必须用树链剖分来做了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int n, m, root, in[maxn], out[maxn], par[maxn], idcnt = 0, ecnt = 1, head[maxn], V[maxn];
ll sum[maxn]; // sum[u] 代表 root -> u 的链sum
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int top[maxn], son[maxn], dep[maxn];
void dfs(int u, int p) {
sum[u] += (ll)(V[u]);
in[u] = ++idcnt;
par[u] = p;
dep[u] = dep[p] + 1;
int maxsz = -1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
sum[to] += sum[u];
dfs(to, u);
int sz = out[to] - in[to] + 1;
if (sz > maxsz) {
maxsz = sz;
son[u] = to;
}
}
out[u] = idcnt;
}
void dfs2(int u, int p, int topf) {
top[u] = topf;
if (son[u]) dfs2(son[u], u, topf);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p || to == son[u]) continue;
dfs2(to, u, to);
}
}
int LCA(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u,v);
u = par[top[u]];
}
if (dep[u] < dep[v]) return u;
return v;
}
struct tree_node {
ll fsum, dfsum;
bool lazy = 0;
ll lazy_fsum, lazy_dfsum;
} tr[maxn<<2];
void push_down(int cur, int L, int R) {
if (!tr[cur].lazy) return;
ll lazy_fsum = tr[cur].lazy_fsum, lazy_dfsum = tr[cur].lazy_dfsum;
tr[cur].lazy = 0;
tr[cur].lazy_fsum = tr[cur].lazy_dfsum = 0;
int l = cur<<1, r = l|1;
tr[l].lazy = 1, tr[r].lazy = 1;
tr[l].lazy_fsum += lazy_fsum; tr[r].lazy_fsum += lazy_fsum;
tr[l].lazy_dfsum += lazy_dfsum; tr[r].lazy_dfsum += lazy_dfsum;
int mid = (L+R) >> 1;
ll llen = (mid-L+1), rlen = (R-mid); // 记得这里有 len
tr[l].fsum += llen * lazy_fsum, tr[r].fsum += rlen * lazy_fsum;
tr[l].dfsum += llen * lazy_dfsum, tr[r].dfsum += rlen * lazy_dfsum;
}
void push_up(int cur) {
tr[cur].fsum = tr[cur<<1].fsum + tr[cur<<1|1].fsum;
tr[cur].dfsum = tr[cur<<1].dfsum + tr[cur<<1|1].dfsum;
}
void update(int cur, int l, int r, int L, int R, ll val1, ll val2) {
if (l >= L && r <= R) {
ll len = (r-l+1); // 记得这里有 len
tr[cur].fsum += len * val1;
tr[cur].dfsum += len * val2;
tr[cur].lazy_fsum += val1;
tr[cur].lazy_dfsum += val2;
tr[cur].lazy = 1;
return;
}
push_down(cur, l, r);
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, val1, val2);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, val1, val2);
push_up(cur);
}
void query(int cur, int l, int r, int L, int R, ll& fsum, ll& dfsum) {
if (l >= L && r <= R) {
fsum += (ll)(tr[cur].fsum);
dfsum += (ll)(tr[cur].dfsum);
return;
}
push_down(cur, l, r);
int mid = (l+r) >> 1;
if (L <= mid) query(cur<<1, l, mid, L, R, fsum, dfsum);
if (R > mid) query(cur<<1|1, mid+1, r, L, R, fsum, dfsum);
}
// get the result of vertex u
ll get_res(int u) {
if (!u) return 0;
ll fsum = 0, dfsum = 0;
query(1, 1, n, in[u], in[u], fsum, dfsum);
ll res = fsum + (ll)(dep[u]) * dfsum + sum[u];
return res;
}
int main() {
read(n); read(m); read(root);
for (int i = 1; i <= n; i++) read(V[i]);
for (int i = 1; i <= n-1; i++) {
int u,v; read(u); read(v);
addEdge(u, v); addEdge(v, u);
}
dfs(root, 0);
dfs2(root, 0, root);
while (m--) {
int op; read(op);
if (op == 1) {
int a,x; read(a); read(x);
update(1, 1, n, in[a], out[a], x, 0);
} else if (op == 2) {
int a,x; read(a); read(x);
ll fsum = (ll)(1-dep[a]) * (ll)(x);
update(1, 1, n, in[a], out[a], fsum, x);
} else {
int a,b; read(a); read(b);
int lca = LCA(a,b), p = par[lca];
ll r1 = get_res(a), r2 = get_res(b), r3 = get_res(lca), r4 = get_res(p);
ll res = r1+r2-r3-r4;
write(res);
}
}
}