割点桥点/边双连通分量（BCC）

定义

割点

在一个 无向图 中，如果删掉节点 $u$ 使得整个图的连通分量增加，那么 $u$ 是一个割点。

桥

在一个 无向图 中，如果删掉一条边 $(u,v)$ 使得整个图的连通分量增加，那么 $(u,v)$ 是一个桥。

点双连通

一个 无向图 是 点双连通 的，当且仅当（以下表达是 equivalent 的）：

如果删去任意一个节点，其他节点仍然互相连通。
不包含割点（注意，这个割点是对于 这个子图 而言）。
任取两个点 $u,v$，$u,v$ 之间都存在两条 点不重复 路径。
任取 $2$ 条边，都存在一个简单环（环内不包含其他环），使得这 $2$ 条边在这个简单环内。

• 注意，如果图内只有 $2$ 个连起来的节点，它们仍然点双连通。

• 点双连通 不具有传递性：

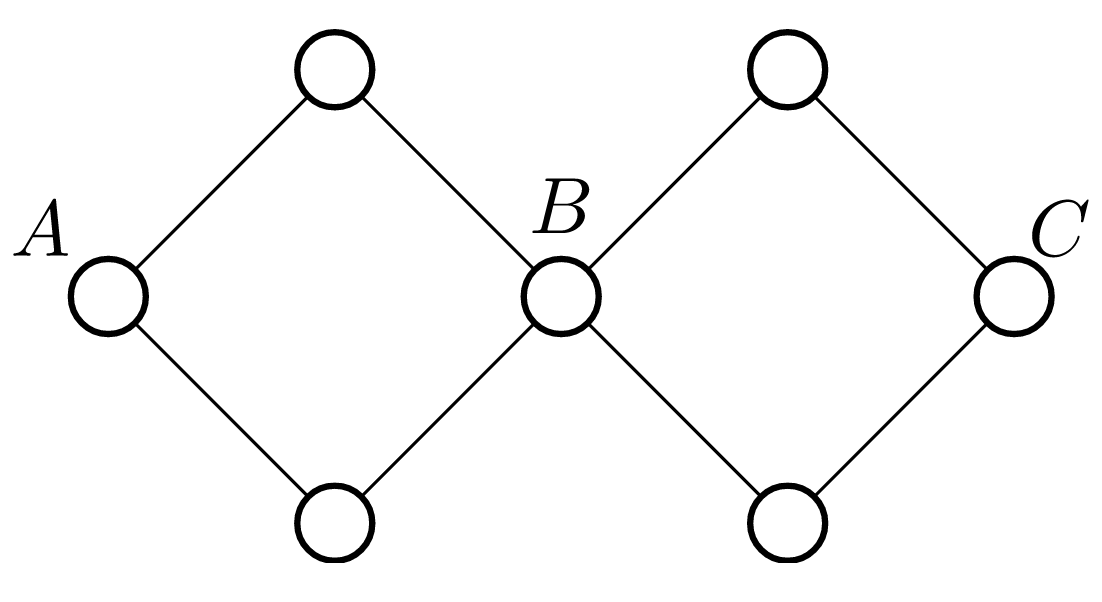
如上图，$a,b$ 点双连通，$b,c$ 点双连通，但是 $a,c$ 并不点双连通（$a,c$ 不在同一个点双分量内）。

边双连通

一个 无向图 是 边双连通 的，当且仅当（以下表达是 equivalent 的）：

一个 无向图 中，如果删去任意一条边，其他节点仍然互相连通。
一个 无向图 中，不包含桥（注意，这个桥是对于 整个图 而言）。
一个 无向图 中，任取两个点 $u,v$，$u,v$ 之间都存在两条 边不重复 路径。
一个 无向图 中，任取 $1$ 条边，都存在一个简单环（环内不包含其他环），使得这条边在这个简单环内。

• 点双连通 具有传递性：

如果 $a,b$ 边双连通，$b,c$ 边双连通，则 $a,c$ 边双连通。

证明：$a,b$ 边双连通说明删去图中任意一条边，$a,b$ 仍连通。同理，删去图中任意一条边，$b,c$ 仍连通。所以删去任意一条边，$a,c$ 仍连通。

点双连通分量

点双连通分量：一个极大的点双连通的子图。

如果把这个子图 单独拿出来，它不存在割点，但是它在原图中，如果它与其他点双分量相连，那么它一定包含至少一个原图中的割点。
原图中，每个割点 存在于至少 $2$ 个点双分量中。
任意一个 非割点 只存在于一个点双分量中。

点双缩点

利用点双缩点后，得到的新图有以下性质：

新图 是一棵树，每个节点要么是一个点双，要么是一个割点。
所有割点单独成为一个节点。
点双之间以割点相连，并且所有割点的 degree 至少为 $2$。（任意两个点双之间，有且仅有一个公共点，且这个公共点是割点）。

例1：

图中的所有点双分量为：$\{1,2,3\}, \{3,4,5\}$

图中所有割点为：$3$

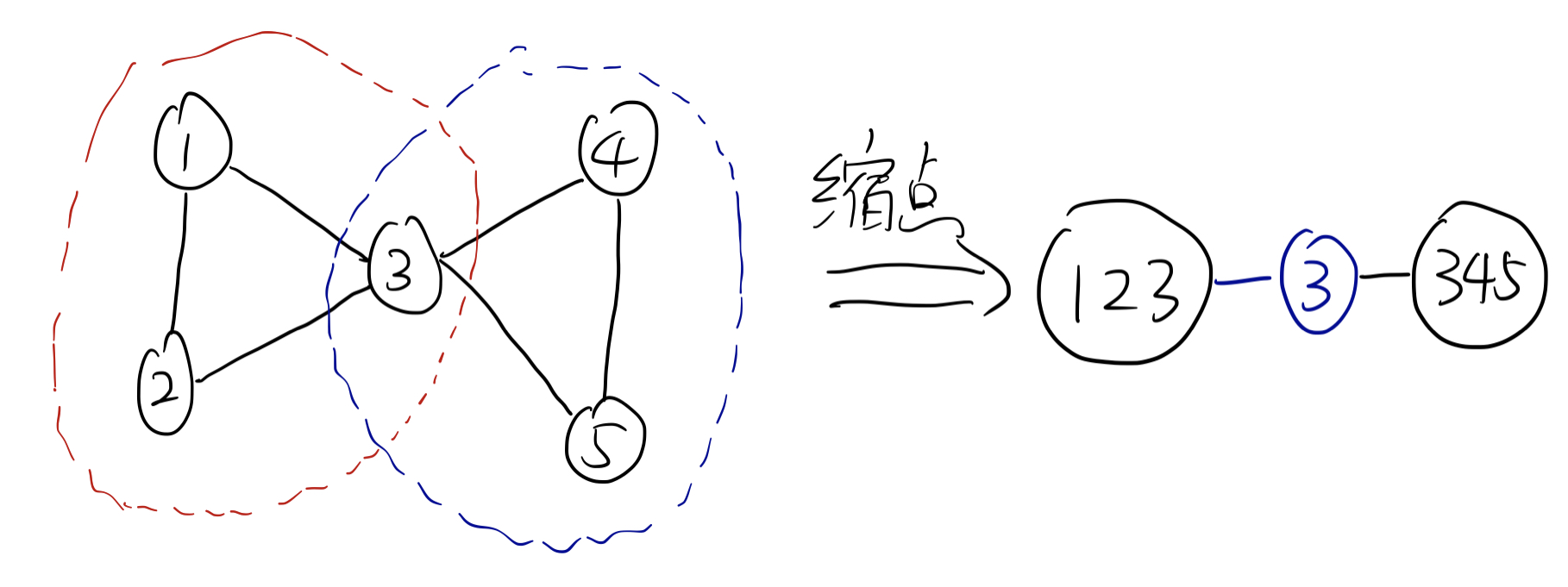
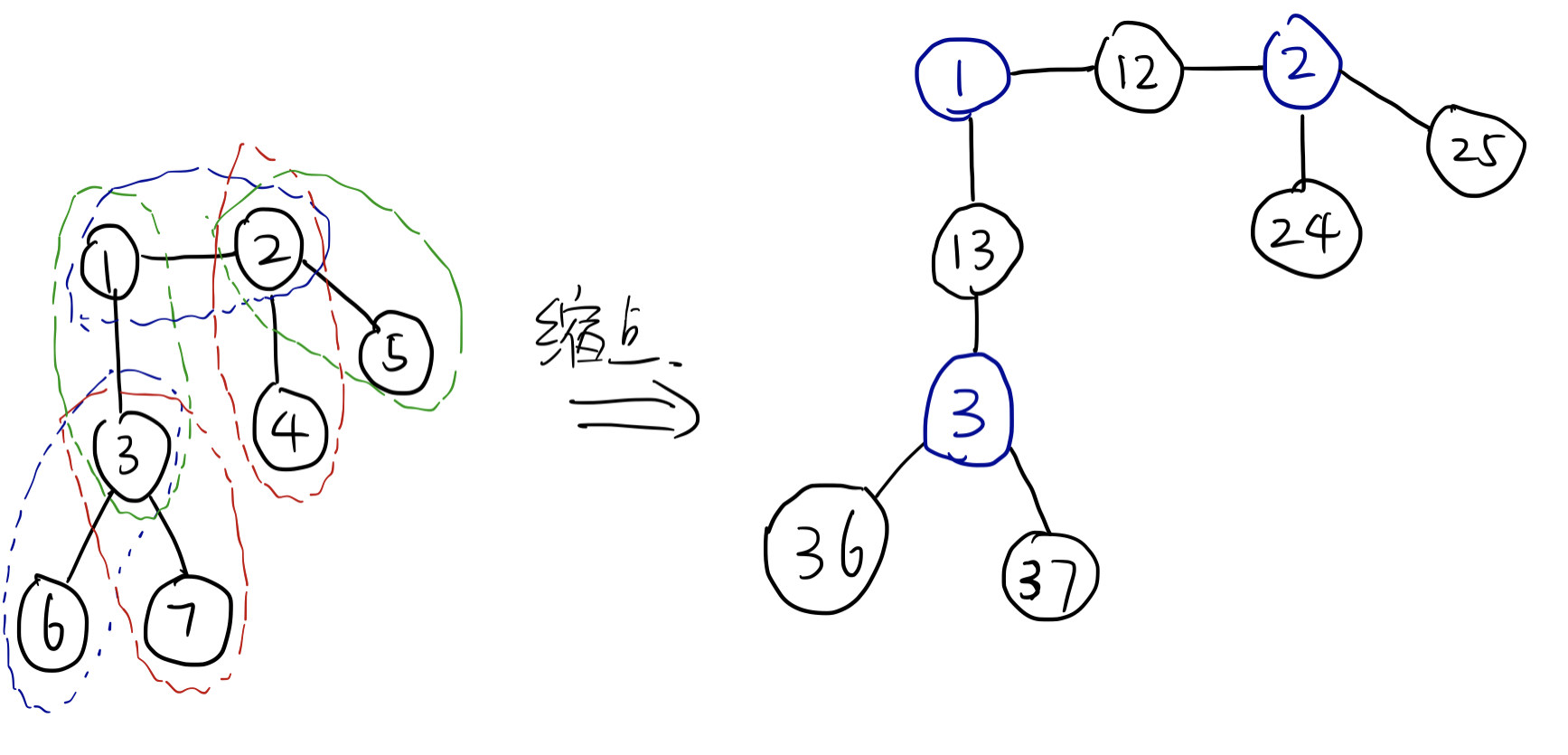
例2：

图中的所有点双分量为：$\{1,2\}, \{1,3\}, \{2,4\}, \{2,5\}, \{3,6\}, \{3,7\}$

图中所有割点为：$1,2,3$

边双连通分量

边双连通分量：一个极大的边双连通子图。

相比点双分量来说，边双分量的定义简单很多，因为它 不需要区分 原图和子图！

将原图中的所有桥删掉，剩下的分量就是边双连通分量。
桥不属于任何一个边双分量，边双分量之间以桥连接。

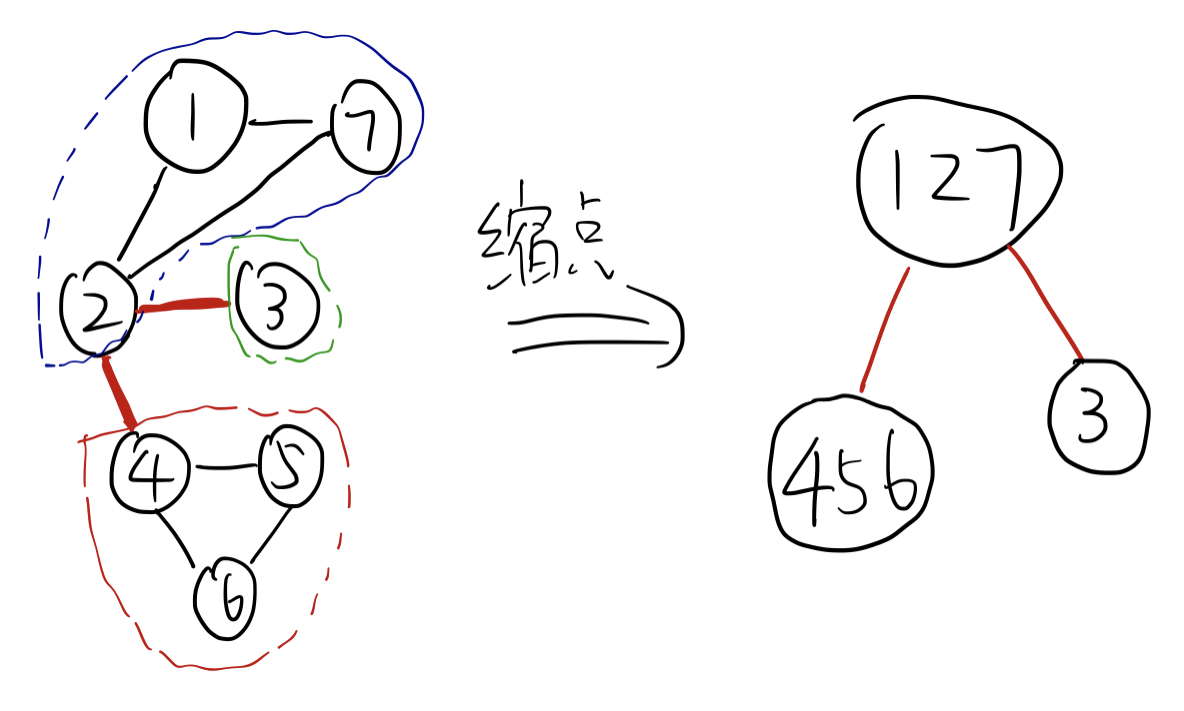
例1：

图中的所有边双分量为：$\{1,2,7\}, \{4,5,6\}, \{3\}$

图中所有桥为：$(2,3), (2,4)$

边双缩点

利用边双缩点后，得到的新图有以下性质：

新图是 一棵树，每个节点都是一个边双。
原图中 所有的桥，在新图中仍然是桥。

算法

我们利用 tarjan 算法求 割点，桥，点双，边双。

这里的 tarjan 和有向图求SCC 的tarjan略有不同，主要体现在：

有向图tarjan求SCC：需要记录当前在栈内的有哪些元素，更新 low[] 时，需要 to 在栈内才更新。
无向图求割点/桥/点双/边双：需要检查 to 是不是 u 的直接 parent p。（这里指的是 dfs树内的parent关系），不需要考虑是否在栈内。

另外，求 割点和桥 时，也略有不同，主要体现在：

求割点时，需要讨论当前节点是否为DFS树的根。但是求桥时，不需要。
求割点时，条件是 $low[to] \geq dfn[u]$。求桥时，条件是 $low[to] > dfn[u]$。

以下的算法，都要检查 to 是不是 u 的直接 parent p。

割点

对于一个节点 $u$，在DFS树中，如果：

它是DFS树的 根节点：如果 $u$ 拥有 $\geq 2$ 个子树，那么 $u$ 就是一个割点。
它不是DFS树的根节点：如果 $u$ 存在一个 direct child $~to$，使得 $low[to] \geq dfn[u]$。那么 $u$ 就是一个割点。（因为这说明 $to$ 无法到达 $u$ 的上方）

模版题

题意

给定一个无向图，求图的所有割点。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e4+5;
const int maxm = 1e5+10;

struct Edge {
    int to, nxt;
} edges[maxm<<1];

int dfn[maxn], low[maxn], head[maxn], ecnt = 1, n, m, id;
void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}
vector<int> ans;

void dfs(int u, int p) {
    dfn[u] = ++id;
    low[u] = id;
    int child = 0;  // 子树数量
    bool cut = 0;  // 是否为割点
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;  // 不能直接用parent

        if (dfn[to]) {
            low[u] = min(low[u], dfn[to]);
            continue;
        }

        dfs(to, u);
        child++;
        low[u] = min(low[u], low[to]);
        if (p && low[to] >= dfn[u]) cut = 1;  
        // 如果u不是根节点，且存在 direct child使得 low[to] >= dfn[u]，则u是割点
    }
    if (!p && child >= 2) cut = 1;  // 如果为根节点，且有 >= 2个子树
    if (cut) ans.push_back(u);
}

void tarjan() {
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) dfs(i, 0);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        addEdge(u,v); addEdge(v,u);
    }
    tarjan();

    sort(ans.begin(), ans.end());
    cout << ans.size() << endl;
    for (int a : ans) cout << a << " ";
    cout << endl;
}

桥

判断一个边 $(u,to)$ 是不是桥，我们设 $u$ 在DFS树中，是 $to$ 的parent。

如果 $low[to] > dfn[u]$，则 $(u,to)$ 是一个桥。（因为这说明 $to$ 无法到达 $u$ 和 $u$ 的上方）。

实现过程中，需要注意以下几点：

边的编号从 $0$ 开始（记得将 head[] 初始化为 -1），这样保证了 e 和 e^1 刚好为 $(u,v)$ 和 $(v,u)$。
标记桥的时候，一次标记两个边 e 和 e^1。

代码

void tarjan(int u, int p) {
    dfn[u] = low[u] = ++id;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;  // 注意不能用parent
        if (dfn[to]) low[u] = min(low[u], dfn[to]);
        else {
            tarjan(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] > dfn[u]) {  // 注意这里的条件
                bridge[e] = bridge[e^1] = 1;
            }
        }
    }
}

点双连通分量（dcc）

求点双分量，可以在求割点的时候顺便求出来。

当我们发现 $low[to] \geq dfn[u]$ 时，就说明 $to$ 及其子树（加上 $u$）一起形成了一个点双。

此时，我们将栈内的点一直pop，pop 到 to 为止（包括 to），但是 不包括 u。这是因为 u 作为割点，可能还属于别的点双分量，之后还要用到。

• 求点双时，我们并不关心 $u$ 本身是否为割点，只要出现了 $low[to] \geq dfn[u]$，就说明出现了一个新点双。（例如，在只有 $1,2$ 这两个点的情况下，不存在割点，但是 $1,2$ 仍然是一个点双）。

代码

int dfn[maxn], low[maxn], id, st[maxn], tail = -1, from[maxn], dcc;
bool cut[maxn];
vector<int> dcc_list[maxn];
void dfs(int u, int p) {
    dfn[u] = low[u] = ++id;
    st[++tail] = u;
    int child = 0;

    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) {
            low[u] = min(low[u], dfn[to]);
        } else {
            child++;
            dfs(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] >= dfn[u]) {
                from[to] = ++dcc;
                while (st[tail] != to) {  // 注意是 pop 到 to 为止（包括to）
                    int cur = st[tail--];
                    from[cur] = from[to];
                    dcc_list[dcc].push_back(cur);
                }
                tail--;  // tail--后，指向的是 u
                dcc_list[dcc].push_back(to);
                dcc_list[dcc].push_back(u);  // 注意 u是割点，也要进入该分量
                // from[u] = dcc;  // from[u] 实际上没有意义
            }
            if (low[to] >= dfn[u] && p) cut[u] = 1;  // 割点（非根节点）
        }
    }
    if (!p && child >= 2) cut[u] = 1;  // 割点（根节点）
}

void tarjan() {
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) dfs(i, 0);
    }
}

void rebuild() {
    for (int i = 1; i <= dcc; i++) {
        for (int j : dcc_list[i]) {
            if (cut[j]) cut_from[j].push_back(i);
        }
    }
    for (int u = 1; u <= n; u++) {
        if (cut[u]) {
            int fu = from[u] = ++dcc;
            mp[dcc] = u;
            dcc_list[dcc].push_back(u);
            for (int fv : cut_from[u]) {
                adj[fu].push_back(fv);
                adj[fv].push_back(fu);
            }
        }
    }
}

边双连通分量（ecc）

求边双分量，可以根据定义：删去所有的桥，剩下的连通分量，就是边双分量。

所以求边双分量，分以下两步：

tarjan 求出所有的桥。
进行一次 dfs()，如果 $(u,to)$ 是桥，则不经过这条边。以此求出所有的连通分量。

代码

int n,m, head[maxn], ecnt = 0, dfn[maxn], low[maxn], id = 0, from[maxn], ecc = 0;
bool bridge[maxm<<1];
struct Edge {
    int to, nxt;
} edges[maxm<<1];
void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}
void tarjan(int u, int p) {
    dfn[u] = low[u] = ++id;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) low[u] = min(low[u], dfn[to]);
        else {
            tarjan(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] > dfn[u]) {
                bridge[e] = bridge[e^1] = 1;
            }
        }
    }
}
// f 代表 from (ecc编号)
void dfs(int u, int f) {
    from[u] = f;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (from[to] || bridge[e]) continue;  // to已访问，或者该边是桥
        dfs(to, f);
    }
}
vector<int> adj[maxn];
void rebuild() {
    for (int u = 1; u <= n; u++) {
        for (int e = head[u]; ~e; e = edges[e].nxt) {
            int v = edges[e].to;
            int fu = from[u], fv = from[v];
            if (fu == fv) continue;
            adj[fu].push_back(fv);
        }
    }
}

int main() {
    // ...
    tarjan(1, 0);
    for (int i = 1; i <= n; i++) 
        if (!from[i]) 
            dfs(i, ++ecc);
    rebuild();
    // ...
}

例题

例1 洛谷P3225 [HNOI2012]矿场搭建

题意

给定 $M$ 条边的无向图。初始状态下，每个节点没有标记。

我们需要给节点打上标记，使得：

删去图中的任意一个节点，其他的所有节点均可到达一个有标记的节点。

求：标记节点的最少数量，最少标记数量的方案总数。

其中，$M \leq 500$，数据保证不存在单个独立点。

题解

首先根据 点双连通 进行缩点。缩点以后，整个图会变成一个由割点和 点双分量 组成的树。

由于点双的性质，我们知道，如果删去点双分量中的任意一个点（除割点以外），该分量仍然和其他的分量连通。

所以我们不需要考虑删去 非割点 的情况，我们只关心如果删去了一个割点，会不会使得有些节点无法到达有标记的节点。

由上可知，我们 不需要标记割点（因为我们只考虑删去割点的情况，如果要删去割点，那说明标记割点是无意义的）。

对于一个点双分量而言，可以分以下情况讨论：

点双内含有 $\geq 2$ 个割点：无论删去哪个割点，该分量仍然和其他分量连通，所以无需在该分量内标记。
点双内含有 $1$ 个割点：如果该割点被删了，那么这个分量就断开了，所以该分量内部需要标记 $1$ 个节点。（不标记割点），方案数为 $(sz-1)$ （因为分量里面有一个割点，要去掉标记它的可能性）。
点双内没有割点：说明这个分量本来就是独立开的（在缩点后，是单个独立节点）。所以该分量内需要标记 $2$ 个节点。方案数为 $C_{sz}^2$。

实现中的一些细节：

由于一个割点可能属于多个点双分量，所以我们采用 vector<int> dcc_list[maxn]; 来记录每个点双里面的节点。
对于一个割点 $u$ 来说，它的 from[] 数组没有意义。（如果需要缩点，则后续会让 from[u] = ++dcc，缩点后的 from[u] 就有意义了）
与 tarjan 求 SCC 不同，我们不需要记录节点是否在栈内。
在 pop 栈的时候，注意我们是 pop 到 to 为止（包括 to），但是 不包括 u。这是因为 u 作为割点，可能还属于别的点双分量，之后还要用到。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;

int n,m, head[maxn], ecnt = 1;
struct Edge {
    int to, nxt;
} edges[maxn];
void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}

int dfn[maxn], low[maxn], id, st[maxn], tail = -1, from[maxn], dcc;
bool cut[maxn];
vector<int> dcc_list[maxn];
void dfs(int u, int p) {
    dfn[u] = low[u] = ++id;
    st[++tail] = u;
    int child = 0;

    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) {
            low[u] = min(low[u], dfn[to]);
        } else {
            child++;
            dfs(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] >= dfn[u]) {
                from[to] = ++dcc;
                while (st[tail] != to) {  // 注意是 pop 到 to 为止（包括to）
                    int cur = st[tail--];
                    from[cur] = from[to];
                    dcc_list[dcc].push_back(cur);
                }
                tail--;  // tail--后，指向的是 u
                dcc_list[dcc].push_back(to);
                dcc_list[dcc].push_back(u);  // 注意 u是割点，也要进入该分量
                // from[u] = dcc;  // from[u] 实际上没有意义
            }
            if (low[to] >= dfn[u] && p) cut[u] = 1;  // 割点（非根节点）
        }
    }
    if (!p && child >= 2) cut[u] = 1;  // 割点（根节点）
}

void tarjan() {
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) dfs(i, 0);
    }
}

void init() {
    for (int i = 1; i <= dcc; i++) dcc_list[i].clear();
    id = 0;
    tail = -1;
    dcc = 0;
    n = 0;
    ecnt = 1;

    fill(cut, cut+maxn, 0);
    fill(from, from+maxn, 0);
    fill(head, head+maxn, 0);
    fill(dfn, dfn+maxn, 0);
    fill(low, low+maxn, 0);
}

void solve(int T) {
    init();
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        n = max(n,u); n = max(n,v);
        addEdge(u,v); addEdge(v,u);
    }
    tarjan();

    int ans1 = 0;
    ll ans2 = 1;

    for (int i = 1; i <= dcc; i++) {
        int cut_cnt = 0;
        int sz = dcc_list[i].size();
        for (int j = 0; j < dcc_list[i].size(); j++) {
            int cur = dcc_list[i][j];
            if (cut[cur]) cut_cnt++;
        }
        if (cut_cnt >= 2) continue;
        if (cut_cnt == 1) ans1++, ans2 *= (ll)(sz - 1);
        if (cut_cnt == 0) ans1+=2, ans2 *= (ll)(sz) * (ll)(sz-1LL) / 2LL;
    }

    printf("Case %d: %d %lld\n", T, max(ans1, 2), ans2);
}

int main() {
    int T = 0;
    while (cin >> m && m) {
        T++;
        solve(T);
    }
}

例2 洛谷P5058 [ZJOI2004]嗅探器

题意

现有 $n$ 个节点的无向图。

给定两个节点 $a,b$，输出最小编号的 $u$ 使得 $a,b$ 之间所有的路径都需要经过 $u$，且 $u \neq a, u \neq b$。

如果无解，则输出 “No solution”。

题解

先点双缩点，如果 $a,b$ 在同一个点双内必然无解（根据定义，大小等于 $3$ 的点双内，任意两点之间有点不重复的路径）。

如果 $a,b$ 在不同的点双内则说明有解，缩点后，$a,b$ 就是树上的两个节点，它们之间有唯一路径，取这个路径上编号最小的割点即可。

一些注意事项：

每个割点单独形成一个点双。
缩点得到的树，所有的边必然和割点相连，所以建边的时候只需要考虑割点所在的dcc，还有它旁边有哪些dcc就可以了。本题中在缩点建树的过程中，使用了数组 vector<int> cut_from[maxn];。其中 cut_from[u] 代表以 $u$ 作为割点，它neighbor的dcc编号。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
const int maxm = 5e5+5;

int n,a,b,head[maxn],ecnt = 0;
struct Edge {
    int to, nxt;
} edges[maxm<<1];

void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

int dfn[maxn], low[maxn], dcc = 0, id = 0, st[maxn], from[maxn], tail = -1;
bool cut[maxn];
vector<int> dcc_list[maxn<<1];
vector<int> cut_from[maxn];  // cut_from[u] 代表以 u 作为割点，它neighbor的dcc编号
void tarjan(int u, int p) {
    dfn[u] = low[u] = ++id;
    st[++tail] = u;
    int child = 0;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) low[u] = min(low[u], dfn[to]);
        else {
            child++;
            tarjan(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] >= dfn[u]) {
                from[u] = ++dcc;
                while (st[tail] != to) {
                    int cur = st[tail--];
                    from[cur] = from[u];
                    dcc_list[dcc].push_back(cur);
                }
                tail--;
                from[to] = from[u];
                dcc_list[dcc].push_back(to);
                dcc_list[dcc].push_back(u);
            }

            if (low[to] >= dfn[u] && p) {
                cut[u] = 1;
            }
        }
    }
    if (child >= 2 && !p)
        cut[u] = 1;
}

vector<int> adj[maxn<<1];  // 缩点后的图
int par[maxn<<1], dep[maxn<<1];  // 缩点后，dfs树用到的数组
int mp[maxn<<1];  // map: dcc -> cut vertex id (只有该dcc对应的是 单个割点形成的 dcc才有用)

void dfs(int u, int p) {
    par[u] = p;
    dep[u] = dep[p] + 1;
    for (int to : adj[u]) {
        if (to == p) continue;
        dfs(to, u);
    }
}

int ans = 1e9;
void LCA(int u, int v) {
    int f1 = mp[u], f2 = mp[v];
    if (dep[u] < dep[v]) swap(u,v);
    int d = dep[u] - dep[v];
    vector<int> path;
    while (d--) {
        path.push_back(u);
        u = par[u];
    }
    path.push_back(u);
    while (u != v) {
        path.push_back(u);
        path.push_back(v);
        u = par[u], v = par[v];
    }
    path.push_back(u);
    path.push_back(v);
    for (int c : path) {
        if (mp[c] == f1 || mp[c] == f2) continue;
        if (cut[mp[c]]) ans = min(ans, mp[c]);
    }
}

void rebuild() {
    for (int i = 1; i <= dcc; i++) {
        for (int j : dcc_list[i]) {
            if (cut[j]) cut_from[j].push_back(i);
        }
    }

    for (int u = 1; u <= n; u++) {
        if (cut[u]) {
            int fu = from[u] = ++dcc;
            mp[dcc] = u;
            dcc_list[dcc].push_back(u);
            for (int fv : cut_from[u]) {
                adj[fu].push_back(fv);
                adj[fv].push_back(fu);
            }
        }
    }
}

int main() {
    cin >> n;
    int u,v;
    fill(head, head+maxn, -1);
    while (cin >> u >> v && u && v) {
        addEdge(u,v); addEdge(v,u);
    }
    cin >> a >> b;
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) tarjan(i,0);
    }
    rebuild();
    for (int i = 1; i <= dcc; i++) {
        if (!dep[i]) dfs(i,0);
    }
    LCA(from[a], from[b]);

    if (ans == 0 || ans == 1e9) cout << "No solution" << endl;
    else cout << ans << endl;
}

例3 POJ3694 Network

题意

给定 $N$ 个节点和 $M$ 条边的无向图，初始图是连通的。

现在要加 $Q$ 条边（可重复），每次加边后，回答图中有多少个桥。

其中，$1 \leq N \leq 10^5, N-1 \leq M \leq 2 \times 10^5, 1\leq Q \leq 1000$

题解

既然是桥，那么就直接先求一个边双，然后缩点。

边双缩点后可以得到一棵树，所有加边操作都放到这个树上来考虑。

首先会发现，加上的新边必不可能是桥（因为图原本是连通的）。

每次加边 $(u,v)$，如果 $u,v$ 在同一个边双里，那么不会有任何影响。

如果 $u,v$ 不在同一个边双里，那么加上的这条新边就会在树上形成一个环，使得环内的所有边均 不再是桥。

那么，回忆一下 AcWing 352 暗之连锁中，我们可以将树边看作主要边，新加上的边就转化为主要边。

比如，我们加上 $(u,v)$，那么就给 $u,v$ 之间路径上所有的边打一个标记。被标记过的就不是桥，没标记的就都是桥。

然而树上差分的做法只适用于离线，只有所有修改操作结束后询问才有效。

在线的做法我们可以利用 树链剖分（询问边），每次修改前，先进行一下询问，查询有多少个在修改前是无标记的，将答案减去这个数量即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 2e5+5;

int n,m, head[maxn], ecnt = 0, dfn[maxn], low[maxn], id = 0, from[maxn], ecc = 0;
bool bridge[maxm<<1];
struct Edge {
    int to, nxt;
} edges[maxm<<1];
void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}

void tarjan(int u, int p) {
    dfn[u] = low[u] = ++id;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) low[u] = min(low[u], dfn[to]);
        else {
            tarjan(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] > dfn[u]) {
                bridge[e] = bridge[e^1] = 1;
            }
        }
    }
}

// f 代表 from (ecc编号)
void dfs(int u, int f) {
    from[u] = f;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (from[to] || bridge[e]) continue;  // to已访问，或者该边是桥
        dfs(to, f);
    }
}

vector<int> adj[maxn];
void rebuild() {
    for (int u = 1; u <= n; u++) {
        for (int e = head[u]; ~e; e = edges[e].nxt) {
            int v = edges[e].to;
            int fu = from[u], fv = from[v];
            if (fu == fv) continue;
            adj[fu].push_back(fv);
        }
    }
}

int sz[maxn], son[maxn], top[maxn], tr_id[maxn];
int par[maxn][20], dep[maxn];
void dfs2(int u, int p) {
    sz[u] = 1;
    dep[u] = dep[p] + 1;
    par[u][0] = p;
    for (int j = 1; j <= 19; j++) par[u][j] = par[par[u][j-1]][j-1];
    int maxsz = -1;
    for (int i = 0; i < adj[u].size(); i++) {
        int to = adj[u][i];
        if (to == p) continue;
        dfs2(to, u);
        sz[u] += sz[to];
        if (sz[to] > maxsz) maxsz = sz[to], son[u] = to;
    }
}

void dfs3(int u, int p, int topf) {
    top[u] = topf;
    tr_id[u] = ++id;
    if (son[u]) dfs3(son[u], u, topf);
    for (int i = 0; i < adj[u].size(); i++) {
        int to = adj[u][i];
        if (to == p || to == son[u]) continue;
        dfs3(to, u, to);
    }
}

struct tree_node {
    int sum;
    bool lazy;
} tr[maxn<<2];

void push_up(int cur) {
    tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum;
}

void push_down(int cur) {
    if (!tr[cur].lazy) return;
    tr[cur].lazy = 0;
    int l = cur<<1, r = cur<<1|1;
    tr[l].lazy = tr[r].lazy = 1;
    tr[l].sum = tr[r].sum = 0;
}

void update(int cur, int l, int r, int L, int R) {
    if (l >= L && r <= R) {
        tr[cur].lazy = 1;
        tr[cur].sum = 0;
        return;
    }
    push_down(cur);
    int mid = (l+r) >> 1;
    if (L <= mid) update(cur<<1, l, mid, L, R);
    if (R > mid) update(cur<<1|1, mid+1, r, L, R);
    push_up(cur);
}

int query(int cur, int l, int r, int L, int R) {
    if (l >= L && r <= R) return tr[cur].sum;
    push_down(cur);
    int mid = (l+r) >> 1;
    int res = 0;
    if (L <= mid) res += query(cur<<1, l, mid, L, R);
    if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
    return res;
}

void build_tree(int cur, int l, int r) {
    if (l == r) {
        tr[cur].sum = 1;
        return;
    }
    int mid = (l+r) >> 1;
    build_tree(cur<<1, l, mid);
    build_tree(cur<<1|1, mid+1, r);
    push_up(cur);
}

int jump(int u, int d) {
    int j = 0;
    while (d) {
        if (d&1) u = par[u][j];
        j++, d >>= 1;
    }
    return u;
}

int LCA(int u, int v) {
    if (dep[u] < dep[v]) swap(u,v);
    int d = dep[u] - dep[v];
    u = jump(u, d);
    if (u == v) return u;
    for (int j = 19; j >= 0; j--) {
        if (par[u][j] != par[v][j]) 
            u = par[u][j], v = par[v][j];
    }
    return par[u][0];
}


int curans;

void update_path_helper(int u, int v) {
    if (v == -1) return;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        curans -= query(1, 2, ecc, tr_id[top[u]], tr_id[u]);
        update(1, 2, ecc, tr_id[top[u]], tr_id[u]);
        u = par[top[u]][0];
    }
    if (dep[u] > dep[v]) swap(u,v);
    curans -= query(1, 2, ecc, tr_id[u], tr_id[v]);
    update(1, 2, ecc, tr_id[u], tr_id[v]);
}

void update_path(int u, int v) {
    int x = LCA(u,v);
    int d,ux,vx;

    d = dep[u] - dep[x];
    if (!d) ux = -1;
    else ux = jump(u, d-1);

    d = dep[v] - dep[x];
    if (!d) vx = -1;
    else vx = jump(v, d-1);

    update_path_helper(u, ux);
    update_path_helper(v, vx);
}

void clearall() {
    fill(head, head+n+1, -1);
    fill(dfn, dfn+n+1, 0);
    fill(low, low+n+1, 0);
    fill(from, from+n+1, 0);
    fill(bridge, bridge+(m<<1)+2, 0);
    fill(sz, sz+ecc+1, 0);
    fill(son, son+ecc+1, 0);
    fill(top, top+ecc+1, 0);
    fill(tr_id, tr_id+ecc+1, 0);
    for (int i = 1; i <= 4*ecc+5; i++) tr[i].lazy = 0;
    for (int i = 1; i <= ecc; i++) 
        for (int j = 0; j <= 19; j++) par[i][j] = 0;
    fill(dep, dep+ecc+1, 0);
    for (int i = 1; i <= n; i++) adj[i].clear();
    ecnt = id = ecc = 0;
}

int main() {
    fastio;
    int T = 0;
    fill(head, head+maxn, -1);
    while (cin >> n >> m && n && m) {
        T++;
        for (int i = 1; i <= m; i++) {
            int u,v; cin >> u >> v;
            addEdge(u,v); addEdge(v,u);
        }
        tarjan(1, 0);
        for (int i = 1; i <= n; i++) {
            if (!from[i]) dfs(i, ++ecc);
        }
        rebuild();

        id = 0;
        dfs2(1, 0);
        dfs3(1, 0, 1);
        curans = ecc-1;

        cout << "Case " << T << ":\n";
        int Q; cin >> Q;
        if (ecc == 1) {
            while (Q--) {
                int u,v; cin >> u >> v;
                cout << 0 << "\n";
            }
        } else {
            build_tree(1, 2, ecc);
            while (Q--) {
                int u,v; cin >> u >> v;
                update_path(from[u],from[v]);
                cout << curans << "\n";
            }
            cout << "\n";
        }

        clearall();
    }
}

例4 Universal Cup 9 B. Kawa Exam

题意

给定一个无向图，有 $n$ 个点和 $m$ 条边。每个点有一个颜色 $a_i$。

现在对于每条边，回答以下问题：

如果断开这条边后，统计所有的连通分量，对于每个连通分量，如果这个连通分量中出现次数最多的颜色的出现次数为 $x$，将答案加上 $x$。

对于每条边，都回答这个 ans。

其中，$1 \leq n,m,a_i \leq 10^5$。

题解

首先无向图中，考虑断开一条边对连通分量的影响。

如果断开边对联通分量有影响，说明这条边是一个桥。否则的话答案不变。

于是我们先求出边双，然后缩点，就可以得到一棵森林。

对于每一个联通分量，缩点后都是一棵树，那么有影响的边一定是某棵树上的一条边（这些边都一定是桥）。

ok，现在缩点完毕以后，问题变成断开一棵树上的边，得到两个新的连通分量，对答案有什么影响？

注意到，得到的两个连通分量是一棵子树，和子树外面的部分，我们可以用树上启发式合并，求出每棵子树对应的信息（指子树中，出现次数最多的颜色的出现次数）。

那么子树外面的部分的信息怎么办？注意到我们可以先把整棵树的信息加上，然后减去子树的贡献，这其实也能用树上启发式合并，只不过符号从 $+$ 变成 $-$ 罢了。

• 在启发式合并中，我们会遇到如下的问题：

给定一棵子树，我们要将这个子树对颜色数量的贡献减掉，每减掉一个节点，$O(1)$ 计算当前出现次数最多的颜色的出现次数。

首先，加上的话很好写，拿全局数组 cnt[] 维护，每次加一个节点的时候更新 mxcnt = max(mxcnt, cnt[a[x]]); 即可。

如果是减去呢？我们可以利用 cnt[] 数组的 count 数组！

举个例子，一棵子树里有颜色 $1,1,1,2,2$，那么我们开一个 cnt[] 数组，就有 cnt = [3,2]（cnt[1] = 3 代表颜色 $1$ 有3个）。

那么我们对 cnt[] 数组再求一次 count数组，叫 oc[]，就有 oc = [0, 1, 1]（cnt[2] = 1 代表数字 $2$ 出现了一次，cnt[3] = 1 代表数字 $3$ 出现了一次）。

我们记录此时 mxcnt = 3（出现次数最多的颜色是 $1$，出现了3次），那么其实 mxcnt 也就等于最大的 $i$，使得 oc[i] > 0。

现在，假设我们删掉了一个颜色 $1$，得到 $1,1,2,2$，那么此时 cnt = [2,2]，就有 oc = [0,2,0]，那么此时 mxcnt = 2。

所以，我们只要维护 oc 这个数组即可 $O(1)$ 得到 mxcnt。

最后注意，本题可能有自环和重边，但 tarjan 的逻辑不会被这些所影响，所以不用特殊处理。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+55;
const int maxm = 1e5+55;

int T, a[maxn];
int n, m;
int head[maxn], ecnt = 0, dfn[maxn], low[maxn], id = 0, from[maxn], ecc = 0;
bool bridge[maxm<<1];
struct Edge {
    int to, nxt, idx;
} edges[maxm<<1];
void addEdge(int u, int v, int idx) {
    Edge e = {v, head[u], idx};
    edges[ecnt] = e;
    head[u] = ecnt++;
}
void tarjan(int u, int p) {
    dfn[u] = low[u] = ++id;
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (to == p) continue;
        if (dfn[to]) low[u] = min(low[u], dfn[to]);
        else {
            tarjan(to, u);
            low[u] = min(low[u], low[to]);
            if (low[to] > dfn[u]) {
                bridge[e] = bridge[e^1] = 1;
            }
        }
    }
}
// f 代表 from (ecc编号)
vector<int> vec[maxn];
void dfs(int u, int f) {
    from[u] = f;
    vec[f].push_back(u);
    for (int e = head[u]; ~e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (from[to] || bridge[e]) continue;  // to已访问，或者该边是桥
        dfs(to, f);
    }

}

vector<pii> adj[maxn];
void rebuild() {
    for (int u = 1; u <= n; u++) {
        for (int e = head[u]; ~e; e = edges[e].nxt) {
            int v = edges[e].to;
            int fu = from[u], fv = from[v];
            if (fu == fv) continue;
            adj[fu].push_back({fv, edges[e].idx});
        }
    }
}

int ans = 0;
int mxcnt = 0;
int cnt[maxn];
bool vis[maxn];
void dfs1(int u, int p, int f) {
    vis[u] = 1;
    for (int x : vec[u]) {
        cnt[a[x]] += f;
        mxcnt = max(mxcnt, cnt[a[x]]);
    }

    for (auto [v,_] : adj[u]) {
        if (v == p) continue;
        dfs1(v, u, f);
    }
}


int sz[maxn], son[maxn], pidx[maxn];
void dfs2(int u, int p) {
    vis[u] = 1;
    sz[u] = 1;
    int maxsz = -1;
    for (auto [to, eidx] : adj[u]) {
        if (to == p) continue;
        pidx[to] = eidx;
        dfs2(to, u);
        sz[u] += sz[to];
        if (sz[to] > maxsz) {
            maxsz = sz[to];
            son[u] = to;
        }
    }
}


int oc[maxn];  // 辅助数组，代表 cnt[] 数组的 count数组
void update(int u, int f) {  // 单点更新
    for (int x : vec[u]) {
        oc[cnt[a[x]]]--;
        cnt[a[x]] += f;
        oc[cnt[a[x]]]++;
        if (f == 1) {
            mxcnt = max(mxcnt, cnt[a[x]]);
        } else {  // f == -1
            if (oc[mxcnt] == 0) {
                mxcnt = cnt[a[x]];
            }
        }
    }
}


void add(int u, int p, int f) {  // f = 1: add, f = -1: del
    update(u, f);
    for (auto [to, eidx] : adj[u]) {
        if (to == p) continue;
        add(to, u, f);
    }
}


int final_ans[maxn], sub_tree_ans[maxn], cur;
void dfs3(int u, int p, bool keep, int f) {
    vis[u] = 1;
    for (auto [to, _] : adj[u]) {
        if (to == p || to == son[u]) continue;
        dfs3(to, u, 0, f);
    }
    if (son[u]) dfs3(son[u], u, 1, f);
    for (auto [to, _] : adj[u]) {
        if (to == p || to == son[u]) continue;
        add(to, u, f);
    }
    update(u, f);
    int eidx = pidx[u];
    if (f == 1) {
        final_ans[eidx] += mxcnt;
    } else {  // f == -1
        final_ans[eidx] += mxcnt;
        final_ans[eidx] -= cur;
    }
    if (!keep) add(u, p, -f);
}



int main() {
    fastio;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        fill(head, head+n+5, -1);
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
        }
        for (int i = 1; i <= m; i++) {
            int u, v; cin >> u >> v;
            addEdge(u, v, i);
            addEdge(v, u, i);
        }

        for (int i = 1; i <= n; i++) {
            if (!dfn[i]) tarjan(i, 0);
        }
        for (int i = 1; i <= n; i++) {
            if (!from[i]) 
                dfs(i, ++ecc);
        }

        rebuild();

        for (int i = 1; i <= ecc; i++) {
            mxcnt = 0;
            if (!vis[i]) {
                dfs1(i, 0, 1);
                dfs1(i, 0, -1);
                sub_tree_ans[i] = mxcnt;
                ans += mxcnt;
            }
        }
        fill(vis, vis+n+5, 0);

        for (int i = 1; i <= ecc; i++) {
            if (!vis[i]) {
                dfs2(i, 0);
            }
        }

        fill(vis, vis+n+5, 0);
        for (int i = 1; i <= ecc; i++) {
            mxcnt = 0;
            if (!vis[i]) {
                cur = sub_tree_ans[i];
                dfs3(i, 0, 0, 1);
                add(i, 0, 1);
                dfs3(i, 0, 0, -1);
                add(i, 0, -1);
            }
        }

        for (int i = 1; i <= m; i++) {
            cout << final_ans[i] + ans;
            cout << (i==m ? "\n" : " ");
        }

        fill(vis, vis+n+5, 0);
        fill(dfn, dfn+n+5, 0);
        fill(low, low+n+5, 0);
        fill(final_ans, final_ans+m+5, 0);
        fill(sub_tree_ans, sub_tree_ans+n+5, 0);
        fill(sz, sz+n+5, 0);
        fill(son, son+n+5, 0);
        fill(pidx, pidx+n+5, 0);
        fill(oc, oc+n+5, 0);
        fill(cnt, cnt+n+5, 0);
        fill(from, from+n+5, 0);
        ecnt = 0;
        ecc = 0;
        id = 0;
        ans = 0;
        mxcnt = 0;
        cur = 0;
        fill(bridge, bridge+2*m+5, 0);
        for (int i = 1; i <= n; i++) adj[i].clear(), vec[i].clear();
    }
}

割点桥点/边双连通分量（BCC）

Contents

定义

割点

桥

点双连通

边双连通

点双连通分量

点双缩点

边双连通分量

边双缩点

算法

割点

桥

点双连通分量（dcc）

边双连通分量（ecc）

例题

例1 洛谷P3225 [HNOI2012]矿场搭建

例2 洛谷P5058 [ZJOI2004]嗅探器

例3 POJ3694 Network

例4 Universal Cup 9 B. Kawa Exam

参考链接