树的直径
Contents
定义
树的直径是指:在一棵有权/无权树中,所有简单路径中,权值和最大的那一条。
树的直径有以下性质:(以下,我们假设所有边上的权值均 $\geq 0$)。
-
直径一定是由两个 leaf 组成
-
对于任意一个节点 $u$,距离它最远的一个节点,必然为直径的其中一端。
-
在一棵树上,任取两个点集 $S_1, S_2$,设 $S_1$ 这个点集的直径是 $(u_1,v_1)$,设 $S_2$ 这个点集的直径是 $(u_2, v_2)$,那么令 $S = S_1 \cup S_2$。则点集 $S$ 的直径只可能为以下 $6$ 种的之一:
$$(u_1, v_1), (u_2, v_2), (u_1, u_2), (u_1, v_2), (v_1, u_2), (v_2, u_2)$$
即,新的直径一定由原先 $4$ 个端点组成。
证明:第二个性质
我们设直径是 $(s,t)$,并且设节点 $a$ 距离最远的节点是 $b$,其中 $b \neq s, b \neq t$。
Case1:$a$ 位于直径 $(s,t)$ 上:
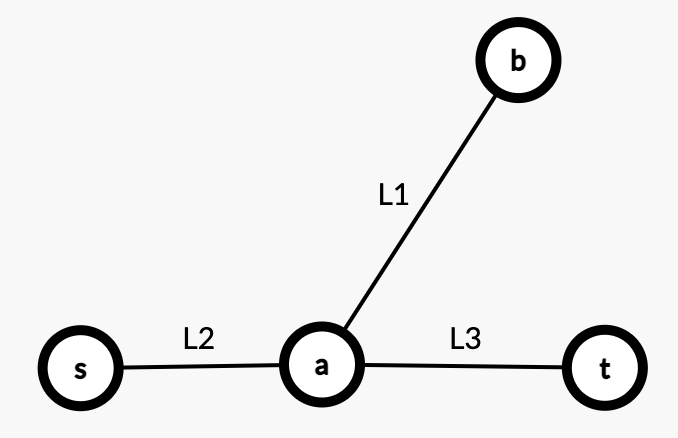
如上,有 $L_1 > L_2$,$L_1 > L_3$。且 $L_2 + L_3$ 为直径。
那么 $L_1 + L_3 > L_2 + L_3$,$L_1 + L_2 > L_2 + L_3$。
所以 $L_1 + L_3$ 或者 $L_1 + L_2$ 才是直径。contradiction。
Case2:$(a,b)$ 之间的路径横穿了 $(s,t)$,交点为 $x$。
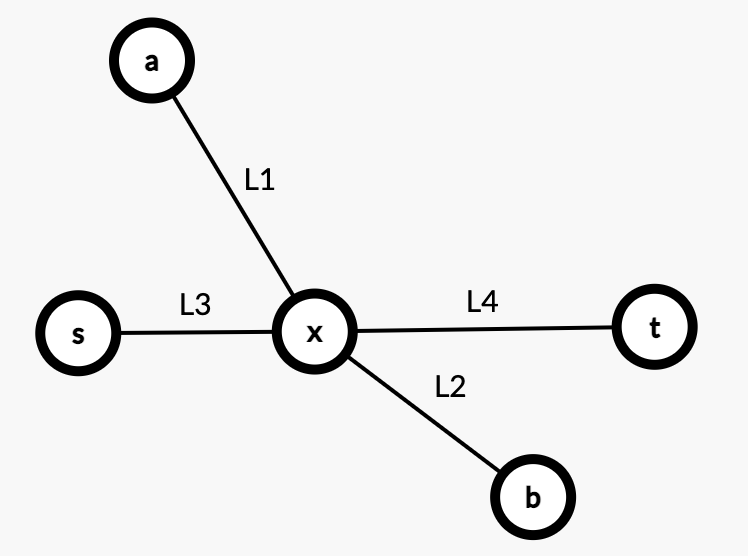
如上,因为距离 $a$ 最远的是 $b$,所以有 $L_1 + L_2 > L_1 + L_3$,$L_1 + L_2 > L_1 + L_3$。
那么 $L_2 > L_3$,$L_2 > L_4$。
所以 $L_2 + L_3 > L_3 + L_4$,$L_2 + L_4 > L_3 + L_4$。
所以 $L_2 + L_3$ 或者 $L_2 + L_4$ 才是直径。contradiction。
Case3:$(a,b)$ 之间的路径没有穿过 $(s,t)$,但是 $(a,b)$ 路径上,有一个距离 $(s,t)$ 最短的点 $x$,并且这个 $x$ 通过 $y$ 与 $(s,t)$ 相交。
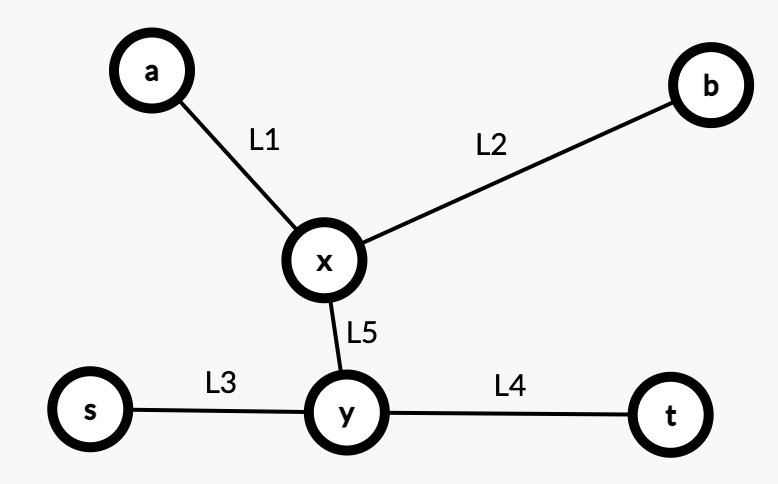
如上,因为距离 $a$ 最远的是 $b$,所以有 $L_1 + L_2 > L_1 + L_5 + L_4$,$L_1 + L_2 > L_1 + L_5 + L_3$。
所以有 $L_2 > L_5 + L_4$,$L_2 > L_5 + L_3$。
所以 $L_3 + L_5 + L_2 > L_3 + L_4$,$L_4 + L_5 + L_2 > L_3 + L_4$。
所以 $L_3 + L_5 + L_2$ 或者 $L_4 + L_5 + L_2$ 才是直径。contradiction。
• 第三个性质的证明不会,先咕着
求树的直径
求树的直径有两种方法:两次DFS 和 DP。
法一:两次DFS(推荐)
由性质 $2$,我们可以以任意节点为根,进行DFS。得到一个距离最远的点 $u$ (这个节点的深度最深)。
然后再以 $u$ 为根,进行第二次DFS。得到距离最远的点 $v$。那么 $(u,v)$ 就是直径了。
两次DFS:代码
int n, dep[maxn], d1, d2; // d1: 直径一端,d2: 直径另外一端
void dfs1(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dep[to] = dep[u] + 1;
dfs1(to, u);
}
}
int main() {
dep[1] = 0; dfs1(1, 0); // 第一次 DFS (以 1 为根)
d1 = 1;
for (int u = 1; u <= n; u++) {
if (dep[u] > dep[d1]) {
d1 = u;
}
}
dep[d1] = 0; dfs1(d1, 0); // 第二次 DFS (以直径端点 d1 为根)
d2 = d1;
for (int u = 1; u <= n; u++) {
if (dep[u] > dep[d2]) {
d2 = u;
}
}
}
法二:树形DP
固定 $1$ 为根。记录每个节点向下,最远能延伸的两个节点的距离 $d_1,d_2$,那么直径就是所有 $d_1+d_2$ 的最大值。
树形DP:代码
int d1[maxn], d2[maxn], d; // d 是直径的值
void dfs(int u, int p) {
d1[u] = d2[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
int t = d1[v] + 1;
if (t > d1[u])
d2[u] = d1[u], d1[u] = t;
else if (t > d2[u])
d2[u] = t;
}
d = max(d, d1[u] + d2[u]);
}
int main() {
dfs(1, 0);
}
例题
例1 CF911F Tree Destruction
题意
给定一棵 $n$ 个节点的无权树,然后进行 $(n-1)$ 次以下操作,每次操作分以下三步:
- 选择两个leaf
- 将这两个leaf之间的距离,加到
ans中。 - 将这两个leaf其中之一,删掉。
初始状态下,ans = 0。求 ans 的最大值,并且输出方案。
其中,$2 \leq n \leq 2 \times 10^5$
题解
利用树的直径的第二个性质:任意一个节点 $u$,距离最远的一定是直径的一端。
所以我们要最大化最终答案,我们可以最大化每个节点的贡献。所以我们只要保留直径,先将剩下的叶子删掉就行了。
思路如下:
- 找到直径 $(u,v)$
- 使用类似于拓扑排序的方法,维护所有
deg = 1的节点(除了直径两端的两个节点 $u,v$),将它们删去。这个过程,本质上是将直径看作树干,然后逐一拔掉所有的树枝。 - 最后只剩下一条直径了,从任意一端开始删除即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1, n, dep[maxn], d1, d2; // d1: 直径一端,d2: 直径另外一端
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void dfs1(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dep[to] = dep[u] + 1;
dfs1(to, u);
}
}
ll ans = 0;
struct node {
int u,v,r;
} path[maxn];
int tail = 0;
int deg[maxn];
vector<int> leaf;
int dis1[maxn], dis2[maxn];
// 初始化:找出每个节点到 d1, d2的距离
void init() {
dep[d1] = 0; dfs1(d1, 0);
memcpy(dis1, dep, sizeof(dep));
dep[d2] = 0; dfs1(d2, 0);
memcpy(dis2, dep, sizeof(dep));
}
// 第一步:拔掉所有除了 d1, d2 以外的叶子
void solve1() {
for (int i = 1; i <= n; i++) {
if (deg[i] == 1 && i != d1 && i != d2) leaf.push_back(i);
}
while (leaf.size()) {
int u = leaf.back(); leaf.pop_back();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
deg[to]--;
if (deg[to] == 1) {
leaf.push_back(to);
}
}
int t;
if (dis1[u] > dis2[u]) t = d1, ans += (ll)dis1[u];
else t = d2, ans += (ll)dis2[u];
path[++tail] = {u,t,u};
}
}
// 第二步:拔掉直径
void solve2() {
leaf.push_back(d2);
while (leaf.size()) {
int u = leaf.back(); leaf.pop_back();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
deg[to]--;
if (deg[to] == 1) {
leaf.push_back(to);
}
}
ans += (ll)(dis1[u]);
path[++tail] = {u, d1, u};
}
}
int main() {
cin >> n;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
deg[u]++, deg[v]++;
}
dep[1] = 0; dfs1(1, 0);
d1 = 1;
for (int u = 1; u <= n; u++) {
if (dep[u] > dep[d1]) {
d1 = u;
}
}
dep[d1] = 0; dfs1(d1, 0);
d2 = d1;
for (int u = 1; u <= n; u++) {
if (dep[u] > dep[d2]) {
d2 = u;
}
}
init();
solve1();
solve2();
cout << ans << endl;
for (int i = 1; i <= n-1; i++) {
cout << path[i].u << " " << path[i].v << " " << path[i].r << "\n";
}
}
例2 CF1192B Dynamic Diameter
题意
给定 $n$ 个节点的有权树,和 $q$ 次询问。
每次询问格式为 $d ~ e$:将第 $d$ 条边的权值改为 $e$。
在每次询问之后,回答:此时树中直径的长度。
其中,$2 \leq n \leq 10^5, 1 \leq q \leq 10^5$。
欧拉序介绍
欧拉序和DFS序不同的地方在于:
在一个节点 $u$ 访问完它的一个child $v$ 之后,回溯到 $u$ 时,也会将 $u$ 记录进序列中。
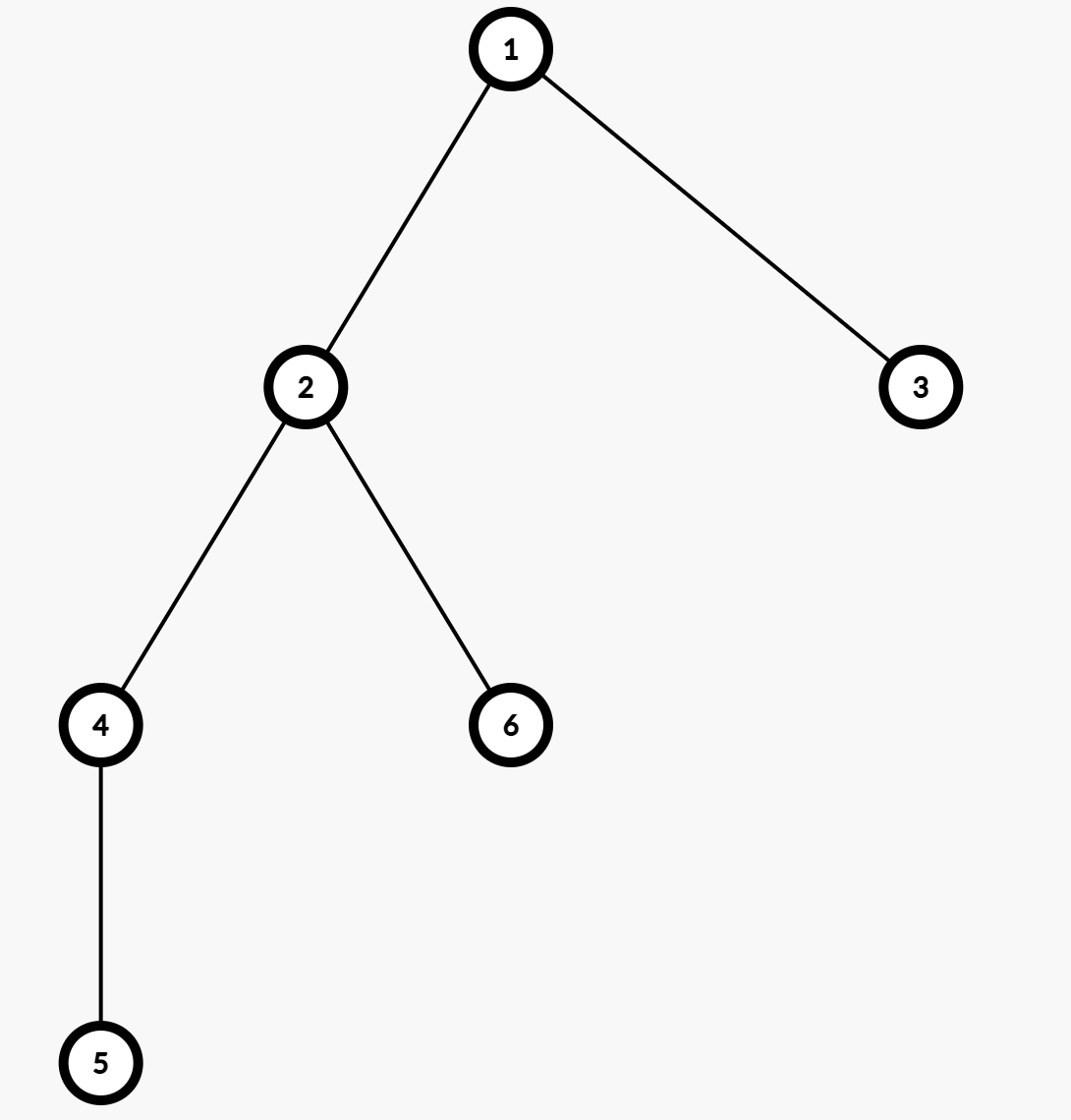
如上图,访问的顺序如果是 $1 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 6 \rightarrow 3$ 的话,得到的欧拉序就是:
$[1,2,4,5,4,2,6,2,1,3,1]$。
欧拉序有以下性质:
- 对于 $n$ 个节点的树,欧拉序的长度一定为 $2n-1$。
- 在欧拉序中任取两个index $i,j$,它分别对应的节点是 $u,v$ 的话。在 $[i,j]$ 这段欧拉序中,
depth最小的index 所对应的节点 $x$ 就是 $LCA(u,v)$。
• 例如,我们把上述欧拉序按照 depth 重新写一下,就会得到:[0,1,2,3,2,1,2,1,0,1,0]。
我们任取其中一段,比如:[0,1,2,3,2,1,2,1,0,1,0],那么对应的就是 $5,4,2,6$ 这几个节点。可以发现这一段中,depth 最小值为 $1$,对应的节点是 $2$。而这一段的两端,对应的就是节点 $5,6$。这说明 节点 $5,6$ 的 LCA 就是 节点 $2$。
证明性质 $1$:易知,每条 edge 会在欧拉序中贡献 $2$ 个位置。而根节点 $1$ 又会额外贡献一个。所以总共是 $2 \times (n-1) + 1 = 2n-1$。
证明性质 $2$:设一段欧拉序的两端,对应的节点分别为 $u,v$。令 $x = LCA(u,v)$。那么这一段欧拉序,一定会经过 $x$,且一定是完全在 $x$ 所在的子树内的,不可能出现在子树外的节点。所以 $x$ 一定是这一段 depth 最小的那个节点。
法一 欧拉序 题解
有两种方法,一种是 欧拉序,复杂度 $O(n\log n)$。还有一种是 DFS序,时间复杂度 $O(n\log^2 n)$。
这里介绍一下 法一欧拉序。
我们固定 $1$ 为根。求出每个节点的 depth。然后求出欧拉序。
有了欧拉序以后,我们可以用线段树维护这个欧拉序序列。我们设这个序列为 $a[]$。
然后询问两个节点 $u,v$ 之间的距离,就可以先找到 $u$ 对应在欧拉序中的位置 $l$(可能对应多个位置,任选一个即可),$v$ 对应在欧拉序中的位置 $r$。由树上差分,可知 $u,v$ 的距离等于 $d_u + d_v - 2 \times d_x$,则有:
$$dist(u,v) = a[l] + a[r] - 2 \times \min\limits_{l \leq k \leq r}a[k]$$
所以整个问题可以转化为一个序列上的问题:给定一个数组 $a[]$,求:
$$a[l] + a[r] - 2 \times \min\limits_{l \leq k \leq r}a[k]$$
的最大值?(其中 $l,r$ 任选)
这个式子有 $2$ 个变量,$l,r$,我们需要用线段树来维护一些额外信息,来将其转化为一个变量的问题。
设
$$D[L,R] = \max\limits_{l \leq r, l,r \in [L,R]} \{a[l] + a[r] - 2 \times \min\limits_{l \leq k \leq r}a[k]\}$$
我们考虑固定其中一个变量(比如 $l$),那么剩下的变量就只有 $r$ 了,我们就可以考虑 $a[r] - 2 \times \min\limits_{l \leq k \leq r}a[k]$。
设
$$rmax[L,R] = \max\limits_{l \leq r, l,r \in [L,R]} \{a[r] - 2 \times \min\limits_{l \leq k \leq r}a[k] \}$$
$$lmax[L,R] = \max\limits_{l \leq r, l,r \in [L,R]} \{a[l] - 2 \times \min\limits_{l \leq k \leq r}a[k] \}$$
则,我们有以下转移方程:
$$rmax[L,R] = \max \begin{cases}
rmax[L, mid] \\
rmax[mid+1, R] \\
max[mid+1,R] - 2\times min[L, mid]
\end{cases}
$$
$$lmax[L,R] = \max \begin{cases}
lmax[L, mid] \\
lmax[mid+1, R] \\
max[L, mid] - 2\times min[mid+1, R]
\end{cases}
$$
$$D[L,R] = \max \begin{cases}
D[L, mid] \\
D[mid+1, R] \\
max[L, mid] + rmax[mid+1, R] \\
lmax[L, mid] + max[mid+1, R]
\end{cases}
$$
最后,答案就是 $D[1,2n-1]$。
上述转移方程有几个点需要注意:
Q1. 为什么 $D[L,R]$ 可以由 $max[L, mid] + rmax[mid+1, R]$ 转移而来?$rmax[mid+1, R]$ 并没有考虑到 $[L,mid]$ 这一段中的最小值啊?
A1. 如果最终答案需要考虑到 $[L,mid]$ 这一段的最小值,那么说明 $D[L,R]$ 应该由 $lmax[L, mid] + max[mid+1, R]$ 或者 $D[L, mid]$ 转移而来。这也说明了为什么我们需要使用 $lmax, rmax$ 进行两次转移。
• 另外,$rmax[L,R]$ 和 $lmax[L,R]$ 的转移过程同理。
最后一个问题:修改边的权值,怎么处理?
因为我们所有的距离都是基于 depth 的,所以,把修改边的权值改为修改 depth 即可。
假设有一个边 $(u,v)$,令 $v$ 为 child。设原来的权值为 $e_1$,现在改为 $e_2$,那么就相当于给 $v$ 的 subtree 中的所有节点的 depth 加上 $(e_2 - e_1)$。
法二 DFS序 题解
根据树的直径的性质 $3$,我们可以求出整棵树的欧拉序,然后用线段树维护点集的直径。比如 $[5,8]$ 这个区间,维护的就是欧拉序为 $[5,6,7,8]$ 的点集的直径。
可得,$[1,n]$ 这个点集的直径就是整棵树的直径。
然后在合并区间 $[L, mid]$ 和 $[mid+1, R]$ 时,就可以枚举 $6$ 种情况的直径长度,得到 $[L,R]$ 对应点集的直径。
有几个问题:
Q1. 怎么得到每种情况的直径长度?
A1. 和上一个方法一样,固定 $1$ 为根,然后两个节点 $(u,v)$ 之间的距离就可以利用 $d_u + d_v - 2 \times d_{LCA(u,v)}$ 来求出。
Q2. 修改权值时,直径会受到影响吗?
A2. 会的。但是如果我们修改了权值,影响了一个 subtree(在DFS序上就是一段连续区间),则如果一个点集完全存在于这个 subtree 之内,就不会受到影响。我们只需要考虑 点集 与 subtree 拥有相交区间,且点集没有被完全覆盖的情况。这实际上就是线段树 update 过程中正常的 lazy tag 和 push_up() 操作。所以不需要特殊处理,该怎么写怎么写就行。
注:本题没有用法二来写,因为本题不需要求出直径具体的节点,只要长度。下一题会使用到法二,代码可以参见下一个例题。
法一 欧拉序 代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 1e6;
struct Edge {
int from, to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 2, n, q;
ll W;
void addEdge(int u, int v, ll w) {
Edge e = {u, v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dep[maxn<<1]; // 欧拉序的 dep
int in[maxn], out[maxn]; // in[u]: 节点 u 在欧拉序中的起点
int ori_dep[maxn]; // 原本在树中的depth(不算weight)
int id = 0;
void dfs(int u, int p, ll d) {
dep[++id] = d;
in[u] = out[u] = id;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
ll w = edges[e].w;
ori_dep[to] = ori_dep[u] + 1;
dfs(to, u, d + w);
dep[++id] = d;
out[u] = id;
}
}
int m;
struct tree_node {
ll mini, maxi, lmax, rmax, ans;
ll lazy = 0;
} tr[maxn<<3];
void push_up(int cur) {
int l = cur<<1, r = l+1;
tr[cur].mini = min(tr[l].mini, tr[r].mini);
tr[cur].maxi = max(tr[l].maxi, tr[r].maxi);
tr[cur].lmax = max(max(tr[l].lmax, tr[r].lmax), tr[l].maxi - 2LL * tr[r].mini);
tr[cur].rmax = max(max(tr[l].rmax, tr[r].rmax), tr[r].maxi - 2LL * tr[l].mini);
tr[cur].ans = max(max(tr[l].ans, tr[r].ans), max(tr[l].maxi + tr[r].rmax, tr[r].maxi + tr[l].lmax));
}
void push_down(int cur) {
if (!tr[cur].lazy) return;
ll lazy = tr[cur].lazy;
int l = cur<<1, r = l|1;
tr[cur].lazy = 0;
tr[l].lazy += lazy; tr[r].lazy += lazy;
tr[l].maxi += lazy; tr[r].maxi += lazy;
tr[l].mini += lazy; tr[r].mini += lazy;
tr[l].lmax -= lazy; tr[r].lmax -= lazy;
tr[l].rmax -= lazy; tr[r].rmax -= lazy;
}
void build(int cur, int l, int r) {
if (l == r) {
tr[cur].mini = tr[cur].maxi = dep[l];
tr[cur].lmax = tr[cur].rmax = -dep[l];
tr[cur].ans = 0;
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
void update(int cur, int l, int r, int L, int R, ll x) {
if (l >= L && r <= R) {
tr[cur].lazy += x;
tr[cur].maxi += x;
tr[cur].mini += x;
tr[cur].lmax -= x;
tr[cur].rmax -= x;
return;
}
push_down(cur);
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, x);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
push_up(cur);
}
ll query(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) {
return tr[cur].ans;
}
push_down(cur);
int mid = (l+r) >> 1;
ll res = 0;
if (L <= mid) res += query(cur<<1, l, mid, L, R);
if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
push_up(cur);
return res;
}
ll last = 0;
int main() {
cin >> n >> q >> W;
for (int i = 1; i < n; i++) {
int u,v; ll w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
dfs(1, 0, 0);
m = 2*n - 1;
build(1, 1, m);
while (q--) {
ll d,e; cin >> d >> e;
d = (d + last) % (n-1) + 1;
d <<= 1; // 编号从 2 开始
e = (e + last) % W;
ll x = e - edges[d].w;
edges[d].w = edges[d^1].w = e;
int u = edges[d].from, v = edges[d].to;
if (ori_dep[u] > ori_dep[v]) swap(u,v);
update(1, 1, m, in[v], out[v], x);
last = query(1, 1, m, 1, m);
cout << last << "\n";
// 将第 d 条边的 weight 改为 e
}
}
例3 Lightning Routing I
题意
给定 $n$ 个节点的有权树,和 $q$ 次询问。
每次询问有 $2$ 种:
$C ~ e_i ~ w_i$:将第 $e_i$ 条边的权值改为 $w_i$
$Q ~ v_i$:询问距离 $v_i$ 最远的节点的距离。
其中,$1 \leq n \leq 10^5, 1 \leq q \leq 10^5$。
题解
和上一题完全一样。
需要注意的是 $Q ~ v_i$ 这个询问。由树直径的基本性质,对于任意一个节点 $v$,距离最远的节点一定是直径的其中一端。那么问题可以转化为:
先求出直径的两端,然后判断一下哪一端距离 $v$ 最远。
• 这样的话,法一欧拉序就需要在线段树区间合并的时候,加一些额外的信息来 track 具体是哪些index被用到了转移中。
法一(欧拉序)代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 1e6;
struct Edge {
int from, to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 2, n, q;
ll W;
void addEdge(int u, int v, ll w) {
Edge e = {u, v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dep[maxn<<1]; // 欧拉序的 dep
int in[maxn], out[maxn]; // in[u]: 节点 u 在欧拉序中的起点
int ori_dep[maxn]; // 原本在树中的depth(不算weight)
int id = 0;
void dfs(int u, int p, ll d) {
dep[++id] = d;
in[u] = out[u] = id;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
ll w = edges[e].w;
ori_dep[to] = ori_dep[u] + 1;
dfs(to, u, d + w);
dep[++id] = d;
out[u] = id;
}
}
int m;
struct tree_node {
ll mini, maxi, lmax, rmax, ans;
ll lazy = 0;
int mini_idx, maxi_idx, lmax_idx, rmax_idx, L, R;
} tr[maxn<<3];
void push_up(int cur) {
int l = cur<<1, r = l+1;
if (tr[l].mini < tr[r].mini) {
tr[cur].mini = tr[l].mini;
tr[cur].mini_idx = tr[l].mini_idx;
} else {
tr[cur].mini = tr[r].mini;
tr[cur].mini_idx = tr[r].mini_idx;
}
if (tr[l].maxi > tr[r].maxi) {
tr[cur].maxi = tr[l].maxi;
tr[cur].maxi_idx = tr[l].maxi_idx;
} else {
tr[cur].maxi = tr[r].maxi;
tr[cur].maxi_idx = tr[r].maxi_idx;
}
if (tr[l].lmax > tr[r].lmax) {
tr[cur].lmax = tr[l].lmax;
tr[cur].lmax_idx = tr[l].lmax_idx;
} else {
tr[cur].lmax = tr[r].lmax;
tr[cur].lmax_idx = tr[r].lmax_idx;
}
if (tr[l].maxi - 2LL * tr[r].mini > tr[cur].lmax) {
tr[cur].lmax = tr[l].maxi - 2LL * tr[r].mini;
tr[cur].lmax_idx = tr[l].maxi_idx;
}
if (tr[l].rmax > tr[r].rmax) {
tr[cur].rmax = tr[l].rmax;
tr[cur].rmax_idx = tr[l].rmax_idx;
} else {
tr[cur].rmax = tr[r].rmax;
tr[cur].rmax_idx = tr[r].rmax_idx;
}
if (tr[r].maxi - 2LL * tr[l].mini > tr[cur].rmax) {
tr[cur].rmax = tr[r].maxi - 2LL * tr[l].mini;
tr[cur].rmax_idx = tr[r].maxi_idx;
}
if (tr[l].ans > tr[r].ans) {
tr[cur].L = tr[l].L;
tr[cur].R = tr[l].R;
tr[cur].ans = tr[l].ans;
} else {
tr[cur].L = tr[r].L;
tr[cur].R = tr[r].R;
tr[cur].ans = tr[r].ans;
}
if (tr[l].maxi + tr[r].rmax > tr[cur].ans) {
tr[cur].ans = tr[l].maxi + tr[r].rmax;
tr[cur].L = tr[l].maxi_idx;
tr[cur].R = tr[r].rmax_idx;
}
if (tr[r].maxi + tr[l].lmax > tr[cur].ans) {
tr[cur].ans = tr[r].maxi + tr[l].lmax;
tr[cur].L = tr[l].lmax_idx;
tr[cur].R = tr[r].maxi_idx;
}
}
void push_down(int cur) {
if (!tr[cur].lazy) return;
ll lazy = tr[cur].lazy;
int l = cur<<1, r = l|1;
tr[cur].lazy = 0;
tr[l].lazy += lazy; tr[r].lazy += lazy;
tr[l].maxi += lazy; tr[r].maxi += lazy;
tr[l].mini += lazy; tr[r].mini += lazy;
tr[l].lmax -= lazy; tr[r].lmax -= lazy;
tr[l].rmax -= lazy; tr[r].rmax -= lazy;
}
void build(int cur, int l, int r) {
if (l == r) {
tr[cur].mini = tr[cur].maxi = dep[l];
tr[cur].lmax = tr[cur].rmax = -dep[l];
tr[cur].ans = 0;
tr[cur].mini_idx = tr[cur].maxi_idx = tr[cur].lmax_idx = tr[cur].rmax_idx = tr[cur].L = tr[cur].R = l;
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
void update(int cur, int l, int r, int L, int R, ll x) {
if (l >= L && r <= R) {
tr[cur].lazy += x;
tr[cur].maxi += x;
tr[cur].mini += x;
tr[cur].lmax -= x;
tr[cur].rmax -= x;
return;
}
push_down(cur);
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, x);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
push_up(cur);
}
ll query(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) {
return tr[cur].ans;
}
push_down(cur);
int mid = (l+r) >> 1;
ll res = 0;
if (L <= mid) res += query(cur<<1, l, mid, L, R);
if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
push_up(cur);
return res;
}
ll query_min(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) {
return tr[cur].mini;
}
push_down(cur);
int mid = (l+r) >> 1;
ll r1 = 1e18, r2 = 1e18;
if (L <= mid) r1 = query_min(cur<<1, l, mid, L, R);
if (R > mid) r2 = query_min(cur<<1|1, mid+1, r, L, R);
push_up(cur);
return min(r1, r2);
}
ll dis(int l, int r) {
if (l > r) swap(l,r);
ll al = query_min(1, 1, m, l, l), ar = query_min(1, 1, m, r, r);
ll mi = query_min(1, 1, m, l, r);
return al + ar - 2LL * mi;
}
int main() {
fastio;
cin >> n;
for (int i = 1; i < n; i++) {
int u,v; ll w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
dfs(1, 0, 0);
m = 2*n - 1;
assert(id == m);
build(1, 1, m);
cin >> q;
while (q--) {
char op;
cin >> op;
if (op == 'C') {
// 将第 d 条边的 weight 改为 e
ll d,e; cin >> d >> e;
d <<= 1; // 编号从 2 开始
ll x = e - edges[d].w;
edges[d].w = edges[d^1].w = e;
int u = edges[d].from, v = edges[d].to;
if (ori_dep[u] > ori_dep[v]) swap(u,v);
update(1, 1, m, in[v], out[v], x);
} else {
int v; cin >> v;
v = in[v];
int L = tr[1].L, R = tr[1].R;
ll dis1 = dis(L, v);
ll dis2 = dis(v, R);
cout << max(dis1, dis2) << "\n";
}
}
}
法二(DFS序)代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 1e6;
struct Edge {
int from, to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 2, n, q;
void addEdge(int u, int v, ll w) {
Edge e = {u, v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dep[maxn];
int par[maxn][19], idcnt = 0, in[maxn], out[maxn], ver[maxn]; // in[u] ..., ver[id]: the id which corresponds to u
int ori_dep[maxn]; // 原本在树中的depth(不算weight)
void dfs(int u, int p) {
in[u] = ++idcnt;
ver[idcnt] = u;
par[u][0] = p;
for (int j = 1; j <= 18; j++) par[u][j] = par[par[u][j-1]][j-1];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (to == p) continue;
ori_dep[to] = ori_dep[u] + 1;
dep[to] = dep[u] + w;
dfs(to, u);
}
out[u] = idcnt;
}
int jump(int u, int d) {
for (int j = 0; j <= 18; j++) {
if (d & (1<<j)) u = par[u][j];
}
return u;
}
int lca(int u, int v) {
if (ori_dep[u] < ori_dep[v]) swap(u,v);
u = jump(u, ori_dep[u] - ori_dep[v]);
for (int j = 18; j >= 0; j--) {
if (par[u][j] != par[v][j]) u = par[u][j], v = par[v][j];
}
if (u == v) return u;
return par[u][0];
}
struct tree_1 {
struct tree_node_1 {
ll d = 0, lazy = 0;
};
tree_node_1 tr[maxn<<2];
void build(int cur, int l, int r) {
if (l == r) {
tr[cur].d = dep[ver[l]];
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
}
void push_down(int cur) {
if (!tr[cur].lazy) return;
int l = cur<<1, r = l|1;
ll lazy = tr[cur].lazy;
tr[l].lazy += lazy, tr[r].lazy += lazy;
tr[l].d += lazy, tr[r].d += lazy;
tr[cur].lazy = 0;
}
void update(int cur, int l, int r, int L, int R, ll delta) {
if (l >= L && r <= R) {
tr[cur].lazy += delta;
tr[cur].d += delta;
return;
}
push_down(cur);
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, delta);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, delta);
}
ll query(int cur, int l, int r, int p) {
if (l == r) return tr[cur].d;
push_down(cur);
int mid = (l+r) >> 1;
if (p <= mid) return query(cur<<1, l, mid, p);
return query(cur<<1|1, mid+1, r, p);
}
ll query_dis(int id1, int id2) {
ll d1 = query(1, 1, n, id1), d2 = query(1, 1, n, id2);
ll u1 = ver[id1], u2 = ver[id2];
ll x = lca(u1, u2);
int idx = in[x];
ll dx = query(1, 1, n, idx);
return d1 + d2 - 2LL * dx;
}
} tr1;
struct tree_2 {
struct tree_node_2 {
int id1, id2; // 直径的 id
};
tree_node_2 tr[maxn<<2];
void push_up(int cur) {
int l = cur<<1, r = cur<<1|1;
int l_id1 = tr[l].id1, l_id2 = tr[l].id2, r_id1 = tr[r].id1, r_id2 = tr[r].id2;
ll len = -1;
ll dis1 = tr1.query_dis(l_id1, r_id1);
ll dis2 = tr1.query_dis(l_id1, r_id2);
ll dis3 = tr1.query_dis(l_id2, r_id1);
ll dis4 = tr1.query_dis(l_id2, r_id2);
ll dis5 = tr1.query_dis(l_id1, l_id2);
ll dis6 = tr1.query_dis(r_id1, r_id2);
if (dis1 > len) tr[cur] = {l_id1, r_id1}, len = dis1;
if (dis2 > len) tr[cur] = {l_id1, r_id2}, len = dis2;
if (dis3 > len) tr[cur] = {l_id2, r_id1}, len = dis3;
if (dis4 > len) tr[cur] = {l_id2, r_id2}, len = dis4;
if (dis5 > len) tr[cur] = {l_id1, l_id2}, len = dis5;
if (dis6 > len) tr[cur] = {r_id1, r_id2}, len = dis6;
}
void build(int cur, int l, int r) {
if (l == r) {
tr[cur].id1 = tr[cur].id2 = l;
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
void update(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) return; // 完全覆盖不用更新
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R);
if (R > mid) update(cur<<1|1, mid+1, r, L, R);
push_up(cur);
}
} tr2;
int main() {
cin >> n;
for (int i = 1; i < n; i++) {
int u,v; ll w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
dfs(1, 0);
tr1.build(1, 1, n);
tr2.build(1, 1, n);
cin >> q;
while (q--) {
char op;
cin >> op;
if (op == 'C') {
// 将第 d 条边的 weight 改为 e
ll d,e; cin >> d >> e;
d <<= 1; // 编号从 2 开始
ll x = e - edges[d].w;
edges[d].w = edges[d^1].w = e;
int u = edges[d].from, v = edges[d].to;
if (ori_dep[u] > ori_dep[v]) swap(u,v);
tr1.update(1, 1, n, in[v], out[v], x);
tr2.update(1, 1, n, in[v], out[v]);
} else {
int v; cin >> v;
v = in[v]; // v 的 id 编号
int id1 = tr2.tr[1].id1, id2 = tr2.tr[1].id2;
ll dis1 = tr1.query_dis(id1, v);
ll dis2 = tr1.query_dis(v, id2);
cout << max(dis1, dis2) << "\n";
}
}
}
