换根DP
Contents
介绍
换根DP是一种特殊的树形DP。主要特点在于需要进行两次DFS。
第一次DFS:固定任意节点(一般为 $1$)为根。对于每一个节点 $u$,仅考虑 $u$ 的subtree,求出这样的答案 $dp[u]$。
第二次DFS:令最终答案为 $ans[u]$,则可知 $ans[1] = dp[1]$。然后我们需要通过已知的 $ans[u]$,来推出它的child $ans[to]$ 的值。一般我们由 $ans[u]$ 来推导 $ans[to]$ 时,需要考虑到换根时 $to$ 子树内的贡献,和子树外的贡献 变化。
套路
我们考虑一下一种general的情况:从 $u$ 换根到 $v$。
此时我们一定位于 dfs(u) 中,并且已经求出了 $ans[u]$。现在要求 $ans[v]$。(注:这里的 $ans[u]$ 是广义的,代表 $u$ 相关的信息。不一定真的是最终的 $ans$,比如例4)
那么换根前是这样:
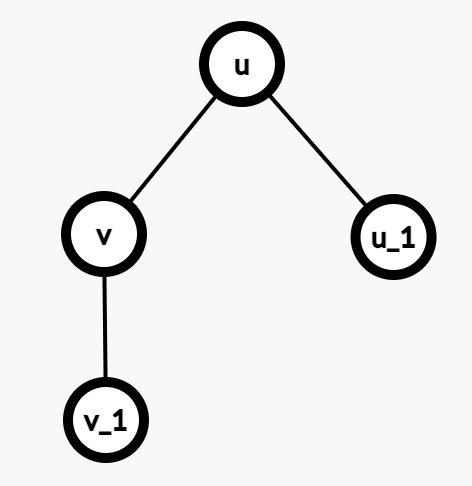
换根后,是这样:
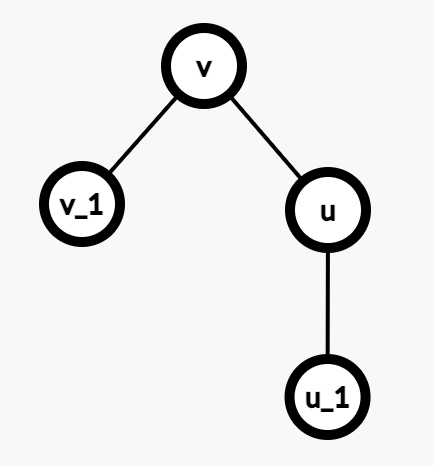
步骤如下:
- 基于 $ans[u]$,将 $u$ 的child $v$ 所带来的贡献删掉,得到 $dp2[u]$。
- 基于 $dp[v]$,将 $u$ 作为一个新的child 加给 $v$(实际上,就是将 $dp2[u]$ 的贡献加给 $dp[v]$),得到 $ans[v]$。
• 注意,这里的 $dp2[u]$ 实际上是一个临时的变量。对于每一个 $v$ 而言,$dp2[u]$ 互不相同。
例题
例1 洛谷P3478 [POI2008]STA-Station
题意
给定 $n$ 个节点的树,求一个节点 $u$ 使得 $u$ 到其他节点的距离和最大。
即,求出 $u$,使得 $\sum\limits_v d(u,v)$ 最大。
题解
首先固定 $1$ 为根,进行一次DFS。
令 dp[u] 为第一次DFS,只考虑 $u$ 的子树内的答案。(考虑深度和即可)
令 ans[u] 为最终答案,那么有 ans[1] = dp[1]。
现在我们要从 $1$ 开始换根。
比如说,我们已知了 $u$ 的答案 $ans[u]$,我们就可以理解成:整棵树,以 $u$ 作为root的答案已经求出来了,怎么求出 $to$ 的答案?
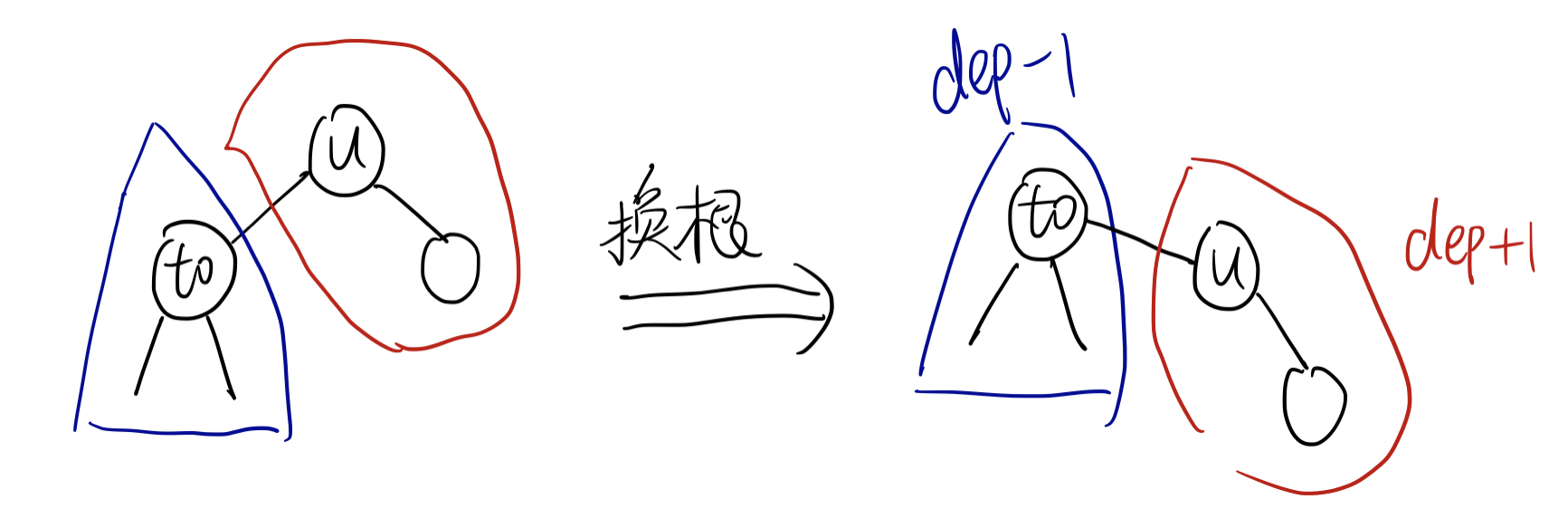
换根的过程是一个旋转的过程。我们把 $to$ 的子树向上旋转,将 $to$ 外面的部分($u$ 和其他的子树)向下旋转。
则,向上旋转的部分,对于答案贡献了 -sz[to](因为深度减少了),而向下旋转的部分,对于答案贡献了 (n-sz[to])。
所以,$ans[to] = ans[u] - sz[to] + (n - sz[to]);$
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int n, head[maxn], ecnt = 1;
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
ll sz[maxn], dp[maxn];
void dfs1(int u, int p) {
sz[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, u);
sz[u] += sz[to];
dp[u] += dp[to] + sz[to];
}
}
ll ans[maxn];
void dfs2(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
ans[to] = ans[u] - sz[to] + ((ll)n - sz[to]);
dfs2(to, u);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
dfs1(1, 0);
ans[1] = dp[1];
dfs2(1, 0);
ll maxans = 0, idx = 0;
for (int i = 1; i <= n; i++) {
if (ans[i] > maxans) {
maxans = ans[i];
idx = i;
}
}
cout << idx << endl;
}
例2 CF1324F Maximum White Subtree
题意
给定 $n$ 个节点的树,每个节点有一个值 $1$ 或者 $-1$。
对于每一个节点 $i$,求 $i$ 所在的连通块中,最大的节点权值和?
其中,$2 \leq n \leq 2 \times 10^5$
题解
首先固定 $1$ 为 root,进行一次DFS。
这样可以求出一个 dp[u]:代表以 $1$ 为root时,每个节点仅考虑其subtree,得到的最大值。
在第一次DFS的过程中,再维护一个数组 bool used[],其中 used[u] = 1 代表 $u$ 的parent $p$ 的答案用到了 $u$ 的这个subtree。
然后进行第二次DFS,计算出最终答案 ans[]。
首先有,ans[1] = dp[1]。
当我们在 dfs2(u) 时,在求一个child to 的答案 ans[to] 时,我们有两种选择:
-
to不使用外面的节点:$ans[to] = \max(ans[to], dp[to])$ -
to使用外面的节点:分两种情况讨论- 如果
to已经被包含在 $u$ 的答案中了(used[to] = 1),则 $ans[to] = \max(ans[to], ans[u])$ - 如果
to并没有被包含在 $u$ 的答案中,(used[to] = 0),那么to的最终答案,就是由 $to$ 的subtree 和 外面节点的合并而来。即 $ans[to] = \max(ans[to], ans[u] + dp[to])$
- 如果
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int n, head[maxn], ecnt = 1, val[maxn];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dp[maxn];
bool used[maxn]; // when calculating answer, whether used[u] is taken into consideration
void dfs1(int u, int p) {
dp[u] = val[u];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, u);
if (dp[to] > 0) dp[u] += dp[to], used[to] = 1;
}
}
int ans[maxn];
void dfs2(int u, int p) {
ans[u] = max(ans[u], dp[u]);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
if (used[to]) ans[to] = max(ans[to], ans[u]);
else ans[to] = max(ans[to], ans[u] + dp[to]);
dfs2(to, u);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> val[i];
if (val[i] == 0) val[i] = -1;
}
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
fill(ans, ans+maxn, -1e9);
dfs1(1,0);
dfs2(1,0);
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << endl;
}
例3 洛谷P6419 [COCI2014-2015#1] Kamp
题意
给定 $n$ 个节点的树。经过每条边都需要时间 $w_i$。
有 $K$ 个人,初始在 $K$ 个不同的点,他们要集中在一个点聚会。
聚会结束后,一辆车从聚会点出发(装上所有人),把这 $K$ 个人分别送回去。
求:如果聚会点在 $i$,则将这些人都送回去,所需最少的时间?
输出对于所有 $i = 1$ ~ $n$ 的结果。
其中,$1 \leq K \leq n \leq 5 \times 10^5, 1 \leq w \leq 10^8$。
题解
换根DP首先考虑:如果以 $1$ 作为根,怎么求出 $1$ 的答案?
• 以下,所有初始点我们都打上标记。
令 $sz[u]$ 为:$u$ 的 subtree(以 $1$ 为根的版本)中,标记点的数量。
令 $dp[u]$ 为:从 $u$ 出发,经过 $u$ 的 subtree(以 $1$ 为根的版本) 所有标记点,再回到 $u$,所需的最少时间(如果子树内无标记,则为0)。
那么通过第一次DFS,我们可以求出整个dp数组。
if (sz[to])
dp[u] += dp[to] + 2*w;
有了 $dp[1]$,我们还需要一个 $d[u]$,代表以 $u$ 为根的子树(以 $1$ 为根的版本)最长的链的长度。
同时我们再记录 $f[u]$:代表以u为根,包含了最长链的直接child $to$ 的编号。
最后 $1$ 对应的答案是:$dp[1] - d[1]$。(因为送到最长链,就不用再回到 $1$ 了)。
现在问题是,已知 $1$ 的答案,我们需要求出其他点的答案。
令 $ans[u]$ 为:从 $u$ 出发,经过整棵树的所有标记点,再回到 $u$,所需的最少时间。
易证 $ans[1] = dp[1]$。
然后进行第二次DFS,我们需要改变 $d[u]$ 的意义:此时 $d[u]$ 代表从 $u$ 出发的最长链的长度(以整棵树而言)。
同时,我们再维护一个数组 $s[u]$,代表从 $u$ 出发的第二长链的长度(以整棵树而言),并且第二长链必须和最长链 不在同一个子树内(这里的子树指,以 $u$ 为根的判断标准)。
我们在从 $u$ 转移到 $to$ 的时候,就有以下的几种情况:
-
$to$ 内无标记:
先从 $to$ 走到 $u$,访问所有的点,再从 $u$ 回到 $to$。
ans[to] = ans[u] + 2LL * w; d[to] = d[u] + w; // 现在,d[] 表示全局的链 -
$to$ 里面包含了整棵树的所有标记点:
最终答案就 等于 以 $to$ 为根,subtree的答案。
ans[to] = dp[to]; -
$to$ 里面包含了标记,外面也包含了标记:
那么对于整棵树而言,从 $to$ 出发,还是从 $u$ 出发都一样。所以
ans[to] = ans[u]。但是我们需要更新最长链和次长链。这个时候,我们就要分类讨论
f[u] = to与否。如果 $u$ 原本的最长链就不在 $to$ 的子树内,那么换根以后(旋转),$to$ 的最长链必然是 $to \rightarrow u \rightarrow f[u]$。
如果 $u$ 原本用到的最长链是 $to$,而旋转后,$to$ 的最长链就有可能用到 $u$ 的其他子树(除了 $to$ 以外的子树),所以我们需要维护次长链 $s[u]$,并且进行比较。
相应的,换根过程中,我们也要更新次长链 $s[to]$。
ans[to] = ans[u]; if (f[u] != to) { // 原本 to 不是最长,那么现在也必不可能是最长,所以 to 起点的最长链必然继承 u 原来的最长链 s[to] = d[to]; d[to] = w + d[u]; f[to] = u; } else { if (s[u] + w >= d[to]) { s[to] = d[to]; d[to] = s[u] + w; f[to] = u; } else if (s[u] + w > s[to]) { s[to] = s[u] + w; } }
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5+5;
int n, K, head[maxn], ecnt = 1;
bool tag[maxn];
struct Edge {
int to, nxt, w;
} edges[maxn<<1];
void addEdge(int u, int v, int w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
ll dp[maxn]; // dp[u]: 从u出发,只考虑其subtree中有标记的点,再回到u,得到的答案(如果子树内无标记,则为0)
ll ans[maxn]; // 从u出发,送完所有人,再回到u得到的答案
ll d[maxn]; // d[u]: 以u为根的子树内,最长的链的长度
ll s[maxn]; // s[u]: 以u为根的子树内,次长的链的长度 (不能和d所在的子树相同)
ll f[maxn]; // f[u]: 以u为根,包含了最深的有标记节点的to编号
int sz[maxn]; // sz[u]: 以u为根的subtree里的标记点数量
void chmax(int u, ll val) {
if (val > d[u]) {
s[u] = d[u];
d[u] = val;
} else {
if (val > s[u]) s[u] = val;
}
}
void dfs1(int u, int p) {
if (tag[u]) {
sz[u] = 1;
d[u] = 0;
s[u] = -1e15;
} else {
d[u] = s[u] = -1e15;
}
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
ll w = edges[e].w;
dfs1(to, u);
if (!sz[to]) continue; // 子树内无标记
dp[u] += dp[to] + 2LL*w;
sz[u] += sz[to];
if (d[to] + w >= d[u]) {
s[u] = d[u];
d[u] = d[to] + w;
f[u] = to;
} else if (d[to] + w > s[u]) {
s[u] = d[to] + w;
}
}
}
void dfs2(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (to == p) continue;
if (!sz[to]) { // to 里面没有标记点
ans[to] = ans[u] + 2LL * w;
d[to] = d[u] + w; // 现在,d[] 表示全局的链
} else if (K - sz[to] == 0) { // to 里面全是标记点
ans[to] = dp[to];
// 无需更新最长/次长链
} else { // 里外都有标记
ans[to] = ans[u];
if (f[u] != to) { // 原本 to 不是最长,那么现在也必不可能是最长,所以 to 起点的最长链必然出现在 u 所在的子树里
s[to] = d[to];
d[to] = w + d[u];
f[to] = u;
} else {
if (s[u] + w >= d[to]) {
s[to] = d[to];
d[to] = s[u] + w;
f[to] = u;
} else if (s[u] + w > s[to]) {
s[to] = s[u] + w;
}
}
}
dfs2(to, u);
}
}
int main() {
cin >> n >> K;
for (int i = 1; i <= n-1; i++) {
int u,v,w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
for (int i = 1; i <= K; i++) {
int a; cin >> a;
tag[a] = 1;
}
dfs1(1,0);
ans[1] = dp[1];
dfs2(1,0);
for (int i = 1; i <= n; i++) cout << ans[i] - d[i] << "\n";
}
例4 CF708C Centroids
题意
给定一个 $n$ 个节点的树,定义树的重心 $u$ 为:如果以 $u$ 为根,每个子树的大小都 $\leq \frac{n}{2}$。
现在,对于每个点 $u$,我们需要判断:
以 $u$ 为根时,能否在这棵树内,删去一条边,再添加一条边(不能加入已有的边),使得 $u$ 是重心?
其中,$2 \leq n \leq 4 \times 10^5$
题解
首先,如果一个节点本来就是重心,那么它的答案就是 $1$。
现在考虑,如果一个节点 $u$ 现在不是重心,怎么删边和加边,使得它成为重心?
我们会发现,如果以 $u$ 为根,对于 $u$ 的所有 neighbor $v$,有且仅有一个 $v$,使得 $v$ 所在的 subtree 的大小 $> \frac{n}{2}$, 那么我们就从这个 subtree $S_v$ 中,找到一个更小的subtree $S$,满足:
- $S$ 的大小 $\leq \frac{n}{2}$。
- $S$ 是 $S_v$ 内,所有满足条件中,最大的subtree。
然后我们把这个 subtree $S$ 断开,然后接到 $u$ 上,然后再判断一下 $u$ 此时是否为重心即可。
我们会发现,如果以 $u$ 为根,这样的 $S$ 其实很容易找到。现在要考虑换根的问题。
对于这道题而言,如果我们仅仅维护一个节点 $u$ 作为根时,subtree的信息,那么换根时会很麻烦。
我们需要额外维护一个信息 out[u],其中 $out[u]$ 就代表:以 $1$ 为根时,$u$ 所在子树 $S_u$ 外面的信息。
具体定义:$out[u]$ 代表:以 $1$ 为根时,设 $u$ 的parent为 $p$。然后令 $p$ 为根,除了 $S_u$ 以外的部分,满足大小 $\leq \frac{n}{2}$ 的最大子树。
然后就是 套路 里所说的:
先删去 $to$ 对于 $u$ 的贡献,再将 $u$ 加到 $to$ 上。
void dfs2(int u, int p) {
if (n - sz[u] > n/2) {
if (n - sz[u] - out[u] > n/2) ok[u] = 0;
}
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
if (n - sz[to] <= n/2) {
out[to] = n - sz[to];
} else {
// 删去 to 对于 u 的贡献(维护最大值,次大值 是常见套路了)
// 再把 u 加到 to 上去(更新 out[to])
if (use[u][0] == to) {
out[to] = max(out[u], dp[u][1]);
} else {
out[to] = max(out[u], dp[u][0]);
}
}
if (sz[to] > n/2) {
if (sz[to] - dp[to][0] > n/2) ok[u] = 0;
}
dfs2(to, u);
}
}
• 当然注意到上述代码,我们不一定要定义一个 $dp2[]$ 数组。这题的状态转移相对简单,所以直接将两步合成一步就可以了。下一题会用到较复杂的状态转移,此时就需要定义 $dp2[]$ 数组了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5+5;
int sz[maxn], head[maxn], ecnt = 1, dp[maxn][2], out[maxn], use[maxn][2], n;
bool ok[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void dfs1(int u, int p) {
sz[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs1(to, u);
sz[u] += sz[to];
if (sz[to] <= n/2) {
if (sz[to] > dp[u][0]) {
dp[u][1] = dp[u][0];
dp[u][0] = sz[to];
use[u][0] = to;
} else if (sz[to] > dp[u][1]) {
dp[u][1] = sz[to];
use[u][1] = to;
}
} else if (dp[to][0] > dp[u][0]) {
dp[u][1] = dp[u][0];
dp[u][0] = dp[to][0];
use[u][0] = to;
} else if (dp[to][0] > dp[u][1]) {
dp[u][1] = dp[to][0];
use[u][1] = to;
}
}
}
void dfs2(int u, int p) {
if (n - sz[u] > n/2) {
if (n - sz[u] - out[u] > n/2) ok[u] = 0;
}
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
if (n - sz[to] <= n/2) {
out[to] = n - sz[to];
} else {
if (use[u][0] == to) {
out[to] = max(out[u], dp[u][1]);
} else {
out[to] = max(out[u], dp[u][0]);
}
}
if (sz[to] > n/2) {
if (sz[to] - dp[to][0] > n/2) ok[u] = 0;
}
dfs2(to, u);
}
}
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
fill(ok, ok+maxn, 1);
dfs1(1, 0);
dfs2(1, 0);
for (int i = 1; i <= n; i++) {
cout << ok[i] << " ";
}
cout << endl;
}
例5 洛谷P3647 [APIO2014]连珠线
题意
现在有 $n$ 个珠子。珠子之间用线链接,每个线要么是红色,要么是蓝色。
我们将会从其中一个珠子开始(我们不知道这个珠子是哪个),每次用如下两种方式之一,添加珠子:
- 将一个 新的珠子 $w$ 和已经添加的珠子 $v$,用红线连起来。
- 将两个已经存在的珠子 $u,v$ 之间相连的红线删掉,然后添加一个 新的珠子 $w$ 使得 $(u,w)$,$(w,v)$ 用蓝线链接。
每条线都具有一个长度,游戏结束后,最终得分为蓝线长度之和。
给定游戏结束的局面(是一棵树),我们已知 珠子和线的连接方式,以及每条线的长度。但是我们不知道线的颜色。
求最大可能的得分?
其中,$1 \leq n \leq 2 \times 10^5$
题解
观察一下会发现,如果 $a,b$ 之间有蓝线,$b,c$ 之间也有蓝线。那么 $b$ 就是一个中间节点。这样的节点满足两个条件:
- $b$ 与 $a,c$ 一定是直接的neighbor。
- $b$ 只能作为一次中间节点(因为 $b$ 是通过第二种操作添加的新节点)
- $a,c$ 不能均为中间节点(因为 $a,c$ 之间,必须以红线相连,然后断开才行。这说明 $a,c$ 其中一个必须是通过第一种操作,得到的新珠子)
那么,在最终形成的树中,对于蓝线,有以下两种可能:
第一种情况:grandparent, parent, child
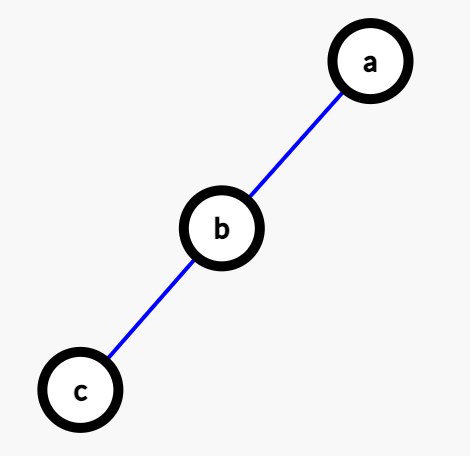
第二种情况:parent, child1, child2
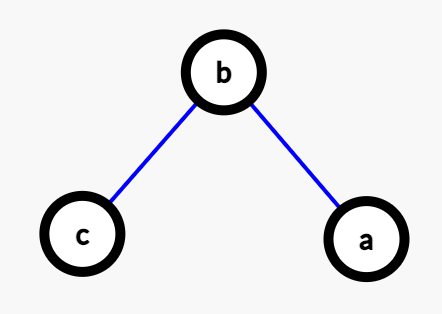
我们发现第二种情况很复杂,因为我们需要分类讨论 $a,c$ 是否本身为中间节点。
但是第一种情况,就比较好处理。我们只要加一个限定条件:
如果 $b$ 是中间节点(用 $1$ 来标记),那么它用蓝线相连的child $c$,就不能是中间节点(用 $0$ 来标记)。
等等,有两个疑问:
- 为什么我们限定的是蓝线相连的 child $c$?为什么不是parent $a$ ?
- 那如果第二种情况的那种出现了,怎么办?
这些问题都可以通过 固定 树的根来解决。
我们可以发现,如果我们设定树的根为: 最优解 中,最开始的那个珠子(虽然我们不知道它是哪一个),这些问题就都解决了。(比如第二个问题,我们可以保证这种情况不会出现)。
如上,我们只需要考虑第一种情况。那么,固定 $1$ 为根时,第一次 DFS 中,我们有:
设 $dp[u][0]$ 为:如果 $u$ 不是一个中间节点,那么它所在的subtree $S_u$ 中得到的蓝线长度最大和。
设 $dp[u][1]$ 为:如果 $u$ 是一个中间节点,那么它所在的subtree $S_u$ 中得到的蓝线长度最大和。
状态转移方程:
$$dp[u][0] = \sum\limits_{to} \max(w + dp[to][1], dp[to][0])$$
对于 $dp[u][1]$,因为它只能选择一个 child。它选择的那个child $v$,对它的贡献是 $w_{u,v} + dp[v][0]$,其他的child $to$ 的贡献都是 $\max(w + dp[to][1], dp[to][0])$。
所以只要把这个 $v$ 的贡献减去,再加上新贡献就可以了。
$$dp[u][1] = dp[u][0] + \max\limits_v \{ w+dp[v][0] - \max(w+dp[v][1], dp[v][0])\}$$
以 $1$ 为根的情况有了,现在考虑一下换根?
由换根套路,首先将 $to$ 对于 $u$ 的影响删去(基于 $ans[u]$),有:
$$dp2[u][0] = ans[u][0] - \max(w + dp[to][1], dp[to][0])$$
然后,对于 $dp2[u][1]$,我们分类讨论一下 $to$ 是否为 $u$ 的最佳转移点(也就是说,$ans[u][1]$ 是否用到了 $to$,作为最大值)。
$$dp2[u][1] =
\begin{cases}
ans[u][1] - maxval[u][0] + maxval[u][1] & \text{If to 是 u 的最佳转移点} \\
ans[u][1] & \text{Otherwise}
\end{cases}$$
然后,再基于 $dp[to]$ 的基础上,将 $dp2[u]$ 作为 child 给 $to$ 的影响加到 $to$ 上即可。
最后,答案就是 $\max\limits_u \{ans[u][0]\}$。(因为 $ans[u][1]$ 并没有意义,$u$ 作为根的时候是没有parent的)。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
struct Edge {
int to, w, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1, n, dp[maxn][2], dp2[maxn][2], ans[maxn][2]; // dp: 以 1 为根, dp2: 换根后, ans: 最终答案
int use[maxn][2], maxval[maxn][2]; // use[u]: 转移时,所用的前两大的值,对应的两个vertex; maxval[u] : 转移时所用的前两大的值
void addEdge(int u, int v, int w) {
Edge e = {v, w, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
void dfs1(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to, w = edges[e].w;
if (to == p) continue;
dfs1(to, u);
dp[u][0] += max(w + dp[to][1], dp[to][0]); // 转移 dp[u][0]
// 转移 dp[u][1]
int val = w + dp[to][0] - max(w + dp[to][1], dp[to][0]);
if (val > maxval[u][0]) {
maxval[u][1] = maxval[u][0];
use[u][1] = use[u][0];
maxval[u][0] = val;
use[u][0] = to;
} else if (val > maxval[u][1]) {
maxval[u][1] = val;
use[u][1] = to;
}
}
dp[u][1] = dp[u][0] + maxval[u][0];
}
void dfs2(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to, w = edges[e].w;
if (to == p) continue;
// 删去 to 对于 u 的影响,基于 ans[u],得到 dp2[u]
dp2[u][0] = ans[u][0] - max(w + dp[to][1], dp[to][0]);
if (to == use[u][0]) {
dp2[u][1] = ans[u][1] - maxval[u][0] + maxval[u][1];
} else {
dp2[u][1] = ans[u][1];
}
dp2[u][1] -= max(w + dp[to][1], dp[to][0]);
// 将 dp2[u] 作为 child,重新加给 to(在 dp[to] 的基础上),作为新的 child
ans[to][0] = dp[to][0] + max(w + dp2[u][1], dp2[u][0]);
int val = w + dp2[u][0] - max(w + dp2[u][1], dp2[u][0]);
if (val > maxval[to][0]) {
maxval[to][1] = maxval[to][0];
use[to][1] = use[to][0];
maxval[to][0] = val;
use[to][0] = u;
} else if (val > maxval[to][1]) {
maxval[to][1] = val;
use[to][1] = u;
}
ans[to][1] = ans[to][0] + maxval[to][0];
dfs2(to, u);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n-1; i++) {
int u,v,w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
for (int i = 1; i <= n; i++) maxval[i][0] = maxval[i][1] = -1e9; // 注意初始化,否则会有问题
dfs1(1, 0);
ans[1][0] = dp[1][0], ans[1][1] = dp[1][1];
dfs2(1, 0);
int maxans = 0;
for (int i = 1; i <= n; i++) maxans = max(maxans, ans[i][0]); // 注意这里是 ans[i][0]
cout << maxans << endl;
}
例6 CF1725J Journey
题意
给定一棵树,每条边有边权,现在我们可以从任意节点出发,需要访问每个节点至少一次。
在访问过程中,我们拥有一次使用传送门的机会,使得我们可以从一个节点无损耗的传送到另外一个节点。
求访问每个节点至少一次,并且至多使用一次传送门的最小消耗?
其中,$n \leq 10^5$。
题解
先考虑一下,如果我们不能使用传送门怎么算?
我们假设从 $x$ 出发,可以看作树以 $x$ 为根,那么每次走完一个子树都要回到 $x$,如果我们的路径最后停留在 $y$,说明 $(x,y)$ 这条路径仅被访问一次,而其他的边都会被访问两次。
所以对于整棵树而言,我们希望 $(x,y)$ 这条路径尽可能长,也就是这棵树的直径。然后对于其他的边,都访问了两次。所以答案就是:设 $sum$ 为所有边权和,$D$ 为直径长度,答案为 $2 * sum - D$。
好的,接下来考虑有传送门的情况。
有两种情况:
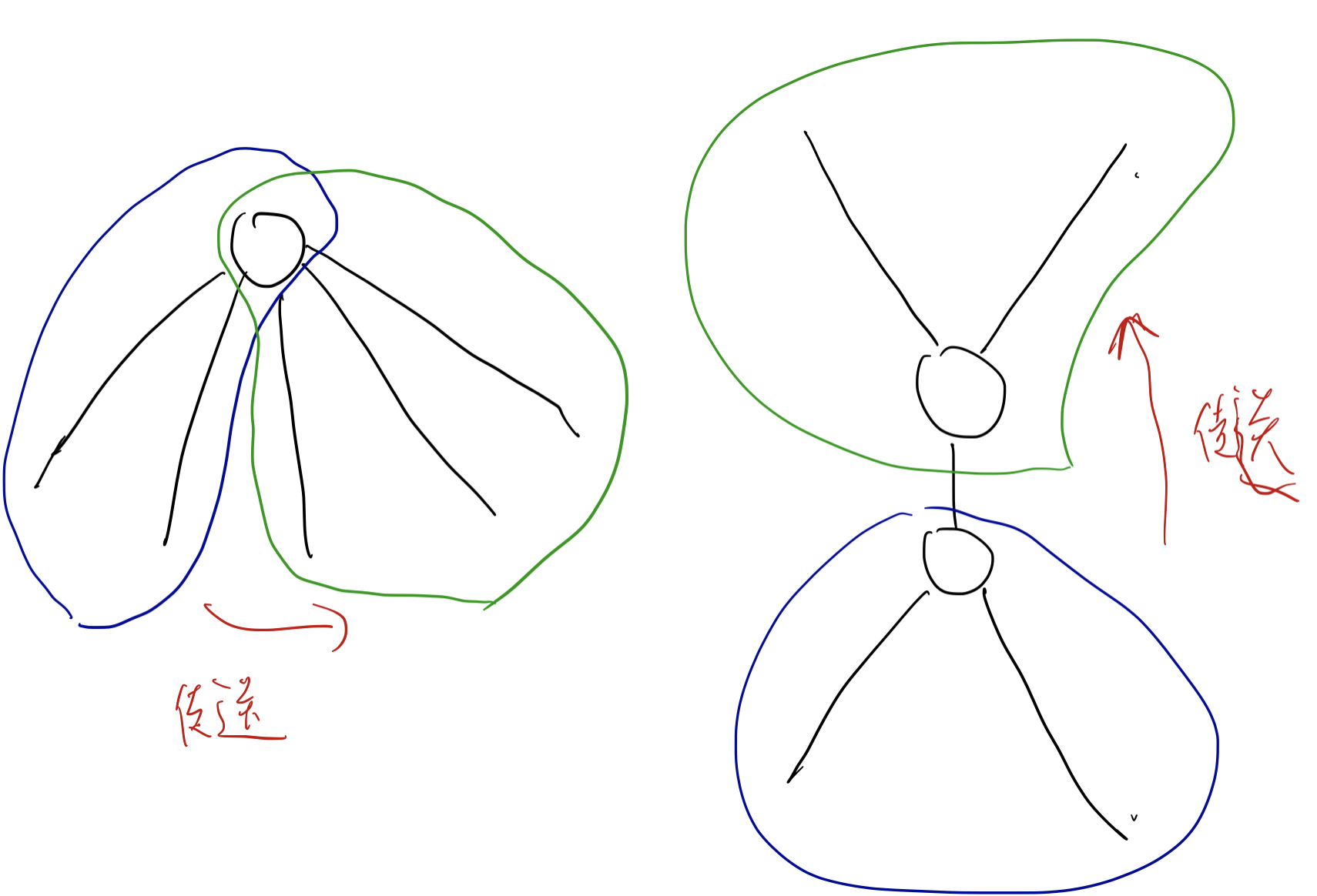
第一种是在 $u$ 为根的情况,从 $u$ 的其中一个子树中走一圈,然后传送到 $u$ 的另外一个子树中走一圈,每条边都至少被用过一次。
第二种 $u$ 不是根的情况,设 $u$ 的parent为 $p$,那么先从 $u$ 的子树中走一圈,然后传送到除了 $u$ 的子树以外的位置走一圈,这样这条边 $(p, u)$ 就没有被用到。
对于第一种情况,以 $u$ 为起点的四条最长链只被访问一次,剩下的都是 $2$ 次,所以只要计算当 $u$ 作为根时,它作为起点的四个最长链(并且不相交,位于不同子树内)的长度。
对于第二种情况,相当于把一条边割开,然后得到两个分开的子树,这就是两个子树的子问题了,相当于两个子树内走一圈,无法使用传送门,所以只要求两个子树的直径即可。
注意到,我们需要对每一个 $u$ 都讨论第一种情况,对于每一条边都讨论第二种情况,这可以通过换根 dp 解决。
我们先明确我们需要求的内容 (以下均为 $1$ 作为根时讨论)
dia[u]: $u$子树(包括u)的最长直径。
dp1[u][3]: $u$子树内,以u为起点的最长链 (前 $3$ 长)长度。
dp2[u][2]: $u$子树内(不包括 u),最长(前 $2$ 长)的直径长度。
len[u]: $(u, par[u])$ 的权值。
up1[u]: $u$外面(整棵树去掉 $u$ 子树后),以 $par[u]$ 作为起点的最长链。
up2[u]: $u$外面(整棵树去掉 $u$ 子树后)的最长直径。
有了这些信息,所有问题都可以解决,现在看下怎么求这些信息?
首先是 dia[u]:
这是一个常规的树形 DP 问题,
$u$ 子树的直径有两种情况,要么经过了 $u$,要么完全位于 $u$ 的子树里面。
对于第一种情况,求出以 $u$ 为起点的前 $2$ 个最长链,然后相加即可,这个就是 dp1[u][0] + dp1[u][1],很好求。
对于第二种情况,求出 dp2[u][0] 即可.
然后是 up1[],我们看下图,这是正在求 up1[v] 的过程。
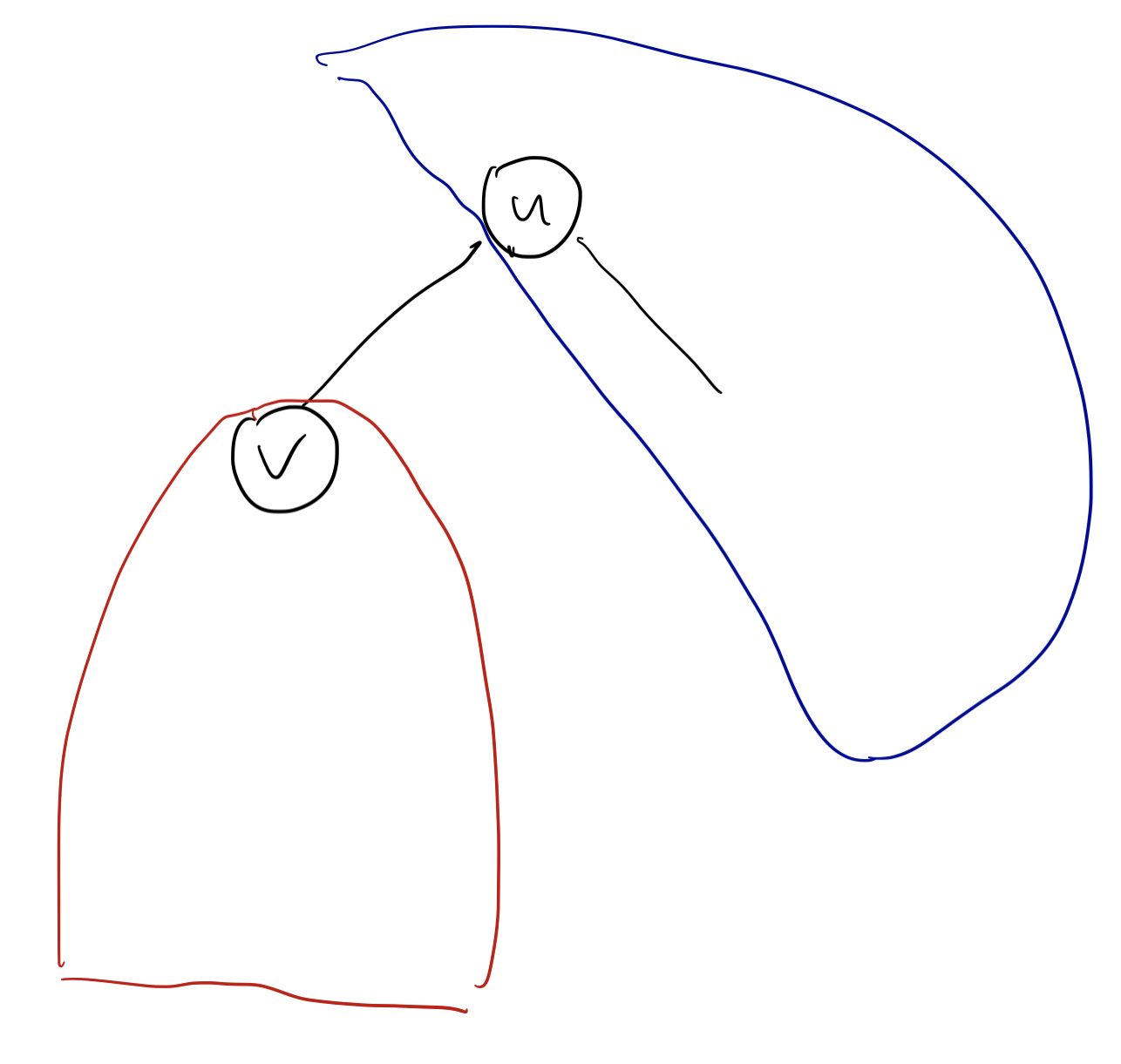
有两种情况:
- $u$ 为起点的最长链经过了 $v$。
- $u$ 为起点的最长链没有经过 $v$。
第一种情况下,up1[v] = max(up1[v], dp1[u][1])。
第二种情况下,up1[v] = max(up1[v], dp1[u][0])。
接下来是 up2[],同样按照上图求 up2[v] 的过程进行分类讨论:
有两种情况:
- $u$ 的子树内的直径经过了 $u$。
- $u$ 的子树内的直径没经过 $u$。
第一种情况下,使用的是 dp1[u][0] + dp1[u][1],所以只要判断 $v$ 贡献了 dp1[u][?] 即可,比如如果 $v$ 贡献了 dp1[u][1],那么就让 up2[v] = max(up2[v], dp1[u][0] + dp1[u][2]),即贡献来自其余两个链。
第二种情况下,使用的子树的直径,也就是 dp2[u][?],判断是否有 dia[v] == dp2[u][0],如果有,就用 up2[v] = max(up2[v], dp2[u][1]),否则用 up2[v] = max(up2[v], dp2[u][0])。
除此之外,我们还需要换根。也就是在更新 up1[v], up2[v] 之前,要先把 $u$ 看作为根,所以需要把 $u$ 的parent那条链旋转下来,然后更新 dp1[u], dp2[u]。
上面解决了问题 $2$,切分子树,然后要解决问题一:找四条最长不相交链的问题。
这个只要对每个节点维护一个大小为 $4$ 的最小堆即可,在第一次 dfs 的时候找到所有子树的最长链插入堆中,然后在将 up1[u] + len[u] 也就是 parent 的最长链插入即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n;
struct Edge {
int to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v, int w) {
Edge e = {v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dia[maxn]; // dia[u]: u子树(包括u)的最长直径
ll dp1[maxn][3]; // u子树内,以u为起点的最长链长度
ll dp2[maxn][2]; // u子树内(不包括 u),最长的直径长度
int len[maxn]; // len[u]: w(u, par[u])
ll up1[maxn]; // u外面(整棵树去掉 u子树后)的最长链
ll up2[maxn]; // u外面(整棵树去掉 u子树后)的最长直径
ll sum = 0; // 所有 w 的和
priority_queue<ll, vector<ll>, greater<ll>> chain[maxn]; // chain[u]: 记录以u为起点的前4长的链
void dfs1(int u, int p) {
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to, w = edges[e].w;
if (v == p) continue;
len[v] = w;
sum += w;
dfs1(v, u);
// 更新 dp1[u]
ll t = w + dp1[v][0];
for (int j = 0; j <= 2; j++) {
if (t >= dp1[u][j]) swap(t, dp1[u][j]);
}
// 更新 dp2[u]
t = dia[v];
for (int j = 0; j <= 1; j++) {
if (t >= dp2[u][j]) swap(t, dp2[u][j]);
}
dia[u] = max({dia[u], dp1[u][0] + dp1[u][1], dp2[u][0]});
// 最后记录 chain[u]
chain[u].push(w + dp1[v][0]);
if (chain[u].size() > 4) chain[u].pop();
}
}
ll ans = 0;
void dfs2(int u, int p) {
// // 此时需要先把 u 外面的那条链转过来,更新 dp1[u]
ll t = len[u] + up1[u];
for (int j = 0; j <= 2; j++) {
if (t >= dp1[u][j]) swap(t, dp1[u][j]);
}
// 同理更新 dp2[u]
t = up2[u];
for (int j = 0; j <= 1; j++) {
if (t >= dp2[u][j]) swap(t, dp2[u][j]);
}
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to, w = edges[e].w;
if (v == p) continue;
// 更新 up1[v]
if (w + dp1[v][0] == dp1[u][0]) { // 如果u子树内最长链用到了 v
up1[v] = max(up1[v], dp1[u][1]);
} else {
up1[v] = max(up1[v], dp1[u][0]);
}
// 更新 up2[v]
// Case1: 直径经过 u
if (dp1[v][0] + w == dp1[u][0]) {
up2[v] = max(up2[v], dp1[u][1] + dp1[u][2]);
} else if (dp1[v][0] + w == dp1[u][1]) {
up2[v] = max(up2[v], dp1[u][0] + dp1[u][2]);
} else {
up2[v] = max(up2[v], dp1[u][0] + dp1[u][1]);
}
// Case2: 直径没经过 u
if (dp2[u][0] == dia[v]) {
up2[v] = max(up2[v], dp2[u][1]);
} else {
up2[v] = max(up2[v], dp2[u][0]);
}
ans = min(ans, sum * 2 - w * 2 - dia[v] - up2[v]);
dfs2(v, u);
}
}
int main() {
cin >> n;
for (int i = 1; i < n; i++) {
int u, v, w; cin >> u >> v >> w;
addEdge(u, v, w); addEdge(v, u, w);
}
dfs1(1, 0);
ans = sum * 2;
dfs2(1, 0);
for (int u = 1; u <= n; u++) {
chain[u].push(up1[u] + len[u]);
if (chain[u].size() > 4) chain[u].pop();
ll res = 0;
while (chain[u].size()) {
res += chain[u].top();
chain[u].pop();
}
ans = min(ans, sum * 2 - res);
}
cout << ans << endl;
}
例7 CF1796E. Colored Subgraphs
题意
有一棵 $n$ 个节点的树,现在我们可以选择任意一个节点 $r$ 作为树的根,然后将所有节点染色,每个节点染什么色由我们决定,无任何限制。
一个好的染色方案要求满足以下两点:
- 每两个相同颜色 $c$ 的节点 $u,v$ 之间的路径上的所有节点的颜色均为 $c$。
- 对于任意两个相同颜色的节点 $u,v$,它们的深度不相等。
对于每一种颜色,统计这个颜色有多少个节点,我们对每一种颜色的 count 取最小值,作为这个染色方案的 cost。
求所有好的染色方案的 cost 的最大值?
其中,$n \leq 2 \times 10^5$。
题解
显然,将 $r$ 作为根以后,每个颜色必然是一条链,并且这条链是一条从上往下的。现在我们需要让每条链的节点数量的最小值最大。
考虑换根dp:
令 $f_u$ 为:在 $u$ 的子树内,尚未结束的最短链的长度。
令 $g_u$ 为:在 $u$ 的子树内,已经结束的最短链的长度。
• 一棵子树内,有且仅有一个尚未结束的最短链,因为尚未结束意味着这条链包含了 $u$ 本身,子树内的其他所有链都已经结束了。
转移时,显然会选择所有的children中,尚未结束的链中最短的那个,接到节点 $u$ 上,作为这个子树的尚未结束的链,而剩下的所有链都会变成已经结束的链。
所以转移方程有:
$$f_u = \min_v \{f_v \} + 1$$
$$g_u = \min \{ \min_v \{g_v \} , \min_{v \neq x} \{ f_v\} \}$$
其中,$v$ 是 $u$ 的children,而 $x$ 是第一个式子转移时用到的 $v$(也就是所有children里 $f_v$ 最小的)。
对于以 $r$ 为根的树,答案就是 $\min \{f_r, g_r \}$。
现在考虑换根。
假设我们知道了以 $p$ 为根的结果,现在 $u$ 是 $p$ 的一个child,要转移到 $u$ 为根的结果,怎么做?
按照经典套路:
- 先将 $u$ 的子树从 $p$ 里面扣掉。
- 将扣掉 $u$ 后的 $p$ 作为一棵子树,加进 $u$ 里面。
虽然一般我们是维护次大值之类的,然后开始疯狂分类讨论,不过直接用 set 来做,多加一个log,更好写。
最后注意:
-
在将 $u$ 的子树从 $p$ 里面扣掉时,需要注意不能直接修改 $p$ 对应的 set,因为 $p$ 对应的 set 储存的是以 $p$ 为根时的信息,换其他根的时候可能还会用到,所以需要手动进行模拟,求出 $p$ 删掉 $u$ 以后的信息。
-
在将扣掉 $u$ 后的 $p$ 作为子树加进 $u$ 里面时,需要修改 $u$ 的set(因为set维护的是以 $u$ 为根的信息)。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
vector<int> adj[maxn];
int n, dp[maxn], dp2[maxn];
set<pii> se1[maxn], se2[maxn]; // (dp_val, v), (dp2_val, v)
void dfs(int u, int p) {
dp[u] = dp2[u] = 1e9;
for (int v : adj[u]) {
if (v == p) continue;
dfs(v, u);
dp[u] = min(dp[u], dp[v] + 1);
dp2[u] = min(dp2[u], dp2[v]);
se1[u].insert({dp[v], v});
se2[u].insert({dp2[v], v});
}
if (se1[u].size() > 1) {
dp2[u] = min(dp2[u], next(se1[u].begin())->first);
}
if (dp[u] == 1e9) dp[u] = 1;
}
int ans = 0;
void dfs2(int u, int p) {
if (u != 1) { // 从 p 开始转移
// 将 p 中,关于 u 的信息去掉
int sz = se1[p].size();
int d1 = 1e9, d2 = 1e9;
if (se1[p].begin()->second == u) {
if (sz > 1) {
d1 = next(se1[p].begin())->first + 1;
} else d1 = 1;
} else {
d1 = se1[p].begin()->first + 1;
}
if (se2[p].begin()->second == u) {
if (sz > 1) d2 = next(se2[p].begin())->first;
} else {
d2 = se2[p].begin()->first;
}
int f = se1[p].begin()->second; // 应该是去掉以后的second
if (f == u && se1[p].size() > 1) f = next(se1[p].begin())->second;
auto itr = se1[p].begin();
while (itr != se1[p].end() && (itr->second == f || itr->second == u)) {
itr = next(itr);
}
if (itr != se1[p].end()) {
d2 = min(d2, itr->first);
}
// 然后将 p 插入到 u 中
se1[u].insert({d1, p});
se2[u].insert({d2, p});
dp[u] = se1[u].begin()->first + 1;
dp2[u] = se2[u].begin()->first;
if (se1[u].size() > 1) {
dp2[u] = min(dp2[u], next(se1[u].begin())->first);
}
}
ans = max(ans, min(dp[u], dp2[u]));
for (int v : adj[u]) {
if (v == p) continue;
dfs2(v, u);
}
}
void solve() {
cin >> n;
ans = 0;
for (int i = 1; i <= n; i++) adj[i].clear(), se1[i].clear(), se2[i].clear();
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 0);
dfs2(1, 0);
cout << ans << "\n";
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
