二分图 & 二分图匹配
Contents
二分图 - 定义
二分图是一种特殊的无向图,可以将点集划分为两部分,在同一集合中的节点之间没有 edge。
二分图 - 性质
- 二分图 $\iff$ 图中没有奇环(指节点个数为奇数的环) $\iff$ 可以进行二分图染色
二分图染色
给定一个二分图,我们可以仅用两种颜色将每个节点染上色,并且保证每个 edge 的两端颜色一定不同。
同理,如果一个图可以进行二分图染色,那么它就是一个二分图(这用于 判断一个图是否为二分图)
染色的方法:用 DFS 即可。(记得要从每个节点都开始 DFS 一次)
- 随机选择一个点 $u$ 作为出发点,它的颜色为 $c_u = 0$。
- 看它的 neighbor $v$ 的颜色,如果等于 $c_u$ ^ $1$,或者没染色,就染成 $c_u$ ^ $1$。否则的话产生冲突,说明这不是二分图。
模型转化
网格二分图
一个常见的套路,$n \times m$ 的矩阵中,某些格子之间有冲突(比如相邻的格子)。我们按照格子 $(i,j)$ 的和 $(i+j)$ 的奇偶性 将格子分为左部分的点和右部分的点,冲突的连边。
• 在二分图匹配时,一定要分成左右两边的点,并且从左边的点连 单向边 到右边的点。
例题
例1 CF741C Arpa’s overnight party and Mehrdad’s silent entering
题意
给定 $n$ 对情侣 $(a_i, b_i)$($a_i, b_i \in [1,2n]$),总共有 $2n$ 个人,每个人的编号是从 $1$ 到 $2n$。现在有 $2$ 种食物($1$ 或者 $2$),求一种分配方式使得:
- 每对情侣 $(a_i, b_i)$ 不能吃同一种食物。
- 相邻的 $3$ 个编号,食物不能完全相同。(编号是环形的,这意味着 $2n, 1, 2$ 也算是相邻的 $3$ 个人)。
如果无解,输出 $-1$。
其中,$1 \leq n \leq 10^5$。
题解
每对情侣 $(a_i, b_i)$ 的食物不同,让我们想到二分图。但是第二个条件怎么办?
直觉上来说,这个题一定是有解的。
所以,我们可以做一个特殊的限制,直接强制 $2i-1, 2i$ 的食物不同,这个条件就满足了。
接下来我们要证明,将第二个限制条件转化以后,仍然有解。
对于这个模型建图,将每个人作为一个节点,每对情侣 $(a_i, b_i)$ 作为一条边连起来。然后再将 $(2i-1, 2i)$ 作为一条边连起来。
那么只要这个图是二分图,就有解。(因为二分图保证了每条边两端的颜色不同)
如果图中有环,那么必然是由 $x$ 对情侣组成的一个环。所以环的节点数量为 $2x$。所以不可能有奇环。所以这个图是二分图。
所以建完图以后,跑一个二分图染色即可。
• 注意,二分图染色的 DFS 要从每一个节点都开始一次。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
const int maxm = 1e6;
int n;
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
int color[maxn];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
edges[ecnt] = e;
head[u] = ecnt++;
}
int a[maxn], b[maxn];
bool vis[maxn];
void dfs(int u) {
if (vis[u]) return;
vis[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
color[to] = color[u] ^ 1;
dfs(to);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i] >> b[i];
addEdge(a[i], b[i]);
addEdge(b[i], a[i]);
}
for (int i = 1; i <= 2*n; i+=2) {
addEdge(i, i+1);
addEdge(i+1, i);
}
vis[1] = 1;
for (int i = 1; i <= 2*n; i++) dfs(i);
for (int i = 1; i <= n; i++) {
if (!color[a[i]]) cout << 2 << " ";
else cout << 1 << " ";
if (!color[b[i]]) cout << 2 << "\n";
else cout << 1 << "\n";
}
}
例2 CF553C Love Triangles
题意
给定 $n$ 个人,每两个人之间,要么互相love,要么互相hate。
现在已知 $m$ 个关系,每个关系的格式为 $a ~ b ~ c$,代表 $a$ 和 $b$ 互相 love($c = 1$),或者互相 hate($c = 0$)。
请求出,有多少个方案使得整个关系网满足以下条件(答案对 $10^9+7$ 取模)
对于任意三个人 $a,b,c$,要么这三个人互相 love,要么 $a,b$ 互相love,而 $a,c$ 和 $b,c$ 互相hate。
其中,$3 \leq n \leq 10^5, 0 \leq m \leq 10^5$
题解
首先我们会发现,love是有传递性的:如果 $a,b$ 互相love,$b,c$ 互相love,那么根据定义,一定有 $a,c$ 互相love。
所以对于love的关系,我们可以求出一个连通块,使得这个块内每个人互相love,那就可以缩点了。(当然需要注意的是 hate 不具有传递性)。
于是,我们只需要考虑一下 hate 怎么处理。
先放一个结论:
如果我们把这个问题考虑为图染色问题,那么两个互相hate,说明颜色不同。而互相love,说明颜色相同。
如果存在一个合法的染色方式,则说明有解。(本质上是二分图染色,互相love的在同一侧,互相hate的在两侧)
证明:存在染色方式 $\rightarrow$ 有解:
任取三个节点 $a,b,c$,有两种情况:
- $a,b,c$ 在同一侧,所以满足 $a,b,c$ 互相love。
- $a,b$ 在同一侧,$c$ 在另外一侧。这也刚好满足了 $a,b$ 互相love,而 $a,c$ 和 $b,c$ 互相hate。
证明:有解 $\rightarrow$ 存在染色方式:
根据定义染色即可,我们会发现没有冲突情况。
方案数怎么计算?
我们先进行 DFS,求出图中的连通块。
如果每个连通块内,都没有冲突情况(也就是说,每个连通块都可以做二分图染色)的话,说明有解,否则无解($ans = 0$)。
同时我们发现,对于任何一个连通块,我们只要给其中一个节点染上色,这个连通块内的其他所有节点的颜色也都确定了。
所以我们只需要给每个连通块染色即可。
设连通块的数量为 $c$,那么答案就是 $2^{c-1}$。
• 为什么不是 $2^c$?我们只要确定了第一个块的颜色,剩下的 $(c-1)$ 个块随便选颜色。我们答案是否合法,实际上与第一个块的颜色无关。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n,m;
int head[maxn], ecnt = 1, color[maxn];
struct Edge {
int to, nxt, w;
} edges[maxn<<1];
void addEdge(int u, int v, int w) {
Edge e = {v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll ans = 1;
void dfs(int u) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to, w = edges[e].w;
if (color[to] >= 0) {
if (color[to] != (color[u] ^ w ^ 1)) ans = 0;
} else {
color[to] = (color[u] ^ w ^ 1);
dfs(to);
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u,v,w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
}
fill(color, color+maxn, -1);
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (color[i] == -1) {
cnt++;
color[i] = 0;
dfs(i);
}
}
cnt--;
for (int i = 1; i <= cnt; i++) {
ans = ans * 2LL % mod;
}
cout << ans << "\n";
}
二分图匹配 - 定义
一个 匹配 的定义是一个 边集,并且这个边集中,每两个边之间没有共同的顶点。二分图的最大匹配是指 边的数量 最多的一个匹配。
二分图匹配常用的算法是 匈牙利算法 $O(nm)$,或者 最大流(dinic的复杂度为 $O(\sqrt n m)$。
匈牙利算法求最大匹配
匈牙利算法本质上是一个个求增广路(增广路指的是 从左开始,到右结束的路径,其中 左 $\rightarrow$ 右都是未匹配边,右 $\rightarrow$ 左都是匹配边)的过程。
如果我们以男女配对为例子:
对于每一个男生 $i$($i$ 在二分图的 左侧点集 中),遍历他每一个心仪的女生 $j$ ($j$ 在二分图的 右侧点集 中)(这说明 $(i,j)$ 是一条边)。那么有两种情况:
- 女生 $j$ 未配对,那么他们两个就配对在一起,
match[j] = i。 - 女生 $j$ 已配对,那么就让女生 $j$ 去问一下她当前的男朋友
match[j],让她男朋友尝试再换一个新的女朋友(所以就变成一个新的男生尝试配对,那么这就是一个递归的过程)。如果她男朋友成功换掉了女朋友,那么这个男生 $i$ 就可以和 女生 $j$ 配对了。否则 $i$ 就只能单着。
代码片段如下:
int n, m, adj[maxn][maxn];
int match[maxn], vis[maxn], id = 0;
// match[j] 代表女生j 当前的男朋友 i, vis[j] 代表这个女生在当前男生 i 的配对过程中,是否访问过了
bool dfs(int i) {
for (int j = 1; j <= m; j++) {
if (!adj[i][j] || vis[j] == id) continue;
vis[j] = id;
if (!match[j] || dfs(match[j])) {
match[j] = i;
return 1;
}
}
return 0;
}
int main() {
int ans = 0;
for (int i = 1; i <= n; i++) {
id++;
ans += dfs(i);
}
}
有几个需要注意的点:
- 利用
int vis[]来代表这个女生 $j$ 在当前男生 $i$ 的配对过程中,是否访问过了。(因为对于每个男生 $i$ 而言,对于每个女生 $j$ 只需要问一次即可)。 - 利用
id来记录这是第几次 $dfs(i)$,然后只要判断 $vis[j]$ 是否等于 $id$ 就可以判断,本次 DFS 中是否询问过女生 $j$ 了。(这样就不用每次 DFS 结束都memset()一次)。
时间复杂度:每个男生都要询问所有女生,所以是 $O(nm)$(这里 $n$ 代表左边点集的数量,$m$ 代表右边点集)。
最大匹配,最小点覆盖,最大独立集,最小边覆盖
以下的 $N$ 指所有节点的数量,就是左节点和右节点的数量和。
最小点覆盖
定义:选择一个最小的点集 $S\subset V$ 使得每一条边至少有一个端点在 $S$ 中。
性质:最小点覆盖 $=$ 最大匹配。
构造方法:从左边的每一个非匹配点(且未打上标记的)出发,沿着非匹配边正向(从左往右)进行遍历,沿着匹配边反向(从右往左)进行遍历。遍历到的所有点进行标记。
选取左部分中没有被标记过的点,右部分中被标记过的点,则这些点可以形成该二分图的最小点覆盖。
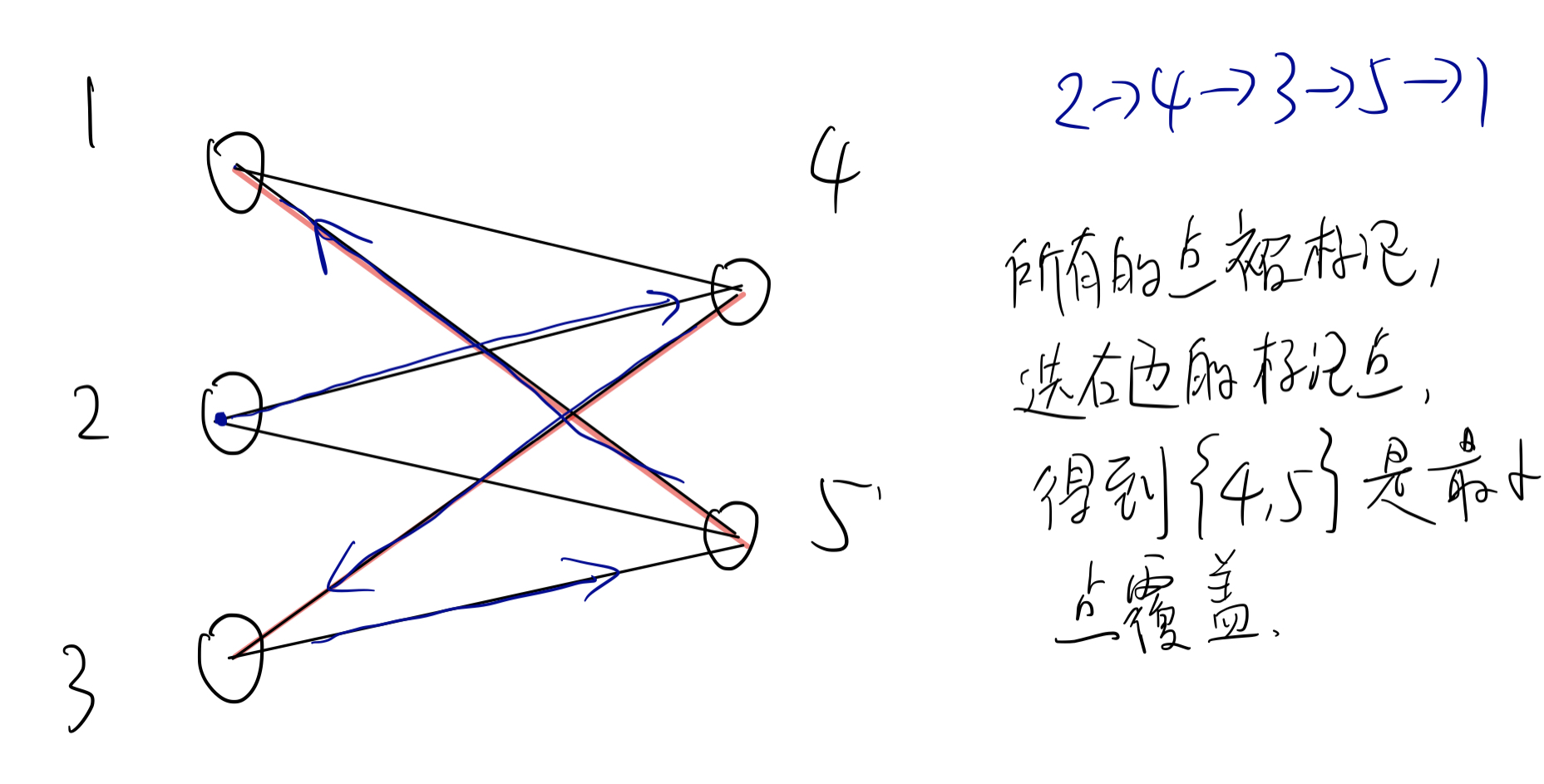
证明:
- 这个集合的大小等于最大匹配
一条匹配的边两侧一定都有标记(在增广路上)或都没有标记(不在增广路上),如果有标记,右边的点会被算进去,没有标记的话,左边的点会被算进去,无论如何答案等于最大匹配。
- 所有边都被覆盖到了
对于匹配边,肯定有一个端点被选中了(理由同上)。对于没有匹配的边,它一定会成为增广路的一部分(如果没有,说明增广路遍历过程尚未结束)。
- 它是最小的点覆盖
为了覆盖所有边,不可能比最大匹配更小了,否则违反了最大匹配的定义。
最大独立集
定义:选择一个最大的点集 $S \subset V$,使得 $\forall u,v \in S$,$(u,v)$ 之间没有边。
性质:最大独立集 $= N -$ 最大匹配。
构造方法:直接求最小点覆盖,然后取补集即可。
证明:我们考虑一下每条边 $(u,v)$,根据定义,$u,v$ 中至少有一个在最小点覆盖中,所以 $u,v$ 中最多只能有一个在最小点覆盖的补集中。
所以最小点覆盖的补集两两之间没有边。
最小边覆盖
定义:选择一个最小的边集 $A \subset E$,使得这些边能够覆盖到所有的点。
性质:最小边覆盖 $= N - $ 最大匹配。
构造方式:设最大匹配为 $M$。先取所有的匹配边,每次能解决 $2$ 个点。对于剩下的没覆盖的点,随便取它的一条非匹配边来覆盖它。
证明:根据以上构造,匹配边选了 $M$ 条,非匹配边选了 $N-2M$ 条。总共是 $M + N-2M = N-M$。
Hopcroft-Karp 算法求二分图匹配
我们提到了二分图匹配可以用网络流来 $O(m\sqrt n)$ 的做,但这样不好输出方案,还不好写,但是我们有一个 HK 算法可以在同样的时间复杂度解决这个问题,并且好写。
大体思路和匈牙利算法一样,只不过限定了只增广最短路,大致分为三步:
- 从所有未匹配的左点出发,进行 bfs,求出所有左点的距离。这个bfs过程中,不能经过未匹配的右点(所以只能走增广路)
- 和匈牙利算法一样进行 dfs 增广,但只能走 $d_v = d_u + 1$ 的增广路(其中 $u,v$ 均为左点)
- 重复,直到无法继续增广。
时间复杂度:$O(m\sqrt n)$,因为最多增广 $O(\sqrt n)$ 次。
证明:见 这里。
大致思想:利用了 “每一轮增广路的长度都比上一轮要长“ 的结论,先跑 $O(\sqrt n)$ 轮将长度 $\leq \sqrt n$ 的增广路都跑完了,并且增广路长度 $> \sqrt n$ 的路径最多只有 $O(\sqrt n)$ 条,因为最大匹配所需要的边最多是 $O(n)$ 级别的。
• 顺带一提,这个方法能够很方便的求出最小点覆盖的方案,但原理我没搞清楚。
• 测试 $n=10^5$ 情况的板子:链接
代码
const int maxn = 1e5+5;
struct HopcroftKarp {
int n, m, res = 0; // n: 左点数,m: 右点数, res: 最大匹配
int lmatch[maxn], rmatch[maxn], dis[maxn]; // lmatch[u] -> v, rmatch[v] -> u
vector<int> adj[maxn];
HopcroftKarp(int n, int m): n(n), m(m) {
memset(dis, -1, sizeof(dis));
}
void addEdge(int u, int v) {
adj[u].push_back(v);
}
void bfs() {
queue<int> q;
for (int i = 1; i <= n; i++) {
if (!lmatch[i]) {
q.push(i), dis[i] = 0;
} else dis[i] = -1;
}
while (q.size()) {
int u = q.front(); q.pop();
for (int v : adj[u]) {
if (rmatch[v] && dis[rmatch[v]] == -1) {
dis[rmatch[v]] = dis[u] + 1;
q.push(rmatch[v]);
}
}
}
}
bool dfs(int u) {
for (int v : adj[u]) {
if (!rmatch[v] || (dis[rmatch[v]] == dis[u] + 1 && dfs(rmatch[v]))) { // 注意这里括号
lmatch[u] = v; rmatch[v] = u;
return 1;
}
}
return 0;
}
int max_matching() {
int ans = 0;
while (1) {
bfs();
int d = 0;
for (int i = 1; i <= n; i++) {
if (!lmatch[i]) d += dfs(i);
}
if (!d) break;
ans += d;
}
return ans;
}
pair<vector<int>, vector<int>> minimum_vertex_cover() { // 最小点覆盖
vector<int> L, R;
for (int i = 1; i <= n; i++) {
if (dis[i] == -1) L.push_back(i);
else if (lmatch[i]) R.push_back(lmatch[i]);
}
return {L, R};
}
};
int n, m, M; // n,m: 左右点的数量,M:边的数量
int main() {
cin >> n >> m >> M;
HopcroftKarp hk(n, m);
while (M--) {
int u, v; cin >> u >> v;
hk.addEdge(u, v);
}
cout << hk.max_matching() << endl;
for (int i = 1; i <= n; i++) {
if (hk.lmatch[i]) cout << i << " " << hk.lmatch[i] << "\n";
}
}
例题
例1 洛谷P1963 NOI2009 变换序列
题意
给定一个序列 $0,1,…,N-1$,我们需要求出一个变换序列 $T$,其中 $T$ 是 $0$ 到 $N-1$ 的一个 permutation。
同时,我们定义任意两个数字 $i,j$ 之间的距离 $D(i,j) = \min \{ |i-j|, N-|i-j|\}$。
现在给定原序列 和 变换序列 $T$ 之间,每个元素的距离 $D_i$,求出一个字典序最小的变换序列 $T$,如果无解,则输出 “No Answer”。
其中,$N \leq 10^4$。
样例:
Input:
5
1 1 2 2 1
Output:
1 2 4 0 3
解释:原序列是 [0,1,2,3,4],距离序列是 [1,1,2,2,1],所以最终的变换序列可能是 [0+1, 1+1, 2+2, 3-|5-2|, 4-1] = [1,2,4,0,3]。
题解
将 原序列 作为二分图的左部分,变换序列作为二分图右部分。连边的方式就根据 距离序列 来。
例如原序列的第一个位置是 $0$,对应的距离序列第一个位置是 $1$,所以变换序列对应的值可能是 $1$ 或者 $4$。所以 $0 \rightarrow 1, 0 \rightarrow 4$ 连边即可。
连完边,跑一个最大匹配即可,如果最大匹配的数量等于 $N$ 说明有解,否则无解。
最后考虑一下 字典序最小 怎么解决?
一般来说,看到 字典序最小 就想到 贪心。所以第一个贪心思路是每次匹配的时候都 从小到大 找配对点。
然而这样有一个问题,比如 $0 \rightarrow 1$ 以后,有可能因为后续的匹配导致 $0 \rightarrow 4$。
所以我们按照编号大小,从后往前进行 DFS 即可。
for (int i = n; i >= 1; i--) { // 注意这里是从 n 到 1
id++;
dfs(i);
}
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
int match[maxn], vis[maxn], id = 0, d[maxn], n;
set<int> adj[maxn];
bool dfs(int i) {
for (int j : adj[i]) {
if (vis[j] == id) continue;
vis[j] = id;
if (!match[j]) {
match[j] = i;
return 1;
}
if (dfs(match[j])) {
match[j] = i;
return 1;
}
}
return 0;
}
bool ok(int i) { return i >= 1 && i <= n; }
int ans[maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> d[i];
for (int i = 1; i <= n; i++) {
int j = (i - d[i]);
if (ok(j)) adj[i].insert(j);
j = (i + d[i]);
if (ok(j)) adj[i].insert(j);
j = (i + (n - d[i]));
if (ok(j)) adj[i].insert(j);
j = (i - (n - d[i]));
if (ok(j)) adj[i].insert(j);
}
for (int i = n; i >= 1; i--) {
id++;
dfs(i);
}
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (match[i]) cnt++;
}
if (cnt < n) {
cout << "No Answer" << "\n";
} else {
for (int i = 1; i <= n; i++) ans[match[i]] = i;
for (int i = 1; i <= n; i++) cout << ans[i]-1 << " ";
cout << endl;
}
}
例2 洛谷 P2825 [HEOI2016/TJOI2016]游戏
题意
在游戏 “泡泡堂” 中,给定一个 $n \times m$ 的网格,其中 * 代表空地,x 代表软石头,# 代表硬石头。
每个炸弹会影响它所在的行与列。炸弹可以穿透软石头,但是无法穿透硬石头。
给定一个地图,求最多放置多少个炸弹,使得每两个炸弹之间不会互相炸到?
题解
二分图匹配的一个常见套路就是应用在 网格地图 中。
我们把 每一行 看作一个节点,每一列 也看作一个节点,而每个网格就看作一条边。
如果我们不考虑硬石头的情况,那么这个题非常简单。把每个空地看作一条边,连起来以后跑一个最大匹配即可。
但是现在有硬石头。我们会发现一个硬石头可以 隔断纵向的和横向的 炸弹威力。那么,我们把硬石头隔断的部分,也看作是一个节点即可。
也就是说,现在不再是每一行/每一列作为节点,而是以 横向/纵向 线段 作为单位,每个线段是一个节点。
现在,每个网格里有 $3$ 种情况:
- 空地:看作一个正常的边
- 软石头:忽略不计
- 硬石头:作为分界点,上下是两个不同的线段,左右是两个不同的线段。
图建好了,再跑一个最大匹配即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 55;
const int maxm = 2505;
int n,m;
char arr[maxn][maxn];
vector<int> adj[maxm];
int id, lcnt, rcnt;
int l[maxn][maxn], r[maxn][maxn];
int match[maxm], vis[maxm], vis_id;
bool dfs(int i) {
for (int j : adj[i]) {
if (vis[j] == vis_id) continue;
vis[j] = vis_id;
if (!match[j] || dfs(match[j])) {
match[j] = i;
return 1;
}
}
return 0;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> arr[i][j];
}
}
id = 0;
for (int i = 1; i <= n; i++) {
id++;
for (int j = 1; j <= m; j++) {
if (arr[i][j] == '#') {
id++;
continue;
}
l[i][j] = id;
}
}
lcnt = id;
id = 0;
for (int j = 1; j <= m; j++) {
id++;
for (int i = 1; i <= n; i++) {
if (arr[i][j] == '#') {
id++;
continue;
}
r[i][j] = id;
}
}
rcnt = id;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (arr[i][j] == '*') {
adj[l[i][j]].push_back(r[i][j]);
}
}
}
int ans = 0;
for (int i = 1; i <= lcnt; i++) {
vis_id++;
ans += dfs(i);
}
cout << ans << endl;
}
