网络流
Contents
介绍
网络 是一个有向图 $G = (V,E)$,每条边 $(u,v) \in E$ 都拥有一个容量 $c(u,v)$。
在一个网络中,拥有两个特殊的节点 $s, t$ (源点,汇点)。
定义 流 为一个函数 $f(u,v)$,其中 $u,v \in V$,满足:
- 容量限制:每条边的流不能超过这条边的容量,即 $f(u,v) \leq c(u,v)$。
- 斜对称性:每条边的流量,与其相反边的流量,互为相反数,即 $f(u,v) = -f(v,u)$。
- 流守恒性:从源点 $s$ 流出的流量,等于汇点 $v$ 流入的流量。同时对于每个点 $u$(除了 $s,t$),流入 $u$ 的流量需要等于 流出 $u$ 的流量。
定义 残量网络 为:对于一个流函数 $f$,残量网络 $G_f$ 是网络 $G$ 中 所有的节点 和 剩余容量 $> 0$ 的边 组成的子图。
残量网络中,可能存在 原图中不存在的边(一条边剩余流量,产生的反向边,也能算入残量网络)。
网络流的三种问题类型:最大流,最小割,费用流。
最大流
定义一个网络的流量为:汇入 $t$ 的流量之和。
最大流就是求:从 $s$ 流到 $t$ 的最大流量。
最小割
如果我们要从原图中,切掉一个 边集 $E’ \subseteq E$,使得 $s,t$ 无法联通。
让这个边集的容量和 最小,就是最小割。
• 在数值上,最小割 等于 最大流,如果要求出具体是哪些边,可以看残量网络。
费用流
每一条边 $(u,v)$ 都有一个费用 $w(u,v)$,每当有 $1$ 个单位的流量流过这条边,就要付出 $w(u,v)$ 的代价。
在 保证最大流 的基础上,求出 最小/最大费用,就是 费用流。
算法
定义 增广路 为:残量网络中,一条从 $s$ 到 $t$ 的路径。
如果我们要求最大流,那么 当前的流是最大流 $\iff$ 残量网络 $G_f$ 中不存在增广路(即,残量网络中 $s,t$ 不相连)。
EK算法
$EK$ 算法的思想就是:每一轮增广,都用 BFS 在 残量网络 上找到一个增广路,然后根据这个路径上,最小 的剩余流量,来流过这条路径。然后更新残量网络,直到残量网络中不存在增广路。
由于实践中一般不用,所以就不多赘述。
Dinic算法
思想与 EK 算法相同,在每一轮增广时,按照以下顺序进行操作:
- 从源点 $s$ 开始进行 BFS,获得一张分层图。
- 利用 DFS 进行增广,增广过程中保证一定是从 第 $x$ 层增广到 第 $(x+1)$ 层。利用 DFS 增广的好处是可以多路增广,在一条路径增广完毕,回溯的时候可以寻找下一条。
Dinic 算法有几个重要的优化:
- 删点:在一个点 $u$ 尝试向外流的时候,如果成功流出的流量为 $0$,说明这个点 $u$ 已经无法向 $t$ 推送流量了,我们将这个点的
dis[u] = -1。意思为删除这个点。 - 当前弧优化:在 DFS 过程中,如果我们推完了一条边,然后回溯了,这说明,要么 走这条边已经无法连通到 $t$了,要么 入流量用完了。无论是哪一种,都说明我们无法再使用这条边了。所以就在本轮增广中,删去这条边。在代码中,使用
cur[]数组来实现。
复杂度:$O(n^2m)$,在实际使用中,一般跑的比这个快(所以不用太担心复杂度问题)。
费用流
在 Dinic 的基础上,把 BFS求分层图 的过程,改成 SPFA求最短路 即可。然后在增广的过程中,只走最短路径。
同时,如果有费用为 $0$ 的边,使得这条边,及其反向边的费用均为 $0$,这可能会导致算法的最短路一直在这两个节点之间走。为了防止这个问题导致死循环,我们需要一个 vis[] 数组保证在 DFS 过程中每个点只被访问一次。
复杂度:$O(n^2m^2)$,在实际使用中,一般跑的比这个快(所以不用太担心复杂度问题)。
• 特别的,对于单位容量的网络,复杂度为 $O(m * \min(\sqrt m, n^{\frac{2}{3}}))$。
• 对于二分图匹配问题,复杂度为 $O(m\sqrt n)$。
模版
最大流模版
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
ll maxflow() {
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
return ans;
}
int main() {
cin >> n >> m >> s >> t;
for (int i = 1; i <= m; i++) {
int u,v; ll w;
cin >> u >> v >> w;
add(u, v, w);
}
cout << maxflow() << endl;
}
费用流模版
struct Edge {
int to, nxt;
ll w, c;
};
struct MCMF {
int n,m,s,t;
Edge edges[maxm<<1];
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
ll cost = 0;
void addEdge(int u, int v, ll w, ll c) {
Edge e = {v, head[u], w, c};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dis[maxn];
bool inq[maxn], vis[maxn];
bool spfa(bool mincost) {
queue<int> q;
memset(vis, 0, sizeof(vis)); // 这里一定要记得清空 vis (dfs要用)
memset(inq, 0, sizeof(inq));
fill(dis, dis+maxn, mincost ? 1e18 : -1e18);
memcpy(cur, head, sizeof(head)); // 当前弧优化用到的数组 cur
dis[s] = 0;
inq[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (w == 0) continue;
if ((mincost && dis[u] + c < dis[to]) || (!mincost && dis[u] + c > dis[to])) {
dis[to] = dis[u] + c;
if (!inq[to]) {
inq[to] = 1;
q.push(to);
}
}
}
}
return dis[t] != (mincost ? 1e18 : -1e18);
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
vis[u] = 1;
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (vis[to] || w == 0 || dis[to] != dis[u] + c) continue;
// 检测: 1. 是否vis过 2. 这条边是否存在 3. 是否是最短路径
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break;
}
if (out == 0) dis[u] = -1e18;
return out;
}
ll mcmf(bool mincost = true) {
ll maxflow = 0;
while (spfa(mincost)) {
ll res = dfs(s, 1e18);
maxflow += res;
cost += res * dis[t]; // cost += (流量 * 最短路长度)
}
return maxflow;
}
void add(int u, int v, ll w, ll c) {
addEdge(u,v,w,c);
addEdge(v,u,0,-c);
}
void clear() {
ecnt = 2;
memset(head, 0, sizeof(head));
memset(cur, 0, sizeof(cur));
memset(edges, 0, sizeof(edges));
cost = 0;
}
} flow;
int main() {
cin >> n >> m >> s >> t;
for (int i = 1; i <= m; i++) {
int u,v,w,c;
cin >> u >> v >> w >> c;
flow.add(u,v,w,c);
}
ll maxflow = flow.mcmf(true); // 最小费用流,返回最大流
cout << maxflow << " " << flow.cost << endl;
}
性质
最小割的可行边和必要边
最小割是一个 set of edges,使得割掉这些 edges 将原图一分为二,并且这些 edges 的容量之和最小。
如何判断哪些边是 必要边(指这条边存在于 所有最小割 中),哪些是可行边(指这条边存在于 至少一个最小割 中)?
可行边:
一条边 $(u,v)$ 是可行边当且仅当:
- 必须满流
- 在残量网络中,$u$ 不存在到达 $v$ 的路径。(等价于 $3$)
- 在残量网络中,$u,v$ 不在同一个强连通分量中。
证明:
- 根据最小割和最大流的关系,一个边存在于一个最小割中 $\iff$ 这个边满流。
- 如果存在 $u$ 到 $v$ 的路径,那么由于残量网络中一定有 $(v,u)$ 这条边(反向边),所以可以退流,通过 $u \rightarrow v$ 的另外一条路径来走,所以 $(u,v)$ 在一个新的最大流方案中就不再满流了,于是不可能是可行边。
- 由 $2$,由于 $(v,u)$ 一定存在,所以存在 $u \rightarrow v$ 的路径 $\iff$ $u,v$ 在同一个强联通分量中。
必要边:
一条边 $(u,v)$ 是可行边当且仅当:
- 必须满流
- 在残量网络中,存在 $s \rightarrow u$ 的路径,和 $v \rightarrow t$ 的路径。(等价于 $3$)
- 在残量网络中,$s,u$ 在同一个强联通分量中,且 $v,t$ 在同一个强联通分量中。
证明:
-
同上
-
考虑最小割的构造方案:我们先跑一发最大流,此时残量网络中不存在 $s \rightarrow t$ 的路径,然后从 $s$ 开始跑一次 bfs,所有能被 $s$ 访问到的点作为集合 $S$,而剩下的作为集合 $T$,$S \rightarrow T$ 的边就是最小割了。
所以如果存在 $s \rightarrow u$ 的路径,和 $v \rightarrow t$ 的路径,那么这条边一定是 $S \rightarrow T$ 的边,意味着如果删掉它,那么最大流的值就会减小,这也意味着它是一个必要边。
-
由于是残量网络,在跑最大流的过程中,一定跑了一条增广路 $s \rightarrow u \rightarrow v \rightarrow t$,这意味着在残量网络中一定有一条 $u \rightarrow s$ 的路径,同理有一条 $t \rightarrow v$ 的路径。
所以 $s,u$ 在同一个强联通分量中,且 $v,t$ 在同一个强联通分量中 $\iff$ 存在 $s \rightarrow u$ 的路径,和 $v \rightarrow t$ 的路径。
所以判断可行边和必要边,只要在残量网络上跑一个tarjan处理scc即可。
• 这也意味着,判断一个最大流/最小割是否是unique的,只要在残量网络上,从 $s$ 出发,然后从 $t$ 出发,看所有的点是否都被访问过即可(这也等价于所有可行边都是必要边)。
最小割边数的最小割
要在基于最小割的基础上,求出最小割边数。
于是我们可以先跑一个最大流,跑出所有可能的满流边,问题就转变成 最少割掉多少个满流边,使得 $s$ 无法到达 $t$?
所以本质上相当于只考虑满流边,容量赋为1,重新跑一次最小割。
• 实际代码:对于所有未满流边,容量赋为 inf,所有满流边,正向边容量 $+1$,所有反向边都不用动,然后再跑一次最大流即可。
代码
int main() {
int T; cin >> T;
while (T--) {
cin >> n >> m >> s >> t;
for (int i = 1; i <= m; i++) {
int u,v; ll w;
cin >> u >> v >> w;
add(u, v, w);
}
maxflow();
for (int e = 2; e < ecnt; e += 2) {
if (edges[e].w == 0) {
edges[e].w++;
} else {
edges[e].w = 1e9;
}
}
cout << maxflow() << "\n";
clearall();
}
}
套路
二元决策(最小割模型)
有一类问题:有 $n$ 个元素,每个元素要么放入集合 $A$,要么放入集合 $B$,放入集合 $A,B$ 会产生不同的收益,同时可能还会有 相邻 的元素 / 特定的一些元素组合 在同一个集合/不同集合中,就产生额外的收益。求最大/最小的收益。
一般套路为:对于每个元素 $u$,连 $(s,u), (u,t)$ 的边。
例如我们用 $s$ 表示集合 $A$,用 $t$ 表示 $B$。哪条边 被保留下来了,就代表选择了这个元素 $u$ 被放入了哪个集合。
在最小割中,要么 $(s,u)$ 被割掉,要么 $(u,t)$ 被割掉,这说明每个元素最终只会被放入其中的一个集合。
对于 特定元素组合 产生的额外收益,举个例子:
比如 $u,v$ 都放入集合 $A$ (与 $s$ 相连) 就会产生额外收益 $k$ 的话。就创造一个额外的节点 $x$,连接有向边 $(x,u), (x,v), (s,x)$,其中令 $(x,u), (x,v)$ 的流量为 $inf$,而令 $(s,x)$ 的流量为 $k$。
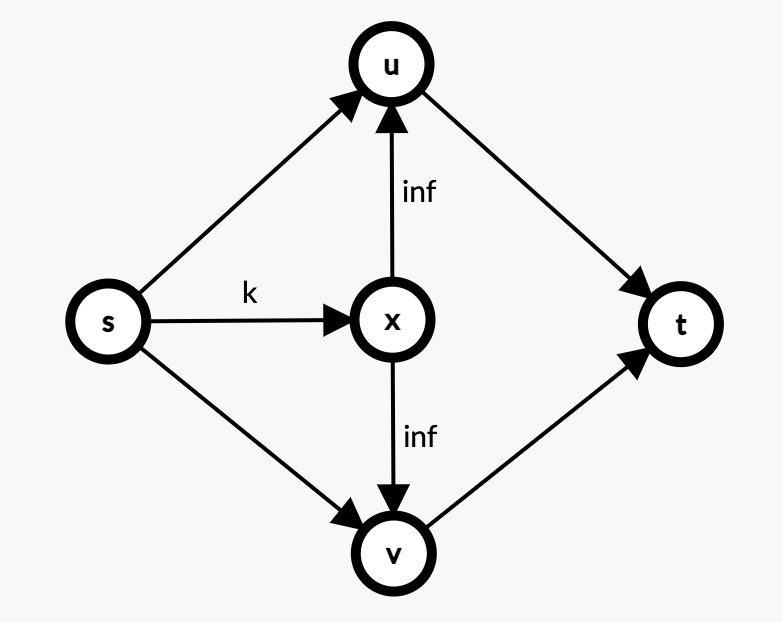
解释:流量为 $inf$ 的边代表在最小割中一定不会被割去,而如果 $u,v$ 之间,有任何一个元素 没有被放入集合 $A$,那么它就一定会与 $t$ 相连,此时,为了保证图不联通,在最小割中,就一定会割掉 $(s,x)$ 这条边,所以就损失了 $k$ 的收益。
区间覆盖模型(不等式模型)
给定多种区间,每种区间可以使用一定次数,每次使用有一个代价 cost,在一条直线上,有一些点我们需要覆盖多次。求最小的 cost 使得这些覆盖条件被满足?
我们以直线上,每个点作为一个节点。
对于一个区间 $[a,b]$,使用次数限制为 $w$,代价为 $c$。
则:由 $a$ 对应的节点 $u$,连一条边到 $b$ 对应的节点 $v$,容量为 $w$(代表这个区间可以被选择 $w$ 次),代价为 $c$。
怎么满足/限制 直线上每个点,被覆盖的次数呢?
直觉上说,由每个节点连边到 $t$。但是这样不对,因为这里的区间是 强制覆盖 $[a,b]$,并不能覆盖一半的。
正确的方法是:将所有的点,连边连成一条直线。相当于,原本直线上每个点对应一个节点,现在我们把这些节点按照它们原来的方式连边。
如果第 $i$ 个点,需要被覆盖 $a_i$ 次,那么就连一条边 $(i,i+1,-a_i,0)$(流量为负数,实现中,可以使用 $inf - a_i$ 来代替),代表这里少了 $a_i$ 个点。
如何保证这些点一定被覆盖了呢?用最大流来限制即可。
由 $s$ 向 $1$ 连接容量为 $inf$ 的边,cost 为 0;由 $n$ 向 $t$ 连接容量为 $inf$ 的边,cost 为 0。
费用流保证最大流的过程中,就会保证每个点被覆盖了相应的次数。
网络流例题
例1 洛谷P4016 负载平衡问题
题意
有 $n$ 个环形排列的仓库,给定每个仓库初始的储存量 $a_i$。
我们只能在相邻的仓库之间搬运。
求最少的搬运量,使得 $n$ 个仓库的库存数量相同。(保证储存量的平均数是一个整数)。
其中,$1 \leq n \leq 100$。
题解(贪心)
正解实际上是 $O(n\log n)$ 的贪心,一个标准的均分纸牌问题。(加强版的在这:洛谷P2512 HAOI2008 糖果传递)。
设第 $i$ 个人 向右传递 了 $x_i$。注意到这里 $x_i$ 可正可负可零。
则目标是求 $\min \{ |x_1| + |x_2| + … + |x_n|\}$。
因为最后每个人都获得了 $a$($a$ 就是平均数)。
则有:$a_1 + x_1 - x_2 = a, a_2 + x_2 - x_3 = a$,以此类推。
进行代换,可得:
$$x_2 = x_1 - (a-a_1)$$ $$x_3 = x_1 - (2a-a_1-a_2)$$ $$x_4 = x_1 - (3a-a_1-a_2-a_3)$$ $$…$$ $$x_n = x_1 - ((n-1)a - a_1 - a_2 - … - a_{n-1})$$
所以就只剩下一个变量 $x_1$ 了。
因为 $x_1$ 的值可以随便选,由上面的表达式可以看出,这相当于在一个直线上,有 $n$ 个点,坐标为:
$$0,(a-a_1 ),(2a-a_1-a_2 ),(3a-a_1-a_2-a_3 ),…,((n-1)a-a_1-a_2-…-a_{n-1} )$$
选择直线上一个点,使得它到这 $n$ 个点距离之和最短?很明显,选这些点的中位数即可。
题解(网络流)
需要最小化搬运数量。很明显是一个费用流。
网络流的常见套路 $1$:创建超级源点 $s$ 和 超级汇点 $t$。
对于相邻的节点,我们链接一个双向的边,费用为 $1$,容量无限。
同时创建超级源点 $s$,超级汇点 $t$,使得:
$s$ 向每个节点 $i$ 连接一个 费用为 $0$,容量等于 $a_i$ 的边。
每个节点 $i$ 向汇点 $t$ 连接一个 费用为 $0$,容量等于 $avg$(储存量的平均数)的边。
答案就是最小费用。
网络流代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int maxm = 5e4+5;
int n, s, t, mincost = 0;
int arr[maxn];
struct Edge {
int to, nxt, w, c;
} edges[maxn<<4];
int head[maxn], ecnt = 2, cur[maxn];
void addEdge(int u, int v, int w, int c) {
Edge e = {v, head[u], w, c};
edges[ecnt] = e;
head[u] = ecnt++;
}
bool inq[maxn];
int dis[maxn];
bool spfa() {
fill(dis, dis+maxn, 1e9);
memset(inq, 0, sizeof(inq));
memcpy(cur, head, sizeof(head));
queue<int> q;
q.push(s);
dis[s] = 0;
inq[s] = 1;
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to, w = edges[e].w, c = edges[e].c;
if (w == 0) continue;
if (dis[u] + c < dis[to]) {
dis[to] = dis[u] + c;
if (!inq[to]) {
inq[to] = 1;
q.push(to);
}
}
}
}
return dis[t] != 1e9;
}
bool vis[maxn];
int dfs(int u, int in) {
if (u == t) return in;
vis[u] = 1;
int out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to, w = edges[e].w, c = edges[e].c;
if (w == 0 || vis[to] || dis[u] + c != dis[to]) continue;
int res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break;
}
if (out == 0) dis[u] = -1e9;
return out;
}
int mcmf() {
int maxflow = 0;
while (spfa()) {
memset(vis, 0, sizeof(vis)); // 这里一定要记得清空 vis
int res = dfs(s, 1e9);
maxflow += res;
mincost += res * dis[t]; // cost += (流量 * 最短路长度)
}
return maxflow;
}
int main() {
fastio;
cin >> n;
int sum = 0;
for (int i = 1; i <= n; i++) cin >> arr[i], sum += arr[i];
sum /= n;
s = n+1, t = n+2;
for (int i = 1; i <= n; i++) {
addEdge(s, i, arr[i], 0);
addEdge(i, s, 0, 0);
addEdge(i, t, sum, 0);
addEdge(t, i, 0, 0);
if (i != n) {
addEdge(i, i+1, 1e9, 1);
addEdge(i+1, i, 0, -1);
addEdge(i+1, i, 1e9, 1);
addEdge(i, i+1, 0, -1);
}
}
addEdge(n, 1, 1e9, 1);
addEdge(1, n, 0, -1);
addEdge(1, n, 1e9, 1);
addEdge(n, 1, 0, -1);
mcmf();
cout << mincost << endl;
}
例2 洛谷P2774 方格取数问题
题意
给定一个 $n \times m$ 的方格图,每个方格中有一个正整数。
要从方格中取数,使任意两个数所在方格没有公共边,求取出的数的最大和。
其中,$n,m \leq 100$。
题解
首先这题的限制条件是 不能相邻。对于一个方格来说,只有相邻的(最多4个)方格不能被选。
所以我们应该从 禁止选择 的角度考虑这个问题,也就是说,应该先选择所有的方格,然后删掉那些互斥的部分。
如果进行建图:每个方格都是一个 点,然后按照互斥条件进行 连边。
可以发现,如果我们把这个方格图进行 二分图染色,一定有一个合理的方案。保证相邻的方格颜色不同即可。
如果对方格图进行染色,建图后,就可以得到一张 二分图。
二分图有什么用呢?
我们最终的目标是使得 整张图中不存在互斥情况,并且 使得删掉的那些方格权值和最小。
那么我们建立超级源点 $s$,汇点 $t$,然后将 $s$ 连向所有的左侧点(容量为对应点的权值),所有的右侧点连向 $t$(容量为对应点的权值),我们可以发现:
- $s \rightarrow u$ 代表节点 $u$ 被选择了。
- $v \rightarrow t$ 代表节点 $v$ 被选择了。
- 如果整张图是 连通的,说明仍然存在互斥情况。
所以我们要 使得删掉的那些方格权值和最小,只要保证删掉的边的权值和最小,使得整张图不连通即可。
求这张图的 最小割 即可。答案就是 所有权值的和 减去 最小割。
总结一下这题:
- 互斥的点 的颜色一定不同,使得我们可以转化为 二分图模型。
- 互斥的点之间连边,代表了互斥关系。
- 图的连通性代表了是否消除了所有的互斥条件。
参考链接:https://www.luogu.com.cn/problem/solution/P2774
另外一道几乎一样的例题是 骑士共存问题。
题意大概是在一个 $n \times n$ 的棋盘上,有些格子不能放,问最多能放几个马,使得它们互相不会攻击。
我们会发现按照 横坐标 $x$ 和 纵坐标 $y$ 之和 $(x+y)$ 的奇偶性进行染色分类,仍然是个二分图,剩下的就和本题一样了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int maxm = 4e4+5;
int vid[102][102], color[maxn];
ll val[102][102];
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
int delta[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int main() {
cin >> n >> m;
int id = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> val[i][j];
vid[i][j] = ++id;
if ((i+j) & 1) color[id] = 1;
else color[id] = 0;
}
}
s = n*m+1, t = n*m+2;
ll ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int ID = vid[i][j];
ans += val[i][j];
if (color[ID] == 1) {
add(s, ID, val[i][j]);
for (int d = 0; d < 4; d++) {
int di = delta[d][0] + i, dj = delta[d][1] + j;
if (di >= 1 && di <= n && dj >= 1 && dj <= m) {
add(ID, vid[di][dj], 1e18);
}
}
} else {
add(ID, t, val[i][j]);
}
}
}
while (bfs()) {
ans -= dfs(s, 1e18);
}
cout << ans << endl;
}
例3 洛谷P1251 餐巾计划问题
题意
总共有 $N$ 天,第 $i$ 天需要 $r_i$ 个干净的餐巾。每天结束时,餐厅需要决定如何处理脏餐巾,有以下几个选项:
- 不处理,留到之后再洗。
- 送去快洗部,洗一块需要 $m$ 天,费用为 $f$ 元。
- 送去慢洗部,洗一块需要 $n$ 天,费用为 $s$ 元。
同样,餐厅在每天开始/结束时,可以选择购买新的餐巾,每块新餐巾的费用为 $p$ 元。
求出最少花费,使得每天需要的餐巾数满足要求,初始情况下,餐巾数为 $0$。
其中,$N \leq 2000$。
题解
网络流的常见套路 $2$:拆点
一个比较明显的费用流思路:
将每一天看作一个节点,然后每个节点拆成 $2$ 个,分别表示 干净餐巾 和 脏餐巾。
换个角度来看,就是将每个节点拆成了 每天的开始(需要提供干净餐巾) 和 每天的结束(产出了一些脏餐巾)。
我们设:第 $i$ 天的节点分别为 $s_i, e_i$ (对应干净,脏)。
那么对于脏餐巾的处理,我们可以这样连边:
- 不处理,留到之后再洗:从 $t_i$ 连边到 $t_{i+1}$,费用为 $0$,容量为 $\inf$。
- 送到快洗部(洗一块需要 $m$ 天,费用为 $f$ 元):从 $t_i$ 连边到 $s_{i+m}$,费用为 $f$,容量为 $\inf$。
- 送去慢洗部(洗一块需要 $n$ 天,费用为 $s$ 元):从 $t_i$ 连边到 $s_{i+n}$,费用为 $s$,容量为 $\inf$。
剩下的问题是:购买新餐巾,每天需要提供 $r_i$ 个干净餐巾,每天需要让 $r_i$ 个干净餐巾变成脏的。
- 购买新餐巾(一条 $P$ 元):源点 $s$ 向每个 $i$ 对应的 $s_i$ 连一条边,费用为 $P$,容量为 $\inf$。
- 每天需要提供 $r_i$ 个干净餐巾:从每个 $i$ 对应的 $s_i$ 向汇点 $t$ 连一条边,费用为 $0$,容量为 $r_i$。
- 每天需要让 $r_i$ 个干净餐巾变成脏的:源点 $s$ 向每个 $i$ 对应的 $t_i$ 连一条边,费用为 $0$,容量为 $r_i$。
• 这里重点讲一下 $5,6$:我们如何强制保证干净餐巾够用呢?
注意到我们求的是最小费用 最大流。所以通过 限制流量 来保证干净餐巾的数量,也就是让每天的干净节点 $s_i$ 都流向汇点 $t$。
但是如果干净餐巾流向了 $t$,就必须保证从 $s$ 开始有脏餐巾流向 $t_i$,才能保证流量守恒(不买餐巾的情况下,餐巾的总数守恒)。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4005;
const int maxm = 5e4+5;
int n,s,t,arr[maxn];
struct Edge {
int to, nxt;
ll w, c;
} edges[maxn<<4];
int head[maxn], ecnt = 2, cur[maxn];
void addEdge(int u, int v, ll w, ll c) {
Edge e = {v, head[u], w, c};
edges[ecnt] = e;
head[u] = ecnt++;
}
queue<int> q;
ll dis[maxn];
bool inq[maxn];
bool spfa() {
memset(inq, 0, sizeof(inq));
fill(dis, dis+maxn, 1e18);
memcpy(cur, head, sizeof(head));
dis[s] = 0;
inq[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (w == 0) continue;
if (dis[u] + c < dis[to]) {
dis[to] = dis[u] + c;
if (!inq[to]) {
inq[to] = 1;
q.push(to);
}
}
}
}
return dis[t] != 1e18;
}
bool vis[maxn];
ll dfs(int u, ll in) {
if (u == t) return in;
vis[u] = 1;
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (w == 0 || vis[to] || dis[to] != dis[u] + c) continue;
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break;
}
if (out == 0) dis[u] = -1e18;
return out;
}
ll mincost = 0;
ll mcmf() {
ll maxflow = 0;
while (spfa()) {
memset(vis, 0, sizeof(vis));
ll res = dfs(s, 1e18);
maxflow += res;
mincost += res * dis[t];
}
return maxflow;
}
void add(int u, int v, ll w, ll c) {
addEdge(u,v,w,c);
addEdge(v,u,0,-c);
}
int main() {
fastio;
cin >> n;
ll sum = 0;
for (int i = 1; i <= n; i++) cin >> arr[i], sum += arr[i];
ll P,M,F,N,S;
cin >> P >> M >> F >> N >> S;
s = 2*n + 1, t = 2*n+2;
for (int i = 1; i <= n; i++) {
add(s, i, 1e18, P);
add(i, t, arr[i], 0);
add(s, i+n, arr[i], 0);
if (i != n) {
add(i+n, i+n+1, 1e18, 0);
}
if (i + M <= n) {
add(i+n, i+M, 1e18, F);
}
if (i + N <= n) {
add(i+n, i+N, 1e18, S);
}
}
ll ans = mcmf();
assert(ans == sum);
cout << mincost << endl;
}
例4 洛谷P2764 最小路径覆盖问题
题意
给定一个 DAG(有向无环图),$n$ 个节点,$m$ 条边。
定义一个路径覆盖为:由多个简单路径组成,覆盖了所有节点,并且每个节点被覆盖了仅一次,一条路径最短可以仅为一个节点。
求这个 DAG 的最小路径覆盖(路径数量最小)。
其中,$1 \leq n \leq 150, 1 \leq m \leq 6000$。
题解
我们考虑一下怎么让 路径数量 最小?
初始状态下,令每一个节点本身都是一条路径,那么我们可以让路径合并,合并的方式就是 一个路径的尾部 和 另外一个路径的头部 连在一起。最后的总路径条数就等于 $n$ 减去合并的次数。
而每个节点可以作为一个路径的头部,也可以作为一个路径的尾部,且每个节点在路径合并的过程中,最多只能成为一次头部/尾部。
那我们就进行 拆点。
将每个节点 $u$ 拆成 $2$ 种,一种是 尾部 $u_1$,一种是 头部 $u_2$。如果 $u \rightarrow v$ 在 DAG 中是一条边,那么就在新图中,连一条 $u_1 \rightarrow v_2$ 的边。
可以发现,这个新图是一个二分图,其最大匹配就是合并路径的次数。
所以答案就是 $n$ 减去最大匹配。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 155;
const int maxm = 6e4+5;
int n,m,head[maxn<<1], ecnt = 1, match[maxn<<1], vis[maxn<<1], visid = 0;
struct Edge {
int to, nxt;
} edges[maxm<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
bool dfs(int u) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (vis[to] == visid) continue;
vis[to] = visid;
if (!match[to] || dfs(match[to])) {
match[to] = u;
return 1;
}
}
return 0;
}
int from[maxn];
int main() {
fastio;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u,v; cin >> u >> v;
addEdge(u, v+n);
}
int ans = n;
for (int i = 1; i <= n; i++) {
visid++;
ans -= dfs(i);
}
// 处理答案
for (int i = n+1; i <= 2*n; i++) {
if (match[i])
from[match[i]] = i-n;
}
for (int i = n+1; i <= 2*n; i++) {
if (!match[i]) {
int j = i-n;
while (j) {
cout << j << " ";
j = from[j];
}
cout << "\n";
}
}
cout << ans << endl;
}
可相交最小路径覆盖
注意到,上面说的是不相交的最小路径覆盖。
对于可相交的最小路径覆盖,我们可以考虑重新建一张图,如果对于所有的 $u,v$,$u$ 能够到达 $v$,那么在新图中建 $u \rightarrow v$ 这条边。
然后在新图跑一个最小路径覆盖即可。
• 对于每一个 $u$ 都跑一个 bfs 就可以得到它能够到达的所有 $v$ 了。
例5 洛谷P2766 最长不下降子序列问题
题意
给定一个正整数序列 $x_1, x_2, …, x_n$。
- 计算最长不下降子序列(不需要连续)的长度 $s$。
- 如果每个元素只允许使用一次,计算从给定的序列中最多可取出多少个长度为 $s$ 的不下降子序列。
- 如果允许在取出的序列中多次使用 $x_1, x_n$,(其他元素仍然只允许使用一次),则从给定序列中最多可取出多少个 不同的 长度为 $s$ 的不下降子序列。
其中,$1 \leq n \leq 500$。
题解
第一个问题是标准的 $O(n^2)$ DP。
第二问和第三问要用到网络流。
我们如何得到一个合法的子序列?这里利用到了 分层图 思想。
我们先求出,对于每一个 index $i$,以index $i$ 结尾的最长不下降子序列的长度,设其为 $f_i$。
那么如果一个子序列合法,子序列中的每个元素 $f_{i_1}$,和它下一个元素 $f_{i_2}$ 的关系一定是 $f_{i_1} + 1 = f_{i_2}$。
所以我们按照 $f_i$ 的值进行分层,只有 $f_i = x$ 的节点可以连向 $f_j = x+1$ 的节点。
我们要求最长的子序列,那么就让源点 $s$ 连边到 $u$($f_u = 1$)。让 $v$ 连边到 $t$($f_v = s$)。求一个最大流就是答案了。
现在考虑第二问:每个元素只允许使用一次。我们发现之前的建图就已经足够了,跑最大流即可。
第三问:$x_1, x_n$ 允许使用多次。我们可以通过控制 流量 来控制这个变量。
如何控制一个节点的入流量和出流量?拆点!
将每个节点 $u$ 拆成两个节点,分别代表入点 $u_{in}$ 和 出点 $u_{out}$。
所有原先 进入 $u$ 的边,现在都改为 进入 $u_{in}$,
所有原先 离开 $u$ 的边,现在都改为 离开 $u_{out}$。
连一条边 $u_{in} \rightarrow u_{out}$。这一条边的流量,就代表了这个节点 $u$ 被限制的入流量和出流量。
综上,第二问和第三问的模型都可以拆点,只不过第二问对于每一个节点 $u$,限制的流量均为 $1$。
而第三问中,对于节点 $1,n$,不限制流量(即 $in, out$ 中间这条边的流量为 $\inf$)。
参考链接:https://oi-wiki.org/graph/node/
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
const int maxm = 2e5+5;
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
int arr[maxn], dp[maxn], len = 0;
void solve1() {
if (len == 1) {
cout << n << endl;
return;
}
// subtask 1
for (int i = 1; i <= n; i++) {
if (dp[i] == 1) add(s, i, 1e18);
add(i, i+n, 1);
if (dp[i] == len) add(i+n, t, 1e18);
for (int j = i+1; j <= n; j++) {
if (dp[j] == dp[i] + 1) add(i+n, j, 1);
}
}
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
cout << ans << endl;
}
void solve2() {
// subtask 2
if (len == 1) {
cout << n << endl;
return;
}
ecnt = 2;
memset(head, 0, sizeof(head));
for (int i = 1; i <= n; i++) {
if (dp[i] == 1) add(s, i, 1e18);
if (i == 1 || i == n)
add(i, i+n, 1e18);
else
add(i, i+n, 1);
if (dp[i] == len) add(i+n, t, 1e18);
for (int j = i+1; j <= n; j++) {
if (arr[j] >= arr[i] && dp[j] == dp[i] + 1) add(i+n, j, 1);
}
}
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
cout << ans << endl;
}
void build() {
for (int i = 1; i <= n; i++) {
dp[i] = 1;
for (int j = i-1; j >= 1; j--) {
if (arr[j] <= arr[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
len = max(len, dp[i]);
}
cout << len << endl;
s = 2*n+1, t = 2*n+2;
solve1();
solve2();
}
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) cin >> arr[i];
build();
}
例6 洛谷P1646 Happiness
题意
给定一个 $n \times m$ 的座位表,每个同学要选择理科或者文科,每个人选择理科时,会获得喜悦值 $a_{ij}$,选择文科时会获得喜悦值 $b_{ij}$。
位于 $(i,j)$ 的同学,如果和 $(i+1, j)$ 的同学同时选择了理科,会获得额外 $c_{ij}$ 的喜悦值,如果同时选择文科,会获得 $d_{ij}$ 的喜悦值。
位于 $(i,j)$ 的同学,如果和 $(i, j+1)$ 的同学同时选择了理科,会获得额外 $e_{ij}$ 的喜悦值,如果同时选择文科,会获得 $f_{ij}$ 的喜悦值。
求喜悦值的最大和。
其中,$n,m \leq 100$。
题解
最小割的二元选择模型。
首先每个同学是一个节点 $u$,然后连接 $(s,u,a), (u,t,b)$。
然后对于两个相邻的同学,创造一个新的节点 $x$,连接 $(s,x,c), (x,u,inf), (x,v,inf)$。(其中 $c$ 代表同时选择文科的额外喜悦值),再创造一个节点 $y$,连接 $(y,t,d), (u,y,inf), (v,y,inf)$
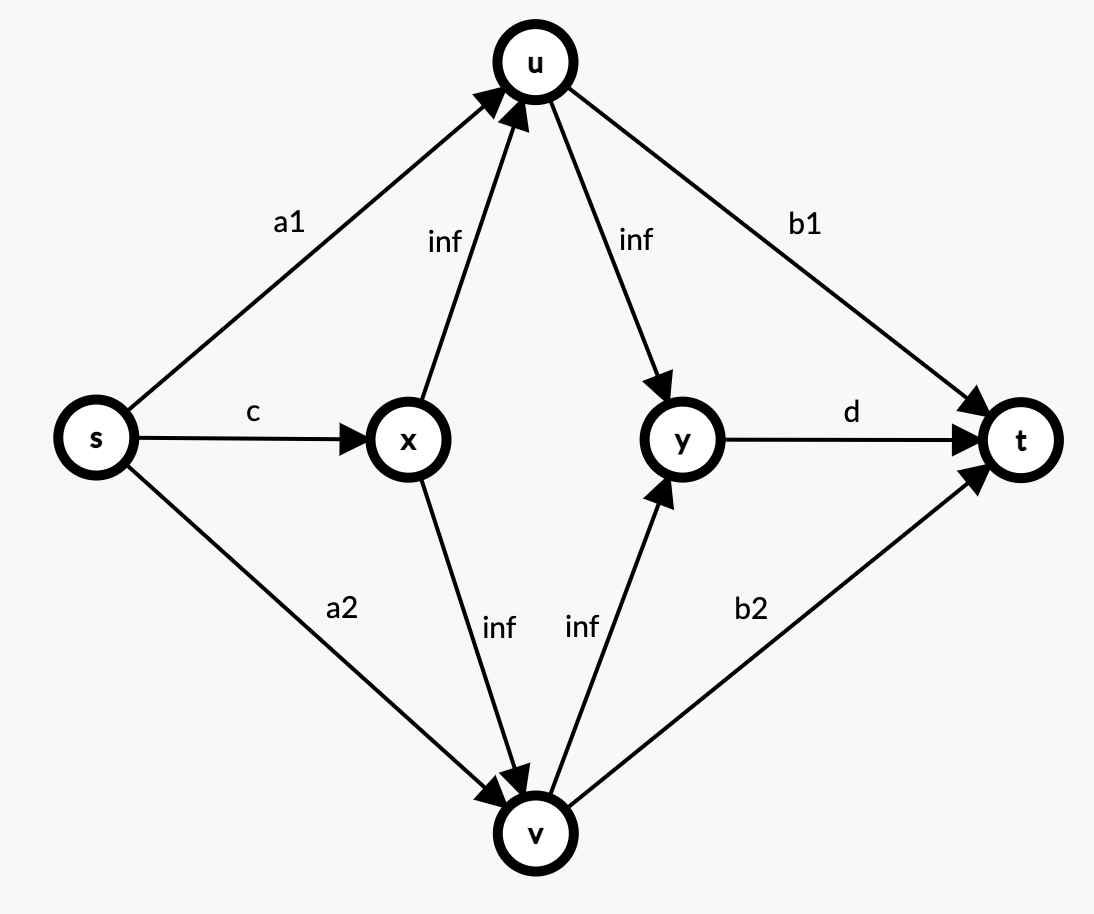
上面已经解释过了,意思就是只要两个人中,任何一个人选了文,则 理理 的额外收益就没了(被割掉)。任何一个人选了理,则 文文 的额外收益就没了(被割掉)。由此建图即可。
注意,我们计算的是 最小割,意思是 损失的最小收益,所以最终的答案(最大收益)应该是由 所有可能获得的收益 减去 最小割。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 7e4+5;
const int maxm = 5e5+5;
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
ll maxflow() {
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
return ans;
}
int a[103][103], b[103][103];
int N = 0, id[103][103];
ll sum = 0;
int main() {
cin >> n >> m;
s = 5*n*m+1, t = s+1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j], id[i][j] = ++N;
add(s, N, a[i][j]);
sum += a[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> b[i][j];
add(id[i][j], t, b[i][j]);
sum += b[i][j];
}
}
for (int i = 1; i <= n-1; i++) {
for (int j = 1; j <= m; j++) {
int aa; cin >> aa; // 文文
add(s, ++N, aa);
add(N, id[i][j], 1e9);
add(N, id[i+1][j], 1e9);
sum += aa;
}
}
for (int i = 1; i <= n-1; i++) {
for (int j = 1; j <= m; j++) {
int bb; cin >> bb; // 理理
add(++N, t, bb);
add(id[i][j], N, 1e9);
add(id[i+1][j], N, 1e9);
sum += bb;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m-1; j++) {
int aa; cin >> aa;
add(s, ++N, aa);
add(N, id[i][j], 1e9);
add(N, id[i][j+1], 1e9);
sum += aa;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m-1; j++) {
int bb; cin >> bb; // 理理
add(++N, t, bb);
add(id[i][j], N, 1e9);
add(id[i][j+1], N, 1e9);
sum += bb;
}
}
cout << sum - maxflow() << endl;
}
例7 CF1404E Bricks
题意
给定一个 $n \times m$ 的网格,每个格子要么为黑,要么为白。
定义一个 brick 为:一个长方形,要么长度为 $1$,宽度任意;要么宽度为 $1$,长度任意。
我们需要用 brick 来覆盖所有的黑色格子,要求不能覆盖到白色格子上,并且一个黑格子只能被覆盖一次。
求最少的 brick 数量?
其中,$1 \leq n,m \leq 200$,保证至少有一个黑格子。
题解
一个 brick 可以横着摆,也可以纵着摆。
所以,每个黑格子要么被一个 横brick 覆盖,要么被一个 纵brick 覆盖。
如果被 横brick 覆盖,就相当于给这个格子填上 $1$。被 纵brick 覆盖就相当于给这个格子填上 $0$。
我们会发现,如果在横方向上,有两个连续的 $1$,那么这两个格子就可以合并为一个(相当于只用了一个横brick就覆盖了它们两个),纵向同理。
问题就转化为,怎么给每个格子填上 $0/1$,使得这种合并的发生次数最多。
让合并的发生次数最多,实际上就和上一题一样了。就是定义两个相邻的格子,同时选0/1时,可以获得一些额外收益,这个收益就是合并次数。
最终的答案就是 黑格子数量 减去 合并发生次数。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
const int maxm = 7e5+5;
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
ll maxflow() {
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
return ans;
}
int grid[205][205], id[205][205], N = 0;
int main() {
fastio;
cin >> n >> m;
int sum = 0;
for (int i = 1; i <= n; i++) {
string ss; cin >> ss;
for (int j = 1; j <= m; j++) {
if (ss[j-1] == '#') grid[i][j] = 1, id[i][j] = ++N, sum++;
}
}
int tmp = sum;
s = N+1, t = s+1;
for (int i = 1; i <= N; i++) {
add(s, i, 1);
add(i, t, 1);
}
N += 3;
int delta[2][2] = {{1, 0}, {0, 1}};
int inf = 1e9;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!id[i][j]) continue;
for (int o = 0; o < 2; o++) {
int di = delta[o][0] + i, dj = delta[o][1] + j;
if (di >= 1 && di <= n && dj >= 1 && dj <= m && id[di][dj]) {
if (o == 0) { // 纵向
add(s, ++N, 1);
add(N, id[i][j], inf);
add(N, id[di][dj], inf);
sum++;
} else { // 横向
add(++N, t, 1);
add(id[i][j], N, inf);
add(id[di][dj], N, inf);
sum++;
}
}
}
}
}
cout << tmp - sum + maxflow() << endl;
}
例8 ABC193F Zebraness
题意
给定 $n \times n$ 的网格,每个格子要么为黑色,要么为白色,要么没有颜色。
现在要将所有没有颜色的格子,涂上黑色或者白色。
求最终情况下,相邻的不同色格子的最大数量。
其中,$1 \leq N \leq 100$。
题解
看起来非常像最小割的二元模型,但是有一点不太一样的在于,这里是两个相邻的,不同颜色 的格子才能产生收益。而上面两道例题,都是 相同颜色 的格子才能产生收益。
这样的话就没法建图了。
但是我们可以把问题转化一下,成为 相同颜色 的格子才能产生收益。
怎么做呢?
把这些格子分为两类,一类是 $x,y$ 坐标加起来为奇数的,另外一类是 $x,y$ 坐标加起来为偶数的。我们把其中一类格子的颜色全部反过来(如果没有颜色就不用动它)。问题就转化成 相同颜色 的格子产生收益了。
但是,这题有一些格子是已经固定好颜色了的。假如一个格子已知为白色,那么就不连 $(u,t)$ 这条边即可。并且为了保证这个格子一定选择了白色,我们连 $(s,u,inf)$。
对于黑色,就连 $(u,t,inf)$。
对于没有颜色,就连 $(s,u,1), (u,t,1)$。
然后相邻的格子仍然按照同色的套路来创建新点,连接容量为 $1$ 的边即可。
注意到本题,因为一个格子本身选择什么颜色并不提供价值。所以我们要把 总价值 中,通过选择单个格子获得的价值减掉。
所以原本 一个黑/白 格子提供的价值为 $1$,现在则为 $0$。原本一个 无色 格子提供的价值为 $2$,现在则为 $1$。相邻格子同色带来的价值不变。
最后用 总价值 减去 最小割 即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4+5;
const int maxm = 7e5+5;
int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
int dis[maxn];
bool bfs() {
queue<int> q;
memset(dis, -1, sizeof(dis));
memcpy(cur, head, sizeof(head));
dis[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] >= 0 || w == 0) continue; // visited 或者 edge 已经不存在
dis[to] = dis[u] + 1;
q.push(to);
if (to == t) return 1; // 仍然存在增广路,直接返回
}
}
return 0;
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w;
if (dis[to] != dis[u] + 1 || w == 0) continue; // 不是下一层 或者 edge已经不存在
// 否则,可以往外运输流量
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break; // 如果已经没有可以向外流的了,直接 break
}
if (out == 0) dis[u] = -1; // 说明当前节点已经不能向外运输流量了,忽略不计
return out;
}
void add(int u, int v, ll w) {
addEdge(u, v, w);
addEdge(v, u, 0);
}
ll maxflow() {
ll ans = 0;
while (bfs()) {
ans += dfs(s, 1e18);
}
return ans;
}
int arr[102][102];
int vid[102][102], vidcnt = 0;
int main() {
fastio;
cin >> n;
int N = n*n;
s = 5*N+1, t = 5*N+2;
for (int i = 1; i <= n; i++) {
string SS; cin >> SS;
for (int j = 1; j <= n; j++) {
if (SS[j-1] == 'W') arr[i][j] = 0;
if (SS[j-1] == 'B') arr[i][j] = 1;
if (SS[j-1] == '?') arr[i][j] = -1;
if (((i+j)&1) && arr[i][j] >= 0) arr[i][j] ^= 1;
vid[i][j] = ++vidcnt;
}
}
int delta[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};
ll ans = 0;
int inf = 1e9;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
int id = vid[i][j];
if (arr[i][j] == 0) {
add(s, id, inf);
}
if (arr[i][j] == 1) {
add(id, t, inf);
}
if (arr[i][j] == -1) {
add(s, id, 1), add(id, t, 1);
ans++;
}
for (int o = 0; o < 2; o++) {
int di = i + delta[o][0], dj = j + delta[o][1];
if (di >= 1 && di <= n && dj >= 1 && dj <= n) {
int did = vid[di][dj];
add(s, ++vidcnt, 1);
add(vidcnt, id, inf);
add(vidcnt, did, inf);
ans++;
add(++vidcnt, t, 1);
add(id, vidcnt, inf);
add(did, vidcnt, inf);
ans++;
}
}
}
}
ans -= maxflow();
cout << ans << endl;
}
例9 [NOI2008] 志愿者招募
题意
有 $n$ 天,每天需要 $a_i$ 个人。我们有 $m$ 种人可以招募,第 $i$ 种人会从 第 $s_i$ 天 工作到 第 $t_i$ 天,并且花费 $c_i$ 元。
求最少费用的方案,满足每天工作的人数?
其中 $1 \leq n \leq 1000, 1 \leq m \leq 10000$。
题解
区间覆盖模型,上面讲过了。
连 $(s,1,inf,0), (n+1,t,inf,0)$,同时对于每一个 $i$,连 $(i,i+1,inf-a_i,0)$。
对于每种工人,连 $(s_i, t_i + 1, inf, c_i)$。
跑最小费用最大流即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int maxm = 5e4+5;
int n,m,s,t;
struct Edge {
int to, nxt;
ll w, c;
} edges[maxm<<1];
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
void addEdge(int u, int v, ll w, ll c) {
Edge e = {v, head[u], w, c};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dis[maxn];
bool inq[maxn], vis[maxn];
bool spfa(bool mincost = true) {
queue<int> q;
memset(vis, 0, sizeof(vis)); // 这里一定要记得清空 vis (dfs要用)
memset(inq, 0, sizeof(inq));
fill(dis, dis+maxn, mincost ? 1e18 : -1e18);
memcpy(cur, head, sizeof(head)); // 当前弧优化用到的数组 cur
dis[s] = 0;
inq[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (w == 0) continue;
if ((mincost && dis[u] + c < dis[to]) || (!mincost && dis[u] + c > dis[to])) {
dis[to] = dis[u] + c;
if (!inq[to]) {
inq[to] = 1;
q.push(to);
}
}
}
}
return dis[t] != (mincost ? 1e18 : -1e18);
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
vis[u] = 1;
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (vis[to] || w == 0 || dis[to] != dis[u] + c) continue;
// 检测: 1. 是否vis过 2. 这条边是否存在 3. 是否是最短路径
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break;
}
if (out == 0) dis[u] = -1e18;
return out;
}
ll cost = 0;
ll mcmf() {
ll maxflow = 0;
while (spfa()) {
ll res = dfs(s, 1e18);
maxflow += res;
cost += res * dis[t]; // cost += (流量 * 最短路长度)
}
return maxflow;
}
void add(int u, int v, ll w, ll c) {
addEdge(u,v,w,c);
addEdge(v,u,0,-c);
}
int main() {
cin >> n >> m;
s = n+2, t = n+3;
ll inf = 4e9;
add(s, 1, inf, 0);
for (int i = 1; i <= n; i++) {
ll a; cin >> a;
add(i, i+1, inf-a, 0);
}
add(n+1, t, inf, 0);
while (m--) {
int l,r,c; cin >> l >> r >> c;
add(l, r+1, inf, c);
}
ll maxflow = mcmf();
cout << cost << endl;
}
例10 洛谷P3358 最长k可重区间集问题
题意
给定 $n$ 个左闭右开的区间,请选出一些区间,使得直线上任意一点,被覆盖的次数不超过 $k$ 次。
求这些区间的长度之和的最大值。
其中,$1 \leq n \leq 500, 1\leq k \leq 3$,保证每个区间的左右端点为整数,且长度大于等于 $1$。
题解
由于区间左右端点可能会有很大的值,甚至负数,所以第一步肯定是离散化。
如何限定被覆盖的次数不超过 $k$ 次?
我们只要限制 流量 最多为 $k$ 即可。
对于区间,仍然是和上面一样的套路。
所以建图:
离散化出直线上的关键点,将它们作为节点,编号为 $1, 2, …, N$。
对于 $\forall i \in [1,N-1]$,连 $(i,i+1,inf,0)$。
同时连 $(s,1,k,0), (N,t,k,0)$。
对于每个区间 $[l,r]$,连接 $(a_l, a_r, 1, r-l)$,其中 $a_l$ 就是 $l$ 在离散化之后对应的节点。
跑一个最大费用最大流即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 5e5+5;
int n,m,s,t,k;
struct Edge {
int to, nxt;
ll w, c;
} edges[maxm<<1];
int head[maxn], ecnt = 2, cur[maxn]; // ecnt 从 2 开始,方便取反向边
void addEdge(int u, int v, ll w, ll c) {
Edge e = {v, head[u], w, c};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll dis[maxn];
bool inq[maxn], vis[maxn];
bool spfa(bool mincost = true) {
queue<int> q;
memset(vis, 0, sizeof(vis)); // 这里一定要记得清空 vis (dfs要用)
memset(inq, 0, sizeof(inq));
fill(dis, dis+maxn, mincost ? 1e18 : -1e18);
memcpy(cur, head, sizeof(head)); // 当前弧优化用到的数组 cur
dis[s] = 0;
inq[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
inq[u] = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (w == 0) continue;
if ((mincost && dis[u] + c < dis[to]) || (!mincost && dis[u] + c > dis[to])) {
dis[to] = dis[u] + c;
if (!inq[to]) {
inq[to] = 1;
q.push(to);
}
}
}
}
return dis[t] != (ll)(mincost ? 1e18 : -1e18);
}
ll dfs(int u, ll in) {
if (u == t) return in; // 如果已经运到了终点,直接返回入量
vis[u] = 1;
ll out = 0;
for (int e = cur[u]; e; e = edges[e].nxt) {
cur[u] = e;
int to = edges[e].to;
ll w = edges[e].w, c = edges[e].c;
if (vis[to] || w == 0 || dis[to] != dis[u] + c) continue;
// 检测: 1. 是否vis过 2. 这条边是否存在 3. 是否是最短路径
ll res = dfs(to, min(in, w));
in -= res;
out += res;
edges[e].w -= res;
edges[e^1].w += res;
if (in == 0) break;
}
if (out == 0) dis[u] = -1e18;
return out;
}
ll cost = 0;
ll mcmf() {
ll maxflow = 0;
while (spfa(false)) {
ll res = dfs(s, 1e18);
maxflow += res;
cost += res * dis[t]; // cost += (流量 * 最短路长度)
}
return maxflow;
}
void add(int u, int v, ll w, ll c) {
addEdge(u,v,w,c);
addEdge(v,u,0,-c);
}
struct Segment {
int l,r;
} seg[505];
set<int> bound;
map<int, int> mp; // map boundary to index
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> seg[i].l >> seg[i].r;
bound.insert(seg[i].l);
bound.insert(seg[i].r);
}
int N = 0; // 线段的数量
for (int a : bound) {
mp[a] = ++N;
}
for (int i = 1; i <= n; i++) {
int l = mp[seg[i].l], r = mp[seg[i].r];
add(l, r, 1, seg[i].r - seg[i].l);
}
s = N+1, t = s+1;
for (int i = 1; i <= N; i++) {
if (i < N) add(i, i+1, 2e9, 0);
}
add(s, 1, k, 0);
add(N, t, k, 0);
ll maxflow = mcmf();
cout << cost << endl;
}
例11 HDU1853 Cyclic Tour
题意
给定 $n$ 个点,$m$ 个边的有向图,每个边有边权 $c_i$,求是否存在一些环,使得每个节点被 exactly 一个环使用,并且使得这些环的边权和最小?
如果不存在,输出 $-1$。
其中,$n \leq 100, m \leq 10^4$。
题解
拆点,把每个点拆成入点和出点。
出点 $u$ 放在左侧,入点 $u+n$ 放在右侧,得到一个二分图。
对于每一条原图中的边 $(u,v)$ 链接 $(u, v+n, 1, c)$,其中 $c$ 是边权。
然后链接 $(s, u, 1, 0), (u+n, t, 1, 0)$。
最后跑最小费用流即可。如果满足答案则最大流 $=n$。
• 证明:这样保证了每个点的出度和入度均为 $1$,这说明它们一定在一个环上。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int main() {
int n, m;
while (cin >> n >> m) {
for (int i = 1; i <= m; i++) {
int u, v, c;
cin >> u >> v >> c;
flow.add(u, v+n, 1, c);
}
flow.s = 2*n + 1, flow.t = 2*n + 2;
for (int i = 1; i <= n; i++) {
flow.add(flow.s, i, 1, 0);
flow.add(i+n, flow.t, 1, 0);
}
ll maxflow = flow.mcmf(true); // 最小费用流,返回最大流
if (maxflow != n) {
cout << -1 << "\n";
} else {
cout << flow.cost << "\n";
}
flow.clear();
}
}
例12 NAQ2022 J. Room Evacuation
题意
给定一个 $n \times m$ 的网格,每个位置要么是 P 代表一个人,E 代表一个出口,# 代表一个障碍物,. 代表一个空地。
现在给定 $T$ 秒,每一秒,所有人都可以往相邻的格子移动一格,但任意时间,同一个格子上只能站一个人。
如果一个人来到了一个出口,那么他就安全了,并且在下一秒将会消失在网格中。出口也只能同时站一个人。
求在规定的 $T$ 秒内,最多有多少个人能安全?
其中,$n,m \leq 20, 1\leq T \leq 200$。
题解
一看数据范围就知道是网络流,并且 $T \leq 200$,为了限制每一秒,一个格子上只能站一个人,我们将图拆成 $T$ 层(复制 $T$ 份),像 $\forall i, t=i$ 连边到 $t=i+1$ 的。
然后 $s$ 向所有 $T=0$ 的 P 连边,所有的 $T=0,1,…$ 的 E 向 $t$ 连边,所有边的容量为 $1$,然后相邻位置 $t=i$ 连边到 $t=i+1$ 的。
• 然后需要注意,每个点需要限制流量为 $1$,这是防止多个点通过同一个点走到其他位置,一个经典例子是
#E#
PPE
#P#
限制流量的方法就是拆点,拆为 in, out。
代码
#include <bits/stdc++.h>
using namespace std;
int id[22][22], cid = 0;
vector<int> pe, ex;
int d[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
int in_id(int x) {
return x;
}
int out_id(int x) {
return x + (T+2) * n * m;
}
int main() {
cin >> n >> m >> T;
for (int i = 1; i <= n; i++) {
string ss; cin >> ss;
for (int j = 1; j <= m; j++) {
grid[i][j] = ss[j-1];
if (grid[i][j] != '#') {
id[i][j] = ++cid;
}
if (grid[i][j] == 'P') {
pe.push_back(id[i][j]);
}
if (grid[i][j] == 'E') {
ex.push_back(id[i][j]);
}
}
}
s = maxn-5, t = maxn-4;
for (int tt = 0; tt < T; tt++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!id[i][j]) continue;
int id1 = id[i][j] + tt * n * m;
for (int o = 0; o < 4; o++) {
int ni = i + d[o][0], nj = j + d[o][1];
if (ni >= 1 && ni <= n && nj >= 1 && nj <= m && grid[ni][nj] != '#') {
int id2 = id[ni][nj] + (tt+1) * n * m;
// if (grid[ni][nj] != 'E')
// assert(id1 <= id2);
add(out_id(id1), in_id(id2), 1);
// add(id1, id2, 1);
}
}
if (tt == 0 && grid[i][j] == 'P') {
add(s, in_id(id1), 1);
}
if (grid[i][j] == 'E') {
add(out_id(id1), t, 1);
}
add(out_id(id1), in_id(id1+n*m), 1);
add(in_id(id1), out_id(id1), 1);
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int id1 = id[i][j] + T * n * m;
add(in_id(id1), out_id(id1), 1);
if (grid[i][j] == 'E') {
add(out_id(id1), t, 1);
}
}
}
cout << maxflow() << endl;
}
例13 洛谷P4126 [AHOI2009]最小割
题意
给一张有向图和 $s,t$,对每一条边回答它是否为可行边,是否为必要边。
题解
上面解释了,注意判断的时候判断 “满流与否”。
代码
#include <bits/stdc++.h>
using namespace std;
// 网络流部分省略
int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn];
bool in[maxn]; // instack or not
int st[maxn], tail = -1;
void dfs(int u) {
in[u] = 1;
st[++tail] = u;
dfn[u] = low[u] = ++id;
for (int e = head[u]; e; e = edges[e].nxt) {
if (!edges[e].w) continue; // 残量网络
int to = edges[e].to;
if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);
if (!dfn[to]) {
dfs(to);
low[u] = min(low[u], low[to]);
}
}
if (dfn[u] == low[u]) {
from[u] = ++scc;
sz[scc] = 1;
while (tail >= 0 && st[tail] != u) {
int cur = st[tail];
from[cur] = from[u];
sz[scc]++;
tail--;
in[cur] = 0;
}
tail--;
in[u] = 0;
}
}
void tarjan() {
for (int i = 1; i <= n; i++) {
if (!dfn[i]) dfs(i);
}
}
int main() {
cin >> n >> m >> s >> t;
for (int i = 1; i <= m; i++) {
int u,v; ll w;
cin >> u >> v >> w;
add(u, v, w);
}
maxflow();
tarjan();
for (int e = 2; e < ecnt; e += 2) {
int u = edges[e].from, v = edges[e].to;
cout << (edges[e].w == 0 && from[u] != from[v]) << " "; // 判断满流
cout << (edges[e].w == 0 && from[u] == from[s] && from[v] == from[t]) << "\n"; // 判断满流
}
}
