多项式全家桶
Contents
模版
多项式全家桶(比较精简的版本,利用了Z)
template<class T>
T qpow(T a, int b) {
T res = 1;
while (b) {
if (b & 1) res *= a;
a *= a;
b >>= 1;
}
return res;
}
int norm(int x) {
if (x < 0) {
x += mod;
}
if (x >= mod) {
x -= mod;
}
return x;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
Z(ll x) : x(norm((int)(x % mod))) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(mod - x));
}
Z inv() const {
assert(x != 0);
return qpow(*this, mod - 2);
}
Z &operator*=(const Z &rhs) {
x = (ll)(x) * rhs.x % mod;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
ll v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
std::vector<int> rev;
std::vector<Z> roots{0, 1};
void dft(std::vector<Z> &a) {
int n = a.size();
if (int(rev.size()) != n) {
int k = __builtin_ctz(n) - 1;
rev.resize(n);
for (int i = 0; i < n; i++) {
rev[i] = rev[i >> 1] >> 1 | (i & 1) << k;
}
}
for (int i = 0; i < n; i++) {
if (rev[i] < i) {
std::swap(a[i], a[rev[i]]);
}
}
if (int(roots.size()) < n) {
int k = __builtin_ctz(roots.size());
roots.resize(n);
while ((1 << k) < n) {
Z e = qpow(Z(3), (mod - 1) >> (k + 1));
for (int i = 1 << (k - 1); i < (1 << k); i++) {
roots[2 * i] = roots[i];
roots[2 * i + 1] = roots[i] * e;
}
k++;
}
}
for (int k = 1; k < n; k *= 2) {
for (int i = 0; i < n; i += 2 * k) {
for (int j = 0; j < k; j++) {
Z u = a[i + j];
Z v = a[i + j + k] * roots[k + j];
a[i + j] = u + v;
a[i + j + k] = u - v;
}
}
}
}
void idft(std::vector<Z> &a) {
int n = a.size();
std::reverse(a.begin() + 1, a.end());
dft(a);
Z inv = (1 - mod) / n;
for (int i = 0; i < n; i++) {
a[i] *= inv;
}
}
struct Poly {
std::vector<Z> a;
Poly() {}
Poly(const int n) { resize(n); }
Poly(const std::vector<Z> &a) : a(a) {}
Poly(const std::initializer_list<Z> &a) : a(a) {}
int size() const {
return a.size();
}
void resize(int n) {
a.resize(n);
}
Z operator[](int idx) const {
if (idx < size()) {
return a[idx];
} else {
return 0;
}
}
Z &operator[](int idx) {
return a[idx];
}
Poly mulxk(int k) const {
auto b = a;
b.insert(b.begin(), k, 0);
return Poly(b);
}
Poly modxk(int k) const {
k = std::min(k, size());
return Poly(std::vector<Z>(a.begin(), a.begin() + k));
}
Poly divxk(int k) const {
if (size() <= k) {
return Poly();
}
return Poly(std::vector<Z>(a.begin() + k, a.end()));
}
friend Poly operator+(const Poly &a, const Poly &b) {
std::vector<Z> res(std::max(a.size(), b.size()));
for (int i = 0; i < int(res.size()); i++) {
res[i] = a[i] + b[i];
}
return Poly(res);
}
friend Poly operator-(const Poly &a, const Poly &b) {
std::vector<Z> res(std::max(a.size(), b.size()));
for (int i = 0; i < int(res.size()); i++) {
res[i] = a[i] - b[i];
}
return Poly(res);
}
friend Poly operator*(Poly a, Poly b) {
if (a.size() == 0 || b.size() == 0) {
return Poly();
}
int sz = 1, tot = a.size() + b.size() - 1;
while (sz < tot) {
sz *= 2;
}
a.a.resize(sz);
b.a.resize(sz);
dft(a.a);
dft(b.a);
for (int i = 0; i < sz; ++i) {
a.a[i] = a[i] * b[i];
}
idft(a.a);
a.resize(tot);
return a;
}
friend Poly operator*(Z a, Poly b) {
for (int i = 0; i < int(b.size()); i++) {
b[i] *= a;
}
return b;
}
friend Poly operator*(Poly a, Z b) {
for (int i = 0; i < int(a.size()); i++) {
a[i] *= b;
}
return a;
}
friend Poly operator*(Poly a, int b) {
return operator*(a, Z(b));
}
Poly &operator+=(Poly b) {
return (*this) = (*this) + b;
}
Poly &operator-=(Poly b) {
return (*this) = (*this) - b;
}
Poly &operator*=(Poly b) {
return (*this) = (*this) * b;
}
Poly deriv() const {
if (a.empty()) {
return Poly();
}
std::vector<Z> res(size() - 1);
for (int i = 0; i < size() - 1; ++i) {
res[i] = (i + 1) * a[i + 1];
}
return Poly(res);
}
Poly integr() const {
std::vector<Z> res(size() + 1);
for (int i = 0; i < size(); ++i) {
res[i + 1] = a[i] / (i + 1);
}
return Poly(res);
}
Poly inv(int m) const {
Poly x{a[0].inv()};
int k = 1;
while (k < m) {
k *= 2;
x = (x * (Poly{2} - modxk(k) * x)).modxk(k);
}
return x.modxk(m);
}
Poly log(int m) const {
return (deriv() * inv(m)).integr().modxk(m);
}
Poly exp(int m) const {
Poly x{1};
int k = 1;
while (k < m) {
k *= 2;
x = (x * (Poly{1} - x.log(k) + modxk(k))).modxk(k);
}
return x.modxk(m);
}
Poly pow(int k, int m) const {
int i = 0;
while (i < size() && a[i].val() == 0) {
i++;
}
if (i == size() || 1LL * i * k >= m) {
return Poly(std::vector<Z>(m));
}
Z v = a[i];
auto f = divxk(i) * v.inv();
return (f.log(m - i * k) * k).exp(m - i * k).mulxk(i * k) * qpow(v, k);
}
Poly sqrt(int m) const {
Poly x{1};
int k = 1;
while (k < m) {
k *= 2;
x = (x + (modxk(k) * x.inv(k)).modxk(k)) * ((mod + 1) / 2);
}
return x.modxk(m);
}
Poly mulT(Poly b) const {
if (b.size() == 0) {
return Poly();
}
int n = b.size();
std::reverse(b.a.begin(), b.a.end());
return ((*this) * b).divxk(n - 1);
}
std::vector<Z> eval(std::vector<Z> x) const {
if (size() == 0) {
return std::vector<Z>(x.size(), 0);
}
const int n = std::max(int(x.size()), size());
std::vector<Poly> q(4 * n);
std::vector<Z> ans(x.size());
x.resize(n);
std::function<void(int, int, int)> build = [&](int p, int l, int r) {
if (r - l == 1) {
q[p] = Poly{1, -x[l]};
} else {
int m = (l + r) / 2;
build(2 * p, l, m);
build(2 * p + 1, m, r);
q[p] = q[2 * p] * q[2 * p + 1];
}
};
build(1, 0, n);
std::function<void(int, int, int, const Poly &)> work = [&](int p, int l, int r, const Poly &num) {
if (r - l == 1) {
if (l < int(ans.size())) {
ans[l] = num[0];
}
} else {
int m = (l + r) / 2;
work(2 * p, l, m, num.mulT(q[2 * p + 1]).modxk(m - l));
work(2 * p + 1, m, r, num.mulT(q[2 * p]).modxk(r - m));
}
};
work(1, 0, n, mulT(q[1].inv(n)));
return ans;
}
};
多项式全家桶(其他人的,很快)
using ll = long long;
// END OF HEADER
#define ACM_MOD 998244353
const int P = ACM_MOD;
#ifdef ACM_MOD
int qpow(ll a, ll b = ACM_MOD - 2, ll m = ACM_MOD) {
#else
int qpow(ll a, ll b, ll m) {
#endif
ll ret = m != 1;
for (; b; b >>= 1) {
if (b & 1)
ret = ret * a % m;
a = a * a % m;
}
return ret;
}
template <typename T> T tpow(T a, ll b) {
T ret;
for (; b; b >>= 1) {
if (b & 1)
ret = ret * a;
a = a * a;
}
return ret;
}
#define ACM_MATH_CIPOLLA_H
namespace Qresidue {
ll legendre(ll a, ll p) {
return qpow(a, (p - 1) / 2, p);
}
ll find_a(ll n, ll p) {
for (ll a = 0; a < p; a++) {
ll i = (a * a - n + p) % p;
if (qpow(i, (p - 1) / 2, p) == p - 1)
return a;
}
return -1;
}
ll P, I;
struct expnum {
ll a = 1, b = 0;
};
expnum operator*(expnum i1, expnum i2) {
return expnum{(i1.a * i2.a + i1.b * i2.b % P * I) % P, (i1.b * i2.a + i1.a * i2.b) % P};
}
std::pair<int, int> Cipolla(ll n, ll _p) {
P = _p;
if (n % P == 0) // 不互质的情形
return {0, 0};
if (legendre(n, P) != 1)
return {-1, -1}; // 返回-1表示无解
ll a = find_a(n, P);
I = (a * a - n + P) % P;
ll ans = tpow(expnum{a, 1}, (P + 1) / 2).a % P;
if (2 * ans > P)
ans = P - ans;
return {ans, P - ans};
}
}; // namespace Qresidue
std::pair<int, int> Cipolla(ll n, ll p) {
return Qresidue::Cipolla(n, p);
}
inline int mo(int n) {
return n >= P ? n - P : n;
}
inline int &momo(int &n) {
return n >= P ? n -= P : n;
}
struct m32 {
int v = 0;
m32(int _v = 0) {
v = _v;
}
m32 &operator=(const int &m) {
v = m;
return *this;
}
m32 &operator+=(const m32 &m) {
v = (v += m.v) >= P ? v - P : v;
return *this;
}
m32 &operator-=(const m32 &m) {
v = (v -= m.v) < 0 ? v + P : v;
return *this;
}
m32 operator-() const {
return v == 0 ? 0 : P - v;
}
m32 &operator*=(const m32 &m) {
v = ll(v) * m.v % P;
return *this;
}
m32 operator+(const m32 &m) const {
return m32(*this) += m;
}
m32 operator-(const m32 &m) const {
return m32(*this) -= m;
}
m32 operator*(const m32 &m) const {
return m32(*this) *= m;
}
m32 inv() const {
return qpow(v);
}
m32 pow(int n) const {
return qpow(v, n, P);
}
m32 sqrt() const {
#ifdef ACM_MATH_CIPOLLA_H
return Cipolla(v, P).first;
#else
return 1;
#endif
}
};
inline int get_lim(int n) {
int m = 1;
while (m < n)
m *= 2;
return m;
}
struct Poly : std::vector<m32> {
using vector::vector;
bool isNTT = false;
Poly(Poly::const_iterator pi, int len) : Poly(pi, pi + len) {
}
Poly rev() const {
return Poly(rbegin(), rend());
}
int deg() const {
return size();
}
Poly cut(int m) const {
return Poly(begin(), begin() + min(deg(), m));
}
Poly &resize(int m) {
vector::resize(m);
return *this;
}
Poly &fillZeroL(int t) {
fill_n(begin(), t / 2, 0);
return *this;
}
Poly &fillZeroH(int t) {
fill_n(begin() + t / 2, t / 2, 0);
return *this;
}
friend Poly operator+(Poly f, Poly g);
friend Poly operator-(Poly f, Poly g);
friend Poly operator*(Poly f, Poly g);
Poly &ntt(int m);
Poly &nttD(int m);
Poly &intt(int m);
Poly &invD(Poly f2, Poly nx, int t);
Poly inv() const;
Poly div(Poly g) const;
Poly deriv() const;
Poly integr() const;
Poly ln() const;
Poly exp() const;
Poly sqrt() const;
Poly pow(int k) const;
Poly mod() const;
};
Poly w, Inv;
void pre_w(int n, int w0 = 3) {
static int lim = (w = {1, 1}, 2);
n = get_lim(n);
if (n <= lim)
return;
w.resize(n);
for (int l = lim; l < n; l *= 2) {
m32 p = m32(w0).pow((P - 1) / l / 2);
for (int i = 0; i < l; i += 2) {
w[(l + i)] = w[(l + i) / 2];
w[l + i + 1] = w[l + i] * p;
}
}
lim = n;
}
void pre_inv(int n) {
static int LIM = (Inv = {1, 1}, 2);
if (n <= LIM)
return;
Inv.resize(n);
for (int i = LIM; i < n; i++) {
Inv[i] = Inv[P % i] * (P - P / i);
}
LIM = n;
}
static int ntt_size = 0;
void ntt(Poly::iterator f, int deg) {
pre_w(deg);
ntt_size += deg;
for (int l = deg >> 1; l; l >>= 1)
for (auto fi = f; fi - f < deg; fi += l * 2)
for (int j = 0; j < l; j++) {
auto x = fi[j] + fi[j + l];
fi[j + l] = w[j + l] * (fi[j] - fi[j + l]);
fi[j] = x;
}
}
void intt(Poly::iterator f, int deg) {
ntt_size += deg;
for (int l = 1; l < deg; l <<= 1)
for (auto fi = f; fi - f < deg; fi += l * 2)
for (int j = 0; j < l; j++) {
auto x = fi[j], y = fi[j + l] * w[j + l];
fi[j] = x + y, fi[j + l] = x - y;
}
const auto deg_inv = P - (P - 1) / deg;
for (int i = 0; i < deg; i++)
f[i] *= deg_inv;
std::reverse(f + 1, f + deg);
}
void nttD(Poly::iterator f, int n) {
std::copy_n(f, n, f + n);
intt(f + n, n);
for (int i = n; i < n * 2; i++)
f[i] *= w[i];
ntt(f + n, n);
}
Poly &Poly::ntt(int n) {
if (!isNTT) {
resize(n);
::ntt(begin(), n);
isNTT = true;
}
return *this;
}
Poly &Poly::intt(int m) {
::intt(begin(), m);
isNTT = false;
return *this;
}
Poly &Poly::nttD(int n) {
resize(n * 2);
::nttD(begin(), n);
return *this;
}
Poly &mul(Poly &f, Poly &g, int t) {
f.ntt(t), g.ntt(t);
for (int i = 0; i < t; i++)
f[i] *= g[i];
return f.intt(t);
}
Poly operator*(Poly f, Poly g) {
if (f.deg() < g.deg())
swap(f, g);
int t = f.deg() + g.deg() - 1;
return mul(f, g, get_lim(t)).cut(t);
}
Poly operator+(Poly f, Poly g) {
if (f.deg() < g.deg())
std::swap(f, g);
for (int i = 0; i < g.deg(); i++)
f[i] += g[i];
return f;
}
Poly operator-(Poly f, Poly g) {
for (auto &i : g)
i = -i;
return std::move(f) + g;
}
m32 mulAt(const Poly f, const Poly g, int u) {
int n = f.deg() - 1, m = g.deg() - 1;
m32 ans = 0;
for (int i = std::max(0, u - m); i <= std::min(u, n); i++)
ans += f[i] * g[u - i];
return ans;
}
struct PolySemi {
using iter = Poly::iterator;
const int B = 16;
int n, m;
Poly F, v1, v2, ret;
std::function<void(int, m32 &)> relax;
void run(int l, int r, iter g, iter h) {
if (r - l <= 64) {
for (int i = l; i < r; ++i) {
relax(i, ret[i]);
for (int j = i + 1; j < r; ++j)
ret[j] += ret[i] * F[j - i];
}
return;
}
int len = (r - l) / B, k = 2 * len;
iter tg[B], th[B];
for (int i = 0; i < B - 1; i++)
tg[i] = g + i * k, th[i] = h + i * k;
if (l == 0) {
for (int i = 0; i < B - 1; i++) {
if ((i + 1) * len >= n)
break;
copy_n(F.begin() + i * len, k, th[i]);
ntt(th[i], k);
}
}
for (int i = 0; i < B; i++) {
auto u = l + i * len;
if (u >= n)
break;
Poly s(k);
for (int j = 0; j < i; j++)
for (int t = 0; t < k; t++)
s[t] += tg[j][t] * th[i - j - 1][t];
s.intt(k);
for (int t = 0; t < len; t++)
ret[t + u] += s[t + len];
run(u, u + len, g + k * B, h + k * B);
if (i != B - 1) {
copy_n(ret.begin() + u, len, tg[i]);
ntt(tg[i], k);
}
}
fill_n(g, k * B, 0);
}
PolySemi(Poly f) : F(f) {
n = F.size();
m = get_lim(n);
F.resize(m), ret.resize(m);
v1.resize(m * 4), v2.resize(m * 4);
ret[0] = 1;
}
Poly exp() {
pre_inv(m);
for (int i = 0; i < n; i++)
F[i] *= i;
relax = [&](int i, m32 &ri) {
ret[i] = i == 0 ? 1 : ret[i] * Inv[i];
};
run(0, m, v1.begin(), v2.begin());
return ret.cut(n);
}
Poly inv() {
m32 iv = F[0].inv();
relax = [&](int i, m32 &ri) {
ri = i == 0 ? iv : -ri * iv;
};
run(0, m, v1.begin(), v2.begin());
return ret.cut(n);
}
Poly quo(Poly h) { // 注意是 h / f
h.resize(m);
m32 iv = F[0].inv();
relax = [&](int i, m32 &ri) {
ret[i] = i == 0 ? h[0] * iv : (h[i] - ret[i]) * iv;
};
run(0, m, v1.begin(), v2.begin());
return ret.cut(n);
}
};
Poly &Poly::invD(Poly f2, Poly nx, int t) {
mul(f2, nx, t).fillZeroL(t); // 6E
mul(f2, nx, t); // 4E
resize(t);
for (int i = t / 2; i < t; i++)
(*this)[i] = -f2[i];
return *this;
}
Poly Poly::inv() const { // 10E
Poly x = {front().inv()};
if (deg() == 1)
return x;
int lim = get_lim(deg());
for (int t = 2; t <= lim; t <<= 1)
x.invD(cut(t), x.cut(t), t);
return x.cut(deg());
}
Poly Poly::div(Poly g) const {
return PolySemi(g.resize(deg())).quo(*this);
}
Poly Poly::deriv() const {
Poly f(deg() - 1);
for (int i = 1; i < deg(); i++)
f[i - 1] = (*this)[i] * i;
return f;
}
Poly Poly::integr() const {
Poly f(deg() + 1);
pre_inv(deg() + 1);
for (int i = deg(); i > 0; --i)
f[i] = (*this)[i - 1] * Inv[i];
return f;
}
Poly Poly::ln() const {
return deriv().div(*this).integr();
}
Poly Poly::exp() const {
return PolySemi(*this).exp();
}
Poly Poly::sqrt() const { // 11E
Poly x = {front().sqrt()}, g = x.inv(), ng = g;
for (int t = 2; t < deg() * 2; t <<= 1) {
const Poly &h = *this;
Poly f = x;
if (t >= 4) {
g.invD(f.ntt(t / 2), ng, t / 2); // 3E
}
mul(f, f, t / 2); // 1E
f.resize(t);
for (int i = t / 2; i < std::min(h.deg(), t); i++)
f[i] = h[i - t / 2] + h[i] - f[i - t / 2];
ng = g;
mul(f.fillZeroL(t), ng, t); // 6E
x.resize(t);
for (int i = t / 2; i < t; i++)
x[i] = f[i] * ((P + 1) / 2);
}
return x.cut(size());
}
Poly Poly::pow(int k) const {
Poly f = ln();
for (int i = 0; i < size(); i++)
f[i] *= k;
return f.exp();
}
// 计算最大连续 <= k 的情况数
// f(x) = 1+x+x^2+...+x^k
m32 cal(ll n, ll m, ll k) {
if (k > m || m > n) return 0;
if (k == 0) return (m == 0);
Poly f(1e5+5, 0);
n = n - m + 1;
for (int i = 0; i <= k; i++) f[i] = 1;
f = f.pow(n);
return f[m];
}
ll n,m,k;
int main() {
cin >> n >> m >> k;
if (k == 0) {
if (m > 0) cout << "0\n";
else cout<<"1\n";
}
else if(m>n) cout<<"0\n";
else cout << (cal(n,m,k) - cal(n,m,k-1)).v << "\n";
cout.flush();
return 0;
}
多项式全家桶(自用,很慢)
const int mod = 998244353;
const int maxn = (1<<22) + 5;
struct NTT {
const ll g = 3, invg = inv(g); // mod = 998244353
inline ll qpow(ll a, ll b) {
ll res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
inline ll inv(ll a) {
return qpow(a, mod-2);
}
void rearrange(ll a[], const int n) {
static int rev[maxn]; // maxn > deg(h) 且 maxn 为 2的k次方 + 5
for (int i = 1; i <= n; i++) {
rev[i] = rev[i >> 1] >> 1;
if (i & 1) rev[i] |= (n >> 1);
}
for (int i = 1; i < n; i++) {
if (i < rev[i]) swap(a[i], a[rev[i]]); // 保证每对数字只翻转一次
}
}
void ntt(ll a[], const int n, int on) {
rearrange(a, n);
for (int k = 2; k <= n; k <<= 1) { // 模拟分治的合并过程
ll wn = qpow(on == 1 ? g : invg, (mod-1)/k);
for (int i = 0; i < n; i += k) {
ll w = 1;
for (int j = i; j < i + (k>>1); j++) {
ll x = a[j], y = w * a[j+(k>>1)] % mod;
a[j] = (x + y) % mod;
a[j+(k>>1)] = (x - y + mod) % mod;
w = w * wn % mod;
}
}
}
if (on == -1) {
ll invn = inv(n);
for (int i = 0; i < n; i++) a[i] = a[i] * invn % mod;
}
}
} ntt;
// calculate h(x) = f(x) * g(x), n1 = deg(f) + 1, n2 = deg(g) + 1
void poly_multiply(ll f[], int n1, ll g[], int n2, ll h[]) {
static ll F[maxn], G[maxn];
int n = 1;
n1--, n2--;
while (n <= n1 + n2) n <<= 1; // deg(h) = n1 + n2
for (int i = 0; i <= n1; i++) F[i] = f[i];
for (int i = 0; i <= n2; i++) G[i] = g[i];
for (int i = n1+1; i < n; i++) F[i] = 0;
for (int i = n2+1; i < n; i++) G[i] = 0;
memset(h, 0, sizeof(ll) * n);
ntt.ntt(F, n, 1); // 注意这里用的是 n (不是 n1)
ntt.ntt(G, n, 1);
for (int i = 0; i < n; i++) h[i] = F[i] * G[i] % mod;
ntt.ntt(h, n, -1);
}
// calculate f^{-1}, store it into g[]
// m = deg(f) + 1
void poly_inverse(ll f[], ll g[], const int m) {
if (m == 1) {
g[0] = ntt.inv(f[0]); // 应该改为二次剩余
return;
}
static ll F[maxn];
poly_inverse(f, g, (m+1)>>1);
int n = 1;
while (n <= ((m-1)<<1)) n <<= 1; // 因为 deg(h) = (m-1) * 2
for (int i = 0; i < m; i++) F[i] = f[i];
for (int i = m; i < n; i++) F[i] = 0;
ntt.ntt(F, n, 1);
ntt.ntt(g, n, 1);
for (int i = 0; i < n; i++) {
g[i] = g[i] * ((2LL - g[i] * F[i] % mod + mod) % mod) % mod;
}
ntt.ntt(g, n, -1);
for (int i = m; i < n; i++) g[i] = 0;
}
// get f'(x), store it into g[]
// n = deg(f) + 1
inline void poly_derivatives(ll f[], ll g[], const int n) {
for (ll i = 1; i < n; i++) {
g[i-1] = f[i] * i % mod;
}
g[n-1] = 0;
}
// get integral f(x)dx, store it into g[]
// n = deg(f) + 1
inline void poly_integral(ll f[], ll g[], const int n) {
for (ll i = n-1; i >= 1; i--) {
g[i] = f[i-1] * ntt.inv(i) % mod;
}
g[0] = 0;
}
// get ln(f(x)), store it into g[]
// n = deg(f) + 1
void poly_ln(ll f[], ll g[], const int n) {
static ll invf[maxn], deriv_f[maxn];
memset(invf, 0, sizeof(invf));
memset(deriv_f, 0, sizeof(deriv_f));
poly_inverse(f, invf, n);
poly_derivatives(f, deriv_f, n);
poly_multiply(deriv_f, n, invf, n, g);
poly_integral(g, g, n);
}
// get e^f(x), store it into g[]
// m = deg(f) + 1
void poly_exp(ll f[], ll g[], const int m) {
static ll F[maxn], G[maxn], lng[maxn];
if (m == 1) {
g[0] = 1;
return;
}
poly_exp(f, g, (m+1) >> 1);
int n = 1;
while (n <= ((m-1)<<1)) n <<= 1;
for (int i = 0; i < m; i++) F[i] = f[i], G[i] = g[i];
for (int i = m; i < n; i++) F[i] = 0, G[i] = 0, lng[i] = 0;
poly_ln(g, lng, m);
ntt.ntt(F, n, 1);
ntt.ntt(G, n, 1);
ntt.ntt(lng, n, 1);
for (int i = 0; i < n; i++) {
g[i] = G[i] * ((1LL - lng[i] + F[i] + mod) % mod) % mod;
}
ntt.ntt(g, n, -1);
for (int i = m; i < n; i++) g[i] = 0;
}
// given f(x), calculate g(x), such that g(x)^2 = f(x)
// m = deg(f) + 1
void poly_sqrt(ll f[], ll g[], const int m) {
static ll F[maxn], G[maxn], invG[maxn];
if (m == 1) {
g[0] = 1;
return;
}
poly_sqrt(f, g, (m+1) >> 1);
int n = 1;
while (n <= ((m-1)<<1)) n <<= 1;
for (int i = 0; i < m; i++) F[i] = f[i], G[i] = g[i], invG[i] = 0;
for (int i = m; i < n; i++) F[i] = 0, G[i] = 0, invG[i] = 0;
poly_inverse(G, invG, m);
poly_multiply(f, m, invG, m, g);
for (int i = 0; i < m; i++) g[i] = (g[i] + G[i]) % mod * ntt.inv(2) % mod;
for (int i = m; i < n; i++) g[i] = 0;
}
// given f(x) and g(x), calculate q(x), r(x) such that f(x) = q(x) * g(x) + r(x)
// n = deg(f) + 1, m = deg(g) + 1, deg(q) = n-m, deg(r) < deg(g) - 1 = m
void poly_division(ll f[], ll g[], ll q[], ll r[], const int n, const int m) {
static ll F[maxn], G[maxn], invG[maxn];
for (int i = 0; i <= n-1; i++) F[i] = f[n-1-i];
for (int i = 0; i <= m-1; i++) G[i] = g[m-1-i];
poly_inverse(G, invG, n-m+1);
poly_multiply(F, n-m+1, invG, n-m+1, q);
for (int i = n-m+1; i <= 2LL * (n-m+1); i++) q[i] = 0;
reverse(q, q+n-m+1);
poly_multiply(q, n-m+1, g, m, G);
for (int i = 0; i < m; i++) r[i] = (f[i] - G[i] + mod) % mod;
}
ll f[maxn], g[maxn];
int main() {
int n; cin >> n;
for (int i = 0; i < n; i++) cin >> f[i];
poly_sqrt(f, g, n);
for (int i = 0; i < n; i++) cout << g[i] << " ";
cout << endl;
}
多项式求逆
题意
给定一个多项式 $f(x)$,$deg(f) = n-1$,求多项式 $g(x)$,使得
$$f(x) * g(x) \equiv 1 ~ (\text{mod } x^n)$$
系数对 998244353 取模。
所有的系数均为非负整数,保证有解。
定义 $x^n$:指舍弃含有 $x^n$ 及更高次数的项。
我们设 $g(x)$ 为 $f(x)$ 在 $\text{ mod } x^n$ 意义下的逆元,设 $G(x)$ 为 $f(x)$ 在 $\text{ mod } x^{\lceil{\frac{n}{2}}\rceil}$ 意义下的逆元,则有:
$$f(x)g(x) \equiv 1 (\text{mod } x^{\lceil{\frac{n}{2}}\rceil}), ~~ f(x)G(x) \equiv 1 (\text{mod } x^{\lceil{\frac{n}{2}}\rceil})$$
所以
$$f(x)(g(x) - G(x)) \equiv 0 (\text{mod } x^{\lceil{\frac{n}{2}}\rceil})$$
由于 $deg(f) = n-1$,所以 $f \neq 0 (\text{mod } x^{\lceil{\frac{n}{2}}\rceil})$,所以
$$g(x) - G(x) \equiv 0 (\text{mod } x^{\lceil{\frac{n}{2}}\rceil})$$
两边同时平方,可得
$$g(x)^2 + G(x)^2 - 2g(x)G(x) \equiv 0 (\text{mod } x^n)$$
由于 $f(x)g(x) \equiv 1 (\text{mod } x^n)$,两边同乘以 $f(x)$ 可得:
$$g(x) + f(x)G(x)^2 - 2G(x) \equiv 0 (\text{mod } x^n)$$
所以
$$g(x) \equiv 2G(x) - f(x)G(x)^2 (\text{mod } x^n)$$
注意点
-
$G(x)$ 是 $(\text{mod } x^{\lceil{\frac{n}{2}}\rceil})$ 意义下的逆元,刚好是一个递归的问题,只要求出来 $G(x)$ 即可求出 $g(x)$,而这个式子用 NTT 解决即可。
-
只需要用 DFT 求出 $f(x), G(x)$ 在特殊点的值 $f(x_i), G(x_i)$,然后直接进行上述计算 $2G(x_i) - f(x_i)G(x_i)^2$,然后再 IDFT 回来即可。
-
板子里面使用的 $m$ 代表 $m = deg(f) + 1$,这样是为了递归 base case 的正确处理。
-
如果 $f(x)$ 的常数项 $f(0) = 0$ 则无法求逆。
多项式求 $\ln$
题意
给定一个多项式 $f(x)$,$deg(f) = n-1$,求多项式 $g(x)$,使得
$$g(x) \equiv \ln f(x) ~ (\text{mod } x^n)$$
系数对 998244353 取模。
所有的系数均为非负整数,保证有解。
两边同时求导,可以得到 $$g’(x) \equiv \frac{f’(x)}{f(x)} ~ (\text{mod } x^n)$$
多项式求导和积分都很简单,所以右边可以很容易的计算出来。
计算出来右边以后,两边同时积分即可得到 $g(x)$。
多项式求 $exp$
题意
给定一个多项式 $f(x)$,$deg(f) = n-1$,求多项式 $g(x)$,使得
$$g(x) \equiv e^{f(x)} ~ (\text{mod } x^n)$$
系数对 998244353 取模。
所有的系数均为非负整数,保证 $f_0 = 0$。
前置知识:牛顿迭代法求零点
牛顿迭代法可以快速求出一个函数 $f(x)$ 的零点。
思想:随便找一个 $x_1$ 作为起点,求出 $(x_1, f(x_1))$ 处的切线方程,设 $x_2$ 为这个切线与 $x$ 轴的交点,继续此过程。
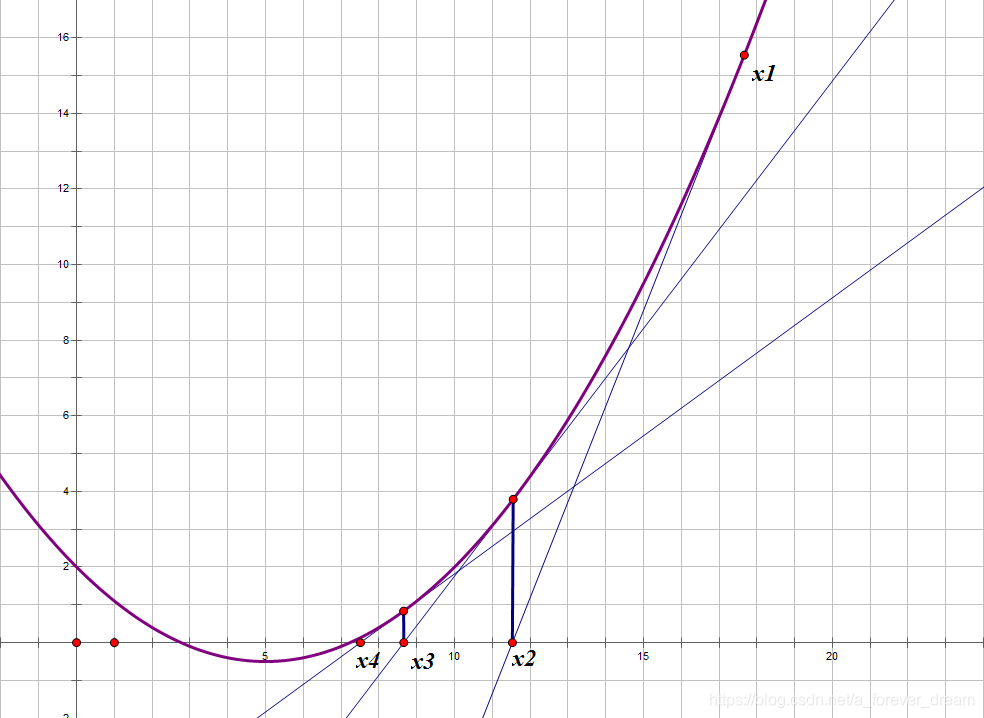
推导:
$f(x)$ 在 $x_1$ 处的切线为
$$y = f’(x_1)(x-x_1) + f(x_1)$$
令 $y = 0$,得到
$$x = x_1 - \frac{f(x_1)}{f’(x_1)}$$
上述的过程对于多项式也适用!
假设我们给定一个多项式 $F(x)$,要求一个多项式 $G(x)$ 使得 $$F(G(x)) \equiv 0 ~ (\text{mod } x^n)$$
则我们可以先求出 $G_1(x)$,满足
$$F(G_1(x)) \equiv 0 ~ (\text{mod } x^{\lceil \frac{n}{2} \rceil})$$
然后根据牛顿迭代的式子,求出
$$G(x) = G_1(x) - \frac{F(G_1(x))}{F’(G_1(x))}$$
令 $G_2(x) = G(x)$,然后递归此过程直到 $n=1$ 即可。
• base case 为 $n = 1$,所以总复杂度为 $O(n \log n)$
证明?需要用到泰勒展开(数学浓度有一点点高所以我先鸽了)
用牛顿迭代求多项式的exp
回顾一下问题:
给定一个多项式 $f(x)$,$deg(f) = n-1$,求多项式 $g(x)$,使得
$$g(x) \equiv e^{f(x)} ~ (\text{mod } x^n)$$
两边同时求 $\ln$,可得:
$$\ln (g(x)) - f(x) \equiv 0 ~ (\text{mod } x^n)$$
设
$$F(g(x)) = \ln (g(x)) - f(x)$$
则我们要求的是 $F(x)$ 在 $(\text{mod } x^n)$ 意义下的零点(注意这个零点本身是个多项式)。
所以根据牛顿迭代的式子,可以写出:
$$g_2(x) = g_1(x) - \frac{F(g_1(x))}{F’(g_1(x))}$$
注意到 $F’(g(x)) = \frac{1}{g(x)}$,所以有:
$$g_2(x) = g_1(x)(1-\ln (g_1(x)) - f(x))$$
• 其中 base case 是 $n=1$ 时,由于 $f_0 = 0$,所以
$$g_0(x) = e^{f_0(x)} = e^0 = 1$$
时间复杂度:$T(n) = T(\frac{n}{2}) + O(n \log n)$,所以 $T(n) = O(n \log n)$
多项式除法
题意
给定一个多项式 $f(x)$ 和一个多项式 $g(x)$,$deg(f) = n, deg(g) = m, n > m$,求 $q(x), r(x)$ 使得:
$$deg(q) = n-m, deg(r) < m$$
$$f(x) = q(x) * g(x) + r(x)$$
系数对 998244353 取模。所有的系数均为非负整数。
设
$$F(x) = x^nf(\frac{1}{x})$$
可以发现 $F(x)$ 就是 $f(x)$ 所有系数翻转过来 得到的多项式。
然后有:
$$f(x) = q(x) * g(x) + r(x)$$
$$f(\frac{1}{x}) = q(\frac{1}{x}) * g(\frac{1}{x}) + r(\frac{1}{x})$$
两边同乘 $x^n$ 可得:
$$x^nf(\frac{1}{x}) = x^{n-m}q(\frac{1}{x}) * x^mg(\frac{1}{x}) + x^{n-m+1} * x^{m-1}r(\frac{1}{x})$$
$$F(x) = Q(x) * G(x) + x^{n-m+1}R(x)$$
两边同时 $\text{mod } x^{n-m+1}$ 可得:
$$F(x) \equiv Q(x) * G(x) ~ (\text{mod } x^{n-m+1})$$
所以
$$Q(x) \equiv \frac{F(x)}{G(x)} ~ (\text{mod } x^{n-m+1})$$
发现 $deg(q) = n-m$,所以刚好求出来的 $Q(x)$ 在 $\text{mod } x^{n-m+1}$ 意义下,就是正确的结果。
所以可以直接计算出 $Q(x)$,翻转系数得到 $q(x)$。
至于 $r(x)$,直接由 $$r(x) = f(x) - q(x) * g(x)$$ 即可得到。
多项式开根
题意
给定一个多项式 $f(x)$,$deg(f) = n-1$,求 $g(x)$ 使得:
$$g^2(x) \equiv f(x) ~ (\text{mod } x^{n})$$
系数对 998244353 取模。保证 $f_0 = 1$,所有的系数均为非负整数。
设
$$F(g(x)) = g^2(x) - f(x)$$
要求的就是 $F(x)$ 的零点。
假设我们已经求出了在 $(\text{mod } x^{\lceil \frac{n}{2}} \rceil)$ 意义下的 $g_1(x)$ 使得 $g_1^2(x) \equiv f(x) (\text{mod } x^{\lceil \frac{n}{2}} \rceil)$
则根据牛顿迭代,有:
$$g_2(x) = g_1(x) - \frac{F(g_1(x))}{F’(g_1(x))}$$
$$= g_1(x) - \frac{g_1^2(x) - f(x)}{2g_1(x)}$$
• base case 为 $n=1$ 时,由于 $f_0 = 1$,直接开根得到 $g_0 = \sqrt 1 = 1$
• 如果 $f_0 \neq 1$,需要 二次剩余 来求出 $g_0$
注:有另外一种不用牛顿迭代的推导方法,可以看 这里
多项式快速幂
题意
给定一个多项式 $f(x)$,和一个正整数 $k$,$deg(f) = n-1$,求 $g(x)$ 使得:
$$g(x) \equiv f(x)^k ~ (\text{mod } x^{n})$$
系数对 998244353 取模。保证 $f_0 = 1$,所有的系数均为非负整数。
两边取 $ln$,可得:
$$\ln g(x) \equiv k \ln f(x)$$
所以计算出 $k \ln f(x)$ 之后,再两边同时取多项式 exp 即可。
注意事项
- 在代码中,使用
ntt.ntt()时注意指定的长度是 $n$,而 不是 $deg(f) = m$ - TODO: 所有需要递归的非递归写法?
- TODO: 二次剩余
