CCPC2020秦皇岛

直接枚举可能出现的最高分，我们知道要保证 $x$ 为最高分，必须有 $x \geq \max \{a_i\}$。

如果我们从小到大枚举 $x$，会发现 $[x * \frac{P}{100}, x]$ 是一个滑动的窗口。

所以本题只要先把所有的 $a_i, b_i$ 放在一起，然后 sort 一下，从 $\max \{a_i\}$ 开始枚举 $x$，在窗口滑动的过程中，利用类似于莫队的思想维护及格人数即可。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+7;

ll n,p,ans = 0;
struct Point {
    ll x, id;
} arr[maxn*2];

int cnt[maxn];
ll cur = 0;

void add(int x) {
    cnt[x]++;
    if (cnt[x] == 1) cur++;
}

void minu(int x) {
    cnt[x]--;
    if (!cnt[x]) cur--;
}

int main() {
    int T; read(T);
    for (int t = 1; t <= T; t++) {
        ans = 0;
        read(n), read(p);
        cur = 0;

        ll lmax = 0;
        for (int i = 1; i <= n; i++) {
            ll a,b; read(b); read(a);
            a *= 100LL, b *= 100LL;
            lmax = max(lmax, a);
            arr[i*2 - 1] = {a, i}, arr[i*2] = {b, i};
        }
        sort(arr+1, arr+2*n+1, [](auto a, auto b) {
            return a.x < b.x;
        });

        int st = 0;
        for (int i = 1; i <= 2*n; i++) {
            if (arr[i].x >= lmax) {
                st = i;
                break;
            }
        }

        int lptr = 0, rptr = 0;
        for (int i = st; i <= 2*n; i++) {
            ll L = arr[i].x / 100 * p, R = arr[i].x;
            while (rptr + 1 <= 2*n && arr[rptr+1].x <= R) {
                rptr++;
                add(arr[rptr].id);
            }
            while (lptr + 1 <= rptr && arr[lptr+1].x < L) {
                lptr++;
                minu(arr[lptr].id);
            }
            ans = max(ans, cur);
        }
        printf("Case #%d: %lld\n", t, ans);
        fill(cnt, cnt+n+5, 0);
    }
}

猜想 $1$：

任意时刻，只有一个飞船是 有用的。

要么我们动这个飞船，要么我们动 $1$ 里面的无限个飞船。如果我们在访问某个子树时没有使用这个飞船，那么这个飞船就再也不会被用到了。

这个猜想是正确的（然而我也不确定怎么严格证明）。

猜想 $2$：

我们可以利用贪心，从 $1$ 开始 dfs，根据 最大深度 的顺序，从小到大 dfs 它的 child。

这个贪心也是正确的，感性理解的话可以考虑最简单的情况：

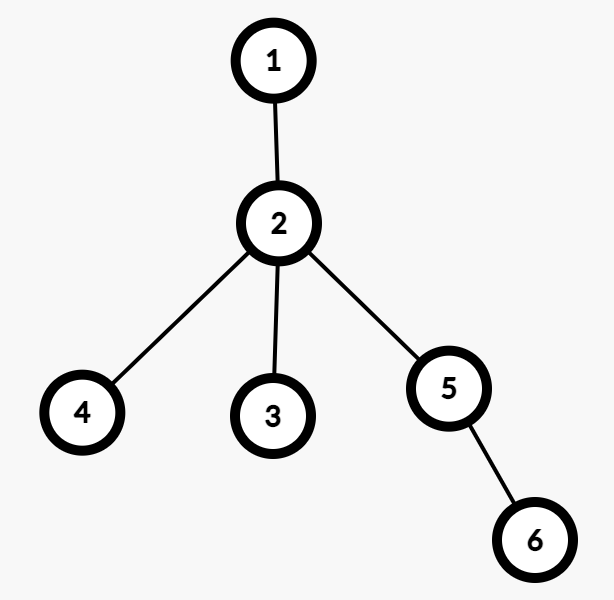
这里从 $2$ 出发的话应该是先访问 $3,4$ ，最后访问 $5$。

利用以上贪心就可以写出一个 $O(n\log n)$ 的解法：

直接维护当前 有用 飞船的位置 $x$，然后每次要移动到下一个点 $y$ 的时候，比较一下 $d(x,y)$ 和 $d(1,y)$ 的距离即可，然后更新 $x=y$。

比赛的时候就是这样写的，然后愉快的T了。

$O(n)$ 正解：

我们发现，对于一个节点 $u$，我们定义 $dp[u]$ 为：访问完 $u$ 的整个子树，并且飞船不回来（即停留在访问时的哪个节点）所需要的步数。

$dp[u]$ 怎么转移？

对于 $u$ 的每个child $v$，除了最后一个访问的 $v$ 以外，其他的 child 都需要访问结束以后，再回到 $u$。

回到 $u$ 的飞船，要么是访问完 $v$ 的那个飞船再走回来，要么我们直接从 $1$ 派一个飞船到 $u$，看哪个距离更近就好了。

所以有：

$$dp[u] = \sum\limits_v \{1 + dp[v] + \min \{maxdep[v] - dep[u], dep[u]\} \}$$

注意到这个转移把 最后一个child $v$ 需要回到 $u$ 的贡献也算上了，且我们知道最后一个child $v$ 访问完毕时，停留的节点深度为 $maxdep[u]$，所以我们需要减掉这个贡献：

$$dp[u] = dp[u] - \min \{maxdep[u] - dep[u], dep[u]\}$$

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+3;

int T, n;
int dep[maxn], maxdep[maxn], head[maxn], ecnt = 1;
ll dp[maxn];
struct Edge {
    int to, nxt;
} edges[maxn];
void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

void dfs1(int u) {
    maxdep[u] = dep[u];
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        dep[to] = dep[u] + 1;
        dfs1(to);
        maxdep[u] = max(maxdep[u], maxdep[to]);
    }
}

void dfs2(int u) {
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        dfs2(to);
        dp[u] += (dp[to] + min(maxdep[to] - dep[u], dep[u]) + 1);
    }
    dp[u] -= (min(maxdep[u] - dep[u], dep[u]));
}

int main() {
    read(T);
    for (int t = 1; t <= T; t++) {
        read(n);
        for (int u = 2; u <= n; u++) {
            int v; read(v);
            addEdge(v, u);
        }

        dep[1] = 0;
        dfs1(1);
        dfs2(1);

        printf("Case #%d: %lld\n",t, dp[1]);
        fill(maxdep, maxdep+n+2, 0);
        fill(dp, dp+n+2, 0);
        ecnt = 1;
        fill(head, head+n+2, 0);
    }

}

获得一个跳跃能力以后，我们每次移动就多了一种移动方式。

注意到我们当前坐标为多少不会影响答案，因为这个获得的跳跃能力，相当于在一个 整数域 中维护一些向量组成的 $span$。每次都看作是从 $(0,0)$ 出发就好了。

现在问题就在于如何维护向量集合了。

有一个结论：

如果集合中有 $\geq 2$ 个不共线向量，则可以用 $(d,0), (x_2,y_2)$ 来表示这个向量集合的 $span$，其中 $d \leq x_2$。

证明？我也不会。

现在考虑一下如果我们加入了一个新的向量 $(x,y)$，怎么更新这些向量？

在整数域下，就需要保证 $d$ 尽量小，而 $y_2$ 也尽量小。

所以我们可以先用 $(x_2,y_2)$ 与 $(x,y)$ 构造出一个 $(x’,0)$ 的向量，然后更新 $d = \gcd(d,x’)$。

要令 $y_2$ 尽量小，则我们用 $(x_2,y_2)$ 与 $(x,y)$ 构造出 $(x’', \gcd(y_2,y))$。

这个构造的过程，就是一个 linear combination 的过程。

那么怎么构造呢？注意到是在整数域下，所以用 $exgcd$！

所以设：

$$ay_2 + by = 0$$

令 $g = \gcd(y_2,y)$，就有：

$$a\frac{y_2}{g} + b\frac{y}{g} = 0$$

所以 $a = -\frac{y}{g}, b = \frac{y_2}{g}$，就有：

$$a(x_2,y_2) + b(x,y) = (x’, 0)$$

然后同理，解出

$$a(x_2,y_2) + b(x,y) = (x’', \gcd(y_2,y))$$

解出来以后，令 $x_2 = x’', y_2 = \gcd(y_2,y)$ 即可。

• 注意需要单独处理 $d,x,y=0$ 的情况。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+3;

int T, Q;
ll curx, cury;
ll exgcd(ll a, ll b, ll& x, ll& y) {
    if (!b) {
        x = 1, y = 0;
        return a;
    }
    ll g = exgcd(b, a%b, x, y);
    ll x2 = x, y2 = y;
    x = y2, y = x2 - a/b * y2;
    return g;
}

ll gcd(ll a, ll b) {
    if (!b) return a;
    return gcd(b, a%b);
}

int cnt = 0;
ll d = 0, x2, y2;

int main() {
    read(T);
    for (int tt = 1; tt <= T; tt++) {
        read(Q);
        d = x2 = y2 = 0;
        ll ans = 0;
        while (Q--) {
            int t; ll x,y,w;
            read(t);
            read(x); read(y);

            if (t == 1) {
                if (y == 0) {
                    d = gcd(d, x);
                    continue;
                }
                ll a,b;
                ll g = exgcd(y, y2, a, b);  // 因为 y2 = 0 无所谓，所以 g != 0
                ll xx = abs(-y2 * x + y * x2) / g;
                d = gcd(d, xx);

                y2 = g;
                x2 = a * x + b * x2;

                if (d)
                    x2 = (x2 % d + d) % d;
            } else {
                read(w);
                if (y == 0) {
                    if (!d && !x) ans += w;
                    if (d > 0 && x % d == 0) ans += w;
                } else {
                    if (y2 && y % y2 == 0) {
                        ll c = y / y2;
                        x -= c * x2;
                        if (d && x % d == 0) ans += w;
                        if (!d && !x) ans += w;
                    }
                }
            }
        }
        printf("Case #%d: %lld\n", tt, ans);
    }
}