单调栈/队列
Contents
单调栈介绍
单调栈可以在 $O(n)$ 时间内解决 “对于每一个index,求右侧/左侧第一个对应数字比它大/小的index” 的问题。
例1 Leetcode2281 Sum of Total Strength of Wizards
题意
给定一个包含 $n$ 个正整数的数组。现在求所有连续的 subarray 的权重和。
一个 subarray 的权重和的定义:这个subarray中的 最小值 乘上 subarray 的和。
其中,$n \leq 10^5, a_i \in [1, 10^9]$,答案对 $10^9+7$ 取模。
题解
首先考虑每一个元素能作为哪些subarray的最小值,很明显这是一个单调栈问题,寻找每个元素左/右的第一个比它小的值。
然而这样可能会产生重复,如 [2,2,2,2] 可能会有问题。
一个常见的套路是 一边开,一边闭。
即:我们对于每个index $i$,找它右侧的第一个 $\leq a_i$ 的index,再找它左侧的第一个 $< a_i$ 的index,这样就解决了重复问题。
对于一个index $i$,我们假设它影响到的区间为 $[L,R]$,那么我们只要找这个区间内,所有 包含了 $i$ 的subarray的和即可。
这样的和怎么找?考虑左边和右边的贡献。
我们将 $[L, i-1]$ 定义为左边,$[i, R]$ 定义为右边。
我们求出前缀和数组 $s[]$,再求出前缀和数组的前缀和 $pre[]$,令:
$$lsum = \sum\limits_{l=L}^{i-1} sum(a[l, i-1]) = \sum\limits_{l=L}^{i-1} (s[i-1] - s[l-1]) = (i-L)*s[i] - \sum\limits_{l=L-1}^{i-2}s[l] = (i-L)*s[i] - (pre[i-2] - pre[L-1])$$
$$rsum = \sum\limits_{r=i}^R sum(a[r, R]) = -(R-i+1)*s[i-1] + (pre[R] - pre[i-1])$$
最后,这个sum就为
$$sum = lsum * rlen + rsum * llen$$
其中 $llen = length[L, i-1] = i-L, rlen = R-i+1$。
代码
class Solution {
public:
#define ll long long
#define maxn 100005
const int mod = (int)(1e9+7);
ll a[maxn];
ll sum[maxn], pre[maxn];
int l[maxn], r[maxn];
ll get_presum(int l, int r) {
if (r < 0 || l > r) return 0;
if (l > 0) return (pre[r] - pre[l-1] + mod) % mod;
return pre[r];
}
int totalStrength(vector<int>& arr) {
int n = arr.size();
ll ans = 0;
for (int i = 1; i <= n; i++) a[i] = arr[i-1];
for (int i = 1; i <= n; i++) sum[i] = (sum[i-1] + a[i]) % mod;
for (int i = 1; i <= n; i++) pre[i] = (pre[i-1] + sum[i]) % mod;
stack<int> st;
fill(r, r+maxn, n+1);
for (int i = 1; i <= n; i++) {
while (st.size() && a[st.top()] >= a[i]) {
r[st.top()] = i;
st.pop();
}
st.push(i);
}
while (st.size()) st.pop();
for (int i = n; i >= 1; i--) {
while (st.size() && a[st.top()] > a[i]) {
l[st.top()] = i;
st.pop();
}
st.push(i);
}
for (int i = 1; i <= n; i++) {
ll L = l[i] + 1, R = r[i] - 1;
// Case1: lsum * rlen
ll res = 0;
ll lsum = ((i - L) * sum[i-1] - get_presum(L-1, i-2) + mod) % mod;
ll rlen = R - i + 1;
res += lsum * rlen % mod;
// Case2: rsum * llen
ll rsum = (-(R - i + 1) * sum[i-1] + get_presum(i, R) + mod) % mod;
ll llen = i - L + 1;
res += rsum * llen % mod;
res %= mod;
ans = (ans + res * a[i] % mod) % mod;
ans %= mod;
}
return ans;
}
};
例2. Serval的数学课堂
题意
定义一个可重集合 $S$ 的 exavg 为:
$$\text{exavg }(S) = \frac{(\sum\limits_{x\in S} x) - \max S - \min S}{|S| - 2}$$
也就是去掉最大最小值后,取平均值。
• exavg 仅对大小至少为 $3$ 的集合有定义。
给定一个整数序列 $A_1, …, A_n$,求所有子区间 $[L,R]$ 的 exavg 的平均值,形式化的,求:
$$\text{avg } \{\text{exavg }(A[L…R]) ~|~ 1 \leq L < R \leq n, R-L+1 \geq 3\}$$
其中,$3 \leq n \leq 5 \times 10^5, A_i \in [0, 998244353)$,答案对 $998244353$ 取模。
题解
经典老套路之:讨论每个数的贡献。
很明显我们只要求 $\text{exavg }$ 的 sum 就行。
贡献可以分为三部分,一个是正常贡献,一个是要减去的最大值,还有一个是要减去的最小值。
对于正常贡献,假设当前这个数为 $a_i$,我们希望知道有哪些区间穿过了 $a_i$,假设一个区间的长度为 $l$,那么我们要求的是
$$\sum\limits_{l} \frac{1}{l-2}$$
其中,区间必须穿过 $a_i$,并且长度 $l \geq 3$。
怎么求呢?
我们令 $C_i$ 为一个长度为 $i$ 的区间内,所有子区间的长度 $l$ 的 $\frac{1}{l-2}$ 的值的和,形式化的:
$$C_i = \sum\limits_{L,R \in [1,i], R-L+1 \geq 3}\frac{1}{(R-L+1)-2}$$
那么就有
$$C_1 = C_2 = 0$$
$$C_i = 2C_{i-1} - C_{i-2} + \frac{1}{i-2}, \forall i \geq 3$$
那么要求所有穿过 $a_i$ 的区间的 $\frac{1}{l-2}$ 之和,假设 $a_i$ 的贡献影响范围是 $[L,R]$,那么有:
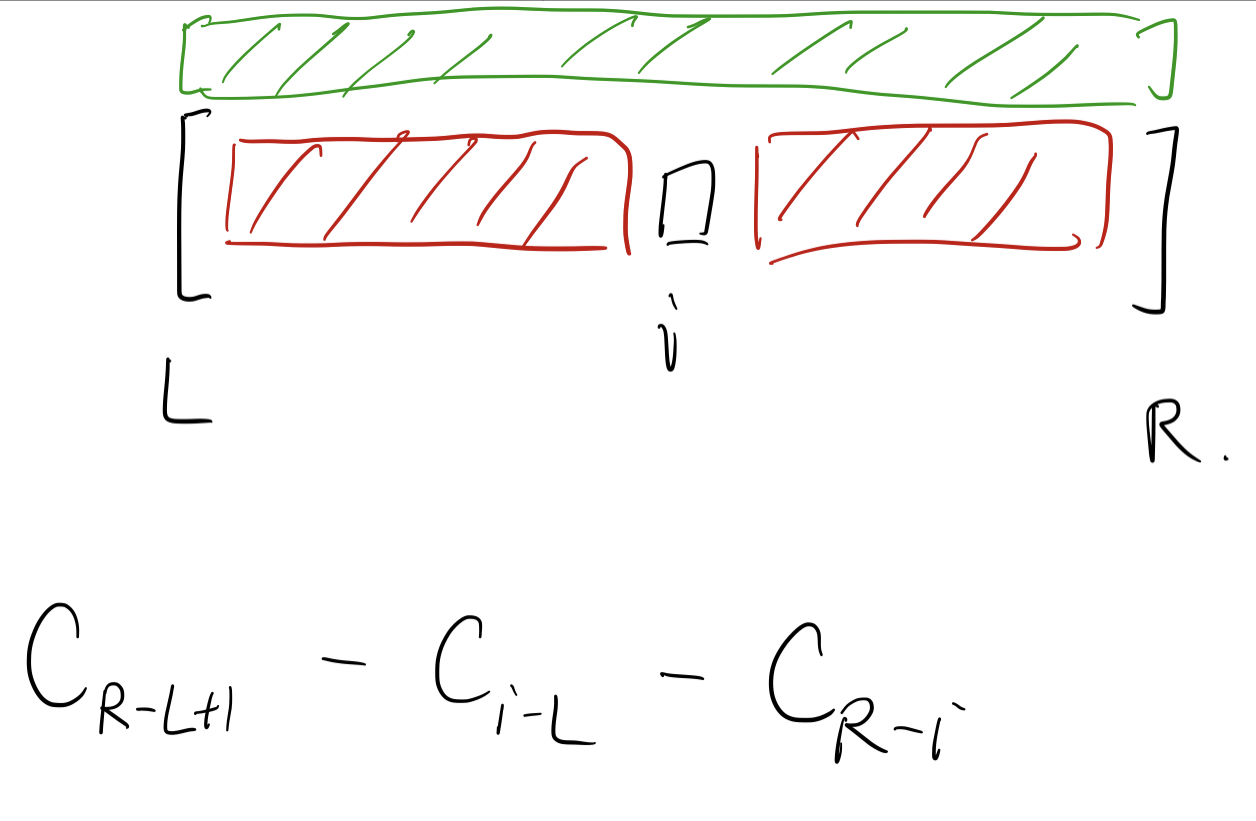
也就是
$$\sum\limits_{l} \frac{1}{l-2} = C_{R-L+1} - C_{i-L} - C_{R-i}$$
那么对于每一个正常贡献,影响范围就是 $L = 1, R = n$。
对于最大最小值,影响范围用单调栈求出即可。
• 为了防止两个值相同导致的贡献重叠,我们利用 这里 的套路:左闭右开 的单调栈即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5+5;
int n;
Z C[maxn]; // C[i]: 区间内所有长度 x 的区间的 1/(x-2) 的和
int a[maxn];
int l[maxn], r[maxn];
Z ans = 0;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 3; i <= n; i++) {
C[i] = C[i-1] * 2 - C[i-2] + Z(1) / (i-2);
}
// 小于的部分
stack<int> st;
fill(r, r+maxn, n+1);
fill(l, l+maxn, 0);
for (int i = 1; i <= n; i++) {
while (st.size() && a[st.top()] >= a[i]) {
r[st.top()] = i;
st.pop();
}
st.push(i);
}
for (int i = n; i >= 1; i--) {
while (st.size() && a[st.top()] > a[i]) {
l[st.top()] = i;
st.pop();
}
st.push(i);
}
while (st.size()) st.pop();
for (int i = 1; i <= n; i++) {
int L = l[i] + 1, R = r[i] - 1;
ans -= (C[R-L+1] - C[R-i] - C[i-L]) * a[i];
}
fill(r, r+maxn, n+1);
fill(l, l+maxn, 0);
for (int i = 1; i <= n; i++) {
while (st.size() && a[st.top()] <= a[i]) {
r[st.top()] = i;
st.pop();
}
st.push(i);
}
for (int i = n; i >= 1; i--) {
while (st.size() && a[st.top()] < a[i]) {
l[st.top()] = i;
st.pop();
}
st.push(i);
}
while (st.size()) st.pop();
for (int i = 1; i <= n; i++) {
int L = l[i] + 1, R = r[i] - 1;
ans -= (C[R-L+1] - C[R-i] - C[i-L]) * a[i];
}
for (int i = 1; i <= n; i++) {
int L = 1, R = n;
ans += (C[R-L+1] - C[R-i] - C[i-L]) * a[i];
}
Z cnt = 0;
for (int i = 3; i <= n; i++) cnt += n-i+1;
ans /= cnt;
cout << ans << endl;
}
例3 CF1795E. Explosions?
题意
给定一个长度为 $n$ 的正整数数组。
我们可以执行若干次操作,每次操作可以选定一个数,让它 $-1$(不能减到负数),每次操作消耗 $1$ 点法力值。
然后我们会选择一个index $i$,消耗 $a_i$ 点法力值,它会被引爆,对两个邻居造成 $a_i - 1$ 点伤害,然后如果邻居被炸死了(比如 $a_{i-1} \leq a_i-1$),则它会继续引爆,对邻居造成 $a_{i-1}-1$ 点伤害。
最后的引爆过程只能进行一次,并且要保证引爆后所有的数都被炸死。
求最小法力值消耗?
其中,$n \leq 3 \times 10^5, a_i \in [1, 10^6]$。
题解
考虑最后引爆的index $i$。
可以知道,在引爆之前,整个数组应该是长这样:
$[a_1,…,a_i]$ 是严格单调递增,$[a_i,…,a_n]$ 是严格单调递减。
有一个特殊情况,$0,0,0,1,2$ 这种也算“严格”单调递增。
现在就是要求 $f_i$,其中 $f_i$ 表示将 $1…i$ 变成严格单调递增的最小操作次数。
这个可以用单调栈在 $O(n)$ 时间算出所有 $f_i$。
具体操作是我们对于栈内元素维护一个pair,$(a_i, cnt_i)$,其中 $a_i$ 就是元素本身,$cnt_i$ 代表以 $i$ 开始,它往前的严格递减(差值恰好为 $1$)的序列长度。
比如 $(9, 1)$ 代表的就是 $[9]$,$(5,3)$ 代表 $[3,4,5]$。
所以我们就用 dp 和单调栈来模拟这个过程即可,注意一些细节即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5;
int T, n;
ll a[maxn], f[maxn], g[maxn];
vector<pll> st;
ll cal(ll x) {
return x*(x+1)/2;
}
void solve() {
st.clear();
for (int i = 1; i <= n; i++) {
ll cnt = 1;
while (!st.empty() && st.back().first >= a[i] - cnt + 1) {
ll c = st.back().first;
ll d = st.back().second;
st.pop_back();
cnt += d;
if (cnt <= a[i]) {
f[i] += (c - (a[i]-(cnt-d))) * d; // starting with a[i] - cnt
} else {
f[i] += (cal(c) - cal(c-d)); // x + (x-1) + (x-2) + ... cnt = 1时
f[i] -= cal(max(0LL, a[i] - (cnt-d))); // if d = 3, a[i] = 9, cnt = 8, cnt + d = 11, a[i] = 9, only used 1
}
}
st.push_back({a[i], min(a[i], cnt)});
f[i] += f[i-1];
}
}
int main() {
fastio;
cin >> T;
while (T--) {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], f[i] = g[i] = 0;
solve();
for (int i = 1; i <= n; i++) g[i] = f[i], f[i] = 0;
// swap(f, g);
reverse(a+1, a+n+1);
solve();
reverse(f+1, f+n+1);
reverse(a+1, a+n+1);
ll ans = 1e18;
for (int i = 1; i <= n; i++) {
ans = min(ans, f[i] + g[i] + a[i]);
}
cout << ans << "\n";
}
}
单调队列介绍
单调队列可以用于解决滑动窗口最值问题。
简单来说,单调队列内维护的是 index,单调队列要满足两个特性:
q[tail] - q[head] < m,其中 $m$ 是窗口的大小。- 队列中的元素,对应的值单调递减/递增。
要维护第二条的话,就需要在插入一个新的元素时,从队列的尾部不断 pop 掉元素,保证单调性(本质上和单调栈一样)。
例1 洛谷P2627 [USACO11OPEN]Mowing the Lawn G
题意
给定一个包含 $n$ 个正整数的数组,从中选取一些数,使得不存在连续的 $>k$ 个数。
输出选取方案中,可能的最大和。
其中,$n \leq 10^5$
题解
DP。设 $dp[i]$ 为前 $i$ 个数字所能得到的最大答案。
所以我们枚举一下上一个不选的位置 $j$,则有
$$dp[i] = \max_{j=i-k}^i\{dp[j-1]+sum(j+1,i)\}$$
$$=\max_{j=i-k}^i\{dp[j-1]+sum[i] - sum[j]\}$$
由于 $i$ 固定,所以可以把 $sum[i]$ 拿出来,我们只要求
$$\max_{j=i-k}^i\{dp[j-1] - sum[j]\}$$
这个东西只与 $j$ 有关,所以就是一个滑动窗口最小值问题了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
ll q[maxn<<1], a[maxn], sum[maxn], dp[maxn];
int head = 1, tail = 0, n, k;
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i], sum[i] = sum[i-1] + a[i];
for (int i = 1; i <= k; i++) {
dp[i] = sum[i];
while (head <= tail && dp[q[tail]] - sum[q[tail]+1] <= dp[i-1] - sum[i]) tail--;
q[++tail] = i-1;
}
for (int i = k+1; i <= n; i++) {
while (head <= tail && dp[q[tail]] - sum[q[tail]+1] <= dp[i-1] - sum[i]) tail--;
q[++tail] = i-1;
while (q[tail] - q[head] >= k+1) head++;
int j = q[head];
dp[i] = sum[i] + dp[j] - sum[j+1];
}
cout << dp[n] << endl;
}
