最小生成树

介绍

最小生成树就是给定一张边有权值的图，求一个生成树使得边权和最小。

最小生成树有着以下几个性质：

最小生成树不唯一，次小生成树可以通过枚举非树边 $(u,v)$，然后替换最小生成树上 $(u,v)$ 这条链上最大边来实现。
所有的最小生成树中，相同权值的边的数量一定相同。
所有的最小生成树中，对于任意的权值 $w$，如果把所有权值 $\leq w$ 的边单独拿出来，那么构成的图的连通性均相同。

证明：

如果不相同，那么这违背了第一条。因为拥有相同权值的次小生成树一定是通过替换一个相同权值的边实现的。（这一条其实也可以直接通过第三条结论得出）。
如果有两种不同的连通性 $G_1,G_2$，那么必然存在一对点 $(u,v)$ 使得 $(u,v)$ 在 $G_1$ 联通，而在 $G_2$ 中不联通。根据 kruskal，这说明我们可以在 $G_2$ 中想办法将 $(u,v)$ 连在一起（因为这样的边一定存在于 $G_1$ 当中）。这不可能发生，因为所有权值 $\leq w$ 的都被拿出来了。

常用的算法 Prim 和 Kruskal 就不再赘述了。

Prim 的思想主要是维护一个联通块，然后逐渐往这个块上加新的点。

Kruskal 的思想是将所有边按照边权 sort 一下，然后用并查集维护联通性防止环的产生。

其实还有一个比较冷门的算法：Boruvka 算法

Boruvka 算法

Boruvka 算法比较适合处理拥有特殊性质的 完全图。比如给定一种计算两点之间边权的方式，然后求最小生成树之类的。

算法总共有 $O(\log V)$ 轮。

每一轮开始：

对于每一个连通块 $i$，我们都找出它与其他连通块的最小边 $(u_i,v_i,w_i)$。
对于每个联通块 $i$ 对应的最小边 $(u_i,v_i,w_i)$，尝试连接 $u$ 和 $v$，如果连接成功，就将连通块合并。

直到只剩下一个联通块。

一般考察这个算法的时候，主要的难点都在于对于每一个联通块，找到它与其他联通块的最小边。

然后因为每次合并，最坏都可以将连通块数量减半，所以最多只有 $O(\log V)$ 轮。

例1 洛谷P2619 [国家集训队]Tree I

题意

给定一个 $n$ 个节点，$m$ 条边的无向联通带权图，每条边是黑色或者白色。

给定非负整数 $k$，求一个刚好包含 $k$ 条白色边的最小生成树权值。

其中，$n \leq 5 \times 10^4, m \leq 10^5$，所有边权均为在 $[1,100]$ 之间的正整数。

数据保证有解。

题解

wqs二分（虽然我并不知道这是什么神奇的算法）。

这个算法针对的是 恰好选 $K$ 个，然后最大/最小化某些值的问题。

具体证明和相关例题以后再学习。

wqs二分的主要思想是给这些 恰好选 $K$ 个 的物品，每个都加上一定的权值（可正可负），相当于鼓励/打击选取这种物品的行为，加上以后再跑原算法。

然后根据原算法跑出来的结果（选取了多少个），然后用二分调整这个额外权值。

所以对于本题，就是给每个白色边添加一个权值，然后跑最小生成树，如果跑出来的最小生成树拥有 $\geq k$ 条白色边，那么就将额外权值往大的那个方向二分（打击选取白边的行为），否则往小二分（鼓励选取白边）。

那什么时候更新答案呢？

我们应当在最小生成树跑出 $\geq k$ 条白边时更新答案，而不是刚好等于 $k$！

首先，我们不确定这个二分的过程是否会出现：额外权值等于 $x$ 时最小生成树有 $(k-1)$ 条白边，额外权值为 $(x+1)$ 时最小生成树有 $(k+1)$ 条白边的情况。

为什么有可能出现呢？

因为最小生成树有可能不唯一！

不过，既然数据保证了一定有解，我们不妨在所有答案中都尽可能的多选白边，那么对于真正的答案对应的额外权值 $x$，一定可以通过非严格的次小生成树来将一些白边替换成黑边，从而保证恰好选择了 $k$ 个白边。

所以只要在最小生成树跑出 $\geq k$ 条白边时更新答案即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4+5;
const int maxm = 1e5+5;

struct Edge {
    int from, to, nxt, w, c;
    bool operator<(const Edge& other) const {
        if (w == other.w) return c < other.c;
        return w < other.w;
    }
} edges[maxm<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v, int w, int c) {
    Edge e = {u, v, head[u], w, c};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

int n,m,k,par[maxn];
int finds(int u) {
    if (par[u] == u) return u;
    return par[u] = finds(par[u]);
}
bool unions(int u, int v) {
    u = finds(u), v = finds(v);
    if (u == v) return 0;
    par[v] = u;
    return 1;
}

Edge tmp[maxm<<1];
int ans = 1e9;
// return true if cnt >= k
bool kruskal(int delta) {
    for (int i = 1; i <= n; i++) par[i] = i;
    for (int i = 1; i < ecnt; i++) {
        tmp[i] = edges[i];
        if (tmp[i].c == 0) tmp[i].w += delta;
    }
    sort(tmp+1, tmp+ecnt);
    int res = 0, cnt = 0, allcnt = 0;
    for (int i = 1; i < ecnt; i++) {
        int u = tmp[i].from, v = tmp[i].to;
        if (finds(u) == finds(v)) continue;
        unions(u,v);
        res += tmp[i].w;
        if (tmp[i].c == 0) cnt++;
        allcnt++;
        if (allcnt == n-1) break;
    }
    if (cnt >= k) ans = res - k * delta;
    return cnt >= k;
}

int main() {
    fastio;
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++) {
        int u,v,w,c; cin >> u >> v >> w >> c;
        u++; v++;
        addEdge(u,v,w,c); addEdge(v,u,w,c);
    }
    int low = -200, high = 200;
    while (high - low >= 10) {
        int mid = (low + high) / 2;
        if (kruskal(mid)) {
            low = mid+1;
        } else {
            high = mid-1;
        }
    }
    for (int mid = low; mid <= high; mid++) kruskal(mid);
    cout << ans << endl;
}

例2 CF888G Xor-MST

题意

给定 $n$ 个节点的无向完全图。每个点有点权 $a_i$。

连接 $i,j$ 节点的边权为 $a_i \text{ xor } a_j$。

求这个图的最小生成树权值。

其中，$n \leq 2 \times 10^5, a_i \in [0,2^{30})$。

法一 Boruvka算法

Boruvka 算法。

为什么它可做呢？因为它的合并操作只有 $O(\log n)$ 轮。

而每一轮操作需要找所有联通块向其他联通块连边的最小边。

如果我们正在处理联通块 $i$，那么要找这个最小边，实际上只要维护一个 01-Trie 来包含所有的点权，然后：

先将联通块 $i$ 内的所有元素从 01-Trie 中删除。
然后对于联通块内的每一个元素 $a_j$，都找 01-Trie 内 XOR 起来最小的那个元素。
这说明这个联通块的最小边找到了，我们再把块内所有元素插入回 01-Trie（保证这个 01-Trie 里面维护的始终是所有的点权）。

找到所有联通块 $i$ 对应的最小边以后，开始连边操作。这样，一轮就结束了。

时间复杂度 $O(n \log n \log 2^{30})$，虽然有点慢，但是可过。

不过这题有个问题，如果有的点权值重复了怎么办？

因为我们在 01-Trie 中寻找到的是一个 XOR 起来最小的点权，但这个点权对应的点可能不唯一。

思考后可以发现，我们先把所有相同的点权全都连起来就好了，毕竟它们之间的边权为 $0$，一定是在最小生成树里的。

然后所有点权相同的点一定在一个联通块内了，我们用一个 map 把一个点权 map 到它们之中的任意一个点即可。

法一代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;

const int M = 31;
struct Node {
    int cnt;
    int child[2];
} trie[maxn * (M+1)];
int id = 1;
void insert(int x) {
    int c = 1;
    for (int i = M; i >= 0; i--) {
        int k = ((x & (1LL<<i)) ? 1 : 0);
        if (!trie[c].child[k]) trie[c].child[k] = ++id;
        c = trie[c].child[k];
        trie[c].cnt++;
    }
}

void erase(int x) {
    int c = 1;
    for (int i = M; i >= 0; i--) {
        int k = ((x & (1LL<<i)) ? 1 : 0);
        c = trie[c].child[k];
        trie[c].cnt--;
    }
}

// query the minimum xor inside the tree
int query(int x) {
    int res = 0, c = 1;
    for (int i = M; i >= 0; i--) {
        int k = ((x & (1LL<<i)) ? 1 : 0);
        if (trie[trie[c].child[k]].cnt == 0) {
            res |= (1LL<<i);
            c = trie[c].child[k^1];
        } else {
            c = trie[c].child[k];
        }
    }
    return res;
}

bool root[maxn];  // is root
int par[maxn];
int n, a[maxn];
vector<int> child[maxn];  // children of root x in dsu
int finds(int u) {
    if (par[u] == u) return u;
    return par[u] = finds(par[u]);
}

void unions(int u, int v) {
    u = finds(u);
    v = finds(v);
    if (u == v) return;
    if (child[u].size() < child[v].size()) swap(u,v);
    par[v] = u;
    root[v] = 0;
    while (child[v].size()) {
        int r = child[v].back(); child[v].pop_back();
        child[u].push_back(r);
    }
}

map<int,int> mp;
ll minval[maxn];
pii link[maxn];  // 用于储存对应的最小边
void boruvka() {
    int cnt = 0;
    for (int i = 1; i <= n; i++)
        if (root[i]) cnt++;

    ll ans = 0;
    while (cnt > 1) {
        for (int i = 1; i <= n; i++) {
            minval[i] = -1;
            link[i] = {-1,-1};
            if (root[i]) {
                for (int u : child[i]) erase(a[u]);
                minval[i] = 4e9;
                for (int u : child[i]) {
                    int res = query(a[u]);
                    if (res < minval[i]) {
                        minval[i] = res;
                        int v = mp[res ^ a[u]];
                        link[i] = {u, v};
                    }
                }
                for (int u : child[i]) insert(a[u]);
            }
        }
        for (int i = 1; i <= n; i++) {
            if (root[i]) {
                int u = link[i].first, v = link[i].second;
                if (finds(u) != finds(v)) {
                    ans += (a[u] ^ a[v]);
                    unions(u, v);
                    cnt--;
                }
            }
        }
    }
    cout << ans << endl;
}

int main() {
    cin >> n;

    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a+1, a+n+1);
    for (int i = 1; i <= n; i++) {
        par[i] = i;
        root[i] = 1;
        child[i].push_back(i);
        mp[a[i]] = i;
        insert(a[i]);
    }
    for (int i = 2; i <= n; i++) {
        if (a[i] == a[i-1]) unions(i, i-1);
    }
    boruvka();
}

法二 01-Trie 子树合并

另外一种做法更加优雅，并且它充分利用了 01-Trie 的特点。

首先我们把所有的 $a_i$ 插入进 01-Trie，看一下 01-Trie 的结构：

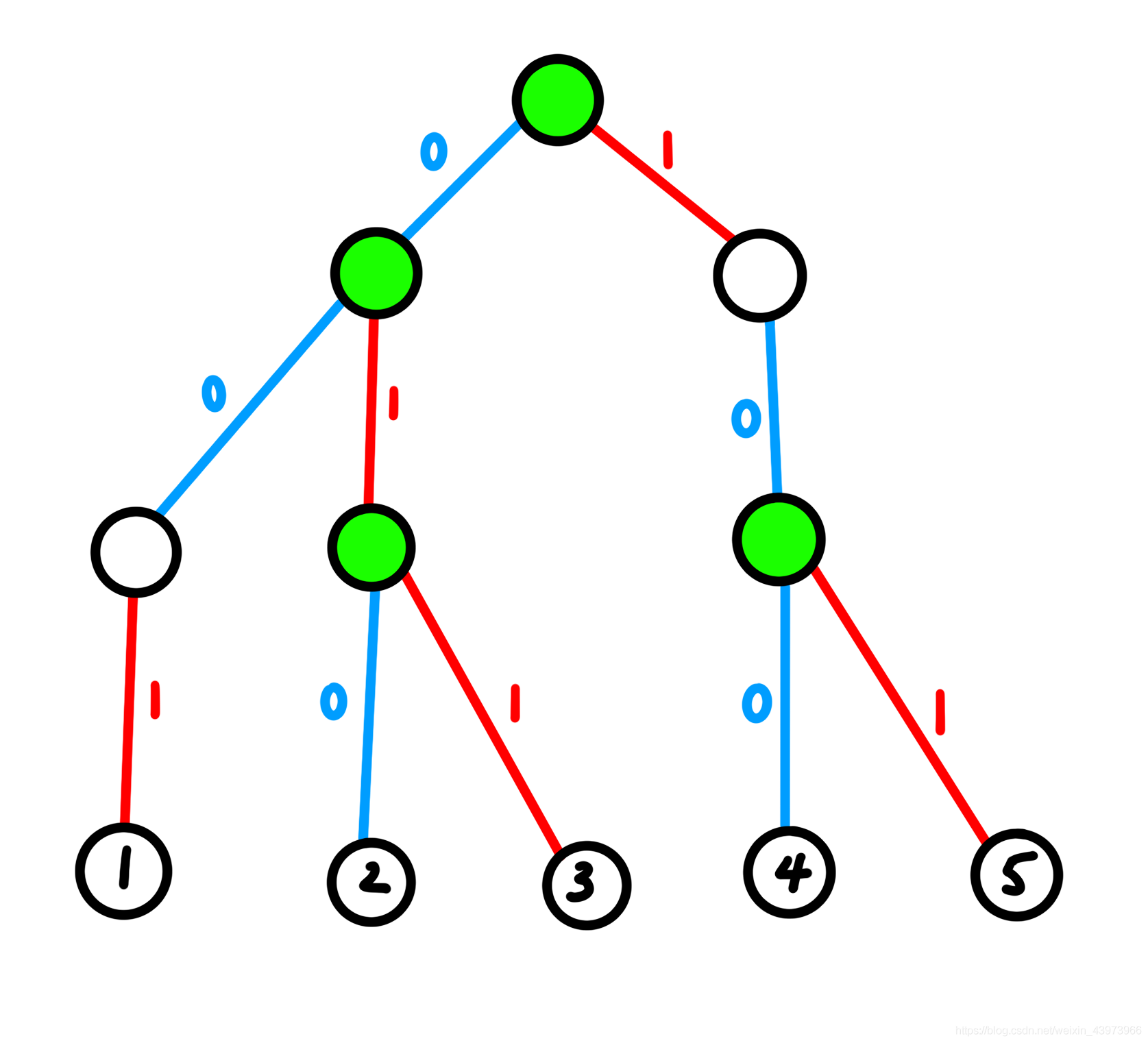
然后我们有几个性质：

每个叶子节点都是原数组里的 $a_i$。
拥有 $2$ 个 child 的节点恰好有 $(n-1)$ 个。
两个数字 $a_u,a_v$ 若位于两个叶子节点 $u,v$，设 $x=LCA(u,v)$，那么它们 XOR 起来的值可以忽略掉 $x$ 上面的部分，只用考虑 $x$ 子树内的部分即可。设 $x$ 所在的高度（叶子的高度为 $0$）为 $m$，则 $a_u \text{ xor } a_v$ 对答案的贡献至少为 (1<<m)。

这些性质说明了什么？首先拥有 $2$ 个 child 的节点恰好有 $(n-1)$ 个，我们可以发现构建一棵最小生成树所需的合并次数刚好也是 $(n-1)$ 次，所以我们每次加入一条边进入MST的过程其实就是这样的 child 合并左右两个子树的过程。

并且因为深度越深的节点带来的贡献越小，所以我们应该先合并深度较深的节点。

那么找到这些节点的话，其实只要在 01-Trie 上跑一个 DFS 即可。

当我们到节点 $x$ 的时候，有三种情况：

只有左child，那么就接着 DFS 左child。
只有右child，那么就接着 DFS 右child。
有左右child，那么就 DFS 左child 和右child，然后给答案加上 (1<<m)，最后加上 $a_u \text{ xor } a_v$ 的最小值，其中 $u$ 在左子树内，$v$ 在右子树内。

最后剩下的问题就在于，如何求：

$a_u \text{ xor } a_v$ 的最小值，其中 $u$ 在左子树内，$v$ 在右子树内？

想想并查集的启发式合并，对于较小的那个子树，我们枚举子树内的每一个元素 $a_u$，然后在较大的那个子树内查询 XOR 值最小的那个元素即可。

那就有两个问题：

如何遍历子树内的每一个元素？
如何在一个子树内查询 XOR 最小值？

回答第一个问题：我们一开始把所有的 $a_i$ sort一下，然后根据 01-Trie 的性质，每个子树就会对应到原数组的一个区间了，就可以得到子树内的元素列表了。

回答第二个问题：和普通查询一样，只不过改一下在 01—Trie 内的起点即可，同时维护一下当前所在的深度。

法二代码

#include <bits/stdc++.h>
using namespace std;

const int maxn = 2e5+5;
const int M = 31;
struct Node {
    int cnt;
    int child[2];
    int L = 1e9, R = -1;
} trie[maxn * (M+1)];
int id = 1;
void insert(int idx, int x) {
    int c = 1;
    for (int i = M; i >= 0; i--) {
        int k = ((x & (1LL<<i)) ? 1 : 0);
        if (!trie[c].child[k]) trie[c].child[k] = ++id;
        c = trie[c].child[k];
        trie[c].cnt++;
        trie[c].L = min(trie[c].L, idx);
        trie[c].R = max(trie[c].R, idx);
    }
}

int query(int c, int x, int m) {
    int res = 0;
    for (int i = m; i >= 0; i--) {
        int k = ((x & (1LL<<i)) ? 1 : 0);
        if (trie[trie[c].child[k]].cnt == 0) {
            res |= (1LL<<i);
            c = trie[c].child[k^1];
        } else {
            c = trie[c].child[k];
        }
    }
    return res;
}

int n, a[maxn];

ll dfs(int c, int m) {
    int lc = trie[c].child[0], rc = trie[c].child[1];
    int lcnt = trie[trie[c].child[0]].cnt, rcnt = trie[trie[c].child[1]].cnt;
    ll ans = 0;
    if (lcnt && rcnt) {
        ans += dfs(lc, m-1);
        ans += dfs(rc, m-1);
        ans += (1LL << m);
        int mn = INT_MAX;
        if (trie[lc].R - trie[lc].L < trie[rc].R - trie[rc].L) {
            for (int nc = trie[lc].L; nc <= trie[lc].R; nc++) {
                mn = min(mn, query(rc, a[nc], m-1));
            }
        } else {
            for (int nc = trie[rc].L; nc <= trie[rc].R; nc++) {
                mn = min(mn, query(lc, a[nc], m-1));
            }
        }
        ans += mn;
    } else if (lcnt) {
        return dfs(lc, m-1);
    } else if (rcnt) {
        return dfs(rc, m-1);
    }
    return ans;
}

int main() {
    fastio;
    cin >> n;

    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a+1, a+n+1);
    for (int i = 1; i <= n; i++) {
        insert(i, a[i]);
    }
    ll ans = dfs(1, M);
    cout << ans << endl;
}

例3 洛谷P4180 [BJWC2010]严格次小生成树

题意

给定一个无向联通图，求其严格次小生成树的权值。

定义严格次小生成树为：一个权值第二小的生成树，且权值严格大于最小生成树的权值。

其中，$n \leq 10^5, m \leq 3 \times 10^5$，边权 $\leq 10^9$，数据保证严格次小生成树一定存在。

题解

次小生成树有两种：

非严格次小生成树（权值不一定严格大于最小生成树）
严格次小生成树

方法都是一样的，先求出最小生成树，然后枚举每一条不在最小生成树上的边 $(u,v)$，然后求最小生成树上 $u,v$ 之间链的最大值，然后把那个边换成这条新的边即可。

树上链的最大值可以用倍增或者树剖。

这种方法只能求出非严格次小生成树。

对于严格次小生成树，只要我们维护链的最大值和次大值（保证次大值严格小于最大值）即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 3e5+5;

struct Edge {
    int from, to, nxt, w;
    bool operator<(const Edge& other) const {
        return w < other.w;
    }
} edges[maxm<<1];
int head[maxn], ecnt = 2, n, m, par[maxn];
void addEdge(int u, int v, int w) {
    Edge e = {u, v, head[u], w};
    head[u] = ecnt;
    edges[ecnt++] = e;
}
bool used[maxm<<1];
int finds(int u) {
    if (par[u] == u) return u;
    return par[u] = finds(par[u]);
}
void unions(int u, int v) {
    u = finds(u), v = finds(v);
    if (u == v) return;
    par[v] = u;
}

struct Node {
    int to;
    int w;
};
vector<Node> adj[maxn];

ll kruskal() {
    for (int i = 1; i <= n; i++) par[i] = i;
    sort(edges+2, edges+ecnt);
    int cnt = 0;
    ll res = 0;
    for (int i = 2; i < ecnt; i++) {
        int u = edges[i].from, v = edges[i].to;
        if (finds(u) == finds(v)) continue;
        unions(u,v);
        used[i] = used[i^1] = 1;
        adj[u].push_back({v, edges[i].w});
        adj[v].push_back({u, edges[i].w});
        res += (ll)edges[i].w;
        cnt++;
        if (cnt == n-1) break;
    }
    return res;
}

int p[maxn][18], dep[maxn];
pii val[maxn][18];

inline void update(pii& p1, pii p2) {
    static int tmp[4];
    tmp[0] = p1.first, tmp[1] = p1.second, tmp[2] = p2.first, tmp[3] = p2.second;
    sort(tmp, tmp+4, greater<int>());
    p1.first = tmp[0];
    for (int i = 1; i < 4; i++) {
        if (tmp[i] != tmp[0]) {
            p1.second = tmp[i];
            break;
        }
    }
}

void dfs(int u, int pa) {
    for (int j = 1; j <= 17; j++) {
        p[u][j] = p[p[u][j-1]][j-1];
        if (p[u][j]) {
            pii p1 = val[u][j-1], p2 = val[p[u][j-1]][j-1];
            update(p1, p2);
            val[u][j] = p1;
        } else {
            val[u][j] = {-1,-1};
        }
    }
    for (Node nd : adj[u]) {
        int v = nd.to, w = nd.w;
        if (v == pa) continue;
        p[v][0] = u;
        val[v][0] = {w, -1};
        dep[v] = dep[u] + 1;
        dfs(v, u);
    }
}


// 查询 u,v 之间的最大值和次大值
pii query(ll u, ll v) {
    pii res = {-1,-1};
    if (dep[u] < dep[v]) swap(u,v);
    int d = dep[u] - dep[v];
    for (int j = 17; j >= 0; j--) {
        if (d & (1<<j)) {
            update(res, val[u][j]);
            u = p[u][j];
        }
    }
    if (u == v) return res;
    for (int j = 17; j >= 0; j--) {
        if (p[u][j] != p[v][j]) {
            update(res, val[u][j]);
            update(res, val[v][j]);
            u = p[u][j], v = p[v][j];
        }
    }
    update(res, val[u][0]);
    update(res, val[v][0]);
    return res;
}

ll solve(ll res) {
    int mn = 1e9+7;
    val[1][0] = {-1,-1};
    dfs(1, 0);
    for (int i = 2; i < ecnt; i++) {
        if (used[i]) continue;
        int w = edges[i].w;
        int u = edges[i].from, v = edges[i].to;
        pii r = query(u,v);
        if (w != r.first) {
            mn = min(mn, w - r.first);
        } else if (w != r.second && r.second >= 0) mn = min(mn, w - r.second);
    }
    return res + mn;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v,w; cin >> u >> v >> w;
        if (u == v) continue;
        addEdge(u,v,w); addEdge(v,u,w);
    }
    ll res = kruskal();
    ll ans = solve(res);
    cout << ans << endl;
}

例4 CF160D Edges in MST

题意

给定一个 $n$ 个节点的无向图，有 $m$ 条带权边。

对于每一条边，都回答它属于以下的哪种情况：

一定在所有 MST（最小生成树）上。
一定在至少一个 MST 上。
不可能在任何 MST 上。

其中，$n \leq 10^5, m \in [n-1, \min(10^5, \frac{n(n-1)}{2})]$。

数据保证无自环和重边。

题解

先求出一棵 MST。

然后对于每个非树边 $(u,v,w)$，要么为 $2$，要么为 $3$。

那么和非严格次小生成树的求法一样，只要求一下 $(u,v)$ 在树上的路径中，最大的权值是否等于 $w$ 即可。如果等于就是 $2$，否则是 $3$。

对于每个树边，要么为 $1$，要么为 $2$。

那么其实只要判断是否存在一条非树边，能够将它替换掉即可。

所以在处理每个非树边 $(u,v,w)$ 时，把 $(u,v)$ 在树上的这条路径全部赋最小值 $w$，全部非树边处理完毕后，查看一下这个树边被覆盖的最小值是多少，如果等于树边的权值就是 $2$，否则就一定大于这个权值，所以是 $1$。

那么路径上的询问，还有赋值，都可以用树剖解决，注意一下维护的是链而不是点，所以要特别处理一下 $LCA(u,v)$。

注意点

一开始求 MST 的时候不需要建双向边，因为整个边的数组被 sort 了，所以后面处理一个边是否是树边的时候会比较麻烦。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 1e5+5;

int n,m,head[maxn],ecnt = 2, pa[maxn];
struct Edge {
    int from, to, nxt, w, id;
    bool operator<(const Edge& other) const {
        return w < other.w;
    }
} edges[maxm];
bool used[maxm];

void addEdge(int u, int v, int w, int id) {
    Edge e = {u, v, head[u], w, id};
    head[u] = ecnt;
    edges[ecnt++] = e;
}
int finds(int u) {
    if (pa[u] == u) return u;
    return pa[u] = finds(pa[u]);
}
void unions(int u, int v) {
    u = finds(u), v = finds(v);
    if (u == v) return;
    pa[v] = u;
}
void kruskal() {
    sort(edges+2, edges+ecnt);
    for (int i = 1; i <= n; i++) pa[i] = i;
    int cnt = 0;
    for (int i = 2; i < ecnt; i++) {
        int u = edges[i].from, v = edges[i].to;
        if (finds(u) == finds(v)) continue;
        int w = edges[i].w;
        unions(u,v);
        used[i] = 1;
        cnt++;
        if (cnt == n-1) break;
    }
}

struct Node {
    int to, w;
};
vector<Node> adj[maxn];

int dep[maxn], par[maxn], sz[maxn], son[maxn], top[maxn], id[maxn], ID, val[maxn], arr[maxn];
void dfs1(int u, int p) {
    dep[u] = dep[p] + 1;
    par[u] = p;
    sz[u] = 1;
    int maxsz = -1;
    for (Node nd : adj[u]) {
        int v = nd.to, w = nd.w;
        if (v == p) continue;
        dfs1(v, u);
        val[v] = w;
        sz[u] += sz[v];
        if (sz[v] > maxsz) {
            son[u] = v;
            maxsz = sz[v];
        }
    }
}

void dfs2(int u, int t) {
    id[u] = ++ID;
    top[u] = t;
    arr[ID] = val[u];
    if (!son[u]) return;
    dfs2(son[u], t);
    for (Node nd : adj[u]) {
        int v = nd.to;
        if (v == par[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}
struct Tree_Node {
    int mn = 1e9+7, w = 1e9+7;
    int lazyw = 1e9+7;
} tr[maxn<<2];
void push_up(int cur) {
    int l = cur<<1, r = l+1;
    tr[cur].mn = max(tr[l].mn, tr[r].mn);
    tr[cur].w = min(tr[l].w, tr[r].w);
}
void push_down(int cur) {
    int l = cur<<1, r = l+1;
    if (tr[cur].lazyw < 1e9) {
        tr[l].lazyw = min(tr[cur].lazyw, tr[l].lazyw);
        tr[l].w = min(tr[cur].lazyw, tr[l].w);
        tr[r].lazyw = min(tr[cur].lazyw, tr[r].lazyw);
        tr[r].w = min(tr[cur].lazyw, tr[r].w);
        tr[cur].lazyw = 1e9+7;
    }
}

void update(int cur, int l, int r, int L, int R, int x) {
    if (L <= l && R >= r) {
        tr[cur].lazyw = min(tr[cur].lazyw, x);
        tr[cur].w = min(tr[cur].w, x);
        return;
    }
    push_down(cur);
    int mid = (l+r) >> 1;
    if (L <= mid) update(cur<<1, l, mid, L, R, x);
    if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
    push_up(cur);
}

// op = 0: query mn  (初始值)
// op = 1: query w  (非树边给的值)
int query(int cur, int l, int r, int L, int R, int op, bool ismax) {
    if (L <= l && R >= r) {
        if (op == 0) return tr[cur].mn;
        if (op == 1) return tr[cur].w;
    }
    push_down(cur);
    int mid = (l+r) >> 1;
    int lres, rres;
    if (ismax) lres = -1, rres = -1;
    else lres = 1e9+7, rres = 1e9+7;
    if (L <= mid) {
        lres = query(cur<<1, l, mid, L, R, op, ismax);
    }
    if (R > mid) {
        rres = query(cur<<1|1, mid+1, r, L, R, op, ismax);
    }
    push_up(cur);
    if (ismax)
        return max(lres, rres);
    else
        return min(lres, rres);
}

void build_tree(int cur, int l, int r) {
    if (l == r) {
        tr[cur].mn = arr[l];
        return;
    }
    int mid = (l+r) >> 1;
    build_tree(cur<<1, l, mid);
    build_tree(cur<<1|1, mid+1, r);
    push_up(cur);
}

void rebuild() {
    for (int i = 2; i < ecnt; i++) {
        if (used[i]) {
            int u = edges[i].from, v = edges[i].to, w = edges[i].w;
            adj[u].push_back({v,w});
            adj[v].push_back({u,w});
        }
    }
    val[1] = 1e9+7;
    dfs1(1, 0);
    dfs2(1, 1);
}

// update the w
void update_path(int u, int v, int x) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        update(1, 1, n, id[top[u]], id[u], x);
        u = par[top[u]];
    }
    if (dep[u] > dep[v]) swap(u,v);
    if (id[u] + 1 <= id[v])
        update(1, 1, n, id[u]+1, id[v], x);
}

int query_path(int u, int v, int op, bool ismax) {
    int res;
    if (ismax) res = -1;
    else res = 1e9+7;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        if (ismax)
            res = max(res, query(1, 1, n, id[top[u]], id[u], op, ismax));
        else
            res = min(res, query(1, 1, n, id[top[u]], id[u], op, ismax));

        u = par[top[u]];
    }
    if (dep[u] > dep[v]) swap(u,v);
    if (id[u] + 1 <= id[v]) {
        if (ismax) 
            res = max(res, query(1, 1, n, id[u]+1, id[v], op, ismax));
        else
            res = min(res, query(1, 1, n, id[u]+1, id[v], op, ismax));
    }
        
    return res;

}

int ans[maxn];
void solve() {
    for (int i = 2; i < ecnt; i++) {
        if (!used[i] && !ans[edges[i].id]) {
            int u = edges[i].from, v = edges[i].to, w = edges[i].w;
            int res = query_path(u,v,0,1);
            if (res == w) {
                ans[edges[i].id] = 2;
            } else ans[edges[i].id] = 3;
            update_path(u,v,w);
        }
    }
    for (int i = 2; i < ecnt; i++) {
        if (used[i] && !ans[edges[i].id]) {
            int u = edges[i].from, v = edges[i].to, w = edges[i].w;
            int res = query_path(u,v,1,0);
            if (res == w) ans[edges[i].id] = 2;
            else ans[edges[i].id] = 1;
        }
    }
}

int main() {
    fastio;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v,w; cin >> u >> v >> w;
        addEdge(u,v,w,i); 
    }
    kruskal();
    rebuild();
    build_tree(1, 1, n);
    solve();
    for (int i = 1; i <= m; i++) {
        if (ans[i] == 1) cout << "any\n";
        if (ans[i] == 2) cout << "at least one\n";
        if (ans[i] == 3) cout << "none\n";
    }
}

例5 CF891C Envy

题意

给定一个 $n$ 个点，$m$ 条边的无向联通图，每个边有边权 $w_i$。

现在给定 $q$ 个询问，每次询问 $k_i$ 条边 $e_1,e_2,…,e_{k_i}$。

对于每个询问，我们需要回答这些边是否能存在于同一个最小生成树当中。

其中，$n,m,q,w_i \leq 5 \times 10^5$。

并且保证所有询问中，询问的边数的总和不超过 $5 \times 10^5$。

题解

由最小生成树的性质第二条和第三条，我们可以发现不同权值的边之间不会互相影响。

所以我们考虑按照权值分开来处理。

换而言之，我们不再按照每个询问来回答，而是把每个询问中的权值相同的边都拿出来分别处理。这样，问题就变成了：

给定一些权值相同（均为 $w$）的边，判断这些边是否能存在于同一个 MST 中？

根据 MST 性质的第三条，我们只需要处理出最小生成树中权值严格小于 $w$ 的边的连通性。然后判断一下这些边在当前联通图下，是否都能够 unions() 即可。处理完当前询问，就用可撤销并查集退回。

所以，我们只要把每个询问中所有权值相同的边都拿出来，然后从小到大开始跑 kruskal，跑的过程中回答当前权值的询问即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5+5;
const int maxm = 5e5+5;

struct Edge {
    int u, v, w;
} edges[maxm], edges_tmp[maxm];
struct Query {
    int id;
    vector<int> vec;
};
struct State {
    int u, v, szu;
};
int par[maxn], sz[maxn];
State st[maxn];
int tail = 0;
int finds(int u) {
    if (par[u] == u) return u;
    return finds(par[u]);
}
void unions(int u, int v) {
    u = finds(u), v = finds(v);
    if (sz[u] < sz[v]) swap(u,v);
    if (u == v) return;
    st[++tail] = {u, v, sz[u]};
    par[v] = u;
    sz[u] += sz[v];
}
void cancel() {
    int u = st[tail].u, v = st[tail].v;
    par[v] = v;
    sz[u] = st[tail].szu;
    tail--;
}

int n, m, q;
bool ans[maxn];
vector<Query> val_query[maxn];  // val_query[i]: 询问权值为 i 的
int main() {
    fastio;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) par[i] = i, sz[i] = 1;
    for (int i = 1; i <= m; i++) {
        cin >> edges[i].u >> edges[i].v >> edges[i].w;
        edges_tmp[i] = edges[i];
    }
    sort(edges_tmp+1, edges_tmp+m+1, [](auto a, auto b) {
        return a.w < b.w;
    });
    cin >> q;
    for (int i = 1; i <= q; i++) {
        int k; cin >> k;
        vector<int> tmp;
        for (int j = 1; j <= k; j++) {
            int e; cin >> e;
            tmp.push_back(e);
        }
        sort(tmp.begin(), tmp.end(), [&](auto a, auto b) {
            return edges[a].w < edges[b].w;
        });
        for (int j = 0; j < k; j++) {
            int e = tmp[j];
            int w = edges[tmp[j]].w;
            if (j == 0 || edges[tmp[j]].w != edges[tmp[j-1]].w) {
                val_query[w].push_back({i, vector<int>()});
            }
            val_query[w].back().vec.push_back(e);
        }
    }
    fill(ans+1, ans+q+1, 1);
    int pt = 0;
    for (int w = 1; w <= 5e5; w++) {
        for (Query que : val_query[w]) {
            int id = que.id;
            int curt = tail;
            for (int e : que.vec) {
                int u = edges[e].u, v = edges[e].v;
                if (finds(u) == finds(v)) {
                    ans[id] = 0;
                    break;
                }
                unions(u,v);
            }
            while (tail != curt) {
                cancel();
            }
        }
        while (pt + 1 <= m && edges_tmp[pt+1].w == w) {
            pt++;
            Edge ce = edges_tmp[pt];
            int u = ce.u, v = ce.v;
            if (finds(u) != finds(v)) unions(u,v);
        }
    }
    for (int i = 1; i <= q; i++) {
        cout << (ans[i] ? "YES" : "NO") << "\n";
    }
}

参考链接

Boruvka算法：https://luckyglass.github.io/2019/19Oct31stArt1/

Contents

介绍

Boruvka 算法

例1 洛谷P2619 [国家集训队]Tree I

例2 CF888G Xor-MST

例3 洛谷P4180 [BJWC2010]严格次小生成树

例4 CF160D Edges in MST

例5 CF891C Envy

参考链接