最短路径树

先说个假做法：对于每个 $i$，求 $\min \{d_u+w(u,i)\}$，其中 $u$ 为 $i$ 的 neighbor 且不为原来最短路使用的那个 $u$。

为什么假了？因为我们没有办法保证 $1\rightarrow u$ 的最短路上有没有经过 $i$，如果经过了，它就有可能用到了不被允许使用的边。

下面说正解。

对于本题，首先就是从 $1$ 开始求一个最短路，然后构建出来最短路径树。

那么 $1$ 节点到 $i$ 节点的最短路就是树上的一条路径。

现在我们只考虑这个最短路径树，如果 $1 \rightarrow i$ 的最后一条边被断开了，那么 $1$ 与 $i$ 就会被分割在两个不同的联通块内。

• 注意到每个联通块也是一棵树，$1$ 和 $i$ 分别是 2 个树的根节点。

这意味着我们需要使用一条非树边将 $1$ 和 $i$ 所在的两个联通块重新链接起来。

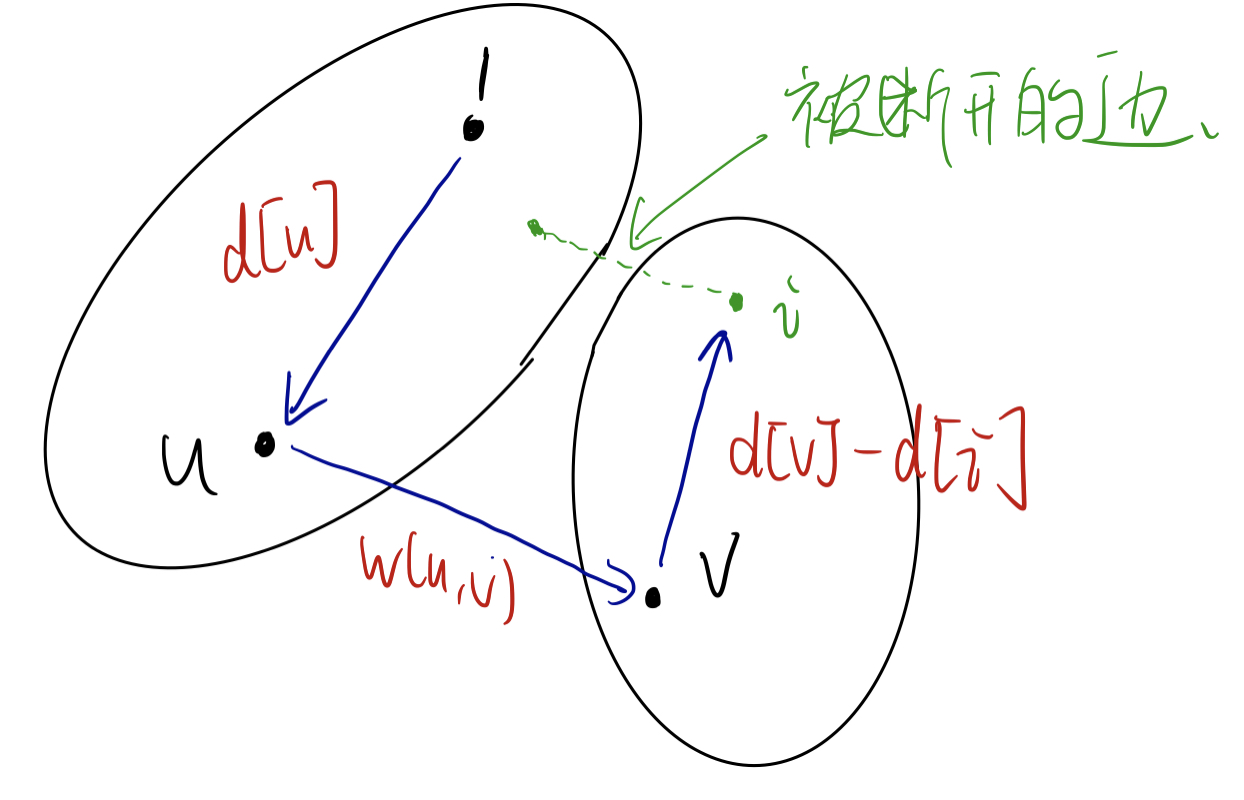
假设这条边是 $(u,v)$，那么新的 $1 \rightarrow i$ 最短路就等于：

$$d[u] + w(u,v) + d[v] - d[i]$$

这里 $d[u]$ 指原先从 $1 \rightarrow u$ 的最短路长度，注意到对于固定的 $i$，这个 $d[i]$ 是个常数。所以我们只关心

$$d[u] + w(u,v) + d[v]$$

我们会发现这个对于每条边 $(u,v)$ 也是个定值。

那么现在我们只需要考虑，有哪些 $(u,v)$ 能对 $i$ 产生这样的贡献就行了。

那么还是老套路，把点的问题转成链的问题，那么一个非树边 $(u,v,w)$ 就相当于把 $d[u] + w(u,v) + d[v]$ 的这个值赋最小值给 $(u,v)$ 路径（指树上路径）上的所有边。

然后每个节点 $i$ 对应的就是 $(i, par[i])$ 这条边。

所以用树剖维护链的更新和查询即可。

• 注：为什么不直接更新点……我也没想明白？尝试了一下似乎会WA。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 2e5+5;

int n,m;
struct Edge {
    int from, to, nxt, w;
} edges[maxm<<1];
int head[maxn], ecnt = 2, d[maxn], pre[maxn];
bool vis[maxn];

void addEdge(int u, int v, int w) {
    Edge e = {u, v, head[u], w};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

struct Node {
    int u, dis;
    bool operator<(const Node& other) const {
        return dis > other.dis;
    }
};
priority_queue<Node> pq;
void dijkstra() {
    pq.push({1,0});
    memset(d, 63, sizeof(d));
    while (!pq.empty()) {
        auto nd = pq.top(); pq.pop();
        int u = nd.u, dis = nd.dis;
        if (vis[u]) continue;
        vis[u] = 1;
        d[u] = dis;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].to, w = edges[e].w;
            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;
                pre[v] = u;
                pq.push({v,d[v]});
            }
        }
    }
}

struct Node2 {
    int to, w;
};
vector<Node2> adj[maxn];
int dep[maxn], par[maxn], sz[maxn], son[maxn], top[maxn], id[maxn], ID, arr[maxn], ans[maxn];

void dfs1(int u, int p) {
    dep[u] = dep[p] + 1;
    par[u] = p;
    sz[u] = 1;
    for (Node2 nd : adj[u]) {
        int to = nd.to;
        if (to == p) continue;
        dfs1(to, u);
        sz[u] += sz[to];
        if (sz[to] > sz[son[u]]) son[u] = to;
    }
}

void dfs2(int u, int t) {
    id[u] = ++ID;
    top[u] = t;
    arr[ID] = 1e9;
    if (!son[u]) return;
    dfs2(son[u], t);
    for (Node2 nd : adj[u]) {
        int to = nd.to;
        if (to == par[u] || to == son[u]) continue;
        dfs2(to, to);
    }
}

struct Tree_Node {
    int mn = 1e9, lazy = 1e9;
} tr[maxn<<2];

void push_up(int cur) {
    tr[cur].mn = min(tr[cur<<1].mn, tr[cur<<1|1].mn);
}

void push_down(int cur) {
    if (tr[cur].lazy == 1e9) return;
    int lazy = tr[cur].lazy;
    tr[cur].lazy = 1e9;
    int l = cur<<1, r = l+1;
    tr[l].lazy = min(tr[l].lazy, lazy);
    tr[l].mn = min(tr[l].mn, lazy);
    tr[r].lazy = min(tr[r].lazy, lazy);
    tr[r].mn = min(tr[r].mn, lazy);
}

void update(int cur, int l, int r, int L, int R, int x) {
    if (L <= l && R >= r) {
        tr[cur].lazy = min(tr[cur].lazy, x);
        tr[cur].mn = min(tr[cur].mn, x);
        return;
    }
    push_down(cur);
    int mid = (l+r) >> 1;
    if (L <= mid) update(cur<<1, l, mid, L, R, x);
    if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
    push_up(cur);
}

int query(int cur, int l, int r, int L, int R) {
    if (L <= l && R >= r) return tr[cur].mn;
    push_down(cur);
    int lres = 1e9, rres = 1e9;
    int mid = (l+r) >> 1;
    if (L <= mid) lres = query(cur<<1, l, mid, L, R);
    if (R > mid) rres = query(cur<<1|1, mid+1, r, L, R);
    push_up(cur);
    return min(lres, rres);
}

void update_path(int u, int v, int x) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        update(1, 1, n, id[top[u]], id[u], x);
        u = par[top[u]];
    }
    if (dep[u] > dep[v]) swap(u,v);
    if (id[u] + 1 <= id[v])
        update(1, 1, n, id[u]+1, id[v], x);
}

int query_path(int u, int v) {
    int res = 1e9;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        res = min(res, query(1, 1, n, id[top[u]], id[u]));
        u = par[top[u]];
    }
    if (dep[u] > dep[v]) swap(u,v);
    if (id[u] + 1 <= id[v])
        res = min(res, query(1, 1, n, id[u]+1, id[v]));
    return res;
}

int LCA(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u,v);
        u = par[top[u]];
    }
    if (dep[u] > dep[v]) swap(u,v);
    return u;
}

void rebuild() {
    for (int i = 2; i <= n; i++) {
        adj[i].push_back({pre[i], d[i] - d[pre[i]]});
        adj[pre[i]].push_back({i, d[i] - d[pre[i]]});
    }
    dfs1(1, 0);
    dfs2(1, 1);
}

void solve() {
    for (int e = 2; e < ecnt; e++) {
        int u = edges[e].from, v = edges[e].to, w = edges[e].w;
        if (pre[u] == v || pre[v] == u) continue;  // 树边
        update_path(u, v, d[v] + w + d[u]);
    }
    for (int u = 2; u <= n; u++) {
        int q = query_path(u, par[u]);
        ans[u] = -d[u] + q;
        cout << (ans[u] > 1e8 ? -1 : ans[u]) << "\n";
    }
}

int main() {
    cin >> n >> m;
    memset(ans, 63, sizeof(ans));
    for (int i = 1; i <= m; i++) {
        int u,v,w; cin >> u >> v >> w;
        addEdge(u,v,w); addEdge(v,u,w);
    }
    dijkstra();
    rebuild();
    solve();
}

看到 $n \leq 1500$，我们想到枚举每一个最短路径的起点 $u$。

也就是从 $1$ 到 $n$，分别为起点，总共跑 $n$ 次 dijkstra。

每次跑一个 dijkstra，我们就可以得到以 $u$ 为起点的最短路径。

这里我们不妨设以 $1$ 为起点。

那么我们可以枚举每一条边，然后判断这条边被经过了多少次。

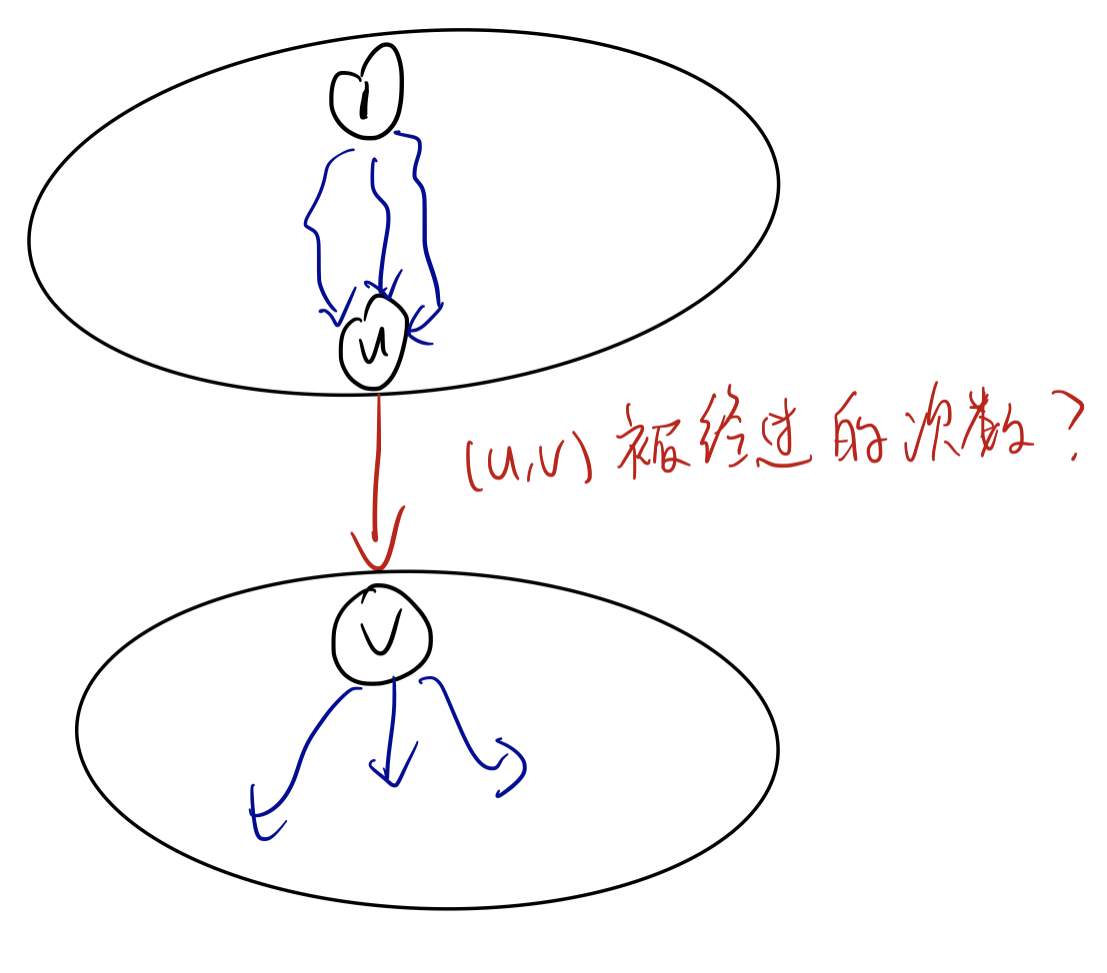
对于一条边 $(u,v)$，它被经过的次数就等于：

所以我们设 $f_x$ 为：$1 \rightarrow x$ 的最短路径条数。

注意到，如果我们构建好 最短路径图（就是将保留所有满足 $dis[v] = dis[u] + w(v,u)$ 的边 $(v,u)$）后，这个最短路径图是一个 DAG。

所以就可以跑 DAG 上的 DP了（用拓扑排序）。

• 注意这个 DAG 是最短路径图！每个节点为起点的 dijkstra 所形成的最短路径图都各不相同！

所以从 $1$ 出发跑拓扑排序（入度为 $0$ 开始），就可以求出 $1 \rightarrow u$ 的最短路径条数。

然后我们再将拓扑序列存下来，用拓扑序列反向跑一次 DP，就可以求出 $\sum (1 \rightarrow x$ 的最短路径条数$)$ （通过拓扑序的反序，将 $v$ 子图内的所有点加到 $v$ 上）。

时间复杂度：每个点开始跑一个 dijkstra，然后跑两次拓扑排序，然后枚举每一个边，所以

$$T(n) = n * (n \log m + 2n + m) = O(n^2\log m)$$

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1505;
const int maxm = 5005;

struct Edge {
    int u, v, nxt, w;
} edges[maxm];
int head[maxn], ecnt = 1, n, m;
void addEdge(int u, int v, int w) {
    Edge e = {u, v, head[u], w};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

struct Node {
    int v, d;
    bool operator<(const Node& other) const {
        return d > other.d;
    }
};
int dis[maxn];
bool vis[maxn];
priority_queue<Node> pq;
ll ans[maxm], dp1[maxn], dp2[maxn];
vector<int> tmp;
int ind[maxn];
void dijkstra(int start) {
    while (pq.size()) pq.pop();
    tmp.clear();
    fill(dis, dis+maxn, 1e9);
    fill(vis, vis+maxn, 0);
    fill(dp1, dp1+maxn, 0);
    fill(dp2, dp2+maxn, 0);
    fill(ind, ind+maxn, 0);
    dis[start] = 0;
    pq.push({start, 0});
    while (!pq.empty()) {
        int u = pq.top().v, d = pq.top().d; pq.pop();
        if (vis[u]) continue;
        vis[u] = 1;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].v, w = edges[e].w;
            if (d + w < dis[v]) {
                dis[v] = d + w;
                pq.push({v, dis[v]});
            }
        }
    }
}

vector<int> topo_seq;
void topo(int start) {
    for (int e = 1; e <= m; e++) {
        int u = edges[e].u, v = edges[e].v, w = edges[e].w;
        if (dis[u] + w == dis[v]) ind[v]++;
    }
    tmp.clear();
    topo_seq.clear();

    tmp.push_back(start);
    topo_seq.push_back(start);
    dp1[start] = 1;
    while (tmp.size()) {
        int u = tmp.back(); tmp.pop_back();
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].v, w = edges[e].w;
            if (dis[v] == dis[u] + w) {
                dp1[v] = (dp1[v] + dp1[u]) % mod;
                ind[v]--;
                if (!ind[v]) tmp.push_back(v), topo_seq.push_back(v);
            }
        }
    }

    // 反向 topo
    reverse(topo_seq.begin(), topo_seq.end());
    for (int u : topo_seq) {
        dp2[u] = 1;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].v, w = edges[e].w;
            if (dis[v] == dis[u] + w) {
                dp2[u] = (dp2[u] + dp2[v]) % mod;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v,w; cin >> u >> v >> w;
        addEdge(u,v,w);
    }
    for (int i = 1; i <= n; i++) {
        dijkstra(i);
        topo(i);
        for (int e = 1; e <= m; e++) {
            int u = edges[e].u, v = edges[e].v, w = edges[e].w;
            if (dis[v] == dis[u] + w) {
                ans[e] = (ans[e] + dp1[u] * dp2[v] % mod) % mod;
            }
        }
    }
    for (int e = 1; e <= m; e++) {
        cout << ans[e] << "\n";
    }
}