曼哈顿距离 和 切比雪夫距离
Contents
曼哈顿距离
定义两个点 $A(x_1,y_1), B(x_2,y_2)$,则 $A,B$ 之间的曼哈顿距离为:
$$d(A,B) = |x_1 - x_2| + |y_1 - y_2|$$
曼哈顿距离的性质:
- 对称性:$d(A,B) = d(B,A)$
- 三角形不等式:$d(A,C) \leq d(A,B) + d(B,C)$
曼哈顿距离的应用场景:
- 单位网格图上,只能往 上下左右 $4$ 个方向走,那么网格图上两点之间的距离为 曼哈顿距离。
- 国际象棋棋盘上,车从一个格子走到另外一个格子就是曼哈顿距离。
距离原点的曼哈顿距离为 $1$ 组成的点:
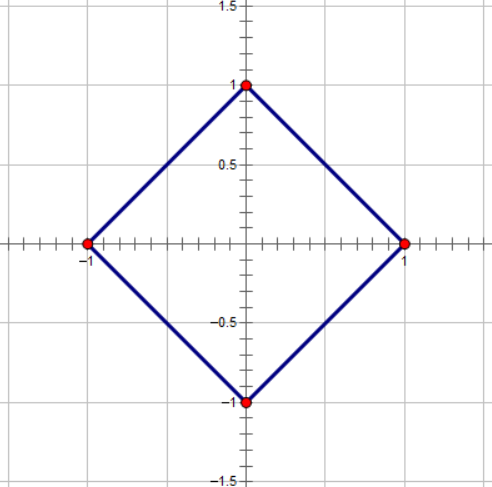
切比雪夫距离
定义两个点 $A(x_1,y_1), B(x_2,y_2)$,则 $A,B$ 之间的切比雪夫距离为:
$$d(A,B) = \max \{|x_1 - x_2|,|y_1 - y_2|\}$$
- 单位网格图上,可以 上下左右,也可以 斜着,共往 $8$ 个方向走,那么网格图上两点之间的距离为 切比雪夫距离。
- 国际象棋棋盘上,王从一个格子走到另外一个格子就是切比雪夫距离。
由于可以互相转化,所以切比雪夫距离也遵循曼哈顿距离的性质。
距离原点的切比雪夫距离为 $1$ 组成的点:
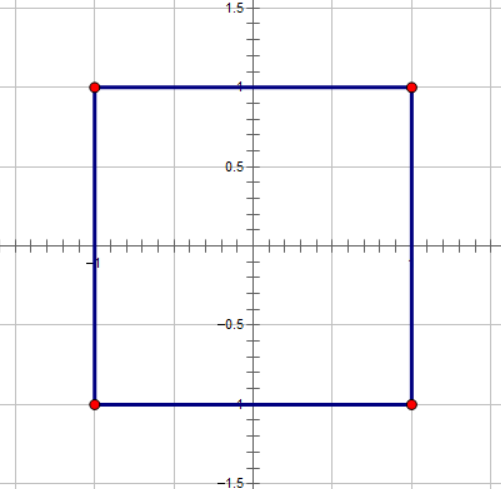
曼哈顿距离 转 切比雪夫距离
对于曼哈顿坐标系中的所有点 $(x,y)$,我们都把它转到切比雪夫坐标系中,得到 $(x+y,x-y)$。
$$(x,y) \rightarrow (x+y,x-y)$$
那么,曼哈顿坐标系中的 曼哈顿距离 等于 切比雪夫坐标系中的 切比雪夫距离。
• 证明:略,大概就是将坐标系中的单位正方形进行转化即可。
切比雪夫距离 转 曼哈顿距离
对于切比雪夫坐标系中的所有点 $(x,y)$,我们都把它转到曼哈顿坐标系中,得到 $(\frac{x+y}{2},\frac{x-y}{2})$。
$$(x,y) \rightarrow (\frac{x+y}{2},\frac{x-y}{2})$$
那么,切比雪夫坐标系中的 切比雪夫距离 等于 曼哈顿坐标系中的 曼哈顿距离。
• 证明:使用上面的逆变换,即可得到答案。
例题
例1 洛谷P2906 [USACO08OPEN]Cow Neighborhoods G
题意
在二维平面上 给定 $n$ 个奶牛的整数坐标 $(x_i,y_i)$,给定正整数 $C$,若满足以下两个条件之一,则我们定义两个奶牛 $i,j$ 为一个群:
- $i,j$ 之间的曼哈顿距离 $\leq C$。
- 存在奶牛 $k$,使得 $i,k$ 和 $k,j$ 为一个群。
求牛群数量,并求出最大的牛群大小。
其中,$n \leq 10^5, C,x_i,x_j \in [1,10^9]$
题解
很明显是并查集,现在我们要观察怎么并。
可以发现,本题主要的难点就在于如何减少并查集合并数量。所以我们在 sort 以后就要想办法如何使用最少的合并次数,达到答案?
首先,我们把曼哈顿距离转为切比雪夫距离。经过变换以后,可得到 $(x_i’,y_i’) = (x_i+y_i,x_i-y_i)$。
然后,我们知道对于两个限制的常用套路是 分开讨论。
我们根据 $x$ 坐标先 sort 一下所有的点,然后从 $1$ 枚举到 $n$。
当我们位于第 $i$ 个点时,我们可以利用滑动窗口知道有哪些点是 $i$ 可以合并到的。(保证 $|x_j - x_i| \leq C$ 即可,其中 $j\in [1,i]$)。
然后在这个滑动窗口内,我们只要找出 $\geq y_i$ 的第一个 $y_{j_1}$ 和 $\leq y_i$ 的第一个 $y_{j_2}$,然后合并 $(i,j_1)$ 和 $(i,j_2)$ 即可。
• 为什么只需要合并这两个元素呢?
证:考虑我们最终合并出来的结果,是一个个联通块。那么对于联通块内的一个 $(x_i,y_i)$,它必然通过上述过程与 $\geq y_i$ 的第一个 $y_{j_1}$ 和 $\leq y_i$ 的第一个 $y_{j_2}$ 所合并了。
最后,我们用 set 来维护这个滑动窗口并且找出 $y_{j_1}$ 和 $y_{j_2}$ 即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n,par[maxn],sz[maxn];
ll c;
struct Node {
int id;
ll x,y;
bool operator<(const Node& other) const {
if (y == other.y) return x < other.x;
return y < other.y;
}
} arr[maxn];
int finds(int u) {
if (par[u] == u) return u;
return par[u] = finds(par[u]);
}
void unions(int u, int v) {
u = finds(u), v = finds(v);
if (u == v) return;
par[v] = u;
}
set<Node> s;
int main() {
fastio;
cin >> n >> c;
for (int i = 1; i <= n; i++) {
int x,y; cin >> x >> y;
arr[i].x = x + y;
arr[i].y = x - y;
}
sort(arr+1, arr+n+1, [](auto a, auto b) { return a.x < b.x; });
for (int i = 1; i <= n; i++) par[i] = i, arr[i].id = i;
int l = 1;
s.insert(arr[1]);
for (int r = 2; r <= n; r++) {
while (arr[r].x - arr[l].x > c) {
s.erase(arr[l]);
l++;
}
// 找第一个 <= y 的
auto p = s.upper_bound({0,0,arr[r].y});
if (p != s.begin()) {
if (abs(prev(p)->y - arr[r].y) <= c)
unions(arr[r].id, prev(p)->id);
}
// 找第一个 >= y 的
p = s.lower_bound({0,0,arr[r].y});
if (p != s.end()) {
if (abs(p->y - arr[r].y) <= c)
unions(arr[r].id, p->id);
}
s.insert(arr[r]);
}
int mx = 0, cnt = 0;
for (int i = 1; i <= n; i++) {
int u = finds(i);
sz[u]++;
}
for (int i = 1; i <= n; i++) {
if (sz[i]) cnt++, mx = max(sz[i], mx);
}
cout << cnt << " " << mx << endl;
}
例2 洛谷P3964 [TJOI2013]松鼠聚会
题意
二维平面上给定 $n$ 个点 $(x_i,y_i)$,每个点到它周围的 $8$ 个点
$$(x−1,y),(x+1,y),(x,y-1),(x,y+1),(x-1,y+1)(x-1,y-1), (x+1,y+1), (x+1,y-1)$$
距离均为 $1$。
求一个点,使得它到其他所有的点的距离和最小,求这个最小和。
题解
这实际上就是切比雪夫距离。
问题变成平面上求一个点,使得它到其他点的切比雪夫距离之和最小。
这个问题不好求,不如转化成曼哈顿距离。
$$(x,y) \rightarrow (\frac{x+y}{2},\frac{x-y}{2})$$
为了防止小数的问题,我们把所有坐标乘上 $2$,最后答案除以 $2$ 即可。
转化以后就变成求一个点,使得它到其他点的曼哈顿距离之和最小。
这就好做了,因为曼哈顿距离的 $x,y$ 坐标贡献是独立的,互不影响。
所以先根据 $x$ 坐标 sort 一下所有点,用前缀和即可得到每个点到其他点曼哈顿距离的 $x$ 坐标上的贡献。
再根据 $y$ 坐标 sort 一下,用前缀和即可得到每个点到其他点曼哈顿距离的 $y$ 坐标上的贡献。
把两个贡献加起来即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n;
struct Node {
int id;
ll x,y;
} arr[maxn];
ll pre[maxn], suf[maxn], sumx[maxn], sumy[maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
ll x,y; cin >> x >> y;
arr[i].x = x + y;
arr[i].y = x - y;
arr[i].id = i;
}
sort(arr+1, arr+n+1, [](auto a, auto b) {
return a.x < b.x;
});
for (int i = 1; i <= n; i++) pre[i] = pre[i-1] + arr[i].x;
for (int i = n; i >= 1; i--) suf[i] = suf[i+1] + arr[i].x;
for (int i = 1; i <= n; i++) {
int id = arr[i].id;
sumx[id] = (ll)(i) * arr[i].x - pre[i] + suf[i] - (ll)(n-i+1) * arr[i].x;
}
sort(arr+1, arr+n+1, [](auto a, auto b) {
return a.y < b.y;
});
for (int i = 1; i <= n; i++) pre[i] = pre[i-1] + arr[i].y;
for (int i = n; i >= 1; i--) suf[i] = suf[i+1] + arr[i].y;
for (int i = 1; i <= n; i++) {
int id = arr[i].id;
sumy[id] = (ll)(i) * arr[i].y - pre[i] + suf[i] - (ll)(n-i+1) * arr[i].y;
}
ll mn = 1e18;
for (int i = 1; i <= n; i++) {
mn = min(mn, sumx[i] + sumy[i]);
}
cout << mn / 2 << endl;
}
例3 洛谷P4648 [IOI2007] pairs 动物对数
题意
给定 $4$ 个正整数,$B,N,D,M$。
在 $B$ 维空间中,有 $N$ 个点,定义两个点之间的距离为他们的曼哈顿距离,并且它们的坐标大小都在 $[1,M]$ 中。
求距离 $\leq D$ 的点对数量?
规定:
$B \in [1,3], N \in [1,10^5], D \in [1, 10^9]$。
当 $B = 1$ 时,$M \leq 7.5 \times 10^8$。
当 $B = 2$ 时,$M \leq 7.5 \times 10^4$。
当 $B = 3$ 时,$M \leq 75$。
题解
$B=1$:
直接 sort 一下,然后滑动窗口即可。
$B=2$:
曼哈顿距离转一下切比雪夫距离,然后老套路,按照 $x$ 坐标 sort 一下,接着从 $1$ 枚举到 $n$。
设我们现在到第 $i$ 个元素了,那么我们就可以维护一个滑动窗口保证窗口内的所有元素 $j$ 都满足 $x_i-x_j \leq D$。
接着我们只需要查询这个窗口内,有多少个元素满足 $y_j \in [x_i-D, x_i+D]$ 即可。
那么这个开一个权值线段树维护一下就行了,值域在 $[1, 1.5 \times 10^5]$。
• 注意一下转切比雪夫距离之后,$y$ 坐标有可能有负数,那么就把所有点的 $y$ 坐标都加上 $M$,这样 $y_i \in [1, 2M]$了。
$B=3$:
老套路,仍然是按照 $x$ 坐标先 sort 一下。
然后我们把点按照 $x$ 坐标分类,所以每个 $x$ 坐标对应的就是一个二维平面。由于 $M \leq 75$,所以这样的二维平面只有 $75$ 个。
然后我们枚举每个点,对于每个点 $i$,都在每一个二维平面 $j$ 上询问一下这个平面上有多少点到它的曼哈顿距离为 $d$,其中
$$d = D - |x_i - x_j|$$
这个询问的过程,完全是一个二维平面上的问题。
我们再将曼哈顿距离转成切比雪夫距离。
注意到,在二维平面上,距离一个点的切比雪夫 $\leq d$ 的点形成的实际上是一个正方形。
所以这就变成了一个查询二维平面上,一个正方形内点的数量有多少了。
于是用二维前缀和就可以 $O(1)$ 查询。
• 最后要记得把答案减去 $n$,因为每个点都会把自己算一次。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int B, n;
ll D, M;
void solve1() {
int a[maxn];
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
sort(a+1, a+n+1);
int l = 1;
ll ans = 0;
for (int r = 1; r <= n; r++) {
while (a[r] - a[l] > D) l++;
ans += (ll)(r-l);
}
cout << ans << endl;
}
int id = 0;
void update(int* sum, int cur, int l, int r, int p, int x) {
sum[cur] += x;
if (l == r) {
return;
}
int mid = (l+r) >> 1;
if (p <= mid) update(sum, cur<<1, l, mid, p, x);
if (p > mid) update(sum, cur<<1|1, mid+1, r, p, x);
}
int query(int* sum, int cur, int l, int r, int L, int R) {
if (L <= l && R >= r) return sum[cur];
int mid = (l+r) >> 1;
int res = 0;
if (L <= mid) res += query(sum, cur<<1, l, mid, L, R);
if (R > mid) res += query(sum, cur<<1|1, mid+1, r, L, R);
return res;
}
void solve2() {
int sum[(M+100)<<3];
memset(sum, 0, sizeof(sum));
pii arr[maxn];
for (int i = 1; i <= n; i++) {
int x,y; cin >> x >> y;
arr[i].first = x + y;
arr[i].second = x - y + M; // 移动 M 格
}
sort(arr+1, arr+n+1);
ll ans = 0;
int l = 1;
for (int r = 1; r <= n; r++) {
while (arr[r].first - arr[l].first > D) {
update(sum, 1, 1, 2 * M, arr[l].second, -1);
l++;
}
ans += (ll)(query(sum, 1, 1, 2 * M, max(1LL, arr[r].second - D), min(2 * M, arr[r].second + D)));
update(sum, 1, 1, 2 * M, arr[r].second, 1);
}
cout << ans << endl;
}
void solve3() {
const int MM = 77;
vector<pii> arr[MM];
int sum[MM][MM*2][MM*2];
memset(sum, 0, sizeof(sum));
for (int i = 1; i <= n; i++) {
int x,y,z; cin >> x >> y >> z;
arr[x].push_back({y+z, y-z+M});
sum[x][y+z][y-z+M]++;
}
ll ans = -n;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= 2 * M; j++) {
for (int k = 1; k <= 2 * M; k++) {
sum[i][j][k] += sum[i][j-1][k] + sum[i][j][k-1] - sum[i][j-1][k-1];
}
}
}
for (int ii = 1; ii <= M; ii++) {
for (pii a : arr[ii]) {
ll x = a.first, y = a.second;
for (int i = 1; i <= M; i++) {
ll d = D - abs(i - ii); // 只考虑 y,z 内的距离
if (d >= 0) {
int x1 = min(2*M, x + d), y1 = min(2*M, y + d);
int x2 = max(1LL, x - d) - 1, y2 = min(2*M, y + d);
int x3 = max(1LL, x - d) - 1, y3 = max(1LL, y - d) - 1;
int x4 = min(2*M, x + d), y4 = max(1LL, y - d) - 1;
ans += (ll)(sum[i][x1][y1] - sum[i][x2][y2] - sum[i][x4][y4] + sum[i][x3][y3]);
}
}
}
}
cout << ans/2 << "\n";
}
int main() {
cin >> B >> n >> D >> M;
if (B == 1) solve1();
if (B == 2) solve2();
if (B == 3) solve3();
}
