最大权闭合子图

定义

闭合子图

对于一个 有向图 $G=(V,E)$，它的一个闭合子图 $G'=(V’,E’)$ 满足：

$\forall u \in V'$，如果 $(u,v) \in E$，则 $v \in V’, (u,v) \in E'$

简单来说，就是对于子图中的每一个点 $u$，它的所有后继（它指向的）节点 $v$ 都在子图中。

最大权闭合子图

如果这个图有点权，那么最大权闭合子图就是一个 最大点权和 的 闭合子图。

算法

最大权闭合子图问题可以利用最小割解决。

结论

建立超级源点 $s$，对于所有点权 $w_u >0$ 的点 $u$，连 $(s,u,w_u)$。
建立超级汇点 $t$，对于所有点权 $w_v < 0$ 的点 $v$，连 $(v,t,|w_v|)$。
对于原图中的所有边 $(u,v)$，都连一条无限大的边 $(u,v,\infty)$。

• 点权为 $0$ 的点不用和 $s,t$ 相连。

那么答案就等于：

最大权闭合子图的权值和 $=$ 所有权值为正的权值和 $-$ 最小割

证明

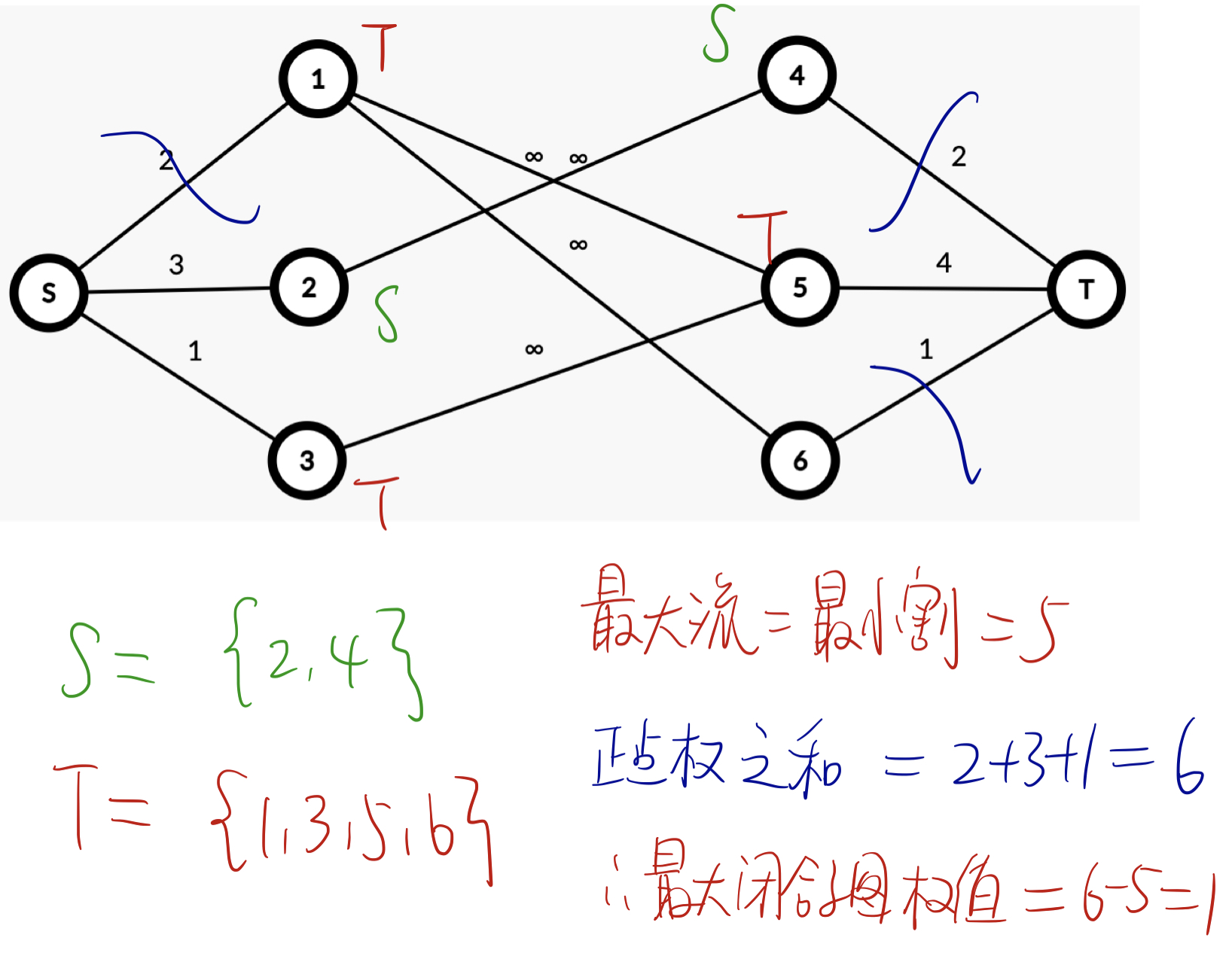
我们有以下 lemma：

结论1：最小割为简单割（容量不为正无穷）

很明显可以通过割与 $s,t$ 相连的边获得最小割，所以最小割不会包括正无穷的边。

结论2：最小割将原图分为 $S,T$ 两个集合（指分别包含 $s,t$ 的两个集合），$S$ 集合是一个闭合子图。

由于最小割不包含正无穷的边，$S$ 内不存在连向集合 $T$ 的边，所以 $S$ 内所有的出边都指向 $S$ 内部，满足闭合图定义。

结论3：$S$ 集合是所求的最大权闭合子图。

（不会证明）

结论4：最大权闭合子图的权值和 $=$ 所有权值为正的权值和 $-$ 最小割

我们定义 $a_S$ 分别为 $S$ 内所有正权值之和，$b_S$ 为 $S$ 内所有负权值之和的绝对值，形式化的：

$$a_S = \sum\limits_{u\in S, w_u>0}w_u, b_S = |\sum\limits_{u\in S, w_u<0}w_u|$$

则，$S$ 的权值（最大权闭合子图的权值）$W_S$ 就等于：

$$W_S = a_S - b_S$$

再定义最小割 $C$ 为一个边集的权值集合 $C = \{w_{C_1},w_{C_2},…\}$，并且定义 $a_C$ 为 $C$ 内所有正权值之和，$b_C$ 为 $C$ 内所有负权值之和的绝对值。

则最小割的值 $W_C$等于：

$$W_C = a_C + b_C$$

因为 $S$ 内所有拥有负权值的节点，必然指向 $t$，且由于 $S$ 是闭合子图，所以最小割中，所有负边必然都来自于 $S$ 内的负权值节点。

所以 $b_S = b_C$。

同理，$a_S$ 与 $a_C$ 互补，即 $a_S + a_C = a_G$，其中 $a_G$ 代表原图中所有正权值之和。

所以：

$$W_S + W_C = a_G$$

可得：

$$W_S = a_G - W_C$$

例题

例1 洛谷P4174 [NOI2006] 最大获利

题意

有一共 $n$ 个中转站，$m$ 个用户。

建立第 $i$ 个中转站所需的成本为 $P_i$。

每个用户的信息为 $A_i,B_i,C_i$，代表这个用户将会使用中转站 $A_i$ 和 $B_i$ 进行通讯，并且可以带来 $C_i$ 的利润。

求最大净利润（利润减去成本）？

其中，$n \leq 5000, m \leq 50000$。

题解

对于这种 满足某种条件才能获得利润，而这些条件 需要一定成本才能满足 的题，就可以考虑最大权闭合子图。

把每个中转站看作一个节点，然后这些节点向汇点 $t$ 连边，容量为 $P_i$。

把每个用户（获利条件）看作一个节点，比如一个条件 $(A_i,B_i,C_i)$ 就看作一个节点 $x_i$。

然后连 $(s,x_i,C_i)$ 代表选择这个节点可以获得 $C_i$ 的利润，再连 $(x_i,A_i,\infty), (x_i,B_i,\infty)$ 代表如果要获得这个利润，则必须建立中转站 $A_i,B_i$。

求出最大权闭合子图的权值即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 55005;
const int maxm = 1e6+55005+10;

int n,m,s,t;
int head[maxn], ecnt = 2, cur[maxn];  // ecnt 从 2 开始，方便取反向边
struct Edge {
    int to, nxt;
    ll w;
} edges[maxm<<1];

void addEdge(int u, int v, ll w) {
    Edge e = {v, head[u], w};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

int dis[maxn];
bool bfs() {
    queue<int> q;
    memset(dis, -1, sizeof(dis));
    memcpy(cur, head, sizeof(head));
    dis[s] = 0;
    q.push(s);
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int e = head[u]; e; e = edges[e].nxt) {
            int to = edges[e].to;
            ll w = edges[e].w;
            if (dis[to] >= 0 || w == 0) continue;  // visited 或者 edge 已经不存在
            dis[to] = dis[u] + 1;
            q.push(to);
            if (to == t) return 1;  // 仍然存在增广路，直接返回
        }
    }
    return 0;
}

ll dfs(int u, ll in) {
    if (u == t) return in;  // 如果已经运到了终点，直接返回入量
    ll out = 0;
    for (int e = cur[u]; e; e = edges[e].nxt) {
        cur[u] = e;
        int to = edges[e].to;
        ll w = edges[e].w;
        if (dis[to] != dis[u] + 1 || w == 0) continue;  // 不是下一层 或者 edge已经不存在

        // 否则，可以往外运输流量
        ll res = dfs(to, min(in, w));
        in -= res;
        out += res;
        edges[e].w -= res;
        edges[e^1].w += res;

        if (in == 0) break;  // 如果已经没有可以向外流的了，直接 break
    }
    if (out == 0) dis[u] = -1;  // 说明当前节点已经不能向外运输流量了，忽略不计
    return out;
}

void add(int u, int v, ll w) {
    addEdge(u, v, w);
    addEdge(v, u, 0);
}

ll maxflow() {
    ll ans = 0;
    while (bfs()) {
        ans += dfs(s, 1e18);
    }
    return ans;
}

int val[maxn];
int main() {
    cin >> n >> m;
    s = 55001, t = 55002;
    for (int i = 1; i <= n; i++) {
        int p; cin >> p;
        add(i, t, p);
    }
    int sum = 0;
    for (int i = 1; i <= m; i++) {
        int u,v; ll w;
        cin >> u >> v >> w;
        add(i+n, u, 1e9);
        add(i+n, v, 1e9);
        add(s, i+n, w);
        sum += w;
    }
    int res = maxflow();
    cout << sum - res << endl;
}

例2 CCPC2021威海 H city safety

题意

给定一个 $n$ 个节点的树。对于每个节点 $i$，初始状态下没有加固。加固节点 $i$ 的代价为 $w_i$。

对于每一个节点，如果距离它 $\leq j$ 的所有节点均被加固了，则它会提供额外 $v_j$ 的收益。

求加固方案，使得净收益最大？

其中，$n \leq 200, v_j \leq v_{j+1}$。

最小割题解

最大权闭合子图。

拆点，对于每个节点 $u$，我们把它拆成 $u,u_0,u_1,u_2,…,u_{n-1}$。

其中 $u_j$ 代表对于节点 $u$，距离它 $\leq j$ 的所有节点均被加固了。

我们知道 $u_j$ 就代表一种收益，那么这个收益有什么条件呢？

如果要选 $u_j$，则我们必须选择 $u_{j-1}$，这样我们就保证了选择 $u_j$ 也会选择到所有距离 $\leq (j-1)$ 的点。
如果选了 $u_j$，我们必须选择距离 $u$ 恰好为 $j$ 的点。

所以连边的方案就是：

连 $(s,u_j,v_j-v_{j-1})$：代表选择了 $u_j$ 这个收益，注意到选择 $u_j$ 后默认选择了 $u_{j-1}$，所以我们只需要给这个点赋值一个增量 $v_j-v_{j-1}$ 即可。
连 $(u_j,u_{j-1},\infty)$
连 $(u_j,v,\infty)$：代表我们需要选择距离 $u$ 距离 $u$ 恰好为 $j$ 的点 $v$。
对于每一个 $v \in [1,n]$，连 $(v,t,w_v)$：代表需要付出 $w_v$ 的代价来加固点 $v$。

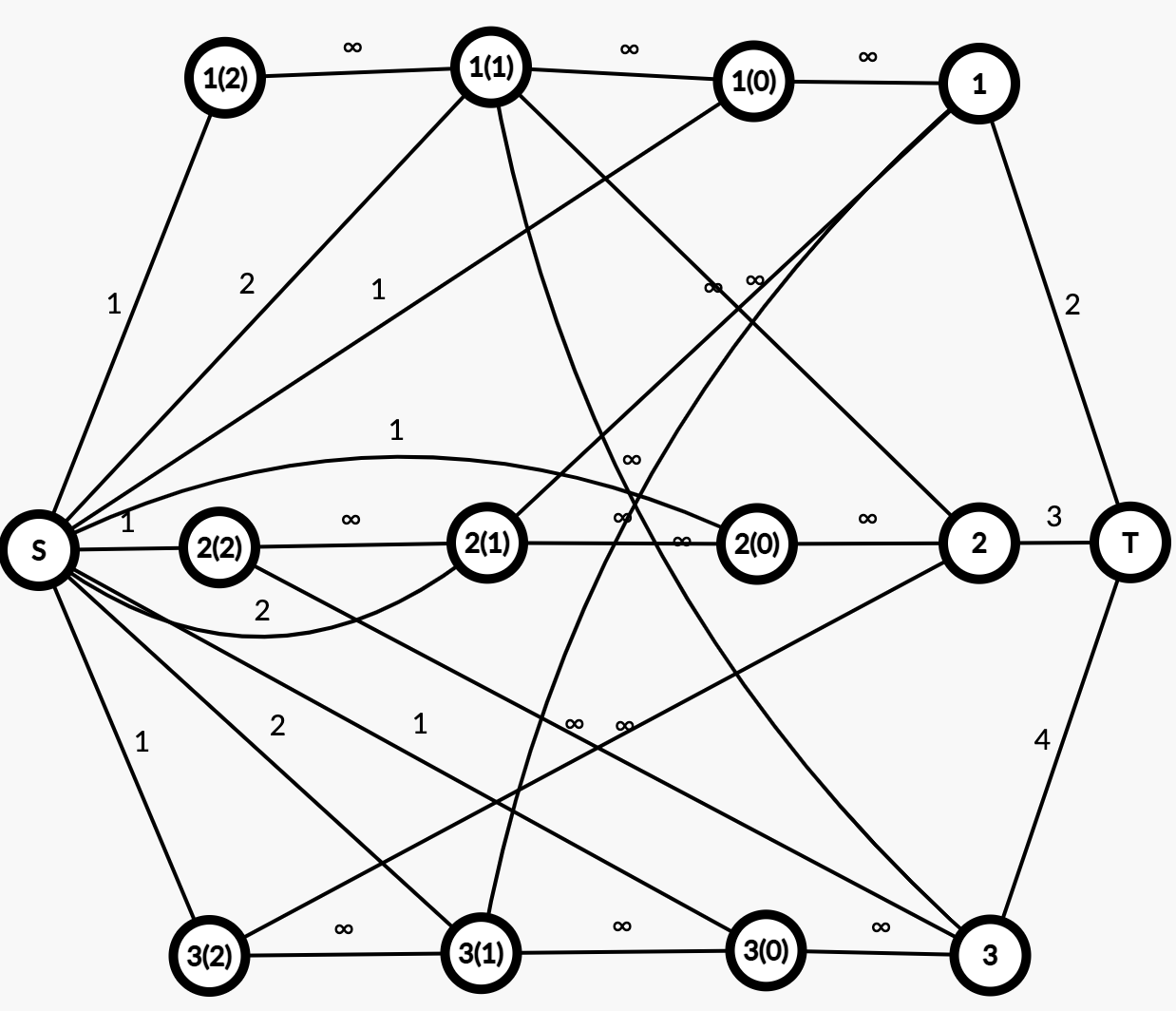
比如对于样例：$n=3, E = \{(1,2),(1,3)\}$，且 $v_0=1, v_1=3, v_2=4, w_1 = 2,w_2=3,w_3=4$，则建的图如下：

最小割代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 210;
const int maxm = 8e5+5;

int n,m,s,t;
int head[maxn*maxn], ecnt = 2, cur[maxn*maxn];  // ecnt 从 2 开始，方便取反向边
struct Edge {
    int to, nxt;
    ll w;
} edges[maxm<<1];

void addEdge(int u, int v, ll w) {
    Edge e = {v, head[u], w};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

int dis[maxn*maxn];
bool bfs() {
    queue<int> q;
    memset(dis, -1, sizeof(dis));
    memcpy(cur, head, sizeof(head));
    dis[s] = 0;
    q.push(s);
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int e = head[u]; e; e = edges[e].nxt) {
            int to = edges[e].to;
            ll w = edges[e].w;
            if (dis[to] >= 0 || w == 0) continue;  // visited 或者 edge 已经不存在
            dis[to] = dis[u] + 1;
            q.push(to);
            if (to == t) return 1;  // 仍然存在增广路，直接返回
        }
    }
    return 0;
}

ll dfs(int u, ll in) {
    if (u == t) return in;  // 如果已经运到了终点，直接返回入量
    ll out = 0;
    for (int e = cur[u]; e; e = edges[e].nxt) {
        cur[u] = e;
        int to = edges[e].to;
        ll w = edges[e].w;
        if (dis[to] != dis[u] + 1 || w == 0) continue;  // 不是下一层 或者 edge已经不存在

        // 否则，可以往外运输流量
        ll res = dfs(to, min(in, w));
        in -= res;
        out += res;
        edges[e].w -= res;
        edges[e^1].w += res;

        if (in == 0) break;  // 如果已经没有可以向外流的了，直接 break
    }
    if (out == 0) dis[u] = -1;  // 说明当前节点已经不能向外运输流量了，忽略不计
    return out;
}

void add(int u, int v, ll w) {
    addEdge(u, v, w);
    addEdge(v, u, 0);
}

ll maxflow() {
    ll ans = 0;
    while (bfs()) {
        ans += dfs(s, 1e18);
    }
    return ans;
}

ll w[maxn], val[maxn];
vector<int> adj[maxn];
int id[maxn][maxn];
int d[maxn][maxn];

int dep[maxn];
void dfs(int u, int p) {
    for (int v : adj[u]) {
        if (v == p) continue;
        dep[v] = dep[u] + 1;
        dfs(v, u);
    }
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    for (int i = 1; i <= n; i++) cin >> val[i];
    for (int i = 1; i <= n-1; i++) {
        int u,v; cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    int ID = 0;
    for (int k = 0; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            id[k][i] = ++ID;
        }
    }
    s = ++ID, t = ++ID;

    memset(d, 63, sizeof(d));
    for (int i = 1; i <= n; i++) {
        for (int j : adj[i]) d[i][j] = 1;
        d[i][i] = 0;
    }

    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
        }
    }

    for (int i = 1; i <= n; i++) {
        add(id[0][i], t, w[i]);
    }

    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            add(s, id[k][i], val[k] - val[k-1]);
            add(id[k][i], id[k-1][i], 1e18);
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            int k = d[i][j];
            add(id[k+1][i], id[0][j], 1e18);
        }
    }

    ll sum = (ll)n * val[n];
    ll res = maxflow();
    cout << sum - res << endl;
}

树形DP题解

这题还有个玄学的树形DP解法（我不能理解，先放在这）：

对于每个节点 $u$，设 dp[u][j] 为离 $u$ 的距离都 $\leq j$ 的所有节点均被加固了，dp的值为 $u$ 所在子树内的最优解之和。

则对于 $u$ 的每个直接的 child $v$，$v$ 可以选择加固周围 $\leq k$ 的所有节点，其中 $k = \{j-1,j,j+1\}$。

然后利用 探索当前子树 的思想来更新 dp[u][j]。

树形DP代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 222;

vector<int> adj[maxn];
int n, ans = 0;
int dp[maxn][maxn], w[maxn], val[maxn<<1];
void dfs(int u, int p) {
  dp[u][0] = 0;
  for (int j = 1; j <= n; j++) dp[u][j] = -w[u] + val[j];
 
  for (int v : adj[u]) {
      if (v == p) continue;
      dfs(v, u);

      int tmp[n+5];
      fill(tmp, tmp+n+5, -1e9);
      for (int j = 0; j <= n; j++) {
          for (int k = max(0,j-1); k <= min(n,j+1); k++) {
              tmp[j] = max({tmp[j], dp[u][j] + dp[v][k]});
          }
      }
      for (int j = 0; j <= n; j++) dp[u][j] = tmp[j];
 
  }
}
 
int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> w[i];
  for (int i = 1; i <= n; i++) cin >> val[i];
  for (int i = 1; i < n; i++) {
    int u,v; cin >> u >> v;
    adj[u].push_back(v);
    adj[v].push_back(u);
  }
  dfs(1,0);
  int ans = 0;
  for (int j = 0; j <= n; j++) {
    ans = max(ans, dp[1][j]);
  }
  cout << ans << endl;
}

例3 洛谷P2805 [NOI2009] 植物大战僵尸

题意

给定一个 $N \times M$ 的矩阵，每个格子内都有一个植物，每个植物拥有一个 score，代表吃掉这个植物以后会获得的分数（可以为负）。每个植物还有一个攻击位置集合，代表它可以攻击到的一些位置，它无法攻击它自己所在的位置。

现在我们可以放置僵尸，僵尸只能从某一行的最右侧开始向左走，如果僵尸来到了一个可以被植物攻击到的位置，它会立刻死亡，否则它可以吃掉这个植物并且继续向前走。

我们组织无限次僵尸攻击，并且每次攻击我们可以任选将僵尸放在哪一行。

求最大分数？

其中，$1 \leq N \leq 20, 1 \leq M \leq 30$。

题解

首先我们可以知道，这是一个格子之间互相保护的问题（保护有两种，一种是通过植物的攻击，第二种是同一行中，一个植物会保护它左边的那个植物）。

假如 $(x_1,y_1)$ 保护 $(x_2,y_2)$，这意味着如果我们吃了 $(x_2,y_2)$，则我们必须得吃 $(x_1,y_1)$。

这在有向图里表示的话就是 $(x_2,y_2) \rightarrow (x_1,y_1)$，所以问题变成了求最大权闭合子图。

不过我们需要注意，因为这个有向图中可能有环，怎么解决？

拓扑排序先把环求出来，然后求出环所保护的节点，一直拓展下去，最后我们可以知道：

所有环 + 所有被环直接/间接保护的节点都不可以被吃掉，所以直接将这些点删掉即可。

• 拓扑排序的时候，我们进行反向建边：假如 $(x_1,y_1)$ 保护 $(x_2,y_2)$，则建立 $(x_1,y_1) \rightarrow (x_2,y_2)$，这样的话拓扑排序求出来那些 deg > 0 的就是这些无法被吃掉的点了。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 605;
const int maxm = 8e5+5;

// 最大流板子略
int N,M,s,t, id[22][33], ID;
int score[22][33];
int head[maxn], ecnt = 2, cur[maxn], deg[maxn];  // ecnt 从 2 开始，方便取反向边
vector<int> adj[maxn];
bool ring[maxn];
void topo() {
    fill(ring, ring+maxn, 1);
    vector<int> tmp;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            if (!deg[id[i][j]]) tmp.push_back(id[i][j]);
        }
    }
    while (tmp.size()) {
        int u = tmp.back(); tmp.pop_back();
        ring[u] = 0;
        for (int v : adj[u]) {
            deg[v]--;
            if (!deg[v]) {
                tmp.push_back(v);
            }
        }
    }
}

vector<int> pos[22][33];
int main() {
    cin >> N >> M;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            id[i][j] = ++ID;
        }
    }
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            if (j > 1) adj[id[i][j]].push_back(id[i][j-1]), deg[id[i][j-1]]++;
            cin >> score[i][j];
            int w; cin >> w;
            while (w--) {
                int x,y; cin >> x >> y; x++,y++;
                pos[x][y].push_back(id[i][j]);
                adj[id[i][j]].push_back(id[x][y]);
                deg[id[x][y]]++;
            }
        }
    }
    topo();

    s = ++ID, t = ++ID;
    int sum = 0;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            if (ring[id[i][j]]) continue;
            if (score[i][j] > 0) add(s, id[i][j], score[i][j]), sum += score[i][j];
            if (score[i][j] < 0) add(id[i][j], t, -score[i][j]);
            if (j > 1 && !ring[id[i][j-1]]) add(id[i][j-1], id[i][j], 1e9);
            for (int p : pos[i][j]) {
                if (!ring[p]) {
                    add(id[i][j], p, 1e9);
                }
            }
        }
    }
    int res = maxflow();
    cout << max(0, sum - res) << endl;
}

最大权闭合子图

Contents

定义

闭合子图

最大权闭合子图

算法

结论

证明

例题

例1 洛谷P4174 [NOI2006] 最大获利

例2 CCPC2021威海 H city safety

例3 洛谷P2805 [NOI2009] 植物大战僵尸

参考链接