树套树
Contents
介绍
树套树常常用于解决一些二维数点问题。
经典的问题如:矩阵内查询和/最大值,更新矩阵内一个点的值等等。
在介绍树套树之前,先简单讲一下树状数组。
树状数组介绍
树状数组
树状数组的本质就是一个数组 tr[]。
其中 tr[x] 维护的是区间 [x-lowbit(x)+1, x] 的信息(即:以 x 为结尾,长度为 lowbit(x) 的区间)。
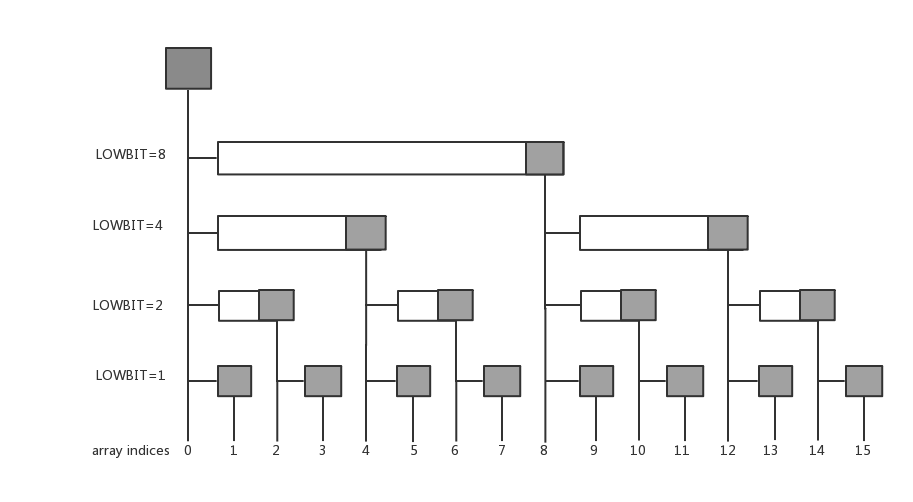
那么如果我们要询问 $[1,x]$ 的信息,那么可以利用 不断减去 lowbit(x) 的形式实现。
如果我们需要更新点 $x$ 的值,那么需要 不断加上 lowbit(x) 来保证所有包含了 $x$ 的区间都被更新了。
我们以 区间查询和,单点加值 为例:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5+5;
inline int lowbit(int x) { return x & -x; }
int tr[maxn];
int n, m;
void update(int p, int val) {
while (p <= n) {
tr[p] += val;
p += lowbit(p);
}
}
// return sum[1...p]
int query(int p) {
int ans = 0;
while (p > 0) {
ans += tr[p];
p -= lowbit(p);
}
return ans;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int x; cin >> x;
update(i, x);
}
while (m--) {
int op, x, y; cin >> op >> x >> y;
if (op == 1) update(x, y);
else cout << query(y) - query(x-1) << "\n";
}
}
• 注意一点,树状数组本质上维护的是 前缀信息,所以如果要询问区间信息,需要保证这个信息是 可减的。
比如 区间最大值 就不能用树状数组了(但是 前缀最大值 仍然可以用)。
树套树
所谓树套树,实际上就是将一个数据结构看作是两层线段树。
比如维护二维的矩阵信息,那么这个数据结构的外层线段树维护的是 $x$ 坐标,而内层线段树维护的则是 $y$ 坐标。
对于内层线段树来说,它和普通的一维线段树没有区别:每个节点维护的是一个区间,区间包含的是一些数字。
对于外层线段树:每个节点维护的是一个区间,区间包含的是一些内层线段树。
简单来说,相当于我们在每个 $x$ 坐标上,都开了一棵内层线段树。
而我们用外层线段树,维护了 $x$ 坐标的区间。
因此,我们在进行 矩阵查询/修改 时(例如 $[x_L,x_R][y_L,y_R]$),就分成了两步:
- 首先在外层线段树找到 $x$ 坐标所在的区间 $[x_L,x_R]$,它在外层线段树上对应的就是若干个节点。
- 进入这些节点(进入了以后就可以看到内层线段树了),然后对内层线段树进行 $[y_L,y_R]$ 的操作。
标记永久化
如果是 矩阵查询,单点修改 的话我们可以直接用树套树解决。
但是如果是 矩阵查询,矩阵修改 呢?
我们还是按照访问树套树的方式,但看起来我们需要对于 $[x_L,x_{L+1},…,x_R]$ 中的每一棵线段树都进行修改操作?
因为我们无法对外层线段树进行 pushup 或者 pushdown 操作,因为它维护的是线段树,而不是数值。
那么我们就引入了标记永久化的思想,什么意思呢?
简单来说,标记永久化就是 去除了 pushdown 操作,对于那些被修改操作完全覆盖的区间,直接给它打上一个标记。
之后,在询问的时候,当我们访问了一个节点时,我们就看一下这个节点上的标记,这时,标记的值就相当于 这个节点 之前被修改了,但是尚未下传 的信息。
所以询问时:
-
无论这个节点是否完全被我们的询问覆盖,我们都要把这个节点的标记,加入到我们的询问答案。
-
如果这个节点完全被覆盖,则我们直接考虑这个节点所维护的值即可,无需考虑标记了。
那么,在树套树的实现中,一般是通过 开两棵树套树:
一棵树套树,专门用来维护 原来的值。
另一棵树套树,专门用来维护 标记值。
然后在询问的时候,按照上面的两条规则进行操作,对内外两层线段树,写法基本一致。
例题
例1 洛谷P3287 [SCOI2014]方伯伯的玉米田
题意
给定 $n$ 个正整数 $a_i$,并且给定一个正整数 $K$。
每次操作我们可以选定一个区间 $[L,R]$,将 $[a_L … a_R]$ 内的所有值 + 1,操作最多进行 $K$ 次。
求操作后,最长不下降子序列(不一定连续)的长度?
其中,$n \in [1, 10000], K \in [1, 500], a_i \in [1,5000]$。
题解
首先,每次操作一个区间的话,右端点一定为 $n$(因为右边数字越大,LIS就有可能越长,所以让右边更大一些一定更好)。
然后就有了一个比较简单的 dp 思路:
设 dp[i][j] 代表:当前考虑前 $i$ 个元素,已经用掉了 $j$ 次操作,恰好以 $i$ 为结尾的最长 LIS 的长度。
然后我们不需要讨论当前用了多少个,我们直接用前面所有可能的状态进行转移:
$$dp[i][j] = \max\sum\limits_{i’ \in [1,i-1], j’ \in [0,j]} \{dp[i’][j’] + 1\}, ~ 其中 a[i] + j \geq a[i’] + j’。$$
总共有 $3$ 个条件(维度),这个东西怎么优化?
首先,如果我们将 $i$ 从小到大枚举,那么 $i$ 这一维可以直接忽略掉。
所以我们就剩下了 $a[i] + j$ 和 $j$ 这两个维度。
那么我们可以将 $a[i] + j$ 的值看作 $x$ 坐标,$j$ 的值看作 $y$ 坐标,那么转移方程就是:
$$dp[a[i]+j][j] = \max\sum\limits_{x \in [1,a[i] + j], y \in [0,j]} \{dp[x][y] + 1\}$$
那么这个东西本质上就是一个矩阵查询最大值,支持单点修改的结构。
$x$ 坐标的取值范围是 $[1,5500]$,$y$ 坐标的取值范围是 $[0,500]$。
二维线段树?不对,空间复杂度 $5500 * 501 * \log (5500) * \log(501)$ 约等于 1e9。
二维树状数组?空间复杂度刚好是 $5500 * 501$,可以过。
注意到,虽然我们维护的是最大值,但这实际上是一个 前缀最大值 的形式,所以可以用树状数组。
最后注意一下把 $y$ 变成 $[1,501]$ 即可。
二维树状数组代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int N = 5500, M = 501;
int tr[N+5][M+5];
inline int lowbit(int x) { return x&-x; }
void update(int x, int y, int val) {
int tmp = y;
while (x <= N) {
y = tmp;
while (y <= M) {
tr[x][y] = max(tr[x][y], val);
y += lowbit(y);
}
x += lowbit(x);
}
}
// 查询 [1...x][1...y]
int query(int x, int y) {
int tmp = y;
int ans = 0;
while (x > 0) {
y = tmp;
while (y > 0) {
ans = max(ans, tr[x][y]);
y -= lowbit(y);
}
x -= lowbit(x);
}
return ans;
}
int n, K;
int a[maxn];
int ans = 0;
int main() {
cin >> n >> K;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
for (int j = K; j >= 0; j--) {
int v = a[i] + j;
int res = query(v, j+1);
ans = max(ans, res + 1);
update(v, j+1, res + 1);
}
}
cout << ans << endl;
}
二维线段树代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int N = 5500, M = 500; // x:[1, 5500], y: [0, 500]
struct Node {
int maxval, lc, rc;
int rt; // 这个节点所维护的线段树的根
} tr[2e9]; // 开不了这么大的!
int rt = 0, ID = 0;
void insert_y(int& cur, int l, int r, int y, int val) {
if (!cur) cur = ++ID;
tr[cur].maxval = max(tr[cur].maxval, val);
if (l == r) return;
int mid = (l+r) >> 1;
if (y <= mid) insert_y(tr[cur].lc, l, mid, y, val);
if (y > mid) insert_y(tr[cur].rc, mid+1, r, y, val);
}
void insert_x(int& cur, int l, int r, int x, int y, int val) {
if (!cur) cur = ++ID;
tr[cur].maxval = max(tr[cur].maxval, val);
insert_y(tr[cur].rt, 0, M, y, val); // 从根节点开始
if (l == r) return;
int mid = (l+r) >> 1;
if (x <= mid) insert_x(tr[cur].lc, l, mid, x, y, val);
if (x > mid) insert_x(tr[cur].rc, mid+1, r, x, y, val);
}
// change the value of (x,y) to val
void insert(int x, int y, int val) {
insert_x(rt, 1, N, x, y, val);
}
int query_y(int cur, int l, int r, int yl, int yr) {
if (!cur) return 0;
int res = 0;
if (yl <= l && yr >= r) return tr[cur].maxval;
int mid = (l+r) >> 1;
if (yl <= mid) res = max(res, query_y(tr[cur].lc, l, mid, yl, yr));
if (yr > mid) res = max(res, query_y(tr[cur].rc, mid+1, r, yl, yr));
return res;
}
int query_x(int cur, int l, int r, int xl, int xr, int yl, int yr) {
if (!cur) return 0;
int res = 0;
if (xl <= l && xr >= r) {
return query_y(tr[cur].rt, 0, M, yl, yr);
}
int mid = (l+r) >> 1;
if (xl <= mid) res = max(res, query_x(tr[cur].lc, l, mid, xl, xr, yl, yr));
if (xr > mid) res = max(res, query_x(tr[cur].rc, mid+1, r, xl, xr, yl, yr));
return res;
}
int query(int xl, int xr, int yl, int yr) {
return query_x(rt, 1, N, xl, xr, yl, yr);
}
int n, K;
int a[maxn];
int ans = 0;
int main() {
cin >> n >> K;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
for (int j = K; j >= 0; j--) {
int v = a[i] + j;
int res = query(1, v, 0, j);
ans = max(ans, res + 1);
insert(v, j, res + 1);
}
}
cout << ans << endl;
}
例2 洛谷P3437 [POI2006]TET-Tetris 3D
题意
给定一个 $N \times M$ 的矩阵,有 $q$ 个询问,每次询问一个子矩阵内的最大值,并且将这个矩阵加上某个值。
求所有操作后,整个矩阵内的最大值?
其中,$q \leq 20000, N,M \leq 1000$。
题解
直接二维线段树维护即可,都不需要动态开点。这题是一个很好的板子。
对于最大值,我们注意到一个特性:只要一个矩阵中的任意一个元素被更新了,那么整个矩阵的最大值都要被更新。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
const int maxm = 30;
// 矩阵查询最大值
// 矩阵修改(加上值)
const int N = 1000;
struct Node {
int maxval;
int lazy; // 永久化标记(只打在内层线段树上)
};
struct SegY {
Node tr[maxn<<2];
void update(int cur, int l, int r, int L, int R, int val) {
tr[cur].maxval = max(tr[cur].maxval, val); // 如果 [l,r] 与 [L,R] 有交集直接更改
if (L <= l && R >= r) {
tr[cur].lazy = max(tr[cur].lazy, val); // 完全覆盖时,记录懒标记
return;
}
int mid = (l+r) >> 1;
if (L <= mid) update(cur<<1, l, mid, L, R, val);
if (R > mid) update(cur<<1|1, mid+1, r, L, R, val);
}
int query(int cur, int l, int r, int L, int R) {
int ans = 0;
ans = max(ans, tr[cur].lazy); // 懒标记值记录
if (L <= l && R >= r) {
ans = max(ans, tr[cur].maxval); // 正常查询
return ans;
}
int mid = (l+r) >> 1;
if (L <= mid) ans = max(ans, query(cur<<1, l, mid, L, R));
if (R > mid) ans = max(ans, query(cur<<1|1, mid+1, r, L, R));
return ans;
}
};
struct SegX {
SegY mx[maxn<<2], tag[maxn<<2];
void update(int cur, int l, int r, int xl, int xr, int yl, int yr, int val) {
mx[cur].update(1, 1, N, yl, yr, val); // 有交集就更新
if (xl <= l && xr >= r) {
tag[cur].update(1, 1, N, yl, yr, val); // 让被完全覆盖的这些线段树都更新一下 tag
return;
}
int mid = (l+r) >> 1;
if (xl <= mid) update(cur<<1, l, mid, xl, xr, yl, yr, val);
if (xr > mid) update(cur<<1|1, mid+1, r, xl, xr, yl, yr, val);
}
int query(int cur, int l, int r, int xl, int xr, int yl, int yr) {
int ans = 0;
ans = max(ans, tag[cur].query(1, 1, N, yl, yr)); // 懒标记下传
if (xl <= l && xr >= r) {
ans = max(ans, mx[cur].query(1, 1, N, yl, yr));
return ans;
}
int mid = (l+r) >> 1;
if (xl <= mid) ans = max(ans, query(cur<<1, l, mid, xl, xr, yl, yr));
if (xr > mid) ans = max(ans, query(cur<<1|1, mid+1, r, xl, xr, yl, yr));
return ans;
}
} tr;
int D, S, q;
// assign val to [xl,xr][yl,yr]
void update(int xl, int xr, int yl, int yr, int val) {
tr.update(1, 1, N, xl, xr, yl, yr, val);
}
// query maximum value between [xl,xr][yl,yr]
int query(int xl, int xr, int yl, int yr) {
return tr.query(1, 1, N, xl, xr, yl, yr);
}
int main() {
cin >> D >> S >> q;
while (q--) {
int n, m, h, x, y; cin >> n >> m >> h >> x >> y;
x++, y++; n--, m--;
int res = query(x, x+n, y, y+m);
update(x, x+n, y, y+m, res + h);
}
cout << query(1, N, 1, N) << "\n";
}
例3 洛谷P3688 [ZJOI2017] 树状数组
题意
现在有道题:
给定长度为 $n$ 的数组 $A$,初始值为 $0$,接下来进行 $m$ 次操作,每次操作有两种:
$1 ~ x$:将 $A_x$ 变成 $(A_x+1) \text{ mod } 2$
$2 ~ l ~ r$:询问 $\sum\limits_{i=l}^r A_i \text{ mod } 2$
九条可怜用树状数组解决这个问题,然而很可惜,她把树状数组的修改和前缀和询问操作的方向写反了,她写了如下程序:

现在,我们需要回答以下问题:
进行 $m$ 次操作,每次操作有两种:
$1 ~ l ~ r$:每次在区间 $[l,r]$ 内等概率选取一个 $x$,并且执行 $Add(x)$ (这里是指执行九条可怜写的错误程序)。
$2 ~ l ~ r$:询问 $Query(l,r)$ 得到正确结果的概率。
将答案输出为 $\frac{p}{q}$ 的形式,模 $998244353$。
其中,$n,m \leq 10^5$。
题解
如果我们熟悉树状数组的原理的话,就知道它正确的情况下,每次修改/询问维护的是前缀和。
那么现在这个错误的树状数组把两个方向都反过来了,那维护的就是后缀和了。
于是每次 $Query(l,r)$ 其实返回的是 suf[r] - suf[l-1] 的值。
当然注意到这个是在 $\text{mod } 2$ 下的,所以正负号没有区别。
所以 suf[r] - suf[l-1] = suf[l-1] - suf[r] $= \sum\limits_{i=l-1}^{r-1} A_i$
而正确的答案应该是 $\sum\limits_{i=l}^r A_i$,所以两者差的就是一个 $A_{l-1} + A_{r}$。
于是,原问题可以转化为:
$1 ~ l ~ r$ 仍然是等概率修改。
$2 ~ l ~ r$ 询问 $A_{l-1} = A_r$ 的概率。
怎么解决呢?一维线段树?每次修改给一个区间乘上一个概率?
似乎不行,因为这个题的修改操作是 $[l,r]$ 内有且仅有一个元素被修改,而一维线段树维护的概率包含了多个元素同时被修改的可能性。
一个神仙想法:二维线段树
我们将一个二元组 $(x,y)$ 定义为:$A_x, A_y$ 相等的概率。
所以每次修改 $[l,r]$,我们设 $p = \frac{1}{r-l+1}$,都会影响到三种这样的二元组:
- $x \in [l,r], y \in [l,r]$:那么 $(x,y)$ 有 $2*p$ 的概率被取反。
- $x \in [l,r], y \not\in [l,r]$:那么 $(x,y)$ 有 $p$ 的概率被取反。
- $x \not\in [l,r], y \in [l,r]$:那么 $(x,y)$ 有 $p$ 的概率被取反。
这实际上就是矩阵修改操作了。
那么对于每次询问,就只要询问 $(l-1,r)$ 这个点的概率即可。
那么这样的概率应该怎么维护?
我们给每个 node 都打上一个标记 $a$,代表 $x,y$ 相等的概率。
那么现在,设有 $b$ 的概率让 $x,y$ 继续保持相等。
那么 $x,y$ 在操作后,保持相等的概率就等于
$$ab + (1-a)(1-b)$$
所以我们定义一个特殊的乘法运算方式 $*$,其中
$$a*b = ab + (1-a)(1-b)$$
所以每次更新的时候,如果有 $p$ 的概率取反,那么就给所有对应的矩阵都 $*(1-p)$。
• 这个就用标记永久化进行维护即可。
• 因为 $n \leq 10^5$,所以必须动态开点,外层不用动态开,在外层维护一个 rt[maxn<<2] 即可,内层需要动态开点,这样总复杂度是 $O(n\log^2n)$ 的。
最后,我们注意到,当询问操作的 $l=1$ 时,这个错误程序返回的实际上是 $$suf[r] = \sum\limits_{i=r}^n A_i$$
而正确的答案是 $$pre[r] = \sum\limits_{i=1}^r A_i$$
所以询问的就是 $r$ 的前缀和与后缀和相等的概率。
这个可以直接用一维线段树维护,其中 $p_x$ 就代表 $x$ 的前缀和与后缀和相等的概率。
我们直接把这个一维线段树,维护在 $[0,0][y_1,y_2]$ 这个矩阵上,这样就不用特殊处理了。
每次修改 $[l,r]$ 时,前后缀和关系受到影响的位置有三种情况:
- $x \in [0, l-1]$:前缀和不变,后缀和一定变化,所以有 $1$ 的概率取反。
- $x \in [r+1, n]$:前缀和一定变化,后缀和不变,所以有 $1$ 的概率取反。
- $x \in [l,r]$:只有修改位置恰好在 $x$ 时,前后缀和的关系才不变,否则一定变化,所以有 $(1-\frac{1}{r-l+1})$ 的概率取反。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int N = 1e5;
template<class T>
T qpow(T a, int b) {
T res = 1;
while (b) {
if (b & 1) res *= a;
a *= a;
b >>= 1;
}
return res;
}
int norm(int x) {
if (x < 0) {
x += mod;
}
if (x >= mod) {
x -= mod;
}
return x;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(mod - x));
}
Z inv() const {
assert(x != 0);
return qpow(*this, mod - 2);
}
Z &operator*=(const Z &rhs) {
x = (ll)(x) * rhs.x % mod;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
};
inline Z mul(Z a, Z b) {
return (1-a) * (1-b) + a*b;
}
struct Node {
Z p = 1; // 相同的概率
int lc, rc;
};
int ID = 0;
struct SegY {
Node tr[maxn*400]; // 内层是动态开点的
void update(int& cur, int l, int r, int L, int R, Z val) {
if (!cur) cur = ++ID;
if (L <= l && R >= r) {
tr[cur].p = mul(tr[cur].p, val);
return;
}
int mid = (l+r) >> 1;
if (L <= mid) update(tr[cur].lc, l, mid, L, R, val);
if (R > mid) update(tr[cur].rc, mid+1, r, L, R, val);
}
Z query(int cur, int l, int r, int x) {
if (!cur) return 1;
if (l == r) return tr[cur].p;
int mid = (l+r) >> 1;
if (x <= mid) return mul(tr[cur].p, query(tr[cur].lc, l, mid, x));;
return mul(tr[cur].p, query(tr[cur].rc, mid+1, r, x));
}
} tag;
struct SegX {
int rt[maxn<<2]; // 外层无需动态开点
void update(int cur, int l, int r, int xl, int xr, int yl, int yr, Z val) {
if (xl <= l && xr >= r) {
tag.update(rt[cur], 0, N, yl, yr, val);
return;
}
int mid = (l+r) >> 1;
if (xl <= mid) update(cur<<1, l, mid, xl, xr, yl, yr, val);
if (xr > mid) update(cur<<1|1, mid+1, r, xl, xr, yl, yr, val);
}
Z query(int cur, int l, int r, int x, int y) {
Z d = tag.query(rt[cur], 0, N, y);
if (l == r) {
return d;
}
int mid = (l+r) >> 1;
if (x <= mid) return mul(d, query(cur<<1, l, mid, x, y));
return mul(d, query(cur<<1|1, mid+1, r, x, y));
}
} tr;
int n,m;
int main() {
cin >> n >> m;
while (m--) {
int op, l, r; cin >> op >> l >> r;
if (op == 1) {
Z p = Z(1) / Z(r-l+1);
// 修改二维情况,因为有规定 l <= r,所以更新矩阵的时候也遵循这个规定。
tr.update(1, 0, N, l, r, l, r, 1-2*p);
if (l > 1) tr.update(1, 0, N, 1, l-1, l, r, 1-p);
if (r < n) tr.update(1, 0, N, l, r, r+1, N, 1-p);
// 修改一维情况的前后缀和
tr.update(1, 0, N, 0, 0, 0, l-1, 0); // [0,l-1] 的前后缀和一定更改
tr.update(1, 0, N, 0, 0, r+1, N, 0); // 一定会修改 [r+1,N] 的前后缀和一定更改
tr.update(1, 0, N, 0, 0, l, r, p); // 只有修改这个位置时,才不会改变前后缀和的区别,否则都会改
} else {
Z res = tr.query(1, 0, N, l-1, r);
cout << res.val() << "\n";
}
}
}
