字符串Hash

介绍

字符串哈希可以在 $O(n)$ 时间内预处理一个字符串，然后在 $O(1)$ 的时间内查询任何字串的哈希值。

一般来讲我们从左往右 build 哈希值，一个 string $a_1a_2a_3…a_n$ 的哈希值为：

$$a_1 p^{n-1} + a_2 p^{n-2} + a_3 p^{n-3} + … + a_n p^0$$

其中 $a_i$ 为该字符的 ASCII值。

build 方法如下：

ll p[maxn];
int base = 31;
const int MOD = 1e9 + 7;
void p_init() {
    p[0] = 1;
    for (int i = 1; i <= maxn-1; i++) {
        p[i] = p[i-1] * base % MOD;
    }
}

求一个子串 $s[L,R]$ 的哈希值：只需要维护一个前缀和 $sum$，其中 $sum[R]$ 代表 $s[1…R]$ 的哈希值。

$$sum[R] = (a_1 p^{R-1} + a_2 p^{R-2} + … + a_{L-1} p^{R-L+1}) + (a_{L} p^{R-L} + … + a_R p^0)$$

$$sum[L-1] = a_1 p^{L-2} + a_2 p^{L-3} + … + a_{L-1} p^0$$

然后就有：

$$sum[R]-(sum[L] * p^{R-L+1}) = (a_{L} p^{R-L} + … + a_R p^0) = HASH(s[L…R])$$

总结：hash[L...R] = sum[R] - sum[L] * p[R-L+1]

应用

O(1) 判断回文串

对于原字符串进行一次预处理，反过来再预处理一次，然后判断 $s[L,R]$ 正过来和反过来的哈希值是否相等即可。

最长回文子串 $O(n)$

利用 DP：设 $R_i$ 为以 $i$ 结尾的最长回文的长度，那么答案为 $\max_{i=1}^n R_i$。

注意到 $R_i \leq R_{i-1} + 2$，所以每次暴力从 $R_{i-1} + 2$ 开始递减，找到第一个回文串为止。

复杂度：每次 $i$ 增大时，$R_{i}$ 增加 $2$，每次循环减少 $1$，所以复杂度为 $O(2n)$。

模版 (取模双哈希)

const int maxn = 5e5+5;
const int NUM = 2;
ll base[2] = {131, 137};
int MOD[2] = {(int)(1e9+7), (int)(1e9+9)};
ll p[maxn][NUM];

void p_init() {
    for (int j = 0; j < NUM; j++) {
        p[0][j] = 1;
        for (int i = 1; i <= maxn-1; i++) {
            p[i][j] = p[i-1][j] * base[j] % MOD[j];
        }
    }
}

struct StringHash {
    ll hs[maxn][NUM];
    int n;
    void init(string& s) {
        n = s.size();
        for (int j = 0; j < NUM; j++) {
            for (int i = 1; i <= n; i++) {
                hs[i][j] = (hs[i-1][j] * base[j] % MOD[j] + (ll)s[i-1]) % MOD[j];
            }
        }
    }
    // get the hash of j-th HASH function
    int gethash(int l, int r, int j) {
        return (hs[r][j] - hs[l-1][j] * p[r-l+1][j] % MOD[j] + MOD[j]) % MOD[j];
    }
    array<int, NUM> gethash(int l, int r) {
        array<int, NUM> res;
        for (int j = 0; j < NUM; j++) {
            res[j] = gethash(l, r, j);
        }
        return res;
    }
};

int n;
string s;
StringHash hs, rev_hs;
bool isPalindrome(int l, int r) {
    return hs.gethash(l, r) == rev_hs.gethash(n-r+1, n-l+1);
}

int main() {
    p_init();  // 先 init 所有p 的次方
    cin >> s >> t;
    n = s.size();
    hs.init(s);
    reverse(s.begin(), s.end());
    rev_hs.init(s);

    isPalindrome(1, n);  // 测试
}

模版 (自然溢出哈希)

自然溢出

没有 MOD 操作，依靠 unsigned long long 的 $2^{64}$ 自然溢出取模，速度快很多。

不是特别推荐这种方法，无论双哈希或者如何选择 base 都会被卡，卡自然溢出哈希的方法见这里

• 注意需要用 ull (unsigned long long)

const int maxn = 5e5+5;
const int NUM = 1;
ull base[2] = {131, 137};
ull p[maxn][NUM];  // 注意这里换成了 ull

void p_init() {
    for (int j = 0; j < NUM; j++) {
        p[0][j] = 1;
        for (int i = 1; i <= maxn-1; i++) {
            p[i][j] = p[i-1][j] * base[j];
        }
    }
}
 
struct StringHash {
    ull hs[maxn][NUM];
    string s;
    int n;
    void init() {
        n = s.size();
        for (int j = 0; j < NUM; j++) {
            for (int i = 1; i <= n; i++) {
                hs[i][j] = hs[i-1][j] * base[j] + s[i-1];
            }
        }
    }
    // get the hash of j-th HASH function
    ull gethash(int l, int r, int j) {
        return hs[r][j] - hs[l-1][j] * p[r-l+1][j];
    }
    array<ull, NUM> gethash(int l, int r) {
        array<ull, NUM> res;
        for (int j = 0; j < NUM; j++) {
            res[j] = gethash(l, r, j);
        }
        return res;
    }
};


int n;
string s;
StringHash hs, rev_hs;
bool isPalindrome(int l, int r) {
    return hs.gethash(l, r) == rev_hs.gethash(n-r+1, n-l+1);
}

int main() {
    p_init();  // 先 init 所有p 的次方
    cin >> s >> t;
    n = s.size();
    hs.s = s; rev_hs.s = s;;
    reverse(rev_hs.s.begin(), rev_hs.s.end());
    hs.init(); rev_hs.init();

    isPalindrome(1, n);  // 测试
}

例题

例1 CF1721E

题意

给定一个 string $s$，并且给定 $q$ 次询问，每次询问一个 string $t$，并且进行如下操作：

将 $t$ 连在 $s$ 后面。
询问 $|s|+1, |s|+2, …, |s|+|t|$ 位置的 prefix function
将字符串恢复为 $s$。

定义一个string $a$ 的 prefix function为：$p_1, p_2, …, p_{|a|}$，其中 $p_i$ 是最大的 $k$ 使得：

$k < i$ 且
$a[1…k] = a[i-k+1 … i]$

即最长的 $k$ 使得前缀等于后缀。

其中，$|s| \leq 10^6, q \leq 10^5, |t| \leq 10$

题解

首先我们可以发现，在 $t$ 连在 $s$ 后面时，我们可以很简单的处理哈希值。

现在考虑怎么计算 prefix function？

我们不能用哈希 + 二分，因为它不具有单调性，例如 abab，对于 $k=1$ 不成立，但是 $k=2$ 成立。

考虑另外一个方法：

如果前缀等于后缀，那么它应该是：

$$s_1 s_2 … s_k = s_{x} s_{x+1} … s_n t_1 t_2 … t_m$$

注意到我们可以拆成两段：

$$s_1 s_2 … s_{k-m} = s_{x} s_{x+1} … s_n$$

$$s_{k-m+1} … s_k = t_1 t_2 … t_m$$

前面一段实际上是 $s$ 本身的前缀后缀 matching，可以预处理。

后面一段是 $t$ 在 $s$ 里面的一个匹配。

所以问题转变成：

只要 $t$ 在 $s$ 中有一个匹配 $t = s[i … i+m-1]$，并且 $s[1…i-1] = s[n-i … n]$ 即可。

就剩下一个问题：如果要将 $t$ 在 $s$ 中匹配很多次，复杂度会爆炸。

鉴于 $|t| \leq 10$，我们可以对于每个位置 $i$ 都判断一下是否有前缀等于后缀，如果有，那么提前储存 $s[i…i], s[i…i+1] … s[i…i+m-1]$ 这些子串的哈希值，然后匹配即可。

最后注意一些边界情况：在一个位置的prefix function $> |s|$ 时没有考虑到，暴力枚举一下即可。

• 为了防止 map 爆炸，所以根据子串长度分开几个 map 来储存。

代码

#include <bits/stdc++.h>
using namespace std;
int qpow(ll a, ll b, ll P) {
    ll res = 1;
    while (b) {
        if (b & 1)
            res = res * a % P;
        a = a * a % P;
        b >>= 1;
    }
    return res;
}
 
const int NUM = 2;
struct StringHash {
    int hs[maxn][NUM];
    int MOD[NUM] = {(ll)1e9+7, (ll)1e9+9};
    int p[NUM] = {131, 137};
    int inv[maxn][NUM];
 
    string s;
    int n;
 
    void init() {
        n = s.size();
        for (int j = 0; j < NUM; j++) {
            int P = 1, invP = qpow(p[j], MOD[j]-2, MOD[j]);
            inv[0][j] = 1;
            for (int i = 1; i <= n; i++) {
                P = (ll)P * p[j] % MOD[j];
                inv[i][j] = (ll)inv[i-1][j] * invP % MOD[j];
                hs[i][j] = (hs[i-1][j] + (ll)s[i-1] * P % MOD[j]) % MOD[j];
            }
        }
    }
 
    void concat(string t) {
        int m = t.size();
        for (int j = 0; j < NUM; j++) {
            for (int i = n+1; i <= n+m; i++) inv[i][j] = hs[i][j] = 0;
            int P = qpow(p[j], n, MOD[j]), invP = qpow(p[j], MOD[j]-2, MOD[j]);
            for (int i = n+1; i <= n+m; i++) {
                P = (ll)P * p[j] % MOD[j];
                inv[i][j] = (ll)inv[i-1][j] * invP % MOD[j];
                hs[i][j] = (hs[i-1][j] + (ll)t[i-n-1] * P % MOD[j]) % MOD[j];
            }
        }
    }
 
    // get the hash of j-th HASH function
    int gethash(int l, int r, int j) {
        ll sum = (hs[r][j] - hs[l-1][j] + MOD[j]) % MOD[j];
        return sum * inv[l-1][j] % MOD[j];
    }
 
    array<int, NUM> gethash(int l, int r) {
        array<int, NUM> res;
        for (int j = 0; j < NUM; j++) {
            res[j] = gethash(l, r, j);
        }
        return res;
    }
} hs;
 
map<array<int, NUM>, int> mp[11];
int n,m;
int main() {
    cin >> hs.s;
    hs.init();
    n = hs.s.size();
    int Q; cin >> Q;
 
    for (int i = 1; i <= n-1; i++) {
        if (hs.gethash(1, i) == hs.gethash(n-i+1, n)) {
            for (int j = 1; j <= 10; j++) {
                if (i+j > n) break;
                array<int, NUM> h = hs.gethash(i+1, i+j);
                mp[j][h] = i;
            }
        }
    }
 
    while (Q--) {
        string t; cin >> t;
        hs.concat(t);
        m = t.size();

        for (int i = 1; i <= m; i++) {
            int ans = 0;
            int r = n+i;
            for (int j = 1; j <= min(2*m, n+i-1); j++) {
                if (hs.gethash(1, j) == hs.gethash(r-j+1, r)) ans = j;
            }
 
            auto h = hs.gethash(n+1, n+i);
            if (mp[i].count(h)) {
                ans = max(ans, i + mp[i][h]);
            }
 
            for (int j = n+i-1; j >= n; j--) {
                if (hs.gethash(1, j) == hs.gethash(n+i+1-j, n+i)) {
                    ans = max(ans, j);
                }
            }
 
            cout << ans << " ";
        }
 
        cout << "\n";
    }
}

例2 洛谷P4287 [SHOI2011]双倍回文

题意

如果一个字符串能写成 $ss^{-1}ss^{-1}$ 的形式，那么它是一个双倍回文。

给定一个字符串，求它的最长双倍回文子串长度。

其中，$n \leq 5 \times 10^5$。

回文串性质

首先明确一个性质：

对于一个长度为 $n$ 的字符串 $s$，它的本质不同的回文子串数量最多只有 $n$ 个。

证明：利用归纳。

对于 $n=1$ 显然成立，设对于 $n-1$ 都成立，那么当长度为 $n$ 时：

设 $s = tc$，其中 $t$ 为长度为 $(n-1)$ 的字符串，$c$ 是新加的字符，根据假设 $t$ 符合上述规则。

考虑以 $c$ 结尾的回文子串，假设它们的左端点从小到大排序为 $l_1, l_2, …, l_k$，则我们可以知道仅有 $s[l_1 … n]$ 可能为新增的回文串，因为对于任何 $l_j, j > 2$，$s[l_j … n] = s[l_1 … n + l_1 - l_j]$ 一定出现过了。

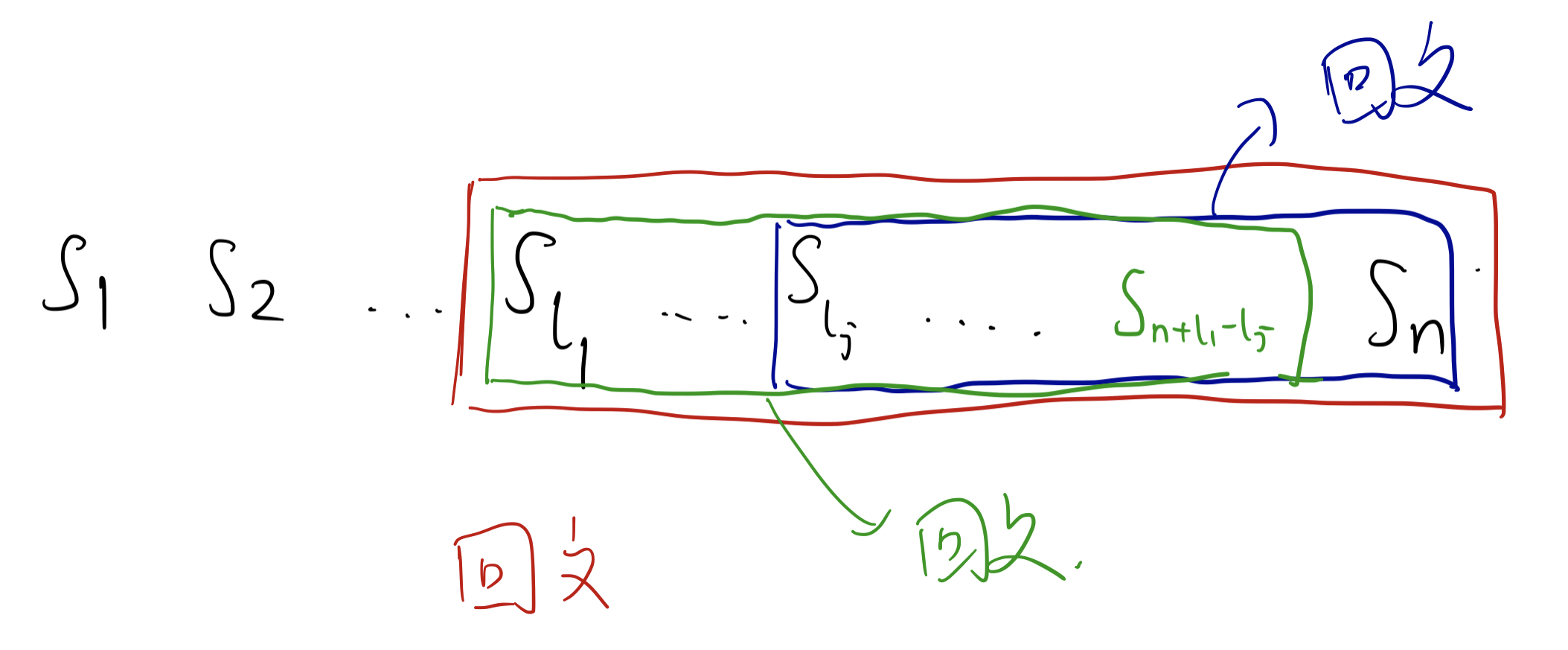
• 也就是说，在每次新增一个字符时，只用考虑以它为结尾的最长回文子串即可。

题解

首先我们知道，一个双倍回文子串一定是一个回文子串，所以它也遵循如上性质。

既然本质不同的回文子串数量只有 $n$ 个，那我们只要每一个都check一下是否符合双倍回文即可。

那么按照 $O(n)$ 的最长回文子串的做法，就是考虑了所有不同的回文子串。

如何在 $O(1)$ 时间内判断一个字符串是否为回文串/双倍回文串？

把原字符串 $s$ 反过来，复制一份为 $t$，然后在 $t$ 上再预处理一次hashing即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
const int maxn = 5e5+5;
const int maxm = 3e5+50;

int qpow(ll a, ll b, ll P) {
    ll res = 1;
    while (b) {
        if (b & 1)
            res = res * a % P;
        a = a * a % P;
        b >>= 1;
    }
    return res;
}

const int NUM = 2;
struct StringHash {
    int hs[maxn][NUM];
    int MOD[NUM] = {(ll)1e9+7, (ll)1e9+9};
    int p[NUM] = {131, 137};
    int inv[maxn][NUM];

    string s;
    int n;

    void init() {
        n = s.size();
        for (int j = 0; j < NUM; j++) {
            int P = 1, invP = qpow(p[j], MOD[j]-2, MOD[j]);
            inv[0][j] = 1;
            for (int i = 1; i <= n; i++) {
                P = (ll)P * p[j] % MOD[j];
                inv[i][j] = (ll)inv[i-1][j] * invP % MOD[j];
                hs[i][j] = (hs[i-1][j] + (ll)s[i-1] * P % MOD[j]) % MOD[j];
            }
        }
    }

    // get the hash of j-th HASH function
    int gethash(int l, int r, int j) {
        ll sum = (hs[r][j] - hs[l-1][j] + MOD[j]) % MOD[j];
        return sum * inv[l-1][j] % MOD[j];
    }

    array<int, NUM> gethash(int l, int r) {
        array<int, NUM> res;
        for (int j = 0; j < NUM; j++) {
            res[j] = gethash(l, r, j);
        }
        return res;
    }
} hs, hs2;

int n;
int dp[maxn];  // 以 i 结尾的回文串长度
bool isPalindrome(int l, int r) {
	return hs.gethash(l, r) == hs2.gethash(n-r+1, n-l+1);
}
bool check(int l, int r) {
    int len = r-l+1;
    if (len % 4) return 0;
    if (!isPalindrome(l,r)) return 0;
    if (!isPalindrome(r-len/2+1, r)) return 0;
    return 1;
}

int main() {
    cin >> n;
    cin >> hs.s;
    hs.init();
    hs2.s = hs.s;
    reverse(hs2.s.begin(), hs2.s.end());
    hs2.init();
    int ans = 0;

    for (int i = 1; i <= n; i++) {
        for (int len = min(i, dp[i-1]+2); len >= 1; len--) {
            if (check(i-len+1, i)) ans = max(ans, len);
            if (isPalindrome(i-len+1, i)) {
                dp[i] = len;
                break;
            }
        }
    }

    cout << ans << endl;
}

例3 ICPC2018南京M Mediocre String Problem

题意

给定两个string $s,t$，求满足以下条件的三元组 $(i,j,k)$ 的数量：

$1 \leq i \leq j \leq |s|$
$1 \leq k \leq |t|$
$j-i+1 > k$
$s[i…j] + t[1…k]$ 是一个回文串。

其中 $s \in [2, 10^6], t \in [1, |s|)$

题解

我们看第四条：如果 $s[i…j] + t[1…k]$ 是一个回文串，因为第三条规定了 $s[i…j]$ 是比 $t[1…k]$ 长的，所以我们可以把 $s[i…j]$ 分成两个部分：

$s[i…i+k-1]$ 和 $s[i+k…j]$，其中：

$s[i…i+k-1]$ 反过来和 $t[1…k]$ 完全一样。
$s[i+k…j]$ 是一个回文串。

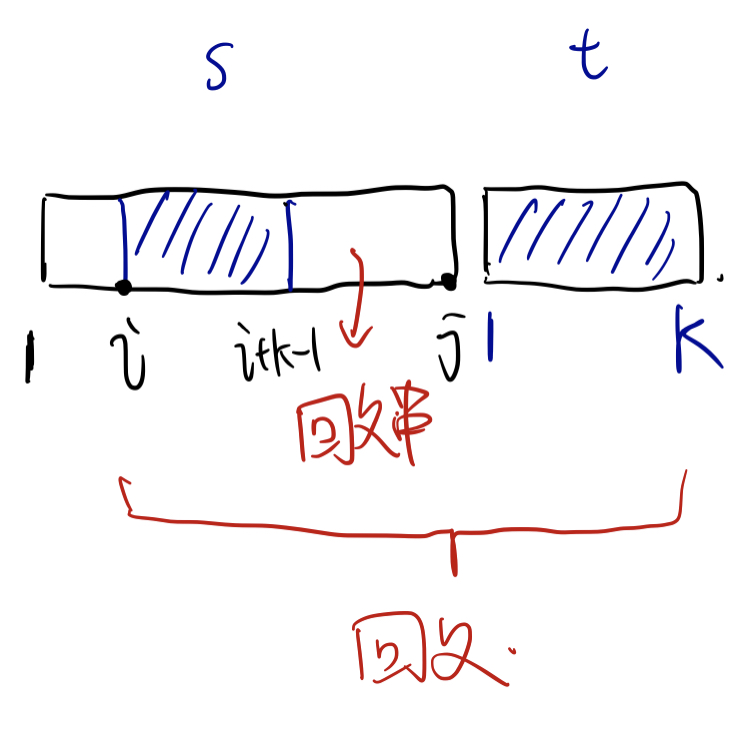
并且假如我们固定 $i+k-1$ 这个位置，并且让 $i$ 逐渐增大，$k$ 随之减小，那么 $(i,j,k)$ 仍然是一个回文串。

我们需要知道：以 $i+k-1$ 开头的回文串有多少个？这个值乘上 $k$ 就是固定了这个 $i+k-1$ 的值对答案的贡献了。

考虑如下问题：以 $i$ 开头的回文串有几个？

一般对于这种问题，我们需要考虑固定一个点来哈希+二分，这里固定开头或者结尾是不行的，那固定对称中心呢？是可行的。

所以我们枚举对称中心，然后利用哈希+二分求出最长的回文半径，用差分数组进行区间加即可。

• 注意枚举奇数和偶数两种情况。

有了上述信息，我们只要枚举 $i+k-1$ 的值，然后将 $t$ 先反转过来得到 $t_r$，那么每次要找的就是

$s[1…i+k-1]$ 与 $t_r[1…|t|]$ 的最长后缀，同样用哈希+二分即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
ull base = 131;
ull p[maxn];
 
void p_init() {
    p[0] = 1;
    for (int i = 1; i <= maxn-1; i++) {
        p[i] = p[i-1] * base;
    }
}
 
struct StringHash {
    ull hs[maxn];
    string s;
    int n;
    void init() {
        n = s.size();
        for (int i = 1; i <= n; i++) {
            hs[i] = hs[i-1] * base + s[i-1];
        }
    }
    ull gethash(int l, int r) {
        return hs[r] - hs[l-1] * p[r-l+1];
    }
};
 
int n,m;
int st[maxn];  // st[i]: the number of palindromes index starts with i (in s)
 
string s,t;
StringHash hs, rev_hs, rev_ht;
bool isPalindrome(int l, int r) {
    return hs.gethash(l, r) == rev_hs.gethash(n-r+1, n-l+1);
}
void init_st() {
    // 枚举奇数长度的回文串
    for (int mid = 1; mid <= n; mid++) {
        int l = 0, r = min(mid-1, n-mid);
        int res = 0;
        while (l <= r) {
            int c = (l+r) >> 1;
            int L = mid-c, R = mid+c;
            if (isPalindrome(L, R)) {
                res = c;
                l = c + 1;
            } else r = c - 1;
        }
        st[mid-res]++;
        st[mid+1]--;
    }
 
    // 偶数长度的回文串
    for (int mid = 1; mid < n; mid++) {
        if (s[mid-1] != s[mid]) continue;  // 这里特判一下
        int l = 0, r = min(mid-1, n-mid-1);
        int res = 0;
        while (l <= r) {
            int c = (l+r) >> 1;
            int L = mid-c, R = mid+1+c;
            if (isPalindrome(L, R)) {
                res = c;
                l = c + 1;
            } else r = c - 1;
        }
        st[mid-res]++;
        st[mid+1]--;
    }
 
    for (int i = 1; i <= n; i++) st[i] = st[i] + st[i-1];
}
 
 
int main() {
    p_init();
    cin >> s >> t;
    n = s.size(), m = t.size();
    hs.s = s; rev_hs.s = s; rev_ht.s = t;
    reverse(rev_hs.s.begin(), rev_hs.s.end());
    reverse(rev_ht.s.begin(), rev_ht.s.end());
    hs.init(); rev_hs.init(); rev_ht.init();
 
    init_st();  // init the start array
 
    ll ans = 0;
    for (int x = 1; x <= n-1; x++) {
        // 匹配 s[1...x] 与 rev_t[] 的最长后缀
        int l = 1, r = min(x, m);
        int res = 0;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (hs.gethash(x-mid+1, x) == rev_ht.gethash(m-mid+1, m)) {
                res = mid;
                l = mid + 1;
            } else r = mid - 1;
        }
        ans += (ll)st[x+1] * (ll)res;
    }
    cout << ans << "\n";
}

例4 Atcoder ABC135F. Strings of Eternity

题意

给定两个string $s,t$，求一个最大的 $i$，使得存在一个 $j \geq 0$，使得 $t$ 的 $i$ 个copy是 $s$ 的 $j$ 个copy的一个substring。

如果这个 $i$ 可能是无穷大，输出 $-1$。

题解

思路巧妙的图论题。

我们先考虑 $i=1$ 的情况，这说明 $t$ 从 $s$ 的一个后缀开始，经过 $s$ 的一些copy，然后到 $s$ 的某一个前缀结束。

所以可以看作是从 $s$ 的一个index $u$ 到了另外一个index $v$。

于是我们连边 $(u,v+1)$。

那么 $i > 1$ 的情况就可以递推得到：也就是顺着这些边走 $i$ 次。

所以如果最后图中有环，就是 $-1$，没有环的话，只要看在图中最深能走多远即可。

• 我们用字符串哈希来 $O(1)$ 找出每一个 $u$ 出发，能走到哪个 $v$。

代码

#include <bits/stdc++.h>
using namespace std;
StringHash hs, ht;
vector<int> adj[maxn];
int dp[maxn], vis[maxn];
bool ok = 1;
int ID = 0;
void dfs(int u, int p) {
    dp[u] = 0;
    vis[u] = ID;
    for (int v : adj[u]) {
        if (dp[v] != -1 && vis[v] == ID) {
            ok = 0;
            return;
        }
        dfs(v, p);
        dp[u] = dp[v] + 1;
    }
}

int main() {
    p_init();
    string s, t;
    cin >> s >> t;
    int n = s.size(), m = t.size();
    while (s.size() < 1e6) s += s;
    hs.s = s;
    ht.s = t;
    hs.init();
    ht.init();
    for (int i = 1; i <= n; i++) {
        if (hs.gethash(i, i+m-1) == ht.gethash(1, m)) {
            int R = i + m;  // [1...n], [n+1...2n]
            R %= n;
            if (!R) R = n;
            adj[i].push_back(R);
        }
    }
    memset(dp, -1, sizeof(dp));
    memset(vis, -1, sizeof(vis));
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        if (dp[i] == -1) {
            dfs(i, ++ID);
            ans = max(ans, dp[i]);
        }
    }
    if (ok) cout << ans << endl;
    else cout << -1 << endl;
}

例5 CF710F. String Set Queries

题意

初始状态下给定一个空的集合 $D$，给定 $m$ 个询问，询问有 3 种：

将一个 string $s$ 加入集合 $D$。
将一个 string $s$ 从集合 $D$ 中删除。
给定一个字符串 $s$，回答 $D$ 中的所有字符串，在 $s$ 中出现的次数之和。

例如：D = {"a", "abc"}, s = "aabc"，那么 "a" 出现了 $2$ 次，而 "abc" 出现了 $1$ 次，所以本次询问答案为 $3$。

其中，$m \leq 3 \times 10^5$，所有询问中的所有字符串的长度和不超过 $3 \times 10^5$，询问强制在线。

题解

经典套路：注意到字符串的不同长度只有 $\sqrt {3 \times 10^5}$ 种。

我们直接将所有 $D$ 中的字符串哈希一下，然后将其哈希值根据字符串长度放在相应的 set 里面。

在询问 $3$ 出现时，直接哈希这个字符串 $s$，并且暴力枚举 $s$ 的每一个开头，并查询当前 $D$ 中存在的所有长度（最多 $\sqrt {3 \times 10^5}$ 种）中的 set，询问其对应长度的哈希值是否存在。

最终复杂度 $m \sqrt m$，用单哈希（取模）勉强能卡过去。

代码

#include <bits/stdc++.h>
using namespace std;
const int NUM = 1;
ll base[2] = {131, 137};
int MOD[2] = {(int)(1e9+7), (int)(1e9+9)};
ll p[maxn][NUM];

void p_init() {
    for (int j = 0; j < NUM; j++) {
        p[0][j] = 1;
        for (int i = 1; i <= maxn-1; i++) {
            p[i][j] = p[i-1][j] * base[j] % MOD[j];
        }
    }
}

ll tmp[maxn][NUM];
void cal_hash(string& s) {
    int n = s.size();
    for (int j = 0; j < NUM; j++) {
        for (int i = 1; i <= n; i++) {
            tmp[i][j] = (tmp[i-1][j] * base[j] % MOD[j] + (ll)s[i-1]) % MOD[j];
        }
    }
}

struct StringHash {
    ll hs[maxn][NUM];
    int n;
    void init(string& s) {
        n = s.size();
        for (int j = 0; j < NUM; j++) {
            for (int i = 1; i <= n; i++) {
                hs[i][j] = (hs[i-1][j] * base[j] % MOD[j] + (ll)s[i-1]) % MOD[j];
            }
        }
    }
    // get the hash of j-th HASH function
    int gethash(int l, int r, int j) {
        return (hs[r][j] - hs[l-1][j] * p[r-l+1][j] % MOD[j] + MOD[j]) % MOD[j];
    }
    array<int, NUM> gethash(int l, int r) {
        array<int, NUM> res;
        for (int j = 0; j < NUM; j++) {
            res[j] = gethash(l, r, j);
        }
        return res;
    }
} hs;

set<string> se[maxn];
int cnt[maxn];
unordered_set<int> have;
unordered_set<ll> hashset[maxn];

int main() {
    p_init();
    int M; cin >> M;
    while (M--) {
        int t; string s; cin >> t >> s;
        int n = s.size();
        if (t == 1) {
            se[n].insert(s);
            cnt[n]++;
            if (cnt[n] == 1) have.insert(n);
            cal_hash(s);
            ll val = tmp[n][0];
            hashset[n].insert(val);
        } else if (t == 2) {
            se[n].erase(s);
            cnt[n]--;
            if (cnt[n] == 0) have.erase(n);
            cal_hash(s);
            ll val = tmp[n][0];
            hashset[n].erase(val);
        } else {
            hs.init(s);
            int res = 0;
            for (int i = 1; i <= n; i++) {
                for (int len : have) {
                    if (i + len - 1 <= n) {
                        ll val = hs.gethash(i, i+len-1, 0);
                        if (hashset[len].count(val)) res++;
                    }
                }
            }
            cout << res << endl;
        }
    }
}

Contents

介绍

应用

O(1) 判断回文串

最长回文子串 $O(n)$

模版 (取模双哈希)

模版 (自然溢出哈希)

例题

例1 CF1721E

例2 洛谷P4287 [SHOI2011]双倍回文

例3 ICPC2018南京M Mediocre String Problem

例4 Atcoder ABC135F. Strings of Eternity

例5 CF710F. String Set Queries