SWERC 2021-2022

D. Evolution of Weasels

题意

给定两个字符串 $s,t$，字符串中仅包含 $ABC$ 这三个字母。

我们对于 $s$ 可以在任意位置增加/删除子串 $AA,BB,CC,ABAB,BCBC$。

求是否存在一种方式让 $s$ 变成 $t$？

其中，$|s|, |t| \in [1, 200]$。

题解

一开始想的是 editing distance，但有个反例：

$s =$"CBCBCC"，$t =$ "ABAB"，这里 $s$ 应该从中间删掉 BCBC，然后删掉 CC，最后添加 ABAB，答案应该是 YES。

以下是正解：

观察这些子串，发现它们每个字母都包含了偶数个，并且我们还能发现 $B$ 出现的频率很高。

我们会发现，$B$ 其实是可以在整个串中随意移动的！

以下先给出一些引理：

BABA 与 CBCB 可以直接删掉。

证：BABA -> AA[BABA]BB -> A[ABAB]ABB -> AABB -> ，对于 CBCB 同理。

对于 AB，我们有办法将它变成 BA：

证：AB -> BB[AB]AA -> B[BABA]A -> BA

同理可得 AB <-> BA, BC <-> CB。

这说明 B 我们可以全部移动到最右边然后消掉，并且 B 的奇偶性无法变化，所以如果 $s,t$ 中 B 数量的奇偶性不同，则答案为 NO。

最后我们可以发现 A,C 的相对顺序不能变化，所以把 B 全部消掉以后只要拿栈维护一下 A,C 看最终情况是否相同即可。

代码

#include <bits/stdc++.h>
using namespace std;
int T;
int main() {
    cin >> T;
    while (T--) {
        string s,t; cin >> s >> t;
        int bs = 0, bt = 0;
        for (char c : s) {
            if (c == 'B') bs++;
        }
        for (char c : t) {
            if (c == 'B') bt++;
        }
        if ((bs&1) != (bt&1)) {
            cout << "NO\n";
            continue;
        }
        stack<char> st1, st2;
        for (char c : s) {
            if (c == 'B') continue;
            if (st1.size() && st1.top() == c) {
                st1.pop();
            } else {
                st1.push(c);
            }
        }
        for (char c : t) {
            if (c == 'B') continue;
            if (st2.size() && st2.top() == c) {
                st2.pop();
            } else {
                st2.push(c);
            }
        }
 
        if (st1.size() != st2.size()) {
            cout << "NO\n";
            continue;
        }
 
        bool ok = 1;
        while (st1.size()) {
            if (st1.top() != st2.top()) {
                ok = 0;
            }
            st1.pop(); st2.pop();
        }
        cout << (ok ? "YES" : "NO") << endl;
 
    }
}

F. Antennas

题意

有 $n$ 个天线塔排列在一条直线上，第 $i$ 个天线塔位于位置 $i$，拥有一个信号水平 $p_i$。

两个天线塔 $i,j$ 之间可以双向交流，当且仅当 $|i-j| \leq \min(p_i,p_j)$。

给定 $a,b$，求信号塔 $a$ 到 $b$ 的最短路径长度？

其中，$n \leq 2 \times 10^5, a,b,p_i \in [1, n]$。

题解

这题就是一个图上跑 bfs 找最短路（因为权值均为 $1$），但图的点和边太多了，该怎么办？

对于点 $i$，它可以覆盖到的范围为 $[i-p_i, i+p_i]$，但覆盖到的这些点 $j$ 不一定能与 $i$ 相连。

所以我们只要找到一个范围内，有哪些满足条件的点 $j$ 即可。

考虑两个部分：

$j > i$，只要 $p_j \geq j-i$，即 $p_j - j \geq -i$ 即可。
$j < i$，只要 $p_j \geq i-j$，即 $p_j + j \geq i$ 即可。

所以对于 $i$，只要分成两个区间：

$[i+1, i+p_i]$ 内，寻找 $j$ 使得 $p_j - j > -i$。
$[i-p_i, i-1]$ 内，寻找 $j$ 使得 $p_j + j \geq i$ 即可。

用线段树就可以解决了，并且我们其实每次只需要找到一个满足条件的 $j$ 即可，找到一个以后就把 $p_j$ 设为 $-\infty$，然后继续找 $j$，直到找不到为止。

具体来说，维护两个线段树，分别维护区间内 $p_j - j$ 和 $p_j + j$ 的最大值和对应的index $j$。

这样就可以跑 bfs 了，每个 $j$ 只会被用一次，复杂度为 $O(n\log n)$。

代码

#include <bits/stdc++.h>
using namespace std;
struct State {
    int val, idx;
    bool operator<(const State& other) const {
        if (val == other.val) return idx < other.idx;
        return val > other.val;
    }
};

struct Tree_Node {
    int maxval, maxidx;
} tr1[maxn<<2], tr2[maxn<<2];
int p[maxn];
int n, st, ed;
void merge_set(set<State>& s1, set<State>& s2, set<State>& s3) {
    for (State s : s1) s3.insert(s);
    for (State s : s2) s3.insert(s);
}

void push_up(Tree_Node* tr, int cur) {
    tr[cur].maxval = -1e9;
    if (tr[cur<<1].maxval > tr[cur].maxval) {
        tr[cur].maxval = tr[cur<<1].maxval;
        tr[cur].maxidx = tr[cur<<1].maxidx;
    }
    if (tr[cur<<1|1].maxval > tr[cur].maxval) {
        tr[cur].maxval = tr[cur<<1|1].maxval;
        tr[cur].maxidx = tr[cur<<1|1].maxidx;
    }
}

void build(Tree_Node* tr, int cur, int l, int r, int f) {
    if (l == r) {
        tr[cur] = {p[l] + f*l, l};
        return;
    }
    int mid = (l+r) >> 1;
    build(tr, cur<<1, l, mid, f);
    build(tr, cur<<1|1, mid+1, r, f);
    push_up(tr, cur);
}

void del(Tree_Node* tr, int cur, int l, int r, int x, int f) {
    if (l == r) {
        tr[cur].maxidx = -1;
        tr[cur].maxval = -1e9;
        return;
    }
    int mid = (l+r) >> 1;
    if (x <= mid) del(tr, cur<<1, l, mid, x, f);
    else del(tr, cur<<1|1, mid+1, r, x, f);
    push_up(tr, cur);
}

void Del(int x) {
    del(tr1, 1, 1, n, x, 1);
    del(tr2, 1, 1, n, x, -1);
}

vector<int> tmp;  // 用于储存满足条件的index

void query(Tree_Node* tr, int cur, int l, int r, int L, int R, int val) {
    if (L <= l && R >= r) {
        if (tr[cur].maxval >= val) {
            tmp.push_back(tr[cur].maxidx);
        }
        return;
    }
    int mid = (l+r) >> 1;
    if (L <= mid) query(tr, cur<<1, l, mid, L, R, val);
    if (R > mid) query(tr, cur<<1|1, mid+1, r, L, R, val);
}

// 寻找满足 p[j] + f*j >= val 的
void Query(Tree_Node* tr, int L, int R, int val) {
    tmp.clear();
    L = max(L, 1);
    R = min(R, n);
    if (L <= R)
        query(tr, 1, 1, n, L, R, val);
}

int dis[maxn];
int main() {
    int T; cin >> T;
    while (T--) {
        cin >> n >> st >> ed;
        for (int i = 1; i <= n; i++) cin >> p[i], dis[i] = 1e9;
        build(tr1, 1, 1, n, 1);
        build(tr2, 1, 1, n, -1);
        queue<int> q;
        q.push(st);
        dis[st] = 0;
        Del(st);
        while (q.size()) {
            int i = q.front(); q.pop();
            bool done = 0;
            while (!done) {
                done = 1;
                Query(tr1, i-p[i], i-1, i);
                if (tmp.size()) done = 0;

                for (int j : tmp) {
                    dis[j] = dis[i] + 1;
                    Del(j);
                    q.push(j);
                }

                Query(tr2, i+1, i+p[i], -i);
                if (tmp.size()) done = 0;

                for (int j : tmp) {
                    dis[j] = dis[i] + 1;
                    Del(j);
                    q.push(j);
                }
            }
        }
        cout << dis[ed] << "\n";
    }
}

N. Drone Photo

题意

在一个 $n \times n$ 的网格中，每个格子有一个 $\in [1, n^2]$ 的数字，格子内数字各不相同。

求有多少个矩形，使得这个矩形的四个角中，最小的两个值所在的位置不是对角。（即，最小的两个值如果连一条线在中间，一定是矩形的一条边，而不是对角线）。

其中，$n \leq 1500$。

题解

我们发现，如果对于一个点 $(i,j)$，只要与它同一行/同一列的值，一个比它大，一个比它小即可，不需要管对角的第四个值。

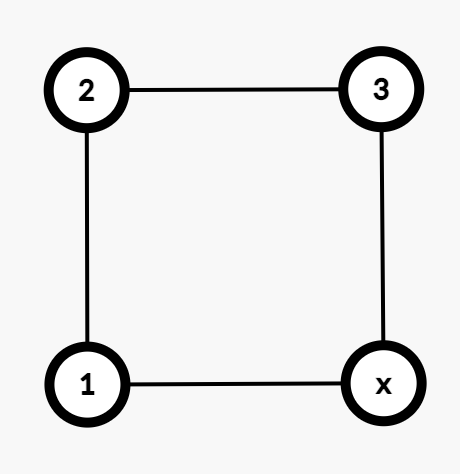
这里，考虑的点为 $2$，很容易发现，无论 $x$ 的值为多少，这个矩形一定满足条件。

我们只需要证明：

一个矩形满足条件，当且仅当矩形的四个角中存在一个角 $(i,j)$，使得与它同一行/同一列的角，一个比它大，一个比它小。

上面我们已经证明了 $\leftarrow$ 这个方向，接下来证明 $\rightarrow$。

假设一个矩形满足条件，但是不存在这样的角 $(i,j)$，那么我们选取最小的那个角，可以画出如下情况：

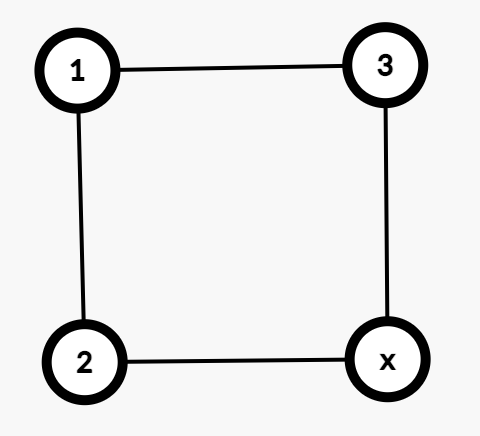
可以发现，无论 $x$ 取什么值，要么最小的两个值是对角，要么存在一个角使得同一行列中一个比它大，另外一个比它小。

所以得证。

所以对于每个点 $(i,j)$，设第 $i$ 行有 $A$ 个比它小的数字，第 $j$ 列有 $B$ 个比它小的数字，那么这个点的贡献就是

$$A * (n-1-B) + B * (n-1-A)$$

最后答案就是所有贡献之和除以 $2$。

我们可以通过 $O(n^2)$ 的复杂度对于所有点 $(i,j)$ 找出对应的 $A,B$（更高的复杂度会T，本题卡常）：

注意到所有的值位于 $[1, n^2]$ 之间且互不相同，所以不妨直接从 $1$ 枚举到 $n^2$，枚举到值 $x$ 时我们可以知道 $x$ 所在的坐标 $(i,j)$，此时我们知道之前枚举的所有值都小于 $x$，所以可以直接利用两个数组 R[], C[] 来记录第 $i$ 行已经有几个数了，第 $j$ 列有几个数，统计完以后将 R[i]++; C[j]++; 即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1505;
int n;
pii pos[maxn*maxn];
int row[maxn][maxn], col[maxn][maxn];  // 记录row/col 内有多少个比 (i,j) 小。

int R[maxn], C[maxn];  // 记录枚举到x时，row[i] 中有多少个小于 x 的数，col[j] 中有多少个小于 x 的数
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            int a; cin >> a;
            pos[a] = {i,j};
        }
    }
    
    for (int x = 1; x <= n*n; x++) {
        int i = pos[x].first, j = pos[x].second;
        row[i][j] = R[i];
        col[i][j] = C[j];
        R[i]++, C[j]++;
    }

    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            ll r = row[i][j], c = col[i][j];
            ans += r * (n-1-c) + c * (n-1-r);
        }
    }
    cout << ans/2 << endl;
}

Contents

D. Evolution of Weasels

F. Antennas

N. Drone Photo