2020-2021 ICPC, NERC, Southern and Volga Russian Regional Contest

G. Hobbits

题意

二维平面上有 $n$ 个点，第 $i$ 个点的坐标是 $(x_i,y_i)$，其中 $x_i < x_{i+1}, \forall i \in [1, n-1]$，点 $i$ 与点 $(i+1)$ 之间由一条线段链接。

在 $(x_n, y_n + H)$ 位置有一个眼睛，现在从点 $1$ 沿着线段走到点 $n$，求这个眼睛的视野能覆盖这个路程中的多长距离？

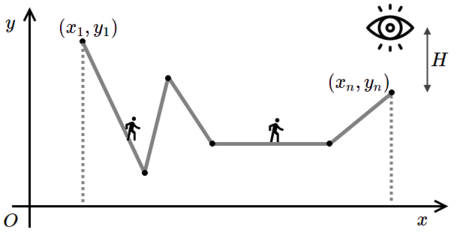
其中，$2 \leq n \leq 2 \cdot 10^5, H \in [1, 10^4], x_i \in [0, 4 \cdot 10^5], y_i \in [0 \leq 10^4]$。

题解

几何题。这里用的是 kuangbin的板子，并且有板子相对应的讲解

我们设这个眼睛为 $s$，那么可以知道 $(x_n,y_n)$ 在 $s$ 的正下方，接着视线顺时针旋转，每次碰到一个点就判断这个点是否能被看到。

可以知道，这个点能被看见，当且仅当它前面没有点（或相应的线段）能挡住它，判断是否能挡住只要看顺时针扫描的时候的夹角即可，如果右边有个点对应的角更大的话就看不见了。

如果能看见点 $i$，记录这个点为 $pre$，在看见下一个点 $i$ 时，链接 $(s,pre)$ 并且做延长线，与线段 $(i,i+1)$ 相交即可得到对应路程长度。

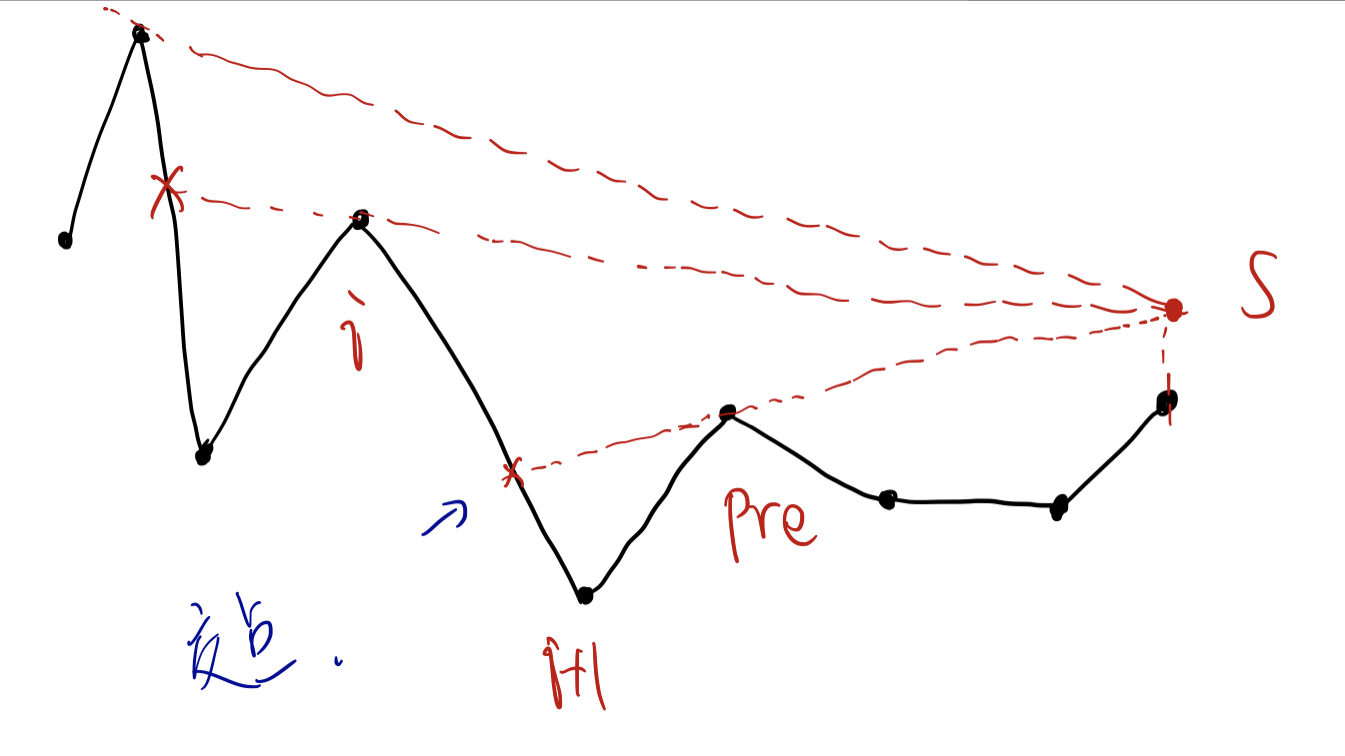
最后注意特判一下平行的情况，如图：

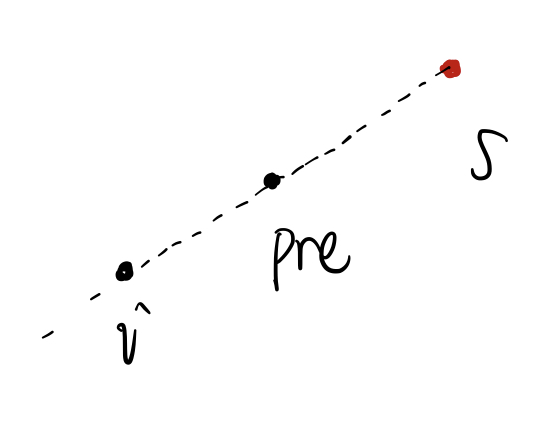
如果 $(i,pre)$ 之间刚好是一条线段（这意味着 $pre=i+1$），并且 $s,pre,i$ 在同一条线上，那么是 $(i,pre)$ 整条可以计入答案的。

这里要注意使用 long long 或者板子里的 parallel() 函数来判断，如果用夹角判断会出现精度问题！

• 最后，注意用 scanf() 读入数据，否则超时。

代码

#include <bits/stdc++.h>
using namespace std;
int sgn(double x){
	if(fabs(x) < eps)return 0;
	if(x < 0)return -1;
	else return 1;
}
//square of a double
inline double sqr(double x){return x*x;}
 
struct Point{
	double x,y;
	Point(){}
	Point(double _x,double _y){
		x = _x;
		y = _y;
	}
	void input(){
		scanf("%lf%lf",&x,&y);
	}
	void output(){
		printf("%.2f %.2f\n",x,y);
	}
	bool operator == (Point b)const{
		return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
	}
	bool operator < (Point b)const{
		return sgn(x-b.x)== 0?sgn(y-b.y)<0:x<b.x;
	}
	Point operator -(const Point &b)const{
		return Point(x-b.x,y-b.y);
	}
	//叉积
	double operator ^(const Point &b)const{
		return x*b.y - y*b.x;
	}
	//点积
	double operator *(const Point &b)const{
		return x*b.x + y*b.y;
	}
	//返回长度
	double len(){
		return hypot(x,y);//库函数
	}
	//返回长度的平方
	double len2(){
		return x*x + y*y;
	}
	//返回两点的距离
	double distance(Point p){
		return hypot(x-p.x,y-p.y);
	}
	Point operator +(const Point &b)const{
		return Point(x+b.x,y+b.y);
	}
	Point operator *(const double &k)const{
		return Point(x*k,y*k);
	}
	Point operator /(const double &k)const{
		return Point(x/k,y/k);
	}
	//`计算pa  和  pb 的夹角`
	//`就是求这个点看a,b 所成的夹角`
	//`测试 LightOJ1203`
	double rad(Point a,Point b){
		Point p = *this;
		return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) ));
	}
	//`化为长度为r的向量`
	Point trunc(double r){
		double l = len();
		if(!sgn(l))return *this;
		r /= l;
		return Point(x*r,y*r);
	}
	//`逆时针旋转90度`
	Point rotleft(){
		return Point(-y,x);
	}
	//`顺时针旋转90度`
	Point rotright(){
		return Point(y,-x);
	}
	//`绕着p点逆时针旋转angle`
	Point rotate(Point p,double angle){
		Point v = (*this) - p;
		double c = cos(angle), s = sin(angle);
		return Point(p.x + v.x*c - v.y*s,p.y + v.x*s + v.y*c);
	}
};
 
struct Line{
	Point s,e;
	Line(){}
	Line(Point _s,Point _e){
		s = _s;
		e = _e;
	}
	bool operator ==(Line v){
		return (s == v.s)&&(e == v.e);
	}
	//`根据一个点和倾斜角angle确定直线,0<=angle<pi`
	Line(Point p,double angle){
		s = p;
		if(sgn(angle-pi/2) == 0){
			e = (s + Point(0,1));
		}
		else{
			e = (s + Point(1,tan(angle)));
		}
	}
	//ax+by+c=0
	Line(double a,double b,double c){
		if(sgn(a) == 0){
			s = Point(0,-c/b);
			e = Point(1,-c/b);
		}
		else if(sgn(b) == 0){
			s = Point(-c/a,0);
			e = Point(-c/a,1);
		}
		else{
			s = Point(0,-c/b);
			e = Point(1,(-c-a)/b);
		}
	}
	void input(){
		s.input();
		e.input();
	}
	void adjust(){
		if(e < s)swap(s,e);
	}
	//求线段长度
	double length(){
		return s.distance(e);
	}
	//`返回直线倾斜角 0<=angle<pi`
	double angle(){
		double k = atan2(e.y-s.y,e.x-s.x);
		if(sgn(k) < 0)k += pi;
		if(sgn(k-pi) == 0)k -= pi;
		return k;
	}
	//`点和直线关系`
	//`1  在左侧`
	//`2  在右侧`
	//`3  在直线上`
	int relation(Point p){
		int c = sgn((p-s)^(e-s));
		if(c < 0)return 1;
		else if(c > 0)return 2;
		else return 3;
	}
	// 点在线段上的判断
	bool pointonseg(Point p){
		return sgn((p-s)^(e-s)) == 0 && sgn((p-s)*(p-e)) <= 0;
	}
	//`两向量平行(对应直线平行或重合)`
	bool parallel(Line v){
		return sgn((e-s)^(v.e-v.s)) == 0;
	}
	//`两线段相交判断`
	//`2 规范相交`
	//`1 非规范相交`
	//`0 不相交`
	int segcrossseg(Line v){
		int d1 = sgn((e-s)^(v.s-s));
		int d2 = sgn((e-s)^(v.e-s));
		int d3 = sgn((v.e-v.s)^(s-v.s));
		int d4 = sgn((v.e-v.s)^(e-v.s));
		if( (d1^d2)==-2 && (d3^d4)==-2 )return 2;
		return (d1==0 && sgn((v.s-s)*(v.s-e))<=0) ||
			(d2==0 && sgn((v.e-s)*(v.e-e))<=0) ||
			(d3==0 && sgn((s-v.s)*(s-v.e))<=0) ||
			(d4==0 && sgn((e-v.s)*(e-v.e))<=0);
	}
	//`直线和线段相交判断`
	//`-*this line   -v seg`
	//`2 规范相交`
	//`1 非规范相交`
	//`0 不相交`
	int linecrossseg(Line v){
		int d1 = sgn((e-s)^(v.s-s));
		int d2 = sgn((e-s)^(v.e-s));
		if((d1^d2)==-2) return 2;
		return (d1==0||d2==0);
	}
	//`两直线关系`
	//`0 平行`
	//`1 重合`
	//`2 相交`
	int linecrossline(Line v){
		if((*this).parallel(v))
			return v.relation(s)==3;
		return 2;
	}
	//`求两直线的交点`
	//`要保证两直线不平行或重合`
	Point crosspoint(Line v){
		double a1 = (v.e-v.s)^(s-v.s);
		double a2 = (v.e-v.s)^(e-v.s);
		return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
	}
	//点到直线的距离
	double dispointtoline(Point p){
		return fabs((p-s)^(e-s))/length();
	}
	//点到线段的距离
	double dispointtoseg(Point p){
		if(sgn((p-s)*(e-s))<0 || sgn((p-e)*(s-e))<0)
			return min(p.distance(s),p.distance(e));
		return dispointtoline(p);
	}
	//`返回线段到线段的距离`
	//`前提是两线段不相交，相交距离就是0了`
	double dissegtoseg(Line v){
		return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e)));
	}
	//`返回点p在直线上的投影`
	Point lineprog(Point p){
		return s + ( ((e-s)*((e-s)*(p-s)))/((e-s).len2()) );
	}
	//`返回点p关于直线的对称点`
	Point symmetrypoint(Point p){
		Point q = lineprog(p);
		return Point(2*q.x-p.x,2*q.y-p.y);
	}
};
 
 
int n;
int H;
Point a[maxn];
double ang[maxn];
int main() {
    scanf("%d%d",&n,&H);
    for (int i = 1; i <= n; i++) {
        a[i].input();
    }
    Point p(a[n].x, a[n].y + H);
    for (int i = 1; i <= n; i++) {
        ang[i] = p.rad(a[n], a[i]);
    }
 
    int pre = n;
    double ans = 0.0;
    for (int i = n-1; i >= 1; i--) {
        Line s(p, a[pre]);  // (s, pre)
        Line t(p, a[i]);
        if (s.parallel(t)) {
            if (pre-i == 1) {
                ans += a[i].distance(a[pre]);
            }
            pre = i;
        }
        else if (ang[i] > ang[pre]) {
            Line l(a[i], a[i+1]);  // (i, i+1)
            Point c = l.crosspoint(s);
            ans += c.distance(a[i]);
            pre = i;
        } 
    }
    printf("%.15lf\n", ans);
}

H. K and Medians

题意

给定一个数组，包含 $n$ 个数字 $1, 2, …, n$。

给定一个奇数 $k$，每次操作中，可以选择array中一个大小为 $k$ 的subsequence（不一定连续），保留median，remove掉其他的数字。

问是否可以通过这样的操作，使得最后留下 $m$ 个数，分别为 $b_1, b_2, … b_m$？

其中，$n \in [3, 2 \times 10^5], 3 \leq k \leq n, 1 \leq m < n, 1 \leq b_1 < b_2 … < b_m \leq n$。

题解

脑洞题。

我们首先给出结论：

设 $k = 2a + 1$，

如果我们只考虑所有要最终被remove掉的数，那么如果存在 $i$，使得 $b_i$ 的左边有 $\geq a$ 个要被remove的数，右边也有 $\geq a$ 个要被remove的数，并且 $(n-m)$ 可以被 $(2a)$ 整除，那么答案为 YES，否则为 NO。

这是充要条件，接下来证明：

• $(n-m)$ 可以被 $(2a)$ 整除是一个显然的条件，在接下来的证明中直接忽略。

存在 $i$，使得 $b_i$ 的左边有 $\geq a$ 个要被remove的数，右边也有 $\geq a$ 个要被remove的数 $\rightarrow$ 有解。

WLOG 我们设左边的数的数量 $\leq$ 右边。

我们一直移除右边，使得右边剩余数字数量 $< 2a$。

此时，左边 $\geq a$，右边 $< 2a$。

并且我们注意到，之前已经有 $(n-m)$ 可以被 $(2a)$ 整除这个条件了，说明我们需要移除偶数个数字，这说明左边需要移除的数字 + 右边需要移除的数字总量是一个偶数。

这说明，左右奇偶性 相同，又因为我们每次移除 $2a$ 个数字，并且左右两边相差不超过 $a-1$，这说明一定可以有一种移除方法使得左右平衡。

这意味着一定存在这样的remove方案。

• 注意到，在以上证明中，我们没有讨论每次 remove 选择的中位数是什么，因为这并不重要，只要保证在remove的过程中，不会动到那些需要保留的数字即可。

有解 $\rightarrow$ 存在 $i$，使得 $b_i$ 的左边有 $\geq a$ 个要被remove的数，右边也有 $\geq a$ 个要被remove的数。

假设不存在这样的 $i$，说明每次 remove 时，任何需要保留的数字都不能作为中位数。这意味着每次 remove 操作会选择一个最终需要扔掉的数字作为中位数，所以不可能remove干净。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;

int n, k, m, a[maxn];
int pre[maxn], suf[maxn];
bool solve() {
    if ((n - m) % (k-1)) return 0;
    for (int i = 1; i <= n; i++) {
        pre[i] = pre[i-1] + a[i];
    }
    for (int i = n; i >= 1; i--) {
        suf[i] = suf[i+1] + a[i];
    }
    for (int i = 1; i <= n; i++) {
        if (!a[i] && pre[i] >= k/2 && suf[i] >= k/2) return 1;
    }
    return 0;
}
int main() {
    int T; cin >> T;
    while (T--) {
        cin >> n >> k >> m;
        for (int i = 1; i <= n; i++) a[i] = 1, pre[i] = suf[i] = 0;
        for (int i = 1; i <= m; i++) {
            int x; cin >> x;
            a[x] = 0;
        }
        bool res = solve();
        if (res) cout << "YES\n";
        else cout << "NO\n";
    }
}

M. Similar Sets

题意

给定 $n$ 个set，一个set内部所有的正整数互不相同。

求是否存在 $2$ 个 set，使得这两个set中拥有至少 $2$ 个相同元素？如果有，输出这两个 set 的index，否则输出 $-1$。

其中，$n \leq 10^5$，并且所有set内的元素总数量 $\leq 2 \times 10^5$，所有元素 $\in [1, 10^9]$。

题解

分块讨论。将 size 大于 $\sqrt n$ 的看作大set，其余看作小 set。

那么有 $3$ 种情况：

大大
大小
小小

对于前两种情况：考虑到大set最多只有 $\sqrt n$ 个，那么只要对于每一个大的set，都维护一个 vis[] 代表这个set里有哪些元素，vis[x] = 1 代表 x 在这个大set内，然后对比其他所有set，判断其他所有set里是否有两个元素使得 vis[x] = 1 成立两次即可。

复杂度：设总共有 $m$ 个元素，那么复杂度为 $O(m\sqrt n)$。

对于第三种情况：

因为每个set都很小，小于 $\sqrt n$，所以对于每个 set 可以考虑处理出所有 pair $(u,v)$，其中 $u < v$，然后判断这个pair是否在其他的小set里。

但这样复杂度太高了，我们有个更优雅的写法：

从小到大枚举所有可能的 $v$，然后枚举这个 $v$ 所在的所有小set（可以预处理得出），在这些小set中枚举所有可能的比 $v$ 小的 $u$，然后判断这个 $u$ 之前是否也出现在另外一个小set中，并且这个小set还包含了 $v$。在代码中，用 last[u] = v, pos[u] = i 很优雅的实现了。

• 本质上来说，对于所有的 $v$，维护了一个list of 所有的 $u$，然后判断在这个list中是否存在两个相同的元素。

复杂度：$O(m\sqrt n)$。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;

int T, n;
vector<int> a[maxn];
int sz[maxn];
vector<int> big, small;

bool done = 0;
bool vis[maxn];
void solve_big() {
    for (int i : big) {
        for (int x : a[i]) vis[x] = 1;
        for (int j = 1; j <= n; j++) {
            if (j == i) continue;
            int cnt = 0;
            for (int x : a[j]) {
                if (vis[x]) cnt++;
            }
            if (cnt >= 2) {
                done = 1;
                printf("%d %d\n", i, j);
                return;
            }
        }
        for (int x : a[i]) vis[x] = 0;
    }
}


int last[maxn], pos[maxn];
set<int> small_num;  // 储存所有 small 里面的数字
vector<int> p[maxn];  // p[v]: 这个值所在的所有 small set 的index
void solve_small() {
    for (int v : small_num) {
        for (int i : p[v]) {
            for (int j = 0; j < a[i].size() && a[i][j] < v; j++) {
                int u = a[i][j];
                if (last[u] == v) {
                    done = 1;
                    printf("%d %d\n", i, pos[u]);
                    return;
                } else {
                    last[u] = v;
                    pos[u] = i;
                }
            }
        }
    }
}

map<int, int> id;
int cnt = 0;
void clearall() {
    for (int i = 1; i <= n; i++) {
        for (int j : a[i]) vis[j] = 0, p[j].clear(), last[j] = pos[j] = 0;
    }
    for (int i = 1; i <= n; i++) {
        sz[i] = 0;
        a[i].clear();
    }
    big.clear();
    small.clear();
    small_num.clear();
    done = 0;
    id.clear();
    cnt = 0;
}

const int M = 400;
int main() {
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &sz[i]);
            for (int j = 1; j <= sz[i]; j++) {
                int x; scanf("%d", &x);
                if (!id.count(x)) {
                    id[x] = ++cnt;
                } 
                a[i].push_back(id[x]);
            }
            sort(a[i].begin(), a[i].end());
            if (sz[i] > M) big.push_back(i);
            else small.push_back(i);
        }
        for (int i : small) {
            for (int j : a[i]) {
                small_num.insert(j), p[j].push_back(i);
            }
        }

        // 先处理 big
        solve_big();
        if (!done) {
            solve_small();
        }
        if (!done) printf("-1\n");

        clearall();
    }
}

Contents

G. Hobbits

H. K and Medians

M. Similar Sets