COMPFEST13

B. Building an Amusement Park

题意

二维平面上给定 $n$ 个点，求一个最小的圆，使得：

$(0,0)$ 在圆上。
圆内（包括圆上）包含至少 $k$ 个点。

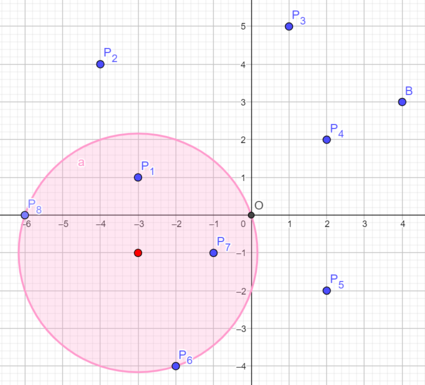
输出最小圆半径。

其中，$1 \leq n \leq 10^5, 1 \leq k \leq n, |x_i|, |y_i| \in [0, 10^5]$。

相对误差 $\leq 10^{-4}$。

题解

首先二分半径 $r$，

我们已知一个半径 $r$，已知圆需要过原点 $(0,0)$，那么我们只需要再确定圆上的一个点即可得到一个圆。

显然，想让半径最小，那么我们应该在此时恰好包括了一个点 $p_i$，这意味着只要枚举圆上的点 $p_i$ 即可确认 $n$ 个圆，只要判断这 $n$ 个圆中是否存在一个使得它包含了至少 $k$ 个点即可。

然而直接判断复杂度太高了，我们换种思考方式：

因为对于每个点 $p_i$，能够恰好让 $p_i$ 在圆上的圆有 $2$ 个，如果我们是逆时针旋转这个圆，那么恰好有 $2$ 个角度，使得这个圆恰好让这个点 $p_i$ 进来/出来。

所以如果圆心恰好在这两个角度 $a_1, a_2$ 之间，即圆心的极角在 $[a_1,a_2]$ 之间，说明这个点被包含进去了。

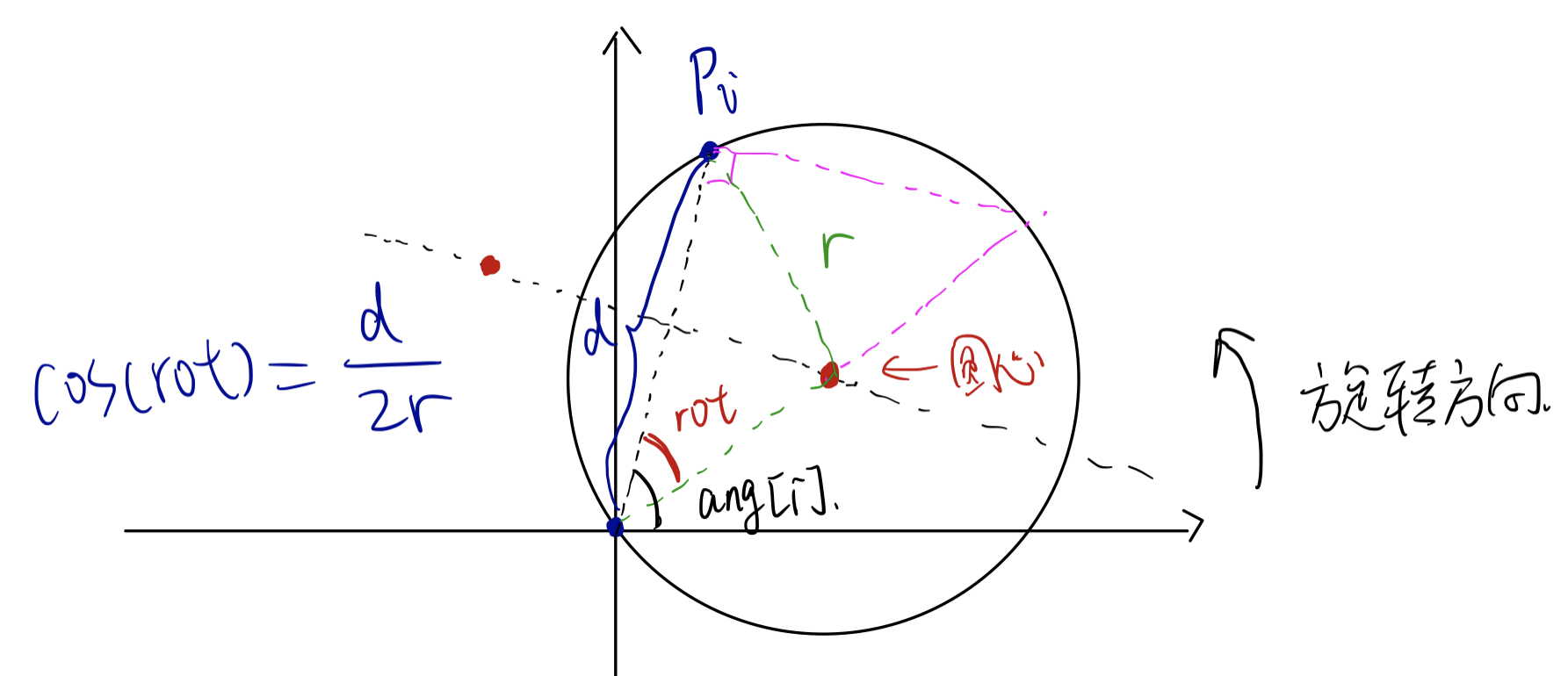
这个圆心的极角怎么计算呢？

可以先计算出每个点 $p_i$ 的极角 ang[i] 和距离圆心的距离 $d$，然后计算点 $p_i$ 与圆心的极角差 rot，可以得到 $\cos(rot) = \frac{d}{2r}$，这样就可以得到两个圆心的极角了。

剩下的就相当于一个区间覆盖问题了，可以直接 sort() 一下然后从左往右枚举，过程中维护当前覆盖点数（有优雅的写法连差分数组都不需要）。

更优雅的是，可以直接给所有的点加上 $2\pi$ 这样可以断环成链，剩下的完全一致，具体操作看代码吧。

• 最后注意特判一下某些点可能位于 $(0,0)$。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
int sgn(double x){
	if(fabs(x) < eps)return 0;
	if(x < 0)return -1;
	else return 1;
}
//square of a double
inline double sqr(double x){return x*x;}

struct Point{
	double x,y;
	Point(){}
	Point(double _x,double _y){
		x = _x;
		y = _y;
	}
	void input(){
		scanf("%lf%lf",&x,&y);
	}
	void output(){
		printf("%.2f %.2f\n",x,y);
	}
	bool operator == (Point b)const{
		return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
	}
	bool operator < (Point b)const{
		return sgn(x-b.x)== 0?sgn(y-b.y)<0:x<b.x;
	}
	Point operator -(const Point &b)const{
		return Point(x-b.x,y-b.y);
	}
	//叉积
	double operator ^(const Point &b)const{
		return x*b.y - y*b.x;
	}
	//点积
	double operator *(const Point &b)const{
		return x*b.x + y*b.y;
	}
	//返回长度
	double len(){
		return hypot(x,y);//库函数
	}
	//返回长度的平方
	double len2(){
		return x*x + y*y;
	}
	//返回两点的距离
	double distance(Point p){
		return hypot(x-p.x,y-p.y);
	}
	Point operator +(const Point &b)const{
		return Point(x+b.x,y+b.y);
	}
	Point operator *(const double &k)const{
		return Point(x*k,y*k);
	}
	Point operator /(const double &k)const{
		return Point(x/k,y/k);
	}
	//`计算pa  和  pb 的夹角`
	//`就是求这个点看a,b 所成的夹角`
	//`测试 LightOJ1203`
	double rad(Point a,Point b){
		Point p = *this;
		return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) ));
	}
	//`化为长度为r的向量`
	Point trunc(double r){
		double l = len();
		if(!sgn(l))return *this;
		r /= l;
		return Point(x*r,y*r);
	}
};


int n, k;
vector<pair<double, int>> vec;
long double dis[maxn], ang[maxn];
Point p[maxn];
bool check(long double x) {
    int cur = 0;
    vec.clear();
    for (int i = 1; i <= n; i++) {
        if (dis[i] > 0 && dis[i] <= 2.0*x) {
            double rot = acos(dis[i] / 2.0 / x);
            vec.push_back({ang[i] - rot, 1});  // 直接利用 +1, -1 来完成区间覆盖操作
            vec.push_back({ang[i] + rot, -1});
            vec.push_back({ang[i] - rot + 2 * pi, 1});   // 直接加上 2pi
            vec.push_back({ang[i] + rot + 2 * pi, -1});
        }
    }
    sort(vec.begin(), vec.end());  // -1 在前所以没问题
    for (auto di : vec) {
        cur += di.second;
        if (cur >= k) return 1;
    }

    return 0;
}


long double ans = 0.0;
int main() {
    scanf("%d%d", &n,&k);
    for (int i = 1; i <= n; i++) {
        p[i].input();
        if (abs(p[i].x) < eps && abs(p[i].y) < eps) k--;
        else {
            dis[i] = p[i].len();
            ang[i] = atan2(p[i].y, p[i].x);
        }
    }
    if (k <= 0) {
        ans = 0;
        printf("%.15Lf\n", ans);
        return 0;
    }

    long double low = 0.0, high = 2e5;
    int T = 100;
    while (high - low > 1e-6 && T--) {
        long double mid = (high + low) * 0.5;
        if (check(mid)) {
            ans = mid;
            high = mid;
        } else low = mid;
    }
    printf("%.15Lf\n", ans);
}

L. Longest Array Deconstruction

题意

给定 $n$ 个正整数 $a_i$，我们可以从中remove掉若干个元素，求remove后，最多有多少个 $i$ 满足 $a_i = i$？

其中，$n \leq 2 \times 10^5, a_i \in [1, 2 \times 10^5]$。

题解

先处理 $b_i = i - a_i$，如果 $b_i < 0$ 这意味着这个数字不可能对答案有贡献。

如果 $i > j$ 并且 $i - a_i \geq j - a_j$，那么就有办法通过 remove $(j, i)$ 中的一些元素来让 $i$ 满足条件。

• 一个特例是 $1, 1, 1$，这里 i[] = [1, 2, 3], a[] = [1, 1, 1], b[] = [0, 1, 2]，但是答案只能是 $1$，所以还得加个限制条件代表每个数只能被用一次。

所以我们需要找一个最长的 subsequence 使得序列中均为 index，并且转移时保证：

$j - a_j \leq i - a_i$。
$a_j < a_i$。
$j < i$。

看样子是个三维偏序，但实际上知道 $1,2$ 就可以推出 $3$，所以是二维偏序。

做二维偏序的方法：先根据一个维度 sort 一下，然后按照这个顺序加入元素，用线段树维护另外一个维度（另外一个维度的值作为 index），线段树里的值是转移的 dp值。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;

int n;
struct Node {
    int a, b, i;  // a : a[i], b : i - a[i], i : idx
} arr[maxn];  
int tr[maxn<<2];
void push_up(int cur) {
    tr[cur] = max(tr[cur<<1], tr[cur<<1|1]);
}

// 给位置 p 赋值为 x
void update(int cur, int l, int r, int p, int x) {
    tr[cur] = max(tr[cur], x);
    if (l == r) return;
    int mid = (l+r) >> 1;
    if (p <= mid) update(cur<<1, l, mid, p, x);
    else update(cur<<1|1, mid+1, r, p, x);
}

int query(int cur, int l, int r, int L, int R) {
    if (L <= l && R >= r) return tr[cur];
    int mid = (l+r) >> 1;
    int res = 0;
    if (L <= mid) res = max(res, query(cur<<1, l, mid, L, R));
    if (R > mid) res = max(res, query(cur<<1|1, mid+1, r, L, R));
    return res;
}

int main() {
    fastio;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> arr[i].a;
        arr[i].b = i - arr[i].a;
        arr[i].i = i;
    }
    sort(arr+1, arr+n+1, [](auto a, auto b) {
        if (a.b == b.b) return a.a < b.a;
        return a.b < b.b;
    });
    int N = 2e5;
    for (int i = 1; i <= n; i++) {
        int res = 0;
        if (arr[i].a - 1 > 0)
            res = query(1, 1, N, 1, arr[i].a - 1);
        
        if (arr[i].b >= 0)
            update(1, 1, N, arr[i].a, res + 1);
    }
    int ans = query(1, 1, N, 1, N);
    cout << ans << endl;
}

Contents

B. Building an Amusement Park

L. Longest Array Deconstruction