2021 NERC

CF1666J Job Lookup

题意

给定一个 $n \times n$ 的矩阵 $c_{i j}$ 。

求一个BST，使得 $\sum_{i, j} c_{i j} \cdot d_{i j}$ 最小。

其中， $d_{i j}$ 代表节点 $i, j$ 在BST中的距离。

输出这个 BST 的结构。

其中， $n \leq 200$ ， $c_{i j} \in [0, 10^{9}], c_{i i} = 0$ 。

题解

注意 BST 一个非常重要的结论：

子树内的节点编号是一个连续的区间。

所以可以考虑用区间DP来做。

设 $d p (i, j)$ 为 $[i, j]$ 之间形成的子树对应的最小值。

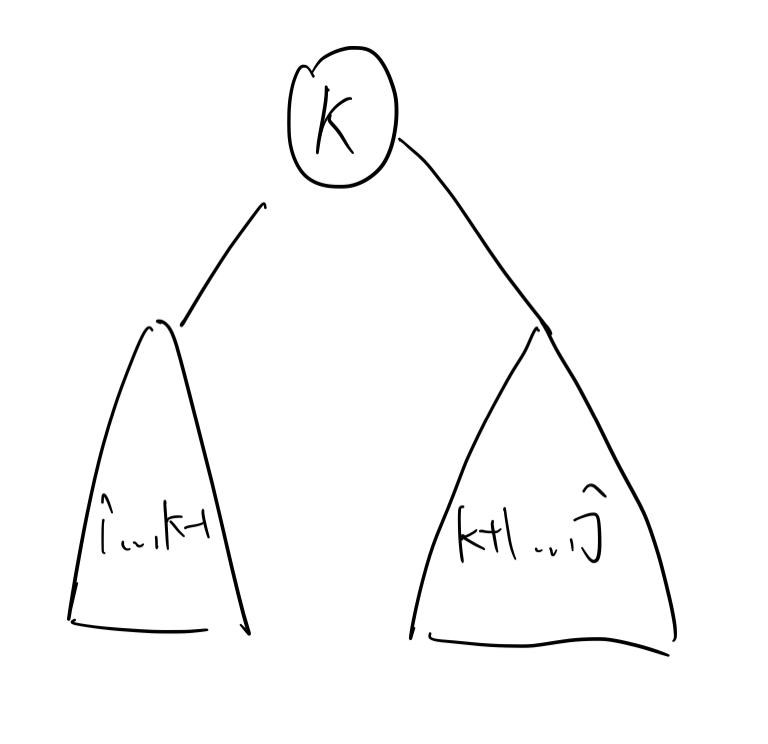
显然转移方程是枚举 parent节点 $k$ 。

而 $d_{i j}$ 可以考虑每条边带来的贡献，在这个转移过程中我们只需要考虑这两条边带来的贡献。

所以 $[i, k - 1]$ 给除了它本身以外的所有部分带来了贡献，贡献部分为：

$\sum_{a \in [i, k - 1]} \sum_{b \in [1, n]} c_{a b} - \sum_{a \in [i, k - 1]} \sum_{b \in [i, k - 1]} c_{a b}$

$[k + 1, j]$ 同理。

转移方程有：

$d p (i, j) = min_{k \in [i, j]} {d p (i, k - 1) + d p (k + 1, j) + \sum_{a \in [i, k - 1]} \sum_{b \in [1, n]} c_{a b} - \sum_{a \in [i, k - 1]} \sum_{b \in [i, k - 1]} c_{a b} + \sum_{a \in [k + 1, j]} \sum_{b \in [1, n]} c_{a b} - \sum_{a \in [k + 1, j]} \sum_{b \in [i, k - 1]} c_{a b}}$

用二维前缀和预处理一下即可。

代码

copy
#include <bits/stdc++.h>
using namespace std;
const int maxn = 205;
int n;
ll c[maxn][maxn];
ll sumc[maxn][maxn], dp[maxn][maxn];
int use[maxn][maxn];
int par[maxn];
ll sum_matrix(int xl, int xr, int yl, int yr) {
    if (xl > xr || yl > yr) return 0;
    return sumc[xr][yr] - sumc[xl-1][yr] - sumc[xr][yl-1] + sumc[xl-1][yl-1];
}
void dfs(int i, int j, int p) {
    if (i > j) return;
    if (i == j) {
        par[i] = p;
        return;
    }
    int k = use[i][j];
    par[k] = p;
    dfs(i, k-1, k);
    dfs(k+1, j, k);
}
ll DP(int i, int j) {
    if (i > j) return 0;
    if (dp[i][j] >= 0) return dp[i][j];
    dp[i][j] = 1e18;
    for (int k = i; k <= j; k++) {
        ll res = DP(i, k-1) + DP(k+1, j);
        res += sum_matrix(i, k-1, 1, n) - sum_matrix(i, k-1, i, k-1);
        res += sum_matrix(k+1, j, 1, n) - sum_matrix(k+1, j, k+1, j);
        if (res < dp[i][j]) {
            dp[i][j] = res;
            use[i][j] = k;
        }
    }
    return dp[i][j];
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) cin >> c[i][j];
    }
    memset(dp, -1, sizeof(dp));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            sumc[i][j] = sumc[i-1][j] + sumc[i][j-1] - sumc[i-1][j-1] + c[i][j];
        }
    }
    DP(1, n);
    dfs(1, n, 0);
    for (int i = 1; i <= n; i++) cout << par[i] << " ";
    cout << endl;
}

CF1666E Even Split

题意

给定一个长度为 $L$ 的直线，现在直线上有 $n$ 个位置互不相同的点。

求一种方案，将这个直线分成 $n$ 段，并且保证第 $i$ 个点属于第 $i$ 条线段（包括边界），线段之间没有空隙，并且第 $1$ 个线段的左端一定是 $0$ ，第 $n$ 个线段的右端一定是 $L$ 。

• 相当于划定 $n - 1$ 个分割点，将直线分成 $n$ 段。

求一种分割方案，使得这些线段中，最长的与最短的差距最小？

其中， $n \leq 10^{5}, L \leq 10^{9}$ 。

题解

首先易知可以二分最终的长度差。

然后我们需要确定一个线段的长度范围 [ml, mr]，注意到这个范围也是可以二分的（为什么？）。

所以我们二分 $m l$ 的值。

那么给定 [ml, mr] 这个范围区间，怎么check是否合法？

我们从左向右，考虑第 $i$ 个区间的右端点可能的范围。

copy
int check(int mn, int mx) {
    l[0] = 0, r[0] = 0;
    int c = 0;
    for (int i = 1; i <= n; i++) {
        if (l[i-1] + mn > p[i+1]) return -1;  // mn 太大了
        if (r[i-1] + mx < p[i]) return 1;  // mn 太小了
        // [l,r] 表示右端点可能在的区间 
        l[i] = max(l[i-1] + mn, p[i]);
        r[i] = min(r[i-1] + mx, p[i+1]);
    }
    if (l[n] > L) return -1;
    if (r[n] < L) return 1;
    return 0;  // ok
}

我们让 $l$ 表示这个右端点尽可能的小， $r$ 表示尽可能大。

然后判断这个范围是否一直合法即可。

如果不合法，也可以通过不合法的是哪个条件推测出 $m l$ 的值是大了还是小了，从而返回不同的值。

现在我们求出了最优的范围区间 [ml, mr]，怎么得到最终的区间分配结果？

我们不能简单的取 $[l_{i}, r_{i}]$ 中的值，因为这个范围只是代表：

一定存在一种分配方案，使得第 $i$ 个区间的右端点落在了 $[l_{i}, r_{i}]$ 中，反之则不一定成立。

不过注意到，第 $n$ 个区间的右端点是已经确定为 $L$ 了的，所以我们从右向左构造答案，设 res[i] 为第 $i$ 个区间的右端点，那么只要保证 res[i-1] 与 res[i] 的距离在 [ml, mr] 之间，并且 res[i-1] $\in [l_{i}, r_{i}]$ 即可。由于前面的答案，这样的方案一定是存在的。

代码

copy
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
ll L;
int n;
int p[maxn];
int l[maxn], r[maxn];
int check(int mn, int mx) {
    l[0] = 0, r[0] = 0;
    int c = 0;
    for (int i = 1; i <= n; i++) {
        if (l[i-1] + mn > p[i+1]) return -1;  // mn 太大了
        if (r[i-1] + mx < p[i]) return 1;  // mn 太小了
        // [l,r] 表示右端点可能在的区间 
        l[i] = max(l[i-1] + mn, p[i]);
        r[i] = min(r[i-1] + mx, p[i+1]);
    }
    if (l[n] > L) return -1;
    if (r[n] < L) return 1;
    return 0;  // ok
}
int ml, mr;
bool check_diff(int d) {
    int low = 1, high = 1e9;
    while (low <= high) {
        int mid = (low + high) >> 1;
        int res = check(mid, mid+d);
        if (!res) {
            ml = mid, mr = mid+d;
            return 1;
        } else if (res == 1) {
            low = mid+1;
        } else high = mid-1;
    }
    return 0;
}
int res[maxn];  // res[i]: 第i个区间的右端点
int main() {
    cin >> L >> n;
    for (int i = 1; i <= n; i++) cin >> p[i];
    p[n+1] = L;
    int low = 0, high = 1e9, ans = 1e9;
    while (low <= high) {
        int mid = (low + high) >> 1;
        if (check_diff(mid)) {
            ans = mid;
            high = mid-1;
        } else low = mid+1;
    }
    check(ml, mr);  // 这里需要再check一下保证 l[] 和 r[] 里面的值正确
    res[n] = L;
    for (int i = n-1; i >= 1; i--) {
        int lmax = max(l[i], res[i+1] - mr), rmin = min(r[i], res[i+1] - ml);
        assert(lmax <= rmin);
        res[i] = lmax;
    }
    for (int i = 1; i <= n; i++) {
        cout << res[i-1] << " " << res[i] << "\n";
    }
}

Contents

CF1666J Job Lookup

CF1666E Even Split