树的重心 - tom0727's blog

定义

树的重心是指：

在一棵无权无根树中，对于每一个点 $u$ ，计算它所有子树中最大的子树的节点数，这个最大值最小的点 $u$ 就是树的重心。

性质

点 $u$ 为重心 $⟺$ 以 $u$ 为根时，所有子树大小 $\leq \frac{n}{2}$
重心至少有一个，最多有两个。

2.1. 如果有两个重心，那么它们之间一定有一条边相连，且此时树一定是有偶数个节点，且存在一种方式分割成两棵树，使得这两个重心分别为两棵树的重心。
点 $u$ 为重心 $⟺$ 树中所有点到某个点的距离和中，到 $u$ 的距离和是最小的。

3.1. 如果有两个重心，那么到它们的距离和一样。
把两棵树通过一条边相连得到一棵新的树，那么新的树的重心在连接原来两棵树的重心的路径上，并且新重心会落在较大的树那边。
在一棵树上添加或删除一个叶子，那么它的重心最多只移动一条边的距离。

证明

$\Rightarrow$ ：如果存在一个重心使得某个子树大小 $> \frac{n}{2}$ ，那么向着这个子树的方向移动一条边，一定能找到一个更优的重心。 $\Leftarrow$ ：当以 $u$ 为根时，如果所有子树大小 $\leq \frac{n}{2}$ ，那么它的任意邻居 $v$ 不可能比 $u$ 更优，因为以 $v$ 为根时， $u$ 所在子树的大小会 $\geq \frac{n}{2}$ 。
易证一个和两个的情况，如果有 $3$ 个重心，易证每两个重心之间一定有一条边相连，而这样的话会形成一个大小为 $3$ 的环，不可能是树。

2.1. 有两个重心意味着有两个大小为 $\frac{n}{2}$ 的子树。
设点 $u$ 到所有其他点的距离为 $d_{u}$ ，那么如果存在一个邻居 $v$ 使得 $v$ 所在子树的大小 $> \frac{n}{2}$ ，那么移动到 $v$ 一定有 $d_{v} < d_{u}$ （因为贡献的点数量 $> \frac{n}{2}$ ）。由此可以推出，除了重心以外的点都至少存在一个邻居使得 $d_{v}$ 更小，可以得出重心的 $d_{u}$ 最小。
WLOG 假设两棵树一大一小，可以看作将小子树一个个作为叶子的加入到大子树上，此时重心会沿着连接的点方向移动。
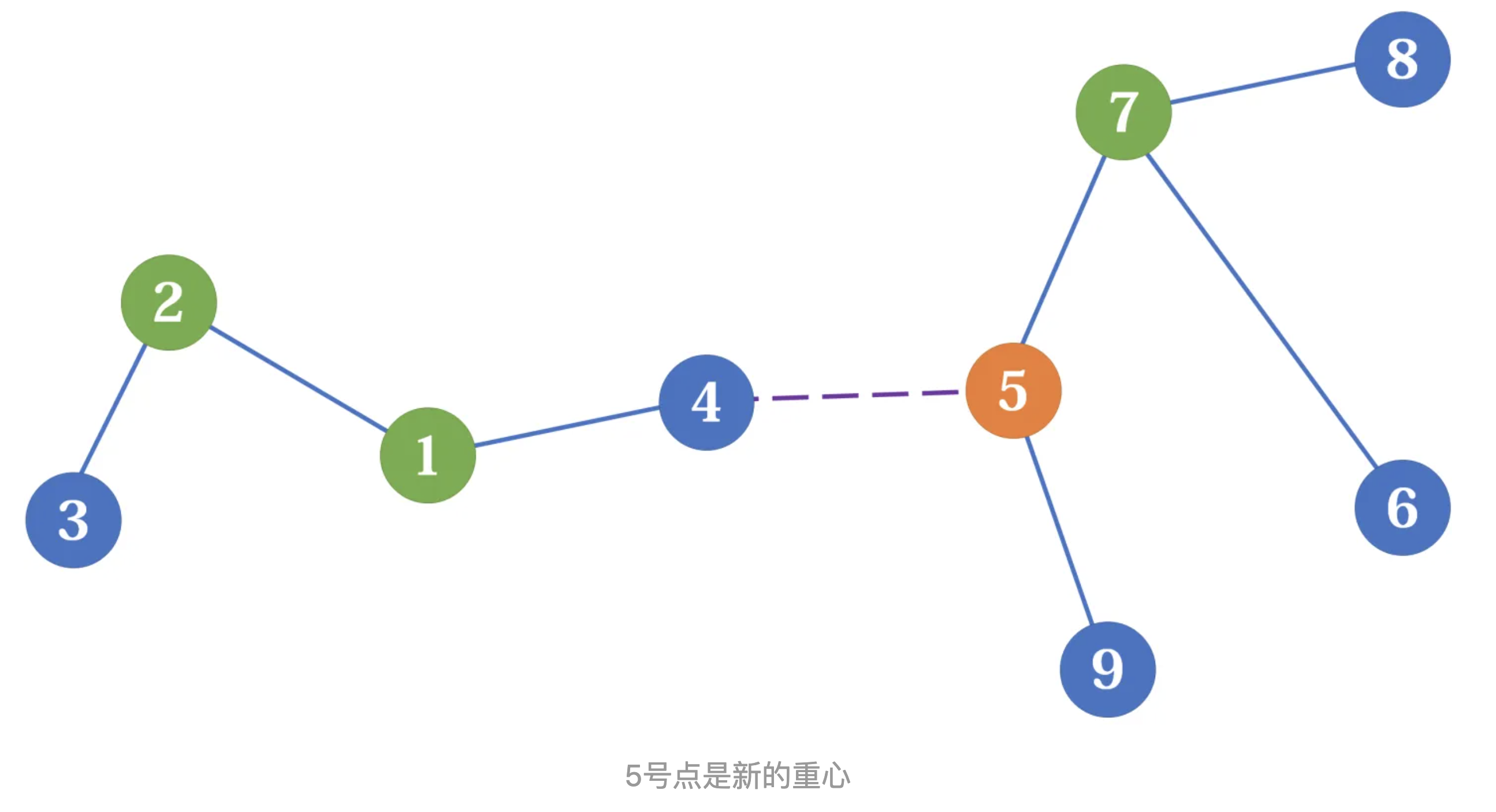
易证。

例题

例1 CF1406C. Link Cut Centroids

题意

给定一棵树，我们需要切掉一个edge，再加上一个edge，使得新生成的仍然是一棵树，并且仅有一个重心。

求出这样的方案，答案一定存在。

其中， $n \leq 10^{5}$ 。

题解

首先判断重心是不是有 $2$ 个，如果不是，什么也不用干。

如果是，那么设两个重心分别为 $c_{1}, c_{2}$ ，那么只要在 $c_{2}$ 子树中寻找一个叶子，然后切下来，安给 $c_{1}$ 即可。

证明：易证 $c_{1}$ 的其他邻居不可能为新的重心，而 $c_{2}$ 也不可能为重心，因为 $c_{2}$ 所在的部分少了一个，所以只有 $c_{1}$ 变成新的重心了。

代码

copy
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int T, n;
struct Edge {
    int from, to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v) {
    Edge e = {u, v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}
int sz[maxn];
bool center[maxn];
int c1, c2;
void dfs1(int u, int p) {
    sz[u] = 1;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int v = edges[e].to;
        if (v == p) continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (sz[v] > n/2) center[u] = 0;
    }
    if (n - sz[u] > n/2) center[u] = 0;
}
int c, cp;
// f: forbidden
void dfs2(int u, int p, int f) {
    sz[u] = 1;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int v = edges[e].to;
        if (v == f || v == p) continue;
        dfs2(v, u, f);
        sz[u] += sz[v];
    }
    if (sz[u] == 1) {
        c = u;
        cp = p;
    }
}
int main() {
    fastio;
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 1; i < n; i++) {
            int x,y; cin >> x >> y;
            addEdge(x, y); addEdge(y, x);
        }
        for (int i = 1; i <= n; i++) center[i] = 1;
        dfs1(1, 0);
        c1 = c2 = 0;
        for (int i = 1; i <= n; i++) {
            if (center[i]) {
                if (!c1) c1 = i;
                else c2 = i;
            }
        }
        if (!c2) {
            cout << edges[1].from << " " << edges[1].to << "\n" << edges[1].from << " " << edges[1].to << "\n";
        } else {
            c = cp = 0;
            dfs2(c2, 0, c1);
            cout << c << " " << cp << "\n" << c << " " << c1 << "\n";
        }
        for (int i = 1; i <= n; i++) head[i] = 0, sz[i] = 0;
        ecnt = 1;
    }
}

例2 CF685B. Kay and Snowflake

题意

给定一棵有根树（ $1$ 为根），和 $q$ 次询问，每次询问回答 $u$ 的子树中，重心是哪个点。

其中， $n, q \leq 3 \times 10^{5}$ 。

题解

结论：考虑 $u$ 的子树，它的重心要么是它自己，要么在它重儿子所在子树里。

如果在它重儿子（设为 $v$ ）里，那么可以看作以 $v$ 为子树，然后加上了一个较小的子树（ $u$ 剩下的部分），所以原本重心是 $v$ 的重心，加上了以后，重心会往连接点处移动，所以新的重心一定是 $v$ 的重心的 ancestor。

所以我们可以从下往上处理每个子树的重心，处理到 $u$ 时只要从它的重儿子 $v$ 的重心 $c_{v}$ 开始，暴力往上跳即可。

可证每个点最多会被跳 $1$ 次，复杂度为 $O (n)$ 。

代码

copy
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5;
int n, q;
struct Edge {
    int from, to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v) {
    Edge e = {u, v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}
int sz[maxn], par[maxn], son[maxn], maxsz[maxn], ans[maxn];
void dfs(int u, int p) {
    sz[u] = 1;
    par[u] = p;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int v = edges[e].to;
        if (v == p) continue;
        dfs(v, u);
        sz[u] += sz[v];
        if (maxsz[u] < sz[v]) {
            son[u] = v;
            maxsz[u] = sz[v];
        }
    }
}
void dfs2(int u, int p) {
    for (int e = head[u]; e; e = edges[e].nxt) {
        int v = edges[e].to;
        if (v == p) continue;
        dfs2(v, u);
    }
    if (maxsz[u] <= sz[u] / 2) {
        ans[u] = u;
        return;
    } else {
        int c = ans[son[u]];
        while (c != u) {
            if (maxsz[c] <= sz[u] / 2 && sz[u] - sz[c] <= sz[u] / 2) {
                ans[u] = c;
                break;
            } else c = par[c];
        }
    }
}
int main() {
    cin >> n >> q;
    for (int i = 2; i <= n; i++) {
        int p; cin >> p;
        addEdge(p, i);
        addEdge(i, p);
    }
    dfs(1, 0);
    dfs2(1, 0);
    while (q--) {
        int x; cin >> x; cout << ans[x] << "\n";
    }
}

参考链接

https://zhuanlan.zhihu.com/p/357938161

Contents

定义

性质

例题

例1 CF1406C. Link Cut Centroids

例2 CF685B. Kay and Snowflake

参考链接