2020-2021 ICPC NERC (NEERC), North-Western Russia Regional Contest
Contents
L. Lost Permutation
题意
交互题。
有一个隐藏的 permutation $\pi$,长度为 $n$。
现在只有一种询问:
$? ~f_1 ~f_2 … ~f_n$:给定一个 permutation $f$,系统会回答你一个 permutation $g$,其中 $g = \pi^{-1} \circ f \circ \pi$。
你只能询问 $2$ 次,回答这个隐藏的 permutation $\pi$。
其中,$3 \leq n \leq 10^4$。
Permutation 的定义
Permutation 的定义:
若有一个permutation $a=(4,1,3,2)$,我们需要看第 $i$ 位上的数字 $a_i$,意味着把旧 permutation 第 $i$ 位上的数字映射到新 permutation 中的第 $a_i$ 位。
• 这里 $a$ 是一个运算符,单独存在时,旧的permutation都是 $1,2,3,…,n$。
- $i = 1, a_1 = 4$,说明把第 $1$ 位的数字(是 $1$)放到 第 $4$ 位,所以新 permutation 就是 $(?, ?, ?, 1)$。
- $i = 2, a_2 = 1$,说明把第 $2$ 位的数字(是 $2$)放到 第 $1$ 位,所以新 permutation 就是 $(2, ?, ?, 1)$。
- $i = 3, a_3 = 3$,说明把第 $3$ 位的数字(是 $3$)放到 第 $3$ 位,所以新 permutation 就是 $(2, ?, 3, 1)$。
- $i = 4, a_4 = 2$,说明把第 $4$ 位的数字(是 $4$)放到 第 $2$ 位,所以新 permutation 就是 $(2, 4, 3, 1)$。
由此也可以得出 $a^{-1} = (2,4,3,1)$。
$a \circ b$ 则代表对于 $I=(1,2,3…,n)$ 先施加 $a$,再施加 $b$。
所以可得:
若 $a = (4,1,3,2), b = (3,2,1,4)$,那么 $a \circ b = (4,3,1,2)$。
题解
置换群。
首先明确 $\forall \pi, f, \pi^{-1} \circ f \circ \pi$ 与 $f$ 是共轭的(conjugate)。
这意味着,如果我们把一个 permutation 看作一个图:
例如 $b = (3,2,1,4)$,那么有 $1 \rightarrow 3, 2 \rightarrow 2, 3 \rightarrow 1, 4 \rightarrow 4$。
$a=(4,1,3,2),a^{-1} = (2,4,3,1)$
$a^{-1} \circ b \circ a = (1,2,4,3)$,所以有 $1 \rightarrow 1, 2 \rightarrow 2, 3 \rightarrow 4, 4 \rightarrow 3$。
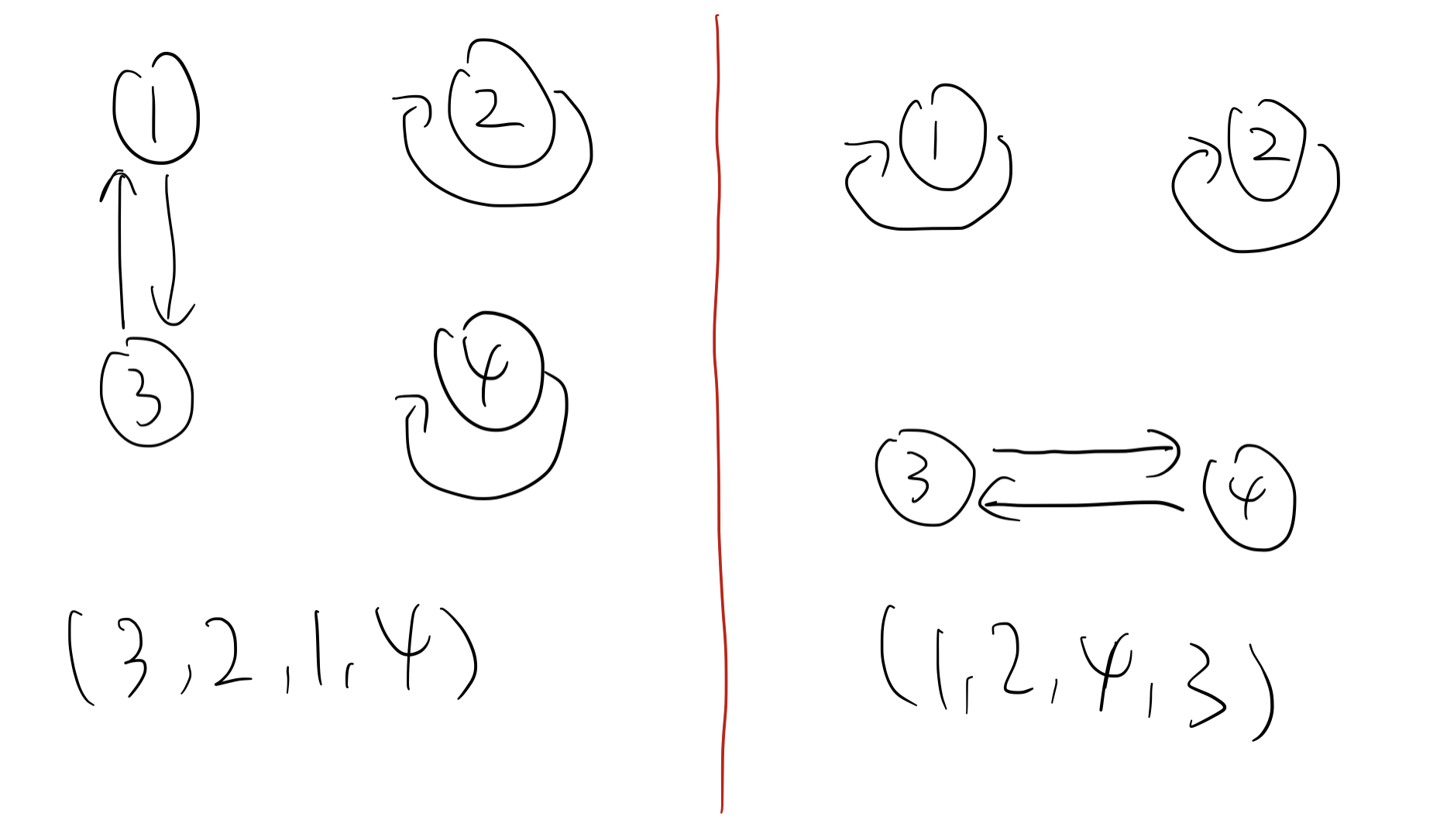
看到图上的结构是不是完全一致?由此,得出一个结论:
两个 permutation 是共轭的 $\iff$ 存在一种 bijection,使得图上节点重新编号,能得到另外一个图。
这也等价为下图:
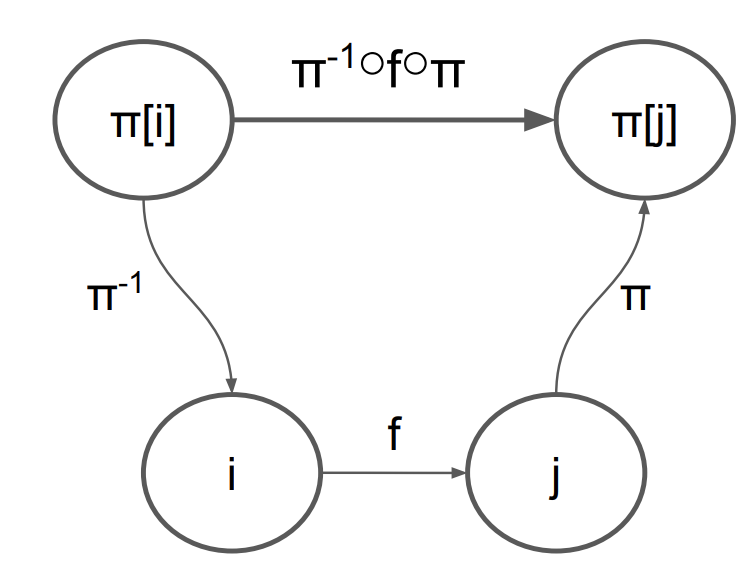
所以我们的方案就有了:
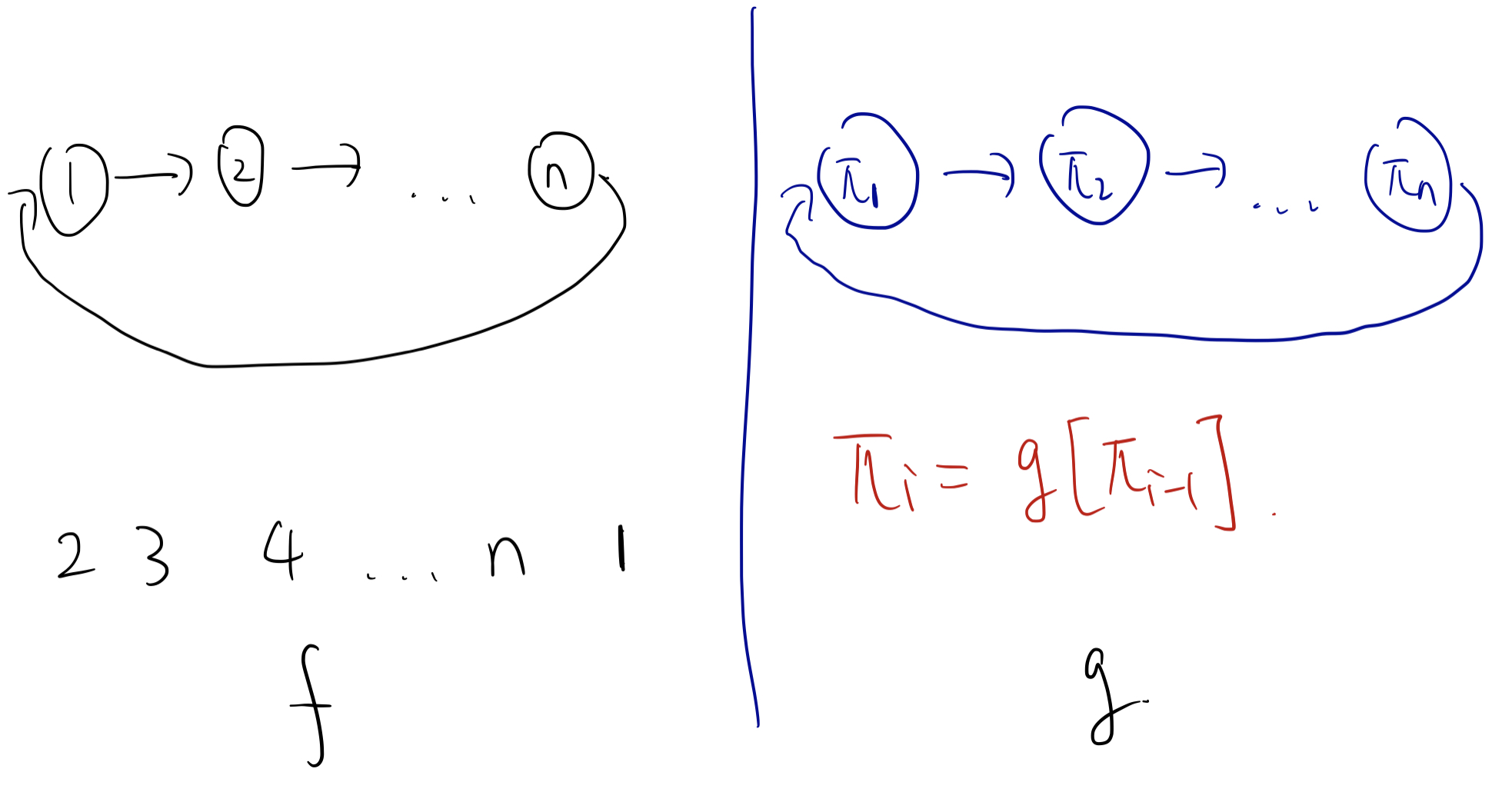
第一次询问 $f = (2,3,4,…,n,1)$,这样可以得到一个大的环,而返回的 $g$ 也一定是一个大环。
并且我们只要找到 $\pi_1$,剩下的都可以找到了。
第二次询问:
我们需要找到 $\pi_1$,利用共轭的特点,我们不妨询问一个 fixed point $1$ 和一个环。
所以第二次询问 $f = (1, 3, 4, …, n, 2)$,这样回答我们的也是一个 fixed point $\pi_1$ 和一个环,所以只要找到这个 fixed point 即可得到 $\pi_1$。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
int T;
int a[maxn], b[maxn], ans[maxn];
int main() {
cin >> T;
while (T--) {
int n; cin >> n;
cout << "? ";
for (int i = 2; i <= n; i++) cout << i << " ";
cout << 1 << "\n";
fflush(stdout);
for (int i = 1; i <= n; i++) cin >> a[i];
cout << "? ";
cout << 1 << " ";
for (int i = 3; i <= n; i++) cout << i << " ";
cout << 2 << "\n";
fflush(stdout);
int p;
for (int i = 1; i <= n; i++) {
cin >> b[i];
if (b[i] == i) p = i;
}
ans[1] = p;
for (int i = 2; i <= n; i++) ans[i] = a[ans[i-1]];
cout << "! ";
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << "\n";
fflush(stdout);
}
}
N. Nunchucks Shop
题意
现在有若干个棒子,每个棒子里包含 $n$ 个珠子(要么是白,要么是黑)。
每一种组合由两根棒子连接而成,并且总共包含 $k$ 个黑色珠子。
现在问需要多少个棒子,使得所有可能的组合都能出现?
例如:
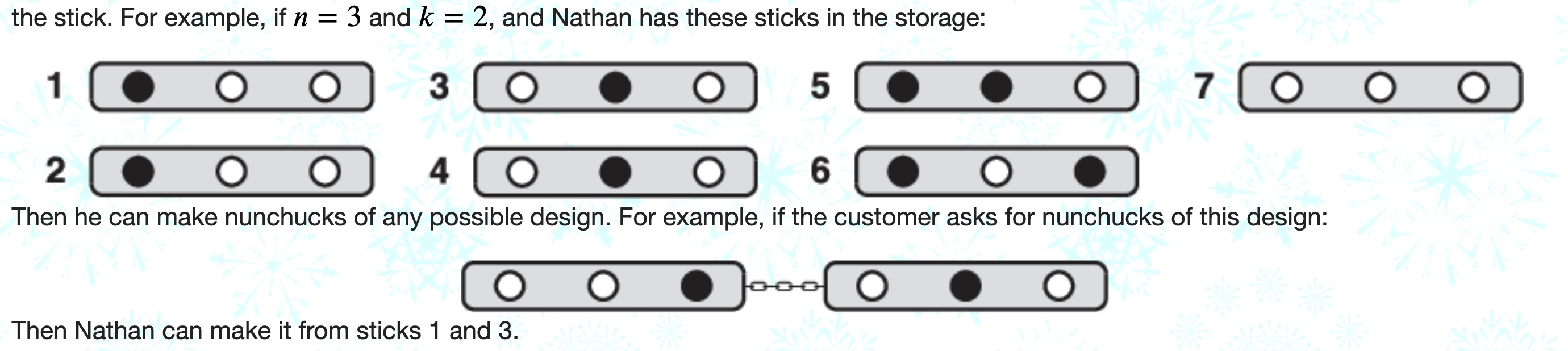
$n=3, k=2$ 时就需要 $7$ 个。
• 注意到棒子是可以左右翻转的,所以需要考虑对称的情况。
其中,$n \leq 50, k \in [0, 2n]$。
题解
如果 $k \geq n+1$,那么就让黑白颠倒,即 $k = 2n - k$。
所以只用考虑 $k \leq n$ 的情况。
那么两根棒子,黑色珠子的数量组合为 $(0,k), (1,k-1) … (k,0)$,其中对称的情况是一样的,即 $(0,k) = (k,0)$。
那么只要求出,一个棒子中,有 $j$ 个黑色珠子的话,有多少种情况即可(需要考虑对称)。
我们令这个值为 $S(n,j)$。
如果不考虑对称,很明显是 $C(n,j)$。
如果要考虑对称,我们设黑色为 $1$,白色为 $0$,那么 $1000$ 和 $0001$ 就是对称的,每当有两个不同的字符串对称时,数量就会减一。
但是也有些字符串的对称是自己(回文串):比如 $1111$ 对称的是 $1111$,$0110$ 对称的是 $0110$。
那么有多少种字符串是回文串?
如果 $n$ 是偶数,$k$ 是奇数,可以发现不存在回文串。
否则,有 $C(\frac{n}{2}, \frac{j}{2})$ 个回文串。
因为一个回文串如果左边部分定了,右边部分也定了,所以就相当于只能从 $\frac{n}{2}$ 个格子里选 $\frac{j}{2}$ 个黑色的。
于是有
$$S(n,j) = \frac{C(n,j) + C(\frac{n}{2}, \frac{j}{2})}{2}$$
而最终答案就是
$$ans = \sum\limits_{j=0}^k S(n,j)$$
当然还要加上 $S(n,\frac{k}{2})$,如果 $k$ 是偶数。
代码
#include <bits/stdc++.h>
using namespace std;
ll C[55][55];
ll cnt(int n, int k) {
if (n % 2 == 0 && k % 2 == 1) return C[n][k] / 2;
return (C[n][k] + C[n/2][k/2]) / 2;
}
int n, k;
int main() {
cin >> n >> k;
C[0][0] = 1;
for (int i = 1; i <= 50; i++) {
C[i][0] = 1;
for (int j = 1; j <= i; j++) {
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
if (k >= n+1) k = 2*n - k;
ll ans = 0;
for (int i = 0; i <= k; i++) {
int j = k - i;
if (i > j) break;
ans += cnt(n, i) + cnt(n, j);
}
cout << ans << "\n";
}
