容斥原理
Contents
介绍
容斥原理用于计算集合的 union 和 intersection 的大小。
集合的 Union:
$$|\bigcup_{i=1}^{n} S_i| = \sum_{i} |S_i| - \sum_{i < j} |S_i \cap S_j| + \sum_{i < j < k} |S_i \cap S_j \cap S_k| - … + (-1)^{n-1} |S_1 \cap … \cap S_n|$$
集合的 Intersection = 全集 - 补集的并集
$$|\bigcap_{i=1}^n S_i| = |U| - |\bigcup_{i=1}^n \bar S_i|$$
例题
例1 CF1425D. Danger of Mad Snakes
题意
一个 $1000 \times 1000$ 的矩阵里放了 $n$ 条蛇,第 $i$ 个蛇位于 $(x_i, y_i)$,价值 $b_i$。
现在,我们要放 $m$ 个炸弹,每个炸弹必须放在某条蛇身上(不能重叠)。炸弹会爆炸,爆炸半径为 $r$。
• 比如,炸弹放在 $(x,y)$ 处,那么所有 $\max(|x - x'|, |y - y'|) \leq r$ 的点 $(x’, y’)$ 都会受到影响。
每一个炸弹放置方案所带来的价值定义为:$(\sum\limits_{i} b_{i})^2$,其中 $i$ 是所有被炸弹炸到的蛇。
求所有炸弹放置方案的价值之和,答案对 $10^9+7$ 取模。
其中,$n \in [1, 2000], m \in [1, n], r \in [0, 1000), x_i, y_i \in [1, 1000], b_i \in [1, 10^6]$,蛇的位置互不相同。
题解
看见这种 所有方案 的和,就想到每一个元素所带来的贡献。
很明显总共有 $C_n^m$ 种方案,每种方案如果炸到的蛇是 $(a_1, a_2, …, a_k)$,那么价值就是
$$(\sum\limits_{i=1} b_{a_i})^2 = (b_{a_1} + b_{a_2} + … + b_{a_k})^2 = \sum\limits_{i=1}^k b_{a_i}^2 + \sum\limits_{i<j} 2b_{a_i}b_{a_j}$$
先看第一项 $\sum\limits_{i=1}^k b_{a_i}^2$,只要考虑:
对于每一条蛇,有多少种方案能炸到它?
这个不好算,不如考虑有多少种炸不到它。
我们可以预处理出炸弹放在每一条蛇,都能影响到哪些蛇。这样就可以得到有哪些蛇的位置放置炸弹,是炸不到这一条的。
假设有 $k$ 个位置放炸弹,炸不到它,那么能炸到它的方案数就是 $C_n^m - C_k^m$。
再看第二项 $\sum\limits_{i<j} 2b_{a_i}b_{a_j}$,我们要考虑:
对于每两条蛇 $(i,j)$,有多少种方案都能炸到它们?
我们设 $A$ 为第一条蛇被炸,$B$ 为第二条蛇被炸。
所以由容斥原理有:
$$|A \cap B| = |U| - |\bar A \cup \bar B| = |U| - |\bar A| - |\bar B| + |\bar A \cap \bar B|$$
易知 $|U| = C_n^m, 而 |\bar A|, |\bar B|$ 上面已经算出来了,就剩下 $|\bar A \cap \bar B|$。
这代表着两条蛇都没被炸,所以只要找出有哪些点,使得这两条蛇都不会被炸就行。
没法直接找,所以找有哪些点能分别炸到这两条蛇,然后取一个并集,用 $m$ 减掉这个并集的大小即可。
注意到,能炸到一条蛇的范围是一个正方形,所以我们就取这两个正方形的并集,也就是将两个正方形相加然后减去正方形的交集。
我们做一个 $01$ 矩阵,$1$ 代表这个位置可以放炸弹(有蛇),然后正方形的值就是这个正方形内的和,所以用二维前缀和。
正方形的交集怎么求?
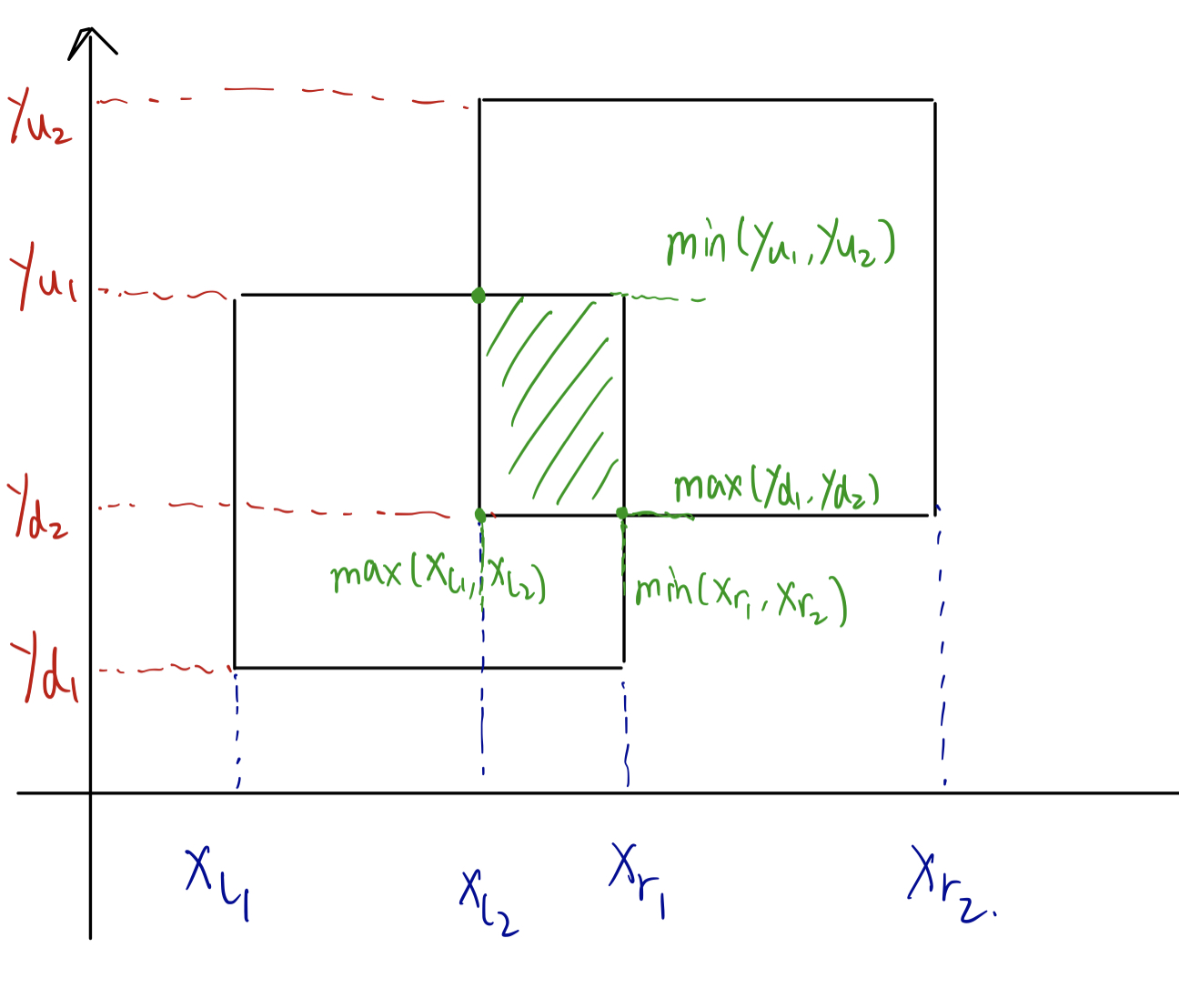
让两个正方形的:
- 左端点 $x$ 坐标取 $\max$,右端点 $x$ 坐标取 $\min$。
- 下端点 $y$ 坐标取 $\max$,上端点 $y$ 坐标取 $\min$。
然后就可以得出正方形的范围是 $[x_{lmax}, x_{rmin}] \times [y_{dmax}, y_{umin}]$。
• 当然这个题坐标系原点在左上方,所以稍微修改一下即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e4+5;
Z fac[maxn], inv_fac[maxn];
Z C(int a, int b) {
if (b > a) return 0;
return fac[a] * inv_fac[b] * inv_fac[a-b];
}
int n, m, r;
int x[maxn], y[maxn];
ll b[maxn];
vector<int> adj[maxn];
int sum[maxn/2][maxn/2];
Z ans = 0;
struct Point {
int x, y;
};
struct Matrix {
Point ul, ur, dl, dr; // upper left, upper right, down left, down right
} mat[maxn];
// 两个矩阵相交里面的元素数量
int intersect(Matrix a, Matrix b) {
int xmin = min(a.dr.x, b.dr.x);
int xmax = max(a.dl.x, b.dl.x);
int ymin = max(a.ul.y, b.ul.y);
int ymax = min(a.dl.y, b.dl.y);
if (xmin < xmax || ymin > ymax) return 0;
// [xmax, xmin] * [ymin, ymax]
return sum[xmin][ymax] - sum[xmin][ymin-1] - sum[xmax-1][ymax] + sum[xmax-1][ymin-1];
}
int main() {
cin >> n >> m >> r;
fac[0] = 1;
for (int i = 1; i <= 2000; i++) fac[i] = fac[i-1] * i;
inv_fac[2000] = fac[2000].inv();
for (int i = 1999; i >= 1; i--) inv_fac[i] = inv_fac[i+1] * (i+1);
inv_fac[0] = 1;
for (int i = 1; i <= n; i++) {
cin >> x[i] >> y[i] >> b[i];
sum[x[i]][y[i]] = 1;
mat[i].ul.x = max(1, x[i] - r);
mat[i].ul.y = max(1, y[i] - r);
mat[i].ur.x = min(1000, x[i] + r);
mat[i].ur.y = max(1, y[i] - r);
mat[i].dl.x = max(1, x[i] - r);
mat[i].dl.y = min(1000, y[i] + r);
mat[i].dr.x = min(1000, x[i] + r);
mat[i].dr.y = min(1000, y[i] + r);
}
for (int i = 1; i <= 1e3; i++) {
for (int j = 1; j <= 1e3; j++) {
sum[i][j] += sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (max(abs(x[i] - x[j]), abs(y[i] - y[j])) <= r) {
adj[i].push_back(j);
}
}
}
for (int i = 1; i <= n; i++) {
Z r = b[i] * b[i] % mod; // 贡献
Z s = C(n, m) - C(n - adj[i].size(), m); // 方案
ans += r * s;
}
for (int i = 1; i <= n; i++) {
for (int j = i+1; j <= n; j++) {
// 计算方案数
Z s = C(n, m);
int x = adj[i].size() + adj[j].size() - intersect(mat[i], mat[j]);
s += C(n - x, m);
s -= C(n - adj[i].size(), m);
s -= C(n - adj[j].size(), m);
Z r = 2LL * b[i] * b[j] % mod;
ans += r * s;
}
}
cout << ans.val() << endl;
}
例2 CF1267K. Key Storage
题意
对于一个整数 $n$,我们定义它的一个multiset $f(n)$ 为:
初始序列为空,将 n % 2 放入multiset中,然后让 n /= 2,如果此时 $n > 0$,那么继续将 n % 3 放入multiset中,然后 n /= 3,以此类推。
持续执行这个操作直到 $n=0$。
给定一个正整数 $n$,求有多少个其他的正整数 $m$ 使得 $f(n)=f(m)$?
其中,$n \leq 10^{18}$。
题解
首先我们可以计算出 $n$ 对应的 $f(n)$。
那么对于 $f(n)$,我们从小到大来看这个 multiset,第一个位置是 % 2 的结果,所以值必须 $<2$,第二个位置是 % 3 的结果,所以必须 $<3$,以此类推。
• 最后一个位置不能为 $0$,因为除以最后一个数以后,$n$ 变成了 $0$,所以余数是不可能为 $0$ 的。
所以实际上,计算 $f(m)$ 的数量,也就是计算给每个位置填上 multiset 中的元素的方案数,这个方案数要满足以下条件:
- 第 $i$ 个位置的数 $<i+1$。
- 最后一个位置的数不能为 $0$。
先考虑第二种,我们不妨固定最后一位为 $0$,然后用无限制的方案数减去它即可。
现在只剩下第一个条件了,这其实是乘法原理,我们从小到大枚举位置,枚举到第 $i$ 位的时候,就将 $\leq i$ 的数加入选项中。
• 最后需要注意,我们计算的是 multiset 的数量,所以相同元素之间的顺序是无所谓的,所以还要把每个元素的数量的阶乘从答案里除掉。
代码
#include <bits/stdc++.h>
using namespace std;
ll cnt[30], fac[18];
int T;
int main() {
cin >> T;
fac[0] = 1;
for (int i = 1; i < 18; i++) fac[i] = fac[i-1] * i;
while (T--) {
ll n; cin >> n;
int m = 0;
for (int i = 2; ; i++) {
cnt[n % i]++;
n /= i;
m++;
if (!n) break;
}
ll sum = cnt[0], ans = 1;
for (int i = 1; i <= m; i++) {
// 第 i 个:<= i 的
sum += cnt[i];
ans = ans * (sum - i + 1);
}
ll tmp = 0;
if (cnt[0]) {
tmp = cnt[0]; // 最后一位固定为0,可以有 cnt[0] 种选法
sum = cnt[0] - 1; // 预设最后一个为 0
for (int i = 1; i < m; i++) {
sum += cnt[i];
tmp = tmp * (sum - i + 1);
}
}
ans -= tmp;
for (int i = 0; i < 18; i++) {
ans /= fac[cnt[i]];
}
ans--;
cout << ans << endl;
memset(cnt, 0, sizeof(cnt));
}
}
例3 Atcoder ABC152F. Tree and Constraints
题意
给定 $n$ 个节点的树,每个边可以被涂成黑色或者白色。
给定 $m$ 个constraint $(u_i,v_i)$,代表 $(u_i,v_i)$ 的路径上至少有一个黑色边?
求有多少钟涂色方案,使得所有constraint都被满足?
其中,$2 \leq n \leq 50, 1 \leq m \leq 20$。
题解
$m\leq 20$,一眼暴力。
这个至少有一条黑色边很不好处理,但它的补集是路径上所有都是白色边。这个就好办了。
所以令 $S_i$ 为:第 $i$ 个constraint没有被满足。
要求的是 $|S_1 \cup S_2 … \cup S_m|$,即至少有一个constraint没有被满足的方案数量。
根据容斥原理,就是 +1个不满足 - 2个不满足 + 3个不满足 …
所以我们直接bitmask枚举所有的情况,对于不满足的constraint,它们路径上的所有边只能涂白,剩下的所有边随便涂。然后根据奇偶性判断符号即可。
• 处理constraint的时候用树上差分。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 500+5;
const int maxm = 2e6+5;
int n, m;
vector<int> adj[maxn];
ll ans = 1;
pii p[maxn];
int count_bits(ll x) {
int res = 0;
while (x) {
if (x&1) res++;
x >>= 1;
}
return res;
}
int lca[maxn][maxn], par[maxn], dep[maxn], val[maxn];
void dfs(int u, int p) {
dep[u] = dep[p] + 1;
for (int v : adj[u]) {
if (v == p) continue;
par[v] = u;
dfs(v, u);
}
}
void init_lca(int u, int v) {
int tu = u, tv = v;
if (u == v) {
lca[u][v] = lca[v][u] = u;
return;
}
if (dep[u] < dep[v]) swap(u,v);
while (dep[u] > dep[v]) u = par[u];
assert(dep[u] == dep[v]);
while (u != v) {
u = par[u], v = par[v];
}
lca[tu][tv] = lca[tv][tu] = u;
}
ll cnt = 0;
void dfs2(int u, int p) {
for (int v : adj[u]) {
if (v == p) continue;
dfs2(v, u);
val[u] += val[v];
if (val[v] > 0) cnt++; // (u,v) must be white
}
}
ll p2[maxn];
int main() {
cin >> n;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 0);
p2[0] = 1;
for (int i = 1; i <= n; i++) p2[i] = p2[i-1] * 2;
ans = p2[n-1];
cin >> m;
for (int i = 1; i <= m; i++) cin >> p[i].first >> p[i].second;
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j++) {
init_lca(i,j);
}
}
for (int mask = 1; mask < (1<<m); mask++) {
int f = ((count_bits(mask) & 1) ? -1 : 1);
memset(val, 0, sizeof(val));
cnt = 0;
for (int j = 0; j < m; j++) {
if (mask&(1<<j)) { // j+1
int u = p[j+1].first, v = p[j+1].second;
val[u]++;
val[v]++;
val[lca[u][v]] -= 2;
}
}
dfs2(1, 0);
ans += f * p2[n-1-cnt];
}
cout << ans << endl;
}
