后缀数组
Contents
模版
代码(nlogn)
// sa[i]:所有的后缀排序后,第 $i$ 小的后缀的编号。(排第 $i$ 名的是 sa[i] 这个后缀)。
// rk[i]:后缀 $i$(指 s[i...n]) 的排名。(第 $i$ 个后缀的排名是 rk[i])。
// height[i]: LCP(sa[i-1], sa[i]),即第 $i-1$ 名的后缀和 第 $i$ 名的后缀的最长公共前缀长度
struct SA {
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], cnt[maxn], id[maxn], key1[maxn], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
char s[maxn];
int m = 127;
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(string& ss) {
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1];
for (int i = 1; i <= n; i++) rk[i] = s[i], cnt[rk[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;
int p = 0; // 当前值域
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
p = 0;
for (int i = n; i > n-w; i--) id[++p] = i;
for (int i = 1; i <= n; i++) {
if (sa[i] > w) id[++p] = sa[i] - w;
}
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++) key1[i] = rk[id[i]], cnt[key1[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[key1[i]]--] = id[i];
memcpy(oldrk+1, rk+1, n*sizeof(int));
p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
m = p;
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
}
void clear() {
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(cnt, 0, sizeof(cnt));
memset(id, 0, sizeof(id));
memset(key1, 0, sizeof(key1));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
m = 127; // 这个必须有!
}
} sa;
int n;
int main() {
cin >> n;
string s; cin >> s;
sa.init(s);
ll ans = (ll)(n) * (n+1) / 2;
for (int i = 1; i <= n; i++) ans -= sa.height[i];
cout << ans << "\n";
}
代码(nlog^2 n)
// sa[i]:所有的后缀排序后,第 $i$ 小的后缀的编号。(排第 $i$ 名的是 sa[i] 这个后缀)。
// rk[i]:后缀 $i$(指 s[i...n]) 的排名。(第 $i$ 个后缀的排名是 rk[i])。
// height[i]: LCP(sa[i-1], sa[i]),即第 $i-1$ 名的后缀和 第 $i$ 名的后缀的最长公共前缀长度
struct SA {
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
int s[maxn];
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(vector<int>& ss) { // 不再是普通的字符串,而是 vector<int> 了,注意长度就是 n,不要添加多余的元素!
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1], rk[i] = s[i], sa[i] = i;
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
sort(sa + 1, sa + n + 1, [&](int x, int y) {
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
});
memcpy(oldrk+1, rk+1, n*sizeof(int));
int p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
}
void clear() {
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
}
} sa;
int n;
int main() {
cin >> n;
vector<int> vec;
for (int i = 1; i <= n; i++) {
int x; cin >> x; vec.push_back(x);
}
sa.init(vec);
}
介绍
后缀数组可以对一个字符串的所有后缀进行排序,然后得到一些有用的信息。
在处理出后缀数组后,我们会得到以下数组:
sa[i]:所有的后缀排序后,第 $i$ 小的后缀的编号。(排第 $i$ 名的是sa[i]这个后缀)。rk[i]:后缀 $i$ 的排名。(第 $i$ 个后缀的排名是rk[i])。第 $i$ 个后缀指的是 $s[i…n]$。height[i]:LCP(sa[i-1], sa[i]),即第 $i-1$ 名的后缀和 第 $i$ 名的后缀的最长公共前缀长度。
• 对于第 $i$ 名的后缀和第 $j$ 名的后缀的 LCP 长度($i<j$),可以直接用 $\min\limits_{k=i+1}^j height[k]$ 求出。
算法
暴力的思路是求出所有后缀,然后排序,复杂度是 $O(n^2 \log n)$。
利用倍增可以在 $O(n \log n)$ 求出后缀数组。
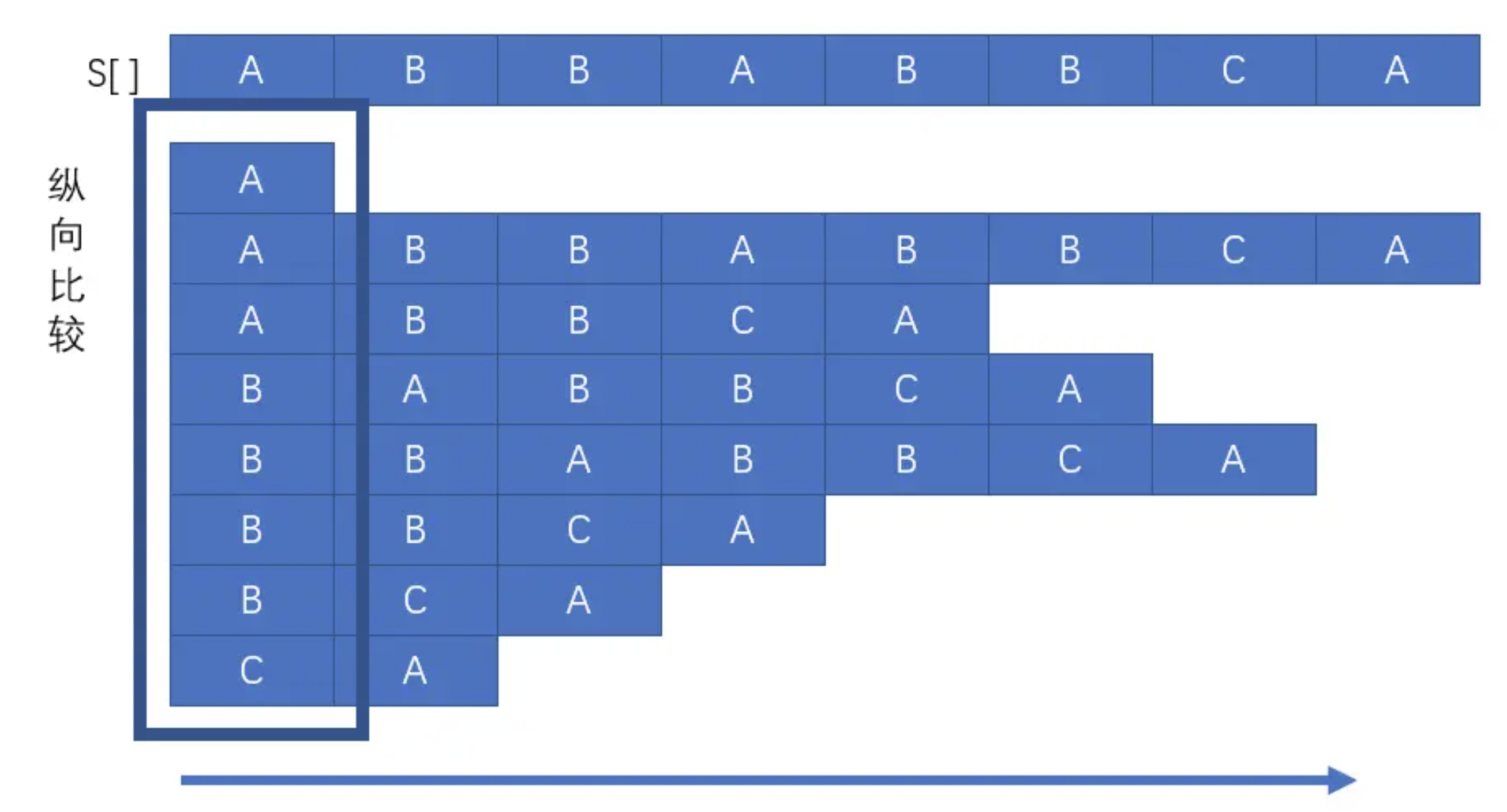
如上图,我们先比较每个后缀的第一个字符。

这样我们可以得到第一个字符的排序(注意这个例子和上面那个不同了)。
接下来比较第二个字符,这样和第一个字符的排序结合起来,可以得到一个双关键字的排序。
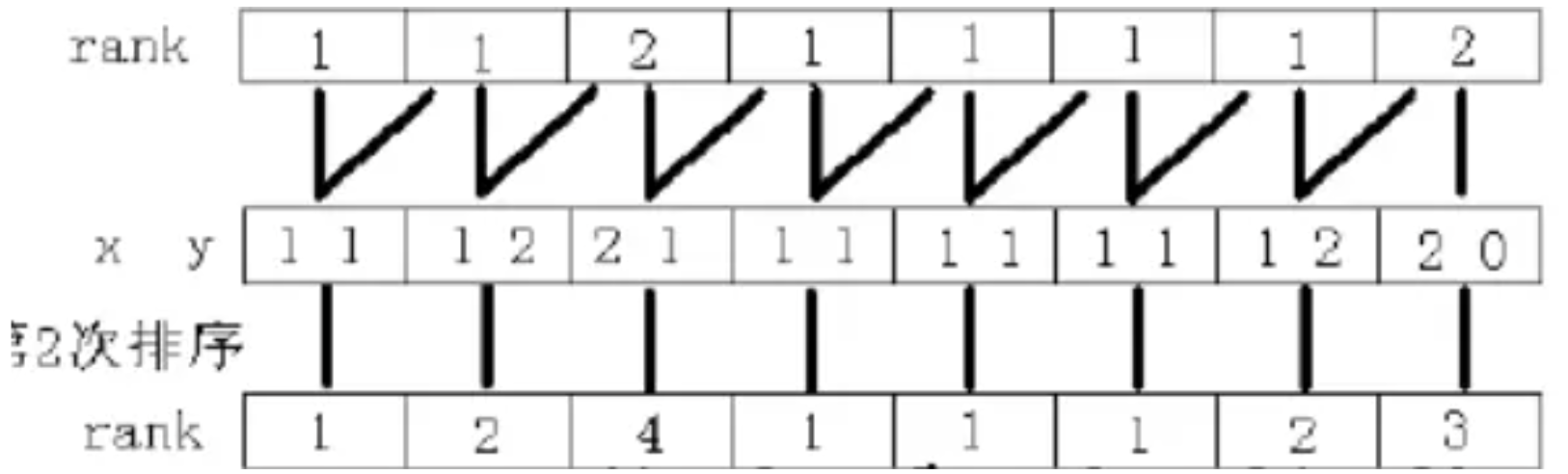
双关键字排序后,又可以得到一个排名,然后注意到此时每个排名都代表 $2$ 个字符长度的排名。
所以两个排名结合起来就对应了 $4$ 个字符长度的排名,于是就可以利用倍增继续双关键字排序,如下:
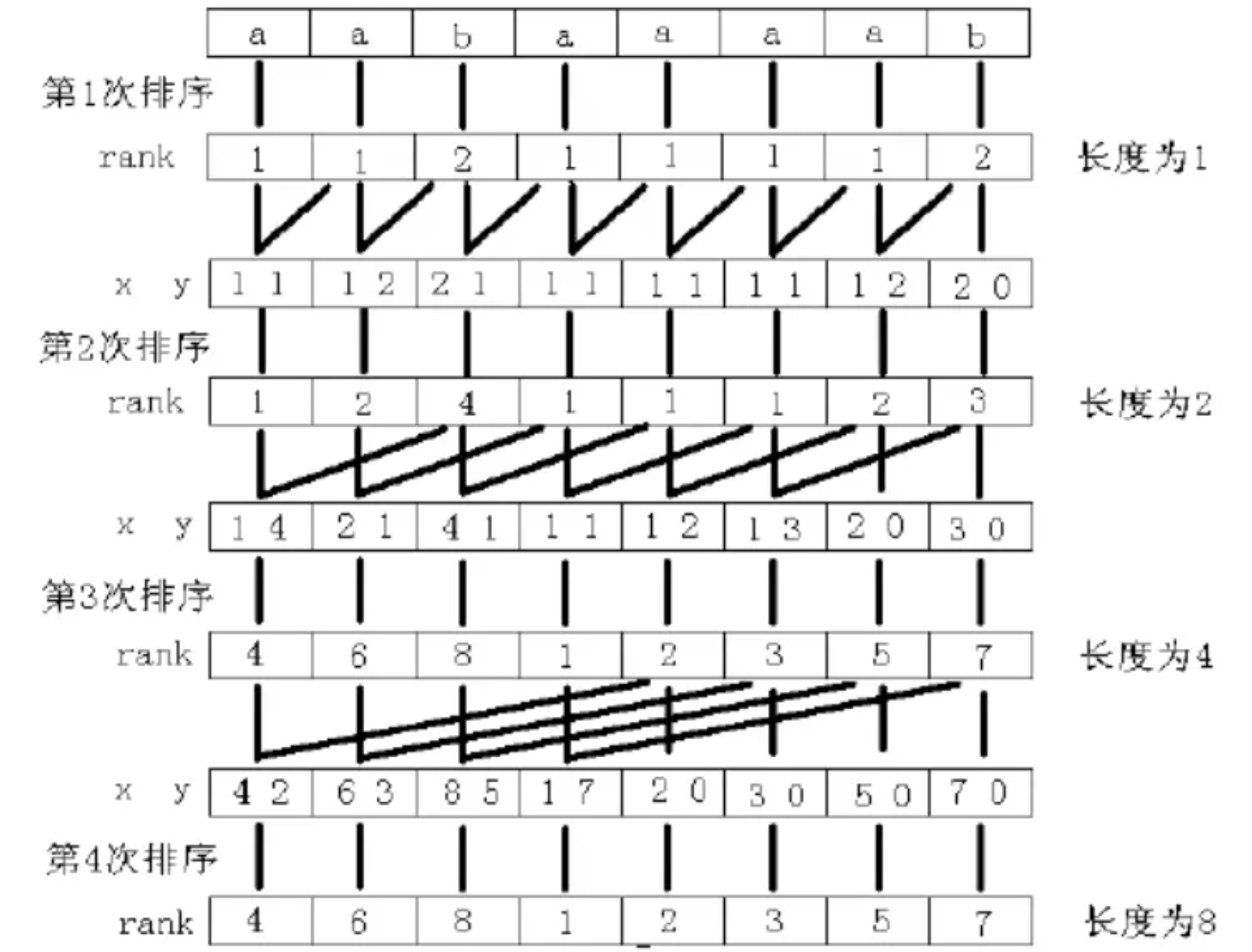
由于字符串值域被ASCII码限制在 $127$ 内,如果用 counting sort,复杂度为 $O(n\log n)$。
不过在一些情况下,可能需要用 int 来表示一个字符串,这个时候要么扩大值域范围(代码中的 m=127),要么使用 $O(n\log^2 n)$ 的方法。
应用
求不同子串数量
见 例1。
比较字符串中,两个子串的大小关系
如果需要比较 $A = S[a…b]$ 和 $B = S[c…d]$ 的大小关系,那么:
求出后缀 $S[a…]$ 与 $S[c…]$ 的 LCP长度,设其为 $L$。
若 $L \geq \min(|A|,|B|)$,那么 $A < B \iff |A| < |B|$。
若 $L < \min(|A|,|B|)$,那么 $A < B \iff rk[a] < rk[c]$。
查询一个/多个模式串 $T$ 在文本串 $S$ 中出现的所有位置
处理出 $S$ 的后缀数组,由于后缀是 sorted 的,所以可以在后缀数组上二分 $T$ 的 lower_bound 和 upper_bound 位置。
设 $L$ 为 lower_bound, $R$ 为 upper_bound,则后缀数组上 $[L,R]$ 内对应的所有位置就是 $T$ 出现的所有位置。
二分时,直接用 $|T|$ 的时间暴力比较即可。
• 如果 $S$ 的某个后缀长度不够 $|T|$,则仍然按正常的字符串比较方式判断大小。
复杂度:$O(|T|\log |S|)$。
也可以用于多模式串匹配,复杂度比哈希和 bitset 更加优秀,而且还支持在线。
代码
string s, t;
int main() {
cin >> s >> t;
int n = s.size(), m = t.size();
sa.init(s);
int low = 1, high = n, L = n+1, R = 0;
while (low <= high) {
int mid = (low + high) >> 1;
int st = sa.sa[mid];
int cp = 0;
for (int j = st; j <= min(n, st + m - 1); j++) {
if (s[j-1] < t[j-st]) {
cp = -1;
break;
}
if (s[j-1] > t[j-st]) {
cp = 1;
break;
}
}
if (st + m - 1 > n && !cp) { // 长度不够了,但仍然相等,说明 t 更大
cp = -1;
}
if (!cp) {
L = mid; // 区别
}
if (cp >= 0) { // 区别
high = mid - 1;
} else low = mid + 1;
}
low = 1, high = n;
while (low <= high) {
int mid = (low + high) >> 1;
int st = sa.sa[mid];
int cp = 0;
for (int j = st; j <= min(n, st + m - 1); j++) {
if (s[j-1] < t[j-st]) {
cp = -1;
break;
}
if (s[j-1] > t[j-st]) {
cp = 1;
break;
}
}
if (st + m - 1 > n && !cp) {
cp = -1;
}
if (!cp) {
R = mid; // 区别
}
if (cp > 0) { // 区别
high = mid - 1;
} else low = mid + 1;
}
vector<int> res;
for (int i = L; i <= R; i++) {
res.push_back(sa.sa[i]);
}
sort(res.begin(), res.end()); // 从小到大排序
for (int x : res) cout << x << "\n";
}
多个字符串的最长公共子串
用 不同的分隔符 将这些字符串连在一起,然后利用滑动窗口,保证窗口内每一个来源的后缀都存在时,用 ST 表求窗口的 height[] 最小值即可。
• 注意需要不同的分隔符,否则会有影响(至于分隔符是比所有字符大还是小都无所谓)。不过需要用 $O(n\log^2 n)$ 版本的算法,保证不受值域影响。
见 例7。
出现至少 $k$ 次的子串的最大长度
如果一个子串在母串中出现了至少 $k$ 次,设其长度为 $L$。这意味着至少有 $k$ 个后缀的LCP的长度 $\geq L$。
那么二分这个长度 $L$,然后在 height 数组里观察,是否有连续 $(k-1)$ 个数 $\geq L$ 即可。
见 例8。
$t$ 的每一个前缀在 $s$ 中出现的所有位置
给定一个字符串 $s$,每次询问给定另外一个字符串 $t$,我们需要知道 $t$ 的每一个前缀 $t[1…i]$ 在 $s$ 中的哪些位置出现了?
任何字符串如果出现在 $s$ 中了,那么它出现的位置一定是后缀数组上的一个连续的区间 $[L,R]$。
假设 $p[1…i]$ 对应的区间是 $[L,R]$,而 $p[1…i+1]$ 对应的区间是 $[L’,R’]$,那么一定有 $[L’,R’] \subseteq [L,R]$。
于是直接枚举前缀长度,从 $1$ 枚举到 $m$,枚举过程中缩小 $[L,R]$ 这个区间,缩小的方式就是比较当前前缀的最后一个字母与 $L,R$ 对应的后缀相应位置的字母的大小(因为我们已经保证了 $p[1…i]$ 对应的区间是 $[L,R]$,所以只需要比较当前后缀的最后一个字母)。
见例9。
例题
例1 洛谷P2408 不同子串个数
题意
给定一个长度为 $n$ 的字符串 $s$,求 $s$ 内不同的子串个数。
其中,$n \leq 10^5$。
题解
答案就是 全部子串数量 $- \sum\limits_{i=2}^n height[i]$。
考虑排序后排名第 $i$ 的后缀(长度为 $m$)贡献了哪些新的子串,有且仅有 $m - height[i]$。
因为跟排名 $i-1$ 的后缀比较,新贡献的肯定是这么多。
如果贡献的数量 $< m - height[i]$,说明这个后缀的前缀在之前的某一个位置出现过了,这说明 $LCP(j, i) > height[i]$,其中 $j < i-1$,这与 $LCP(j,i) = \min\limits_{k=j+1}^i height[k]$ 冲突了。
代码
同模版。
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
cin >> n;
string s; cin >> s;
sa.init(s);
ll ans = (ll)(n) * (n+1) / 2;
for (int i = 1; i <= n; i++) ans -= sa.height[i];
cout << ans << "\n";
}
例2 洛谷P2870 [USACO07DEC]Best Cow Line G
题意
给定一个长度为 $n$ 的字符串 $s$,每次可以从 $s$ 的首部和尾部字符中选一个出来,直到 $s$ 为空,求能够获得的字典序最小的字符串。
其中,$n \leq 5 \times 10^5$。
题解
当首尾字符不一样时,肯定选较小的那个。
当首尾字符一样时,我们就继续看第 $2$ 个和第 $n-1$ 个字符,如果还是一样就继续对比,直到第一个不一样的为止。
但这样是 $O(n^2)$ 的。
我们观察一下可以发现,首尾字符一样时,本质是比较 $s$ 的一个后缀,和 $s'$ (反过来的 $s$) 的一个后缀的大小。
那么比较两个字符串的后缀的大小,我们在后缀数组里可以 $O(1)$ 做到。
将两个字符串拼在一起的方法是 s + '@' + s',其中 @ 是一个比所有字符都小的字符,这样保证它在后缀数组中不会影响到 $s,s'$ 后缀的计算。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
string s, ans;
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) {
char c; cin >> c; s += c;
}
string t = s;
s += (char)('A' - 1);
reverse(t.begin(), t.end());
s += t;
sa.init(s);
int i = 1, j = n;
while (i <= j) {
if (s[i-1] < s[j-1]) ans += s[i-1], i++;
else if (s[i-1] > s[j-1]) ans += s[j-1], j--;
else {
// 比较 s[i] 开始的后缀和 t[2n+2-j] 开始的后缀的大小
if (sa.rk[i] < sa.rk[2*n+2-j]) ans += s[i-1], i++;
else ans += s[j-1], j--;
}
}
int cnt = 0;
for (int i = 0; i < n; i++) {
cout << ans[i];
if (++cnt == 80) cnt = 0, cout << "\n";
}
}
例3 最长公共子串 LCS
题意
给定两个字符串 $s,t$,长度分别为 $n,m$。求最长公共子串的长度。
其中,$n,m \leq 2.5 * 10^5$。
• 子串指的是 Substring,是连续的。
题解
首先利用经典套路,将 $s,t$ 中间用一个极小的字符连在一起。
然后要求最长公共子串,可以发现必然来自于两个后缀的 LCP,而这两个后缀是来自于不同字符串的。
而我们知道任意两个后缀的 LCP 可以用height数组计算出来,并且是取一个范围 min 的,很显然每个后缀只用考虑左边和右边第一个和它来源于不同字符串的后缀,求LCP即可。
然而可以更简单:因为是取范围min,所以直接考虑排名 $i-1$ 和 $i$ 的后缀,来源的字符串是否不同,如果不同的话就 ans = max(ans, height[i]) 即可。
代码
#include <bits/stdc++.h>
using namespace std;
int from[maxn]; // from[i] = 1: s, from[i] = 2: t
int main() {
int n, m;
string s, t; cin >> s >> t;
n = s.size(), m = t.size();
string S = s + (char)('a' - 1) + t;
sa.init(S);
for (int i = 1; i <= n; i++) {
from[sa.rk[i]] = 0;
}
for (int i = n+2; i <= n+m+1; i++) {
from[sa.rk[i]] = 1;
}
from[sa.rk[n+1]] = 2;
int ans = 0;
for (int i = 2; i <= n+m+1; i++) {
if ((from[i] ^ 1) == from[i-1]) ans = max(ans, sa.height[i]);
}
cout << ans << endl;
}
例4 NOI2015 品酒大会
题意
给定一个长度为 $n$ 的字符串 $S$,并且位置 $i$ 有权值 $a_i$。
现在定义位置 $p,q$ 是 “$r$ 相似的” 当且仅当:
$$S[p…p+r-1] = S[q…q+r-1]$$
现在对于每一个 $r=0,1,2,…,n-1$,都回答以下两个问题:
-
有多少个pair $(p,q)$,使得 $p,q$ 是 “$r$ 相似的”?其中 $p<q$。
-
输出所有 “$r$ 相似的” 的 pair $(p,q)$ 中,$a_p * a_q$ 的最大值。
其中,$n \leq 3 \times 10^5, |a_i| \leq 10^9$。
题解
如果 $(p,q)$ 是 “$r$ 相似的”,意味着 $p,q$ 位置的 LCP 长度 $\geq r$。
先考虑第一个问题,有多少个pair是 “$r$ 相似的”?
本质上是在问,在height数组上,有多少个 pair $(p,q)$ 的区间最小值是 $\geq r$ 的?
我们不妨将整个数组视为一个拥有 $n$ 个空格子的数组,询问 $r$ 时,我们将所有 $<r$ 的位置加上一个障碍物,那么剩下来的就是若干个空格子组成的一些联通块。
如果一个联通块大小为 $x$,那么它就贡献了 $1+2+…+x = \frac{x(x+1)}{2}$ 的数量。
然而,如果我们从小往上加障碍物,将一个大的联通块分成若干个小联通块,很明显不好计算,所以我们反过来做。
从 $r=n-1$ 开始到 $0$,逐渐消掉障碍物,相当于将一些小联通块合并在一起,可以用并查集实现。
接下来解决第二个问题,$a_p * a_q$ 的最大值。
在我们得到联通块之后,答案就是每一个联通块 $[L,R]$ 内,求 $p,q \in [L,R]$,$a_p * a_q$ 的最大值。
由于 $a_i$ 有正有负有 $0$,所以我们用线段树解决这个问题:
每个节点里记录这个区间内,正数的最大值和最小值,负数的最大值和最小值,再记录是否存在 $0$。
然后 $a_p * a_q$ 的最大值就来自于 left child 和 right child 的最大值,以及正数/负数的最大/小值的两两组合,如果有 $0$ 的话再与 $0$ 取个最大值即可。
所以在并查集合并过程中,每次合并两个区间,就更新 count 和 最大值即可。
代码
#include <bits/stdc++.h>
using namespace std;
ll cal(ll x) {
return x*(x+1)/2;
}
ll val[maxn];
struct Node {
ll ans; // -1e18
ll neg[2], pos[2]; // neg[0] < neg[1], pos[0] < pos[1], neg = {1e9, 1e9}, pos = {-1e9, -1e9}
bool haszero; // 0
};
struct SegmentTree {
Node tr[maxn<<2];
Node init() {
Node res;
res.ans = -1e18;
res.neg[0] = res.neg[1] = 1e9; // neg[0] > 0, 代表这个区间不存在负数
res.pos[0] = res.pos[1] = -1e9; // pos[0] < 0, 代表这个区间不存在正数
res.haszero = 0;
return res;
}
void init(int cur, int p) {
tr[cur] = init();
tr[cur].haszero = (!val[p]);
if (val[p] > 0) tr[cur].pos[0] = tr[cur].pos[1] = val[p];
if (val[p] < 0) tr[cur].neg[0] = tr[cur].neg[1] = val[p];
}
void push_up(int cur) {
int lc = cur<<1, rc = lc + 1;
tr[cur] = merge(tr[lc], tr[rc]);
}
Node merge(Node lc, Node rc) {
Node cur = init();
cur.ans = max(lc.ans, rc.ans);
if (lc.haszero || rc.haszero) cur.ans = max(cur.ans, 0LL), cur.haszero = 1;
for (int o1 = 0; o1 < 2; o1++) {
for (int o2 = 0; o2 < 2; o2++) {
if (lc.neg[o1] < 0 && rc.neg[o2] < 0) cur.ans = max(cur.ans, lc.neg[o1] * rc.neg[o2]);
if (lc.neg[o1] < 0 && rc.pos[o2] > 0) cur.ans = max(cur.ans, lc.neg[o1] * rc.pos[o2]);
if (lc.pos[o1] > 0 && rc.neg[o2] < 0) cur.ans = max(cur.ans, lc.pos[o1] * rc.neg[o2]);
if (lc.pos[o1] > 0 && rc.pos[o2] > 0) cur.ans = max(cur.ans, lc.pos[o1] * rc.pos[o2]);
}
}
if (lc.neg[0] < 0) cur.neg[0] = cur.neg[1] = lc.neg[0];
if (rc.neg[0] < 0) cur.neg[0] = cur.neg[1] = rc.neg[0];
if (lc.pos[0] > 0) cur.pos[0] = cur.pos[1] = lc.pos[0];
if (rc.pos[0] > 0) cur.pos[0] = cur.pos[1] = rc.pos[0];
if (lc.neg[0] < 0) cur.neg[0] = min(cur.neg[0], lc.neg[0]), cur.neg[1] = max(cur.neg[1], lc.neg[1]);
if (rc.neg[0] < 0) cur.neg[0] = min(cur.neg[0], rc.neg[0]), cur.neg[1] = max(cur.neg[1], rc.neg[1]);
if (lc.pos[0] > 0) cur.pos[0] = min(cur.pos[0], lc.pos[0]), cur.pos[1] = max(cur.pos[1], lc.pos[1]);
if (rc.pos[0] > 0) cur.pos[0] = min(cur.pos[0], rc.pos[0]), cur.pos[1] = max(cur.pos[1], rc.pos[1]);
return cur;
}
Node query(int cur, int l, int r, int L, int R) {
if (l >= L && r <= R) return tr[cur];
int mid = (l+r) >> 1;
Node res = init();
Node lres = init(), rres = init();
if (L <= mid) lres = query(cur<<1, l, mid, L, R);
if (R > mid) rres = query(cur<<1|1, mid+1, r, L, R);
if (L <= mid && R <= mid) return lres;
if (L > mid && R > mid) return rres;
assert(L <= mid && R > mid);
return merge(lres, rres);
}
void build(int cur, int l, int r) {
if (l == r) {
init(cur, l);
return;
}
int mid = (l+r) >> 1;
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
push_up(cur);
}
} tr;
int n;
ll cnt = 0, ans = -1e18;
struct UnionFind {
int par[maxn], sz[maxn], L[maxn], R[maxn];
int finds(int u) {
if (!par[u]) return 0;
if (par[u] == u) return u;
return par[u] = finds(par[u]);
}
bool unions(int u, int v) {
u = finds(u), v = finds(v);
if (u == v || !u || !v) return 0;
if (sz[u] < sz[v]) swap(u, v);
cnt -= (cal(sz[u]) + cal(sz[v]));
sz[u] += sz[v];
cnt += cal(sz[u]);
par[v] = u;
L[u] = min(L[u], L[v]);
R[u] = max(R[u], R[v]);
ans = max(ans, tr.query(1, 1, n, L[u]-1, R[u]).ans);
return 1;
}
void init(int u) {
par[u] = u;
sz[u] = 1;
L[u] = R[u] = u;
cnt++;
ans = max(ans, tr.query(1, 1, n, L[u]-1, R[u]).ans);
}
} uf;
ll a[maxn];
string s;
vector<int> pos[maxn];
int main() {
cin >> n >> s;
for (int i = 1; i <= n; i++) cin >> a[i];
sa.init(s);
for (int i = 2; i <= n; i++) {
pos[sa.height[i]].push_back(i);
}
for (int i = 1; i <= n; i++) {
int r = sa.sa[i];
val[i] = a[r];
}
tr.build(1, 1, n);
vector<pll> vec;
for (int i = n-1; i >= 0; i--) {
for (int p : pos[i]) {
uf.init(p);
}
for (int p : pos[i]) {
uf.unions(p, p-1);
uf.unions(p, p+1);
}
if (cnt > 0)
vec.push_back({cnt, ans});
else
vec.push_back({cnt, 0});
}
reverse(vec.begin(), vec.end());
for (auto [x, y] : vec) cout << x << " " << y << "\n";
}
例5 HAOI2016 找相同字符
题意
给定两个字符串 $s,t$,求出:在两个字符串中各取出一个子串,使得这两个子串相同的方案数。
其中,$|s|,|t| \leq 2 \times 10^5$。
题解
先将两个字符串粘在一起,然后对于每个pair $(p,q)$,求出 LCP 以后,可以知道这个 pair 对答案的贡献就是对应的 LCP 的长度。
所以问题转化为,求
$$\sum\limits_{i<j} LCP(i,j)$$
不过,我们还要保证 $p,q$ 分别来自于 $s$ 和 $t$ 才行。
于是我们可以先在 $s,t$ 上分别求出 $\sum\limits_{i<j} LCP(i,j)$,然后在 $S = s+t$ 上再求一次,减掉即可。
现在问题是怎么求
$$\sum\limits_{i<j} LCP(i,j)$$
不难发现上一题已经有答案了:
只要求出有多少个pair是 “$r$ 相似的” 即可,所以套用上题代码。
代码
#include <bits/stdc++.h>
using namespace std;
// sa[i]:所有的后缀排序后,第 $i$ 小的后缀的编号。(排第 $i$ 名的是 sa[i] 这个后缀)。
// rk[i]:后缀 $i$ 的排名。(第 $i$ 个后缀的排名是 rk[i])。
// height[i]: LCP(sa[i-1], sa[i]),即第 $i-1$ 名的后缀和 第 $i$ 名的后缀的最长公共前缀长度
struct SA {
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], cnt[maxn], id[maxn], key1[maxn], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
char s[maxn];
int m = 127;
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void clear() {
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(cnt, 0, sizeof(cnt));
memset(id, 0, sizeof(id));
memset(key1, 0, sizeof(key1));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
m = 127;
}
void init(string& ss) {
clear();
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1];
for (int i = 1; i <= n; i++) rk[i] = s[i], cnt[rk[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;
int p = 0; // 当前值域
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
p = 0;
for (int i = n; i > n-w; i--) id[++p] = i;
for (int i = 1; i <= n; i++) {
if (sa[i] > w) id[++p] = sa[i] - w;
}
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++) key1[i] = rk[id[i]], cnt[key1[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[key1[i]]--] = id[i];
memcpy(oldrk+1, rk+1, n*sizeof(int));
p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
m = p;
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
}
};
ll cal(ll x) {
return x*(x+1) / 2;
}
int n;
ll cnt = 0;
struct UnionFind {
int par[maxn], sz[maxn];
int finds(int u) {
if (!par[u]) return 0;
if (par[u] == u) return u;
return par[u] = finds(par[u]);
}
bool unions(int u, int v) {
u = finds(u), v = finds(v);
if (u == v || !u || !v) return 0;
if (sz[u] < sz[v]) swap(u, v);
cnt -= (cal(sz[u]) + cal(sz[v]));
sz[u] += sz[v];
cnt += cal(sz[u]);
par[v] = u;
return 1;
}
void init(int u) {
par[u] = u;
sz[u] = 1;
cnt++;
}
void clear() {
memset(par, 0, sizeof(par));
memset(sz, 0, sizeof(sz));
}
};
UnionFind uf;
SA sa;
vector<int> pos[maxn];
ll solve(string s) {
sa.init(s);
cnt = 0;
uf.clear();
int n = s.size();
for (int i = 0; i <= n; i++) pos[i].clear();
for (int i = 2; i <= n; i++) {
pos[sa.height[i]].push_back(i);
}
ll res = 0;
for (int i = n-1; i >= 1; i--) {
for (int p : pos[i]) {
uf.init(p);
}
for (int p : pos[i]) {
uf.unions(p, p-1);
uf.unions(p, p+1);
}
res += cnt;
}
return res;
}
int main() {
string s, t; cin >> s >> t;
ll ans = -solve(s) - solve(t);
s = s + (char)('a' - 1) + t;
ans += solve(s);
cout << ans << endl;
}
例6 NOI2016 优秀的拆分
题意
如果一个字符串可以被拆分为 $\text{AABB}$ 的形式,其中 $\text{A}$ 和 $\text{B}$ 是非空字符串,则我们称该字符串的这种拆分是优秀的。
一个字符串可能存在多种优秀的拆分。
现在给出一个长度为 $n$ 的字符串 $S$,求出它所有子串中,优秀拆分的方案数的和。
其中,$n \leq 30000$。
题解
对于每一个位置 $i$,如果求出两个数组 pre[i], suf[i]。
pre[i] 表示以 $i$ 作为结尾,AA 类型字符串的数量。
suf[i] 代表以 $i$ 作为开头,AA 类型字符串的数量。
那么答案就等于
$$\sum\limits_{i=1}^n \text{pre}_{i-1}*\text{suf}_i$$
例如 "aabaab" 这个字符串,对于位置 $1$ 来说,suf[1] = 2,因为位置 $1$ 作为开头,有 "aa" 和 "aabaab" 两个 “AA” 类型的字符串。
现在问题是怎么求出 pre[], suf[]?
我们枚举 “AA” 类型字符串中,“A” 的长度,设为 $k$。
然后我们在 $1, k+1, 2k+1, 3k+1, …$ 位置设立一个特殊点。
对于第 $j$ 个特殊点和第 $j-1$ 个特殊点(假设坐标分别为 $i, i-k$),让我们来看一下它们观测到了哪些 “AA” 类型字符串?
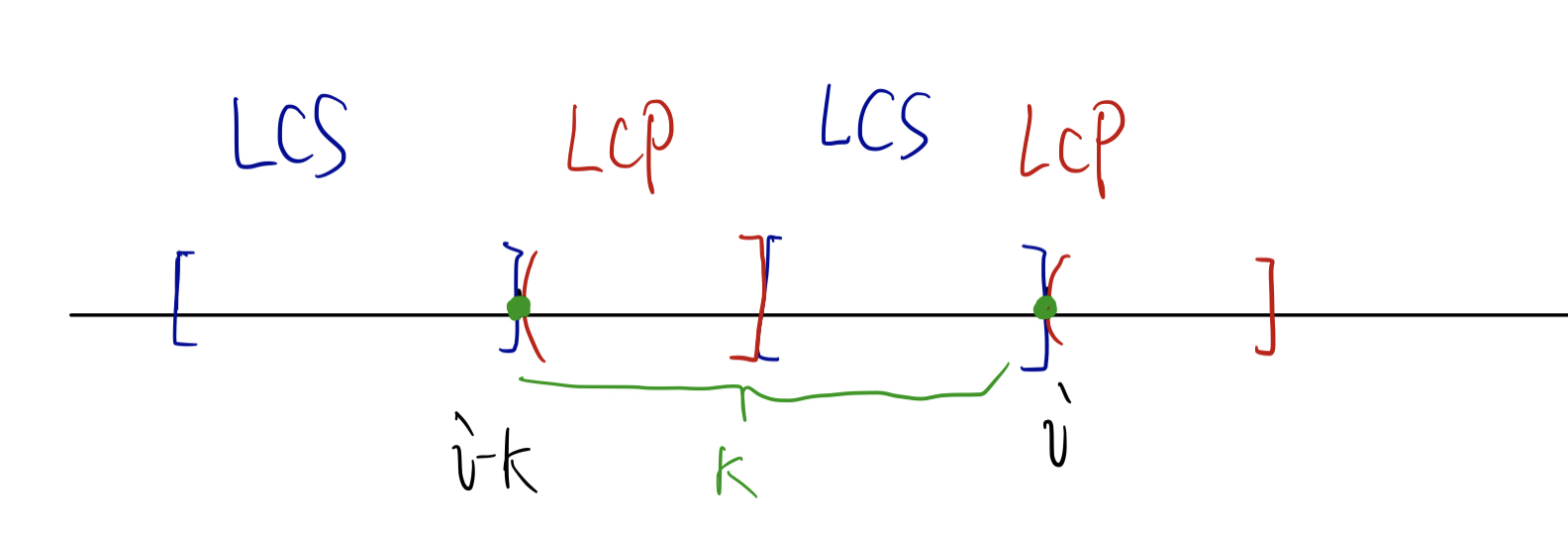
对于这两个特殊点,我们计算它们的后缀的 LCP 和前缀的 LCS(最长公共后缀)。
假设 $|LCP| + |LCS| - 1 \geq k$(-1是因为观测点本身只被考虑一次)(图上画的是刚好等于的情况),就说明它观测到了至少一个 “AA” 类型字符串。
例如图上,“AA” 类型字符串的 “A” 就是从第一个蓝色的 [ 开始,到第一个红色的 ] 结束。
如果 $|LCP| + |LCS| - 1 > k$ 的话,观测到的则是多个 “AA” 类型字符串,不难发现将是一整个区间都是 “A” 的开始点。
所以利用差分数组来记录 “A” 的开始位置。
不过也要注意,如果字符串 $S$ 是 aaaaa.... 这种类型的,那么 LCP 和 LCS 的长度可能会非常长,长到覆盖了其他特殊点。
所以我们规定,第 $i$ 个特殊点只考虑到 第 $i-1$ 个特殊点的这段区间,只考虑这段区间内计算出来的 “A” 的开始点。
suf[] 同理。
一顿暴力手搓式子以后就可以了,代码很简洁。
• 求 LCS 和 LCP 就用 ST表。
代码
#include <bits/stdc++.h>
using namespace std;
struct SparseTable {
int n;
vector<int> a;
int st[maxn][18], bin[maxn];
int ask_st(int l, int r) {
int len = r-l+1;
int k = bin[len];
return min(st[l][k], st[r-(1<<k)+1][k]);
}
void build_st() {
bin[1] = 0; bin[2] = 1;
for (int i = 3; i < maxn; i++) bin[i] = bin[i>>1] + 1;
for (int i = 1; i <= n; i++) st[i][0] = a[i];
for (int k = 1; k < 18; k++) {
for (int i = 1; i + (1<<k) - 1 <= n; i++)
st[i][k] = min(st[i][k-1], st[i+(1<<(k-1))][k-1]);
}
}
};
struct SA {
SparseTable st;
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], cnt[maxn], id[maxn], key1[maxn], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
char s[maxn];
int m = 127;
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(string& ss) {
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1];
for (int i = 1; i <= n; i++) rk[i] = s[i], cnt[rk[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;
int p = 0; // 当前值域
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
p = 0;
for (int i = n; i > n-w; i--) id[++p] = i;
for (int i = 1; i <= n; i++) {
if (sa[i] > w) id[++p] = sa[i] - w;
}
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++) key1[i] = rk[id[i]], cnt[key1[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[key1[i]]--] = id[i];
memcpy(oldrk+1, rk+1, n*sizeof(int));
p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
m = p;
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
st.n = n;
st.a.resize(n+5);
for (int i = 1; i <= n; i++) {
st.a[i] = height[i];
}
st.build_st();
}
void clear() {
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(cnt, 0, sizeof(cnt));
memset(id, 0, sizeof(id));
memset(key1, 0, sizeof(key1));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
m = 127;
}
};
int n, pre[maxn], suf[maxn];
void solve() {
memset(pre, 0, sizeof(pre));
memset(suf, 0, sizeof(suf));
SA sa, sa2; sa.clear(); sa2.clear();
string s; cin >> s;
n = s.size();
string t = s; reverse(t.begin(), t.end());
sa.init(s), sa2.init(t);
for (int k = 1; k < n; k++) {
for (int i = k+1; i <= n; i += k) {
int j = i-k;
int ri = sa.rk[i], rj = sa.rk[j];
if (ri > rj) swap(ri, rj);
int R = sa.st.ask_st(ri+1, rj);
ri = sa2.rk[n-i+1], rj = sa2.rk[n-j+1];
if (ri > rj) swap(ri, rj);
int L = sa2.st.ask_st(ri+1, rj);
if (L + R - 1 < k) continue;
suf[max({j-L+1, 1, j-k+1})]++, suf[min(j,j+R-k)+1]--; // [j-L+1, j+R-k]
pre[max(i,i-L+k)]++, pre[min({i+k-1, n, i+R-1})+1]--; // [i-L+k, i+R-1]
}
}
for (int i = 1; i <= n; i++) pre[i] += pre[i-1], suf[i] += suf[i-1];
ll ans = 0;
for (int i = 1; i <= n; i++) {
ans += (ll)pre[i-1] * suf[i];
}
cout << ans << endl;
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
例7 UVA11107 Life Forms
题意
给定 $n$ 个字符串,求最长子串,使得这个子串在超过 $\frac{n}{2}$ 个字符串中出现了。
其中,$n \leq 100$,所有字符串长度 $\leq 1000$。
若有多个长度相同的子串满足条件,将它们全部输出。若无答案输出 ?。
题解
将所有字符串连在一起(注意需要使用 不同的分隔符!!)
然后用滑动窗口,保证窗口内的后缀的来源超过 $\frac{n}{2}$ 个字符串即可,然后在滑动的过程中,窗口满足这个条件的话就用ST表求出最长子串。
• 由于有100个分隔符,只能用 int 而不能用 string 了,并且使用 $O(n\log^2 n)$ 的算法。
• 注意特判一下 $n=1$ 的情况。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5000;
// sa[i]:所有的后缀排序后,第 $i$ 小的后缀的编号。(排第 $i$ 名的是 sa[i] 这个后缀)。
// rk[i]:后缀 $i$ 的排名。(第 $i$ 个后缀的排名是 rk[i])。
// height[i]: LCP(sa[i-1], sa[i]),即第 $i-1$ 名的后缀和 第 $i$ 名的后缀的最长公共前缀长度
struct SparseTable {
int n;
vector<int> a;
int st[maxn][18], bin[maxn];
int ask_st(int l, int r) {
int len = r-l+1;
int k = bin[len];
return min(st[l][k], st[r-(1<<k)+1][k]);
}
void build_st() {
bin[1] = 0; bin[2] = 1;
for (int i = 3; i < maxn; i++) bin[i] = bin[i>>1] + 1;
for (int i = 1; i <= n; i++) st[i][0] = a[i];
for (int k = 1; k < 18; k++) {
for (int i = 1; i + (1<<k) - 1 <= n; i++)
st[i][k] = min(st[i][k-1], st[i+(1<<(k-1))][k-1]);
}
}
};
struct SA {
SparseTable st;
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
int s[maxn];
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(vector<int>& ss) { // 不再是普通的字符串,而是 vector<int> 了,注意长度就是 n,不要添加多余的元素!
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1], rk[i] = s[i], sa[i] = i;
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
sort(sa + 1, sa + n + 1, [&](int x, int y) {
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
});
memcpy(oldrk+1, rk+1, n*sizeof(int));
int p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
st.n = n;
st.a.resize(n+5);
for (int i = 1; i <= n; i++) {
st.a[i] = height[i];
}
st.build_st();
}
void clear() {
st.n = 0;
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
memset(st.st, 0, sizeof(st.st));
st.a.clear();
}
} sa;
int n, from[maxn], cnt[maxn];
string s[maxn];
void solve() {
memset(from, 0, sizeof(from));
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++) s[i] = "";
sa.clear();
int N = 0;
vector<int> S;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int c : s[i]) S.push_back(c);
if (i < n) {
S.push_back((int)'z' + i);
}
}
if (n == 1) {
cout << s[1] << "\n";
return;
}
N = S.size();
sa.init(S);
int len = 0;
for (int i = 1; i <= n; i++) {
for (int j = len + i; j <= len + i + s[i].size() - 1; j++) {
from[sa.rk[j]] = i;
}
len += s[i].size();
}
int L = 1, R = 0, sum = 0, ans = 0;
while (R <= N) {
while (R+1 <= N && sum < n/2 + 1) {
if (from[R+1]) {
int f = from[R+1];
cnt[f]++;
if (cnt[f] == 1) sum++;
}
R++;
}
while (L+1 <= R && sum >= n/2 + 1) {
if (from[L]) {
ans = max(ans, sa.st.ask_st(L+1, R));
int f = from[L];
cnt[f]--;
if (cnt[f] == 0) sum--;
}
L++;
}
if (R == N && sum < n/2 + 1) break;
}
L = 1, R = 0, sum = 0;
memset(cnt, 0, sizeof(cnt));
set<string> res;
while (R <= N) {
while (R+1 <= N && sum < n/2 + 1) {
if (from[R+1]) {
int f = from[R+1];
cnt[f]++;
if (cnt[f] == 1) sum++;
}
R++;
}
while (L+1 <= R && sum >= n/2 + 1) {
if (from[L]) {
if (sum >= n/2 + 1 && ans && sa.st.ask_st(L+1, R) == ans) {
res.insert(string(S.begin() + sa.sa[R] - 1, S.begin() + sa.sa[R] + ans - 1));
}
int f = from[L];
cnt[f]--;
if (cnt[f] == 0) sum--;
}
L++;
}
if (R == N && sum < n/2 + 1) break;
}
if (res.size()) {
for (string x : res) cout << x << "\n";
} else cout << "?\n";
}
int main() {
int T = 0;
while (cin >> n && n) {
if (T > 0) cout << "\n";
T++;
solve();
}
}
例8 洛谷P2852 [USACO06DEC] Milk Patterns G
题意
给定一个长度为 $n$ 的数组,和一个正整数 $k$。
求出现了至少 $k$ 次的子数组的最大长度。
其中,$n \leq 20000, k \in [2,n], a_i \in [0,10^7]$。
代码
#include <bits/stdc++.h>
using namespace std;
struct SA {
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
int s[maxn];
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(vector<int>& ss) { // 不再是普通的字符串,而是 vector<int> 了,注意长度就是 n,不要添加多余的元素!
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1], rk[i] = s[i], sa[i] = i;
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
sort(sa + 1, sa + n + 1, [&](int x, int y) {
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
});
memcpy(oldrk+1, rk+1, n*sizeof(int));
int p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
}
void clear() {
st.n = 0;
memset(sa, 0, sizeof(sa));
memset(rk, 0, sizeof(rk));
memset(oldrk, 0, sizeof(oldrk));
memset(height, 0, sizeof(height));
memset(s, 0, sizeof(s));
memset(st.st, 0, sizeof(st.st));
st.a.clear();
}
} sa;
int n, k;
bool check(int x) {
int cnt = 0;
for (int i = 2; i <= n; i++) {
if (sa.height[i] >= x) cnt++;
else {
if (cnt >= k-1) return 1;
cnt = 0;
}
}
if (cnt >= k-1) return 1;
return 0;
}
int main() {
cin >> n >> k;
vector<int> a;
for (int i = 1; i <= n; i++) {
int x; cin >> x;
a.push_back(x);
}
sa.init(a);
int low = 0, high = n, ans = 0;
while (low <= high) {
int mid = (low + high) >> 1;
if (check(mid)) {
low = mid+1;
ans = mid;
} else high = mid-1;
}
cout << ans << endl;
}
例9 CF149E Martian Strings
题意
给定一个长度为 $n$ 的字符串 $s$,然后给定 $q$ 个询问,每次询问给一个字符串 $p$,询问是否存在 $1 \leq L_1 \leq R_1 < L_2 \leq R_2 \leq n$ 使得:
$$s[L_1…R_1] + s[L_2…R_2] = p$$
其中,$n \leq 10^5, q \leq 100, |p_i| \leq 1000$。
题解
我们思考以下问题:
对于 $p$ 的每一个前缀 $p[1…i]$,我们是否能找出这个前缀在 $s$ 中出现的所有位置?并找到出现位置中,最靠前的那一个。
如果能解决上述问题,我们可以:
-
先求出 $p$ 的每一个前缀在 $s$ 中最靠前的位置。
-
将 $s$ 和 $p$ 都反过来得到 $s’, p'$,然后求出 $p'$ 的每一个前缀在 $s'$ 中最靠前的位置。
-
枚举 $p$ 的前缀长度 $j$(对应可得到 $p'$ 的前缀长度等于 $m-j$),然后判断一下两个出现位置是否有重叠即可,如果没有说明有解。
于是我们思考怎么解决上述问题。
首先,由于后缀数组中所有后缀是 sorted 的,所以任何字符串如果出现在 $s$ 中了,那么它出现的位置一定是后缀数组上的一个连续的区间 $[L,R]$,这个特性我们在 利用二分来查找子串 中也看到了。
假设我们知道 $p[1…i]$ 对应的区间是 $[L,R]$,而 $p[1…i+1]$ 对应的区间是 $[L’,R’]$,那么一定有 $[L’,R’] \subseteq [L,R]$,因为条件更苛刻了。
由于这个特性,令 $L=1, R=n$。我们直接枚举前缀长度,从 $1$ 枚举到 $m$,枚举过程中缩小 $[L,R]$ 这个区间,缩小的方式就是比较当前前缀的最后一个字母与 $L,R$ 对应的后缀相应位置的字母的大小(因为我们已经保证了 $p[1…i]$ 对应的区间是 $[L,R]$,所以只需要比较当前后缀的最后一个字母)。
这样对于 $p$ 的每一个前缀,就都可以求出它出现在 $s$ 中的所有位置了。
要找到最靠前的那一个,我们用 ST 表维护 sa.sa[] 这个数组的区间最小值即可。
复杂度:$O(n\log n + \sum m)$
• 对于 $|p| = 1$ 的情况直接返回 false 即可。
KMP做法:
说到后缀就想到SA,说到前缀那必然是想到 KMP 了。
KMP虽然无法求出 $p$ 的每一个前缀在 $s$ 中出现的所有位置,但是可以求出每个前缀出现的最靠前位置,在 kmp 的子串匹配中就可以很轻松的做到了。
后缀数组代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5000;
struct SparseTable {
int n;
vector<int> a;
int st[maxn][18], bin[maxn];
int ask_st(int l, int r) {
int len = r-l+1;
int k = bin[len];
return min(st[l][k], st[r-(1<<k)+1][k]);
}
void build_st() {
bin[1] = 0; bin[2] = 1;
for (int i = 3; i < maxn; i++) bin[i] = bin[i>>1] + 1;
for (int i = 1; i <= n; i++) st[i][0] = a[i];
for (int k = 1; k < 18; k++) {
for (int i = 1; i + (1<<k) - 1 <= n; i++)
st[i][k] = min(st[i][k-1], st[i+(1<<(k-1))][k-1]);
}
}
};
struct SA {
SparseTable st;
int n, sa[maxn], rk[maxn<<1], oldrk[maxn<<1], cnt[maxn], id[maxn], key1[maxn], height[maxn]; // 注意 rk[maxn<<1] oldrk[maxn<<1]
char s[maxn];
int m = 127;
bool cmp(int i, int j, int w) {
return oldrk[i] == oldrk[j] && oldrk[i+w] == oldrk[j+w];
}
void init(string& ss) {
n = ss.size();
for (int i = 1; i <= n; i++) s[i] = ss[i-1];
for (int i = 1; i <= n; i++) rk[i] = s[i], cnt[rk[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;
int p = 0; // 当前值域
for (int w = 1; w <= n; w <<= 1) { // 注意中间没有break的条件
p = 0;
for (int i = n; i > n-w; i--) id[++p] = i;
for (int i = 1; i <= n; i++) {
if (sa[i] > w) id[++p] = sa[i] - w;
}
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++) key1[i] = rk[id[i]], cnt[key1[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i-1];
for (int i = n; i >= 1; i--) sa[cnt[key1[i]]--] = id[i];
memcpy(oldrk+1, rk+1, n*sizeof(int));
p = 0;
for (int i = 1; i <= n; i++) {
rk[sa[i]] = cmp(sa[i], sa[i-1], w) ? p : (++p);
}
if (p == n) {
for (int i = 1; i <= n; i++) sa[rk[i]] = i;
break;
}
m = p;
}
// 求 height
int k = 0;
for (int i = 1; i <= n; i++) {
if (rk[i] == 0) continue;
if (k > 0) k--;
while (s[i+k] == s[sa[rk[i]-1]+k]) k++;
height[rk[i]] = k;
}
st.n = n;
st.a.resize(n+5);
for (int i = 1; i <= n; i++) {
st.a[i] = sa[i];
}
st.build_st();
}
} sa, sa2;
int n;
// ans[i]: t[1..i] 出现的最小位置(根据 sa 来决定是正着还是反着)
vector<int> getans(SA& sa, string t) {
int L = 1, R = n;
int m = t.size();
vector<int> ans(m+1, n+1);
ans[0] = 0;
for (int j = 1; j <= m; j++) {
// 比较 t[j-1]
while (L <= R) {
int st = sa.sa[L];
if (st + j - 1 > n || sa.s[st+j-1] < t[j-1]) { // 长度不够了 或者 t 更大
L++;
continue;
}
st = sa.sa[R];
if (st + j - 1 > n || sa.s[st+j-1] > t[j-1]) { // 长度不够了 或者 s 更大
R--;
continue;
}
break;
}
if (L > R) break;
ans[j] = sa.st.ask_st(L, R);
}
return ans;
}
bool solve(string t) {
if (t.size() == 1) return 0;
string t2 = t; reverse(t2.begin(), t2.end());
vector<int> ans1 = getans(sa, t);
vector<int> ans2 = getans(sa2, t2);
int m = t.size();
for (int j = 0; j <= m; j++) {
int ed1 = ans1[j] + j - 1;
int ed2 = (n-ans2[m-j]+1 - (m-j) + 1);
if (ed1 < ed2) {
return 1;
}
}
return 0;
}
string s, s2;
int main() {
cin >> s; sa.init(s);
n = s.size();
s2 = s; reverse(s2.begin(), s2.end()); sa2.init(s2);
int m; cin >> m;
int ans = 0;
while (m--) {
string t; cin >> t;
ans += solve(t);
}
cout << ans << endl;
}
KMP代码
#include <bits/stdc++.h>
using namespace std;
int n;
string s, s2;
// ans[i]: t[1..i] 出现的最小位置(根据 sa 来决定是正着还是反着)
vector<int> getans(string& s, string t) {
int m = t.size();
vector<int> ans(m+1, n+1);
ans[0] = 0;
vector<int> kmp(m+1, 0);
int j = 0;
for (int i = 2; i <= m; i++) {
while (j > 0 && t[i-1] != t[j]) j = kmp[j];
if (t[i-1] == t[j]) j++;
kmp[i] = j;
}
j = 0;
for (int i = 1; i <= n; i++) {
while (j > 0 && s[i-1] != t[j]) j = kmp[j];
if (s[i-1] == t[j]) j++;
ans[j] = min(ans[j], i-j+1);
if (j == m) {
j = kmp[j];
}
}
return ans;
}
bool solve(string t) {
if (t.size() == 1) return 0;
string t2 = t; reverse(t2.begin(), t2.end());
vector<int> ans1 = getans(s, t);
vector<int> ans2 = getans(s2, t2);
int m = t.size();
for (int j = 0; j <= m; j++) {
int ed1 = ans1[j] + j - 1;
int ed2 = (n-ans2[m-j]+1 - (m-j) + 1);
if (ed1 < ed2) {
return 1;
}
}
return 0;
}
int main() {
cin >> s;
n = s.size();
s2 = s; reverse(s2.begin(), s2.end());
int m; cin >> m;
int ans = 0;
while (m--) {
string t; cin >> t;
ans += solve(t);
}
cout << ans << endl;
}
