DFS/BFS树
Contents
介绍
在一个 无向图 中,DFS树是一个生成树(包含 $n-1$ 条边)。DFS树是在DFS过程中,如果从 dfs(u) 走到 dfs(v),那么 $(u,v)$ 这条边将会加入DFS树。
BFS树同理。
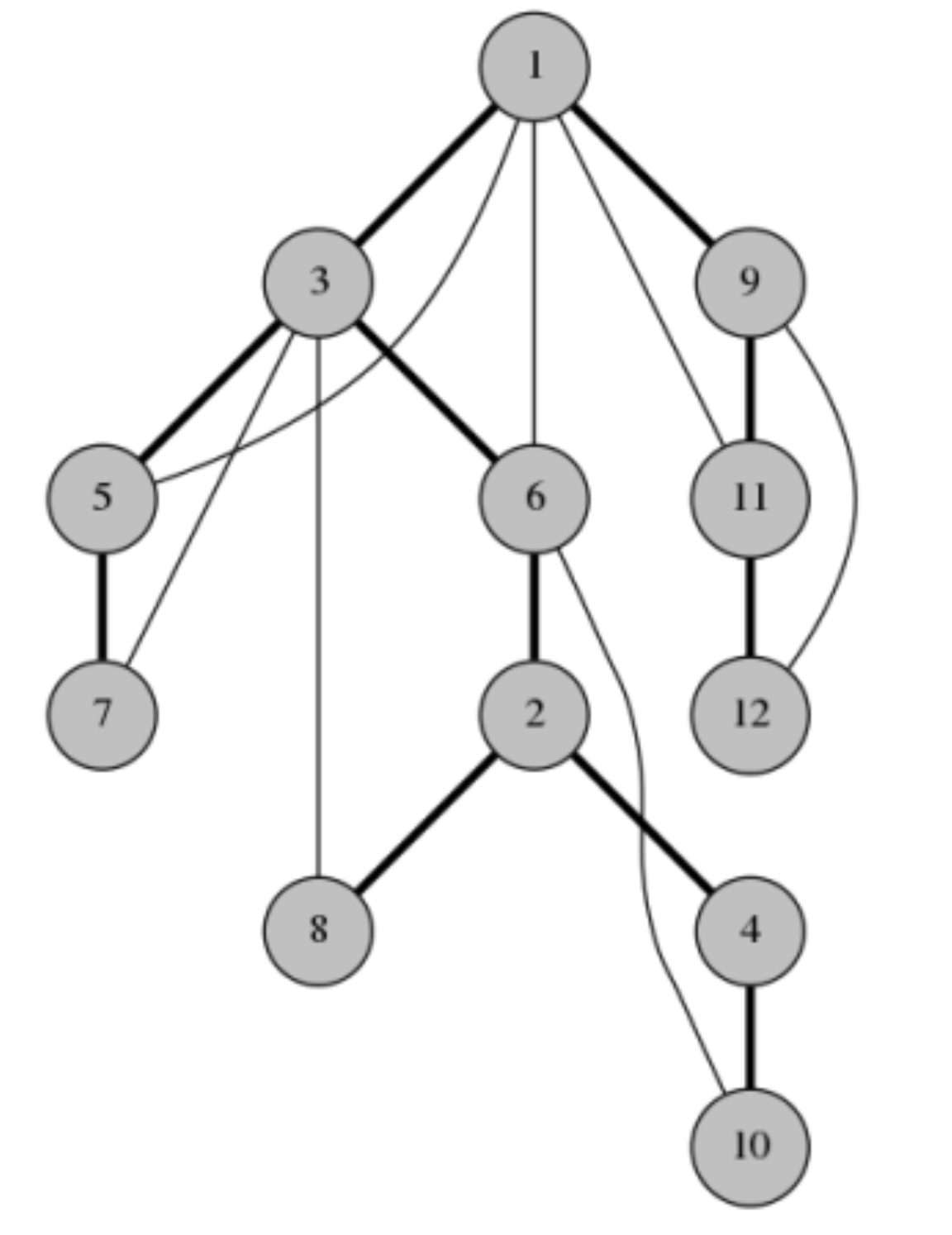
上图是一个 DFS 树的形状。
性质
DFS树
- 在 DFS 树中,所有的 非树边 $(u,v)$ 都一定是 back edge,即 $u$ 是 $v$ 的祖先(或者反过来),不可能出现 cross edge。
- 只有 DFS 的树边可能是桥,DFS的非树边不可能是桥。
- 如果一条树边 $(u,v)$ 是桥,那么 $v$ 的子树内不存在非树边指向 $u$ 的任意祖先。
- 对于任意的非树边 $(u,v)$,LCA一定是 $u$ (假设 $d_u < d_v$)。
证明:
- 如果一条非树边是 cross edge,那么 DFS 的过程中应该会沿着这条边访问,这条边应该是树边。
- 因为 DFS树 本身是一棵生成树,所以去掉所有非树边都仍然联通。
- 这其实就是 tarjan 的原理。
- 根据性质1易证。
BFS树
- 在 BFS 树中,所有的 非树边 $(u,v)$ 一定 不是 back edge,即 $u$ 一定与 $v$ 没有祖孙关系,并且 $u,v$ 的深度相差至多 $1$。
证明:
- 如果一条非树边 $(u,v)$ 中,$u,v$ 的深度相差 $\geq 2$,那么 BFS 的过程一定会通过 $u$ 走到 $v$,所以 $(u,v)$ 是树边。
例题
例1 ABC251F. Two Spanning Trees
题意
给定一个无向图,求两个生成树 $T_1,T_2$ 分别满足:
$T_1$:若以 $1$ 为根,对于所有的非树边 $(u,v)$,$u,v$ 互为子孙。
$T_2$:若以 $1$ 为根,对于所有的非树边 $(u,v)$,$u,v$ 互不为子孙。
其中,$n,m \leq 2 \times 10^5$,保证图是联通的。
题解
$T_1$ 就是 DFS 树,而 $T_2$ 就是 BFS 树。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
int n, m;
vector<int> adj[maxn];
bool vis[maxn];
vector<pii> dft, bft;
void dfs(int u) {
vis[u] = 1;
for (int v : adj[u]) {
if (vis[v]) continue;
dft.push_back({u,v});
dfs(v);
}
}
void bfs() {
queue<int> q;
q.push(1);
memset(vis, 0, sizeof(vis));
vis[1] = 1;
while (q.size()) {
int u = q.front(); q.pop();
for (int v : adj[u]) {
if (vis[v]) continue;
vis[v] = 1;
q.push(v);
bft.push_back({u,v});
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1);
bfs();
for (auto [u, v] : dft) cout << u << " " << v << "\n";
for (auto [u, v] : bft) cout << u << " " << v << "\n";
}
例2 CF118E. Bertown roads
题意
给定一个无向图,求是否存在一种方案让它变成有向图,并且任意两点之间仍然可以到达?如果有,输出这个方案。
其中,$n \leq 10^5, m \leq 3 \times 10^5$,原图是一个联通图。
题解
首先,如果原图存在桥,那么无解。
因为如果 $u,v$ 是一个桥,那么如果让它变成有向的 $u \rightarrow v$,那么 $v$ 就无法到达 $u$ 了。
判桥用 tarjan 即可。
没有桥说明有解,接下来考虑怎么变成有向图。
跑一个 DFS 树,然后结论是:
所有树边都从 parent 连向 child,所有非树边都从 child 连向 ancestor。
证明:首先可知根节点可以到达所有的点,只要证明所有的点均可以到达根节点即可。
考虑到这个图没有桥,意味着对于任意的树边 $u \rightarrow v$,$v$ 的子树内一定存在一个点,指向了 $u$ 的某个祖先。所以我们可以从 $u$ 出发,来到 $v$ 的子树中的某一个点,然后通过这条非树边来到 $u$ 的某个祖先。
由于没有桥,这个过程可以一直重复,也就是从任意点出发,都可以一直往它的祖先走,直到走到根。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
int n, m, dfn[maxn], low[maxn], id = 0;
vector<int> adj[maxn];
bool bridge = 0;
set<pii> se;
void tarjan(int u, int p) {
dfn[u] = low[u] = ++id;
for (int to : adj[u]) {
if (to == p) continue; // 注意不能用parent
if (dfn[to]) low[u] = min(low[u], dfn[to]);
else {
tarjan(to, u);
se.insert({u, to});
low[u] = min(low[u], low[to]);
if (low[to] > dfn[u]) { // 注意这里的条件
bridge = 1;
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
tarjan(1, 0);
if (bridge) {
cout << 0 << "\n";
return 0;
}
for (int u = 1; u <= n; u++) {
for (int v : adj[u]) {
if (dfn[u] < dfn[v]) {
if (se.count({u,v})) cout << u << " " << v << "\n";
else cout << v << " " << u << "\n";
}
}
}
}
例3 Universal Cup 16 H. Classical Maximization Problem
题意
给定 $2n$ 个二维平面上的互不相同的点。
求出最大数量的 pair,使得每一个pair都是两个点 $i,j$ 使得 $x_i = x_j$ 或者 $y_i = y_j$。
每个点只能存在于至多一个 pair 中。
输出最大pair的数量,以及pair的方案。
其中,$n \leq 10^5, x_i,y_i \in [-10^9, 10^9]$。
题解
将所有的 $x$ 坐标,$y$ 坐标作为一个点,每个点 $(x_i,y_i)$ 就是 $x_i \rightarrow y_i$ 的一条边。
这样可以多个联通分量,每个联通分量都是一个二分图。很明显联通分量之间是分开的。
然后问题转变成,找出最多的pair使得每两条边之间都有一个共同的点。先给一个结论:
对于大小为 $n$ 的联通分量,一定可以找到一种方案使得有 $\frac{n}{2}$ 个pair。
证明:
我们在这个图上跑一个 DFS 树,对于每棵子树 $v$,如果里面有偶数条边,那么它们一定可以在 $v$ 的子树内匹配完成。如果这个子树有奇数条边,那么它可以匹配到只剩下一条边,这条边就是连向 parent 的边。
如何证明?用归纳法:
考虑当前的节点 $u$,这个节点会有很多个儿子的子树,如果子树 $v$ 里面多了一条边,那么就是 $(u,v)$ 这条树边。
并且节点 $u$ 自己也会连一些非树边出来,由于这是 DFS 树,这个树边一定是连到 $u$ 的子树内的某个节点。
也就是说,这些多余的边全部都有 $u$ 这个共同点,那么它们之间就可以俩俩匹配了,所以 $u$ 也满足了偶数条边就可以全部匹配,奇数条边就只贡献一条边的特点。
这样递归的解决问题即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
const int maxm = 6e5+55;
int n;
struct Node {
int x, y, idx;
} a[maxn];
struct Edge {
int to, idx;
};
vector<Edge> adj[maxn<<1];
bool vis[maxn<<1];
vector<pii> ans;
int dep[maxn<<1];
// dfs 返回 >0 代表里面剩了一个边,这个边与 v 直接相连,编号就是返回值
int dfs(int u, int p) {
dep[u] = dep[p] + 1;
vis[u] = 1;
vector<int> vec;
for (auto [v, idx] : adj[u]) {
if (v == p) continue;
if (vis[v] && dep[v] < dep[u]) continue; // 如果这是一个backward edge
int r = 1;
if (!vis[v]) {
r = dfs(v, u);
if (r) {
ans.push_back({r, idx});
} else {
vec.push_back(idx);
}
} else vec.push_back(idx);
}
// vec 里面所有都是与 u 直接相连的
while (vec.size() >= 2) {
int i = vec.back(); vec.pop_back();
int j = vec.back(); vec.pop_back();
assert(i > 0); assert(j > 0);
ans.push_back({i,j});
}
if (vec.size()) return vec[0];
return 0;
}
void solve() {
int N = 0;
cin >> n; n*=2;
map<int, int> xs, ys;
for (int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y;
if (!xs.count(a[i].x)) xs[a[i].x] = ++N;
if (!ys.count(a[i].y)) ys[a[i].y] = ++N;
a[i].idx = i;
int u = xs[a[i].x], v = ys[a[i].y];
adj[u].push_back({v, i});
adj[v].push_back({u, i});
}
for (int i = 1; i <= N; i++) {
if (!vis[i]) dfs(i, 0);
}
vector<bool> used(n+5, 0);
cout << ans.size() << "\n";
for (auto [u,v] : ans) {
cout << u << " " << v << "\n";
used[u] = used[v] = 1;
}
vector<int> tmp;
for (int i = 1; i <= n; i++) {
if (!used[i]) tmp.push_back(i);
}
for (int i = 0; i < tmp.size(); i+=2) cout << tmp[i] << " " << tmp[i+1] << "\n";
ans.clear();
for (int i = 1; i <= N; i++) adj[i].clear();
fill(vis, vis+N+2, 0);
fill(dep, dep+N+2, 0);
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
例4 CF19E. Fairy
题意
给定一张无向图,现在需要恰好删掉一条边,问有多少种方案,使得恰好删除一条边后,得到的图是二分图。
输出所有的方案。
其中,$n,m \leq 10^4$。
题解
注意到一个图是二分图 $\iff$ 可以被二分染色 $\iff$ 没有奇环。
我们先跑一个 DFS 树出来,由于一棵树一定可以被二分染色,我们不妨先只考虑所有的树边,然后进行一个二分染色。
然后分别讨论树边和非树边。
首先,由于我们是根据树的结构来染色的,所以树边肯定不会有问题。但是非树边有可能会两端颜色相同,我们把两端颜色相同的非树边叫做 坏边,否则叫做 好边。
- 非树边:
在染色后,一个非树边可以成为答案,当且仅当 只有一条非树边是坏边。显然,如果有至少 $2$ 个坏边,那么怎么remove都不可能得到一个二分图的。
- 树边:
一个树边 $e$ 可以成为答案,当且仅当 所有的坏边 $(u,v)$ 在树上的路径均穿过 $e$,并且 没有好边 在树上的路径穿过 $e$。
所有的坏边必须穿过 $e$ 这一点好理解,由于坏边一定是构成了奇环,所以要断掉这个奇环,肯定得断掉环上的某一条边,如果存在一个坏边所在的奇环没有经过 $e$,那么断掉 $e$ 以后仍然存在奇环。
为什么还要保证没有好边在树上的路径穿过 $e$ 呢?
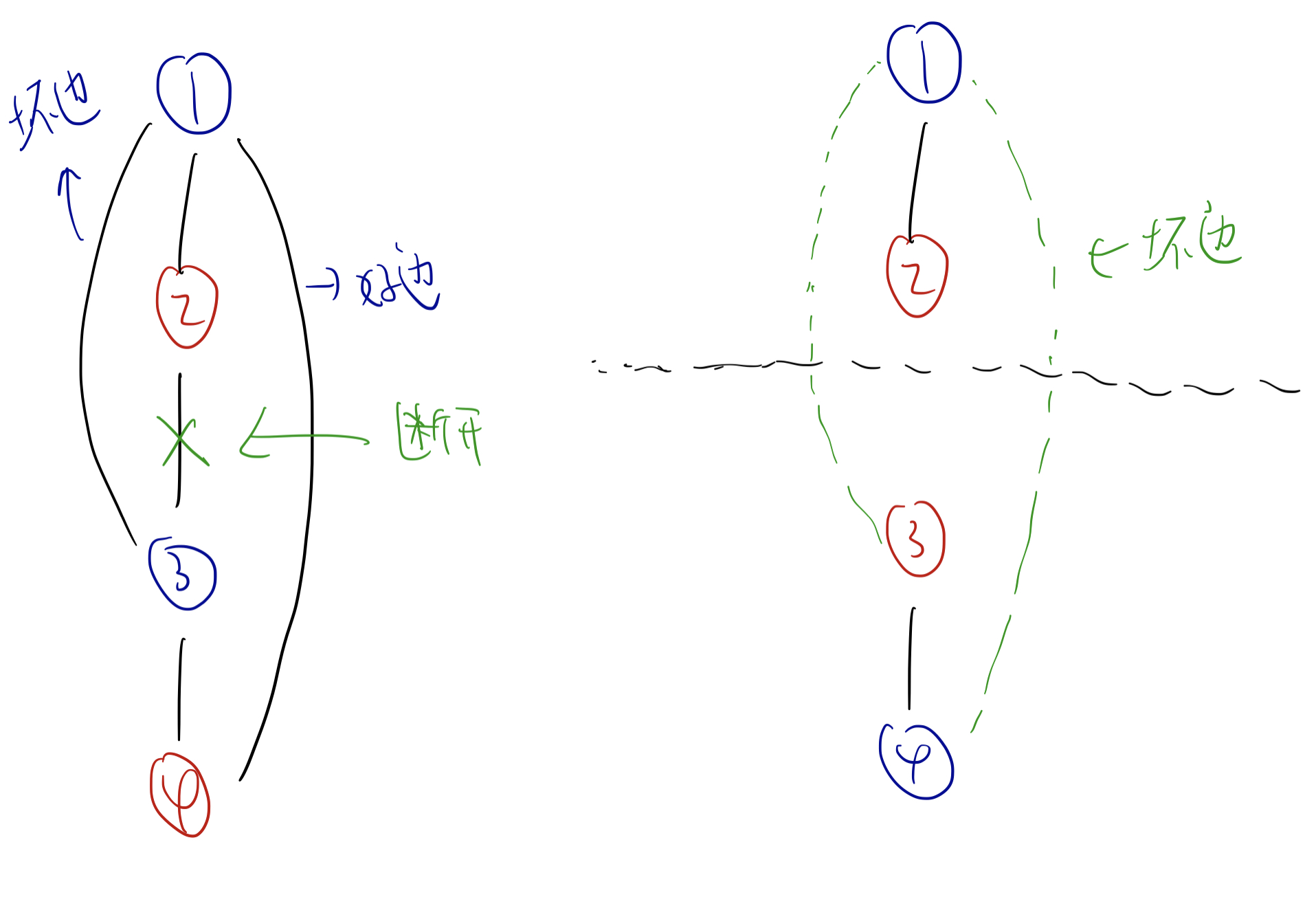
考虑这个例子,我们断开一条树边以后,如果我们暂时忽略掉非树边,那么我们可以得到两个联通块。由于坏边没有被删掉,所以坏边两端颜色还是相同。那么我们希望调整其中一个联通块的颜色,使得坏边两端的颜色不同。
而一个联通块内部为了保证染色的正确性,只能将整个联通块的颜色反转。此时如果有一个原先的好边,连接了这两个联通块,那么反转后它反而会变成坏边。
所以我们要保证没有好边在树上的路径穿过 $e$。
于是我们对于每个树边,都统计有多少条好边的路径,多少条坏边的路径穿过了它即可。
这是一个路径加,然后询问的问题。用树上差分即可实现,由于 DFS树 的特殊性质,一条非树边 $(u,v)$ 的 LCA 一定是 $u$,所以我们在 $O(1)$ 的时间就可以完成树上差分了。
• 最后注意一下原图并非联通图。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
const int maxm = 6e5+55;
int n, m, color[maxn];
struct Edge {
int u, v, idx;
};
vector<Edge> adj[maxn];
bool vis[maxn], istree[maxn]; // istree[i]: 第i条边是树边
bool bad[maxn]; // bad[i]: 第i条边不是树边,并且是坏边 (u,v颜色相同)
int badcnt = 0; // 有多少个联通块不是二分的
int badcomp = 0; // 这个联通块里有几个边是坏的
vector<int> tmp;
int good_dp[maxn], bad_dp[maxn], dep[maxn];
void dfs(int u, int p) {
dep[u] = dep[p] + 1;
vis[u] = 1;
for (auto [_, v, idx] : adj[u]) {
if (v == p) continue;
if (vis[v] && dep[u] > dep[v]) continue; // 必须是 ancestor -> child
if (!vis[v]) {
istree[idx] = 1;
color[v] = color[u] ^ 1;
dfs(v, u);
} else {
istree[idx] = 0;
// 坏边
if (color[u] == color[v]) {
badcomp++;
bad[idx] = 1;
tmp.push_back(idx);
bad_dp[v]++, bad_dp[u]--;
} else {
good_dp[v]++, good_dp[u]--;
}
}
}
}
vector<int> ans;
void dfs2(int u, int p) {
int pidx = -1;
for (auto [_, v, idx] : adj[u]) {
if (!istree[idx]) continue;
// 树边
if (v == p) {
pidx = idx;
LOG(pidx);
continue;
}
dfs2(v, u);
good_dp[u] += good_dp[v];
bad_dp[u] += bad_dp[v];
}
if (good_dp[u] == 0 && bad_dp[u] == badcomp && badcomp > 0) ans.push_back(pidx);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v; cin >> u >> v;
adj[u].push_back({u, v, i});
adj[v].push_back({v, u, i});
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
tmp.clear();
badcomp = 0;
dfs(i, 0);
badcnt += (badcomp > 0);
if (badcomp == 1) ans.push_back(tmp[0]);
dfs2(i, 0);
}
}
if (badcnt == 0) {
cout << m << "\n";
for (int i = 1; i <= m; i++) cout << i << " ";
return 0;
}
if (badcnt >= 2) {
cout << 0 << "\n";
return 0;
}
sort(ans.begin(), ans.end());
cout << ans.size() << "\n";
for (int i : ans) cout << i << " ";
cout << "\n";
}
