NAC2023 Training Camp Day2

A. Fair Bandwidth Sharing

题意

给定 $n$ 个区间 $[l_i, r_i]$，并且给定 $n$ 个权值 $d_i$，和一个常数 $t$。

定义 $y_i = t \frac{d_i}{\sum\limits_{j=1}^n d_j}$。

求一组 $x_i$，使得满足以下所有条件：

$\forall i \in [1,n], x_i \in [a_i, b_i]$。
$\sum\limits_{i=1}^n x_i = t$。
$\sum\limits_{i=1}^n \frac{(x_i-y_i)^2}{y_i}$ 最小。

其中，$n \leq 10^5, t \in [1,10^6], 0 \leq l_i \leq r_i \leq 10^6, r_i > 0, d_i \in [1,10^6]$。

题解

假设对于所有的 $i$，$d_i=1$，那么我们可以二分一个值 $z$，然后对于 $z$ 穿过的区间，就让 $x_i$ 取那个值，剩下的没有穿过的就让 $x_i$ 取边界，然后判断这个 $z$ 的值导致的 $\sum x_i$ 是 $>t$ 还是 $<t$。

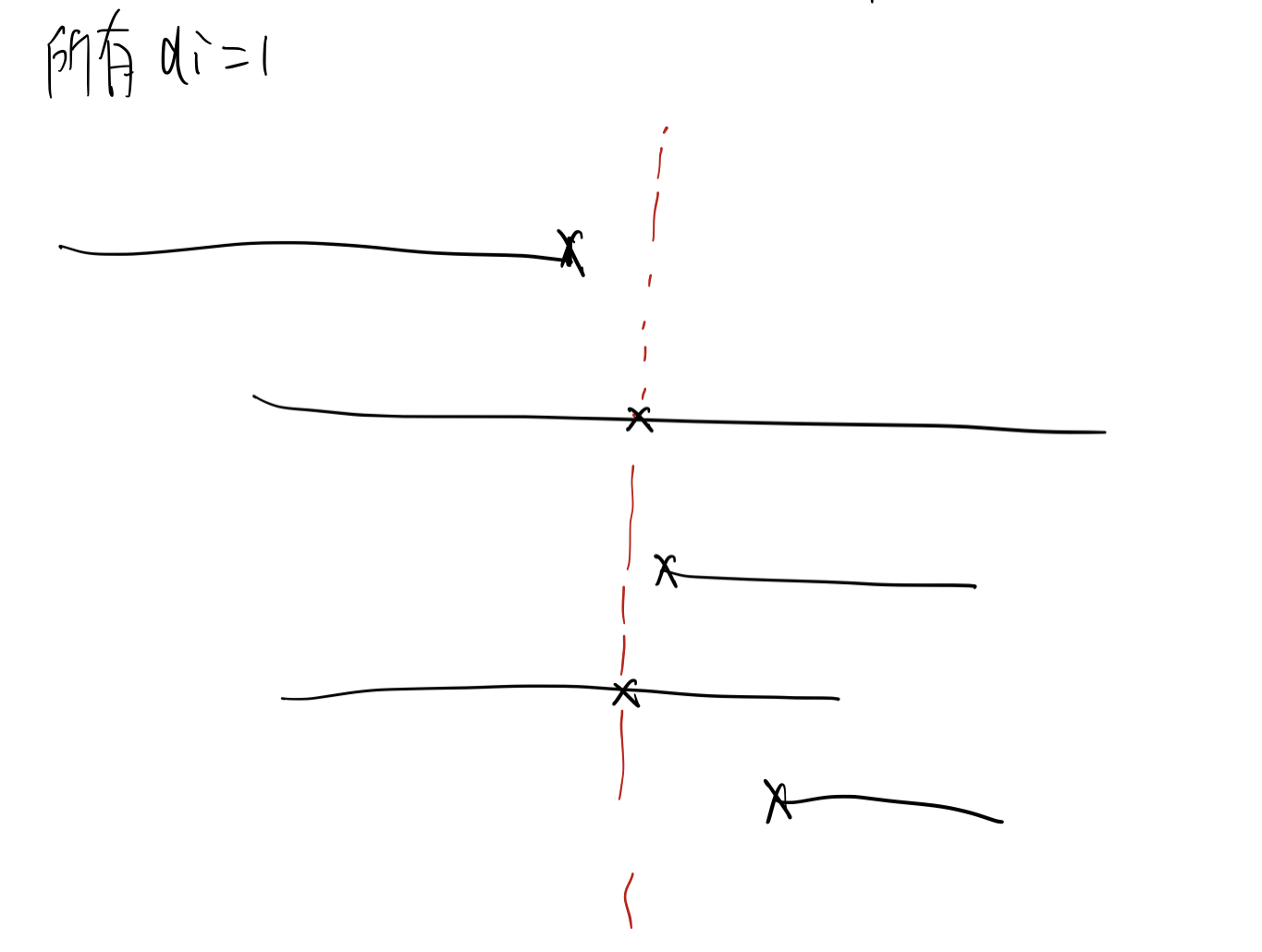
现在考虑 $d_i$ 不一定为 $1$ 的情况。首先我们处理一下使得 $\sum d_i = 1$。

那么对于式子 $\frac{(x_i-y_i)^2}{y_i}$ 中的变量 $x_i$ 求导可以得到 $\frac{2}{t}(\frac{x_i}{d_i} - t)$。由于 $t$ 是常数我们可以忽略不计。注意到这个导数是随着 $x_i$ 增大而增大的，而如果多个 $x_i$ 的导数相同，那么它们应该是根据 $d_i$ 的值等比例的。

于是衍生出了基于上述方法的新方法：

同样二分 $z$，但是 $x_i = z * d_i$，边界的话仍然取边界值，然后判断 $\sum x_i$ 是 $>t$ 还是 $<t$。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+55;

int n;
long double t;
int l[maxn], r[maxn];
double d[maxn], x[maxn];

// 取 
bool check(long double z) {
    long double res = 0.0;
    for (int i = 1; i <= n; i++) {
        x[i] = z * d[i];
        x[i] = max(x[i], (double)l[i]);
        x[i] = min(x[i], (double)r[i]);
        res += x[i];
    }
    return res >= t;
}


int main() {
    fastio;
    cin >> n >> t;
    long double sumd = 0.0;
    for (int i = 1; i <= n; i++) cin >> l[i] >> r[i] >> d[i], sumd += d[i];
    for (int i = 1; i <= n; i++) d[i] /= sumd;

    long double low = 0.0, high = 1e12;
    int T = 100;
    while (high - low > 1e-6 && T--) {
        long double mid = (low + high) * 0.5;
        if (check(mid)) {
            high = mid;
        } else low = mid;
    }
    for (int i = 1; i <= n; i++) {
        cout << setprecision(10) << x[i] << "\n";
    }
}

F. Factor-Free Tree

题意

给定一个长度为 $n$ 的数组 $a_1, a_2, …, a_n$。

是否存在一个二叉树，使得这个二叉树的 in-order 遍历的sequence等于这个数组，且保证对于每一个节点 $i$，它与它所有的祖先节点都互质。

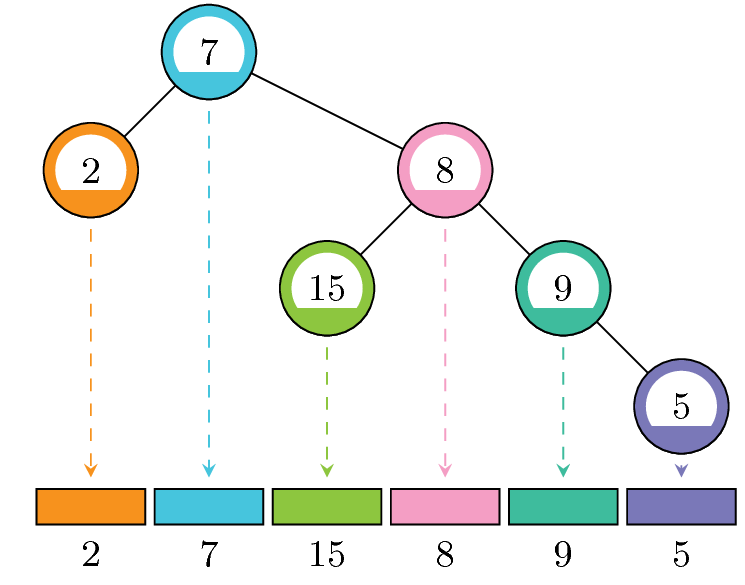
样例如上图。

如果有，输出方案。

其中，$n \leq 10^6, a_i \in [1, 10^7]$。

题解

很明显递归解决。对于 solve(l, r) 来说，确定一个根节点以后，保证这个根节点 $i \in [l,r]$ 并且 $i$ 与所有的 $[l,r]$ 内的数都互质即可。

但可能有很多这样的可行根节点。

一个重要猜想：随便选一个满足条件的根节点即可。

证明：假设我们找出了所有可行的根节点，那一个最佳方案是将这些根节点都split掉。这和我们按照顺序来split其实并无区别。所以随便选一个可行根节点即可。

那么只要知道，给定一个index的范围 $[L,R]$，从里面随便找出一个和其他都互质的数字即可。

这个好办，每个数字质因数分解一下，然后对于每一个质因数找到它们所在的位置，这样可以处理出两个数组 nxt[i] 表示 $a_i$ 右侧距离它最近的 $j$ 使得 $a_j$ 与 $a_i$ 不互质。同理可以得到 pre[i] 就是左侧最近的。

然后只要满足 nxt[i] > R && pre[i] < L 即可。

最后一个问题：复杂度是多少？

对于一个长度为 $n$ 的区间，我们最多需要 $O(n)$ 的时间找到这样的根 $i$，而最坏情况下可能会 split 成 $1, n-1$ 两个大小，所以看起来 $T(n) = T(1) + T(n-1) + O(n) = O(n^2)$？

一个很重要的优化：

我们在找这样的根 $i$ 时，不要从 $L$ 遍历到 $R$，而是从两边开始遍历，也就是 $L,R,L+1,R-1,L+2,R-2…$。

这样复杂度来到 $O(n\log n)$。

为什么呢？

因为这样可以最快的找到满足条件的根 $i$。假设 $\min(i-L+1, R-i+1) = k$，也就是根距离两个端点的最近距离，那么有

$$T(n) = T(k) + T(n-k-1) + 2k$$

那么最坏情况下是 $k=\frac{n}{2}$，也就是

$$T(n) = 2T(\frac{n}{2}) + n = O(n\log n)$$

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+55;
const int maxm = 1e7+5;
int n, a[maxn];
bool isPrime[maxm];
int small[maxm];
vector<int> primes;
void preprocess() {   // 线性筛优化
    memset(isPrime, 1, sizeof(isPrime));
    small[1] = 1;
    for (int i = 2; i <= maxm-5; i++) {
        if (isPrime[i]) primes.push_back(i), small[i] = i;
        for (int j = 0; j < primes.size() && i * primes[j] <= maxm-5; j++) {
            int cur = i * primes[j];
            isPrime[cur] = 0;
            small[cur] = primes[j];
            if (i % primes[j] == 0) break;
        }
    }
}
vector<int> pos[maxm];
int nxt[maxn], pre[maxn];


int par[maxn];

// if ok: return index of root
// if not ok: return 0
// if empty: return -1
int solve(int l, int r) {
    if (l > r) return -1;
    if (l == r) return l;

    // l, r, l+1, r-1, l+2, r-2
    int i = l, j = r;
    while (i <= j) {
        if (pre[i] < l && nxt[i] > r) {
            int lres = solve(l, i-1), rres = solve(i+1, r);
            if (lres == 0 || rres == 0) return 0;
            if (lres > 0) par[lres] = i;
            if (rres > 0) par[rres] = i;
            return i;
        }

        swap(i, j);
        if (pre[i] < l && nxt[i] > r) {
            int lres = solve(l, i-1), rres = solve(i+1, r);
            if (lres == 0 || rres == 0) return 0;
            if (lres > 0) par[lres] = i;
            if (rres > 0) par[rres] = i;
            return i;
        }
        swap(i, j);

        i++, j--;
    }
    return 0;
}

int main() {
    fastio;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    preprocess();
    fill(nxt, nxt+maxn, n+1);
    fill(pre, pre+maxn, 0);

    for (int i = 1; i <= n; i++) {
        int x = a[i];
        while (x > 1) {
            int sp = small[x];
            while (x % sp == 0) x /= sp;
            pos[sp].push_back(i);
        }
    }
    for (int sp = 2; sp <= maxm-5; sp++) {
        for (int i = 0; i < pos[sp].size(); i++) {
            int curp = pos[sp][i];
            if (i > 0) {
                pre[curp] = max(pre[curp], pos[sp][i-1]);
            }
            if (i < pos[sp].size() - 1) {
                nxt[curp] = min(nxt[curp], pos[sp][i+1]);
            }
        }
    }
    if (!solve(1, n)) {
        cout << "impossible\n";
    } else {
        for (int i = 1; i <= n; i++) cout << par[i] << " ";
        cout << "\n";
    }
}

Contents

A. Fair Bandwidth Sharing

F. Factor-Free Tree