笛卡尔树
Contents
定义
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 $(k,v)$ 构成。
性质
- $k$ 满足 BST 的性质
- $v$ 满足 min-heap 的性质。
- 如果笛卡尔树的 $k,v$ 值确定,且 $k$ 互不相同,$v$ 互不相同,那么这个笛卡尔树的结构是唯一的。
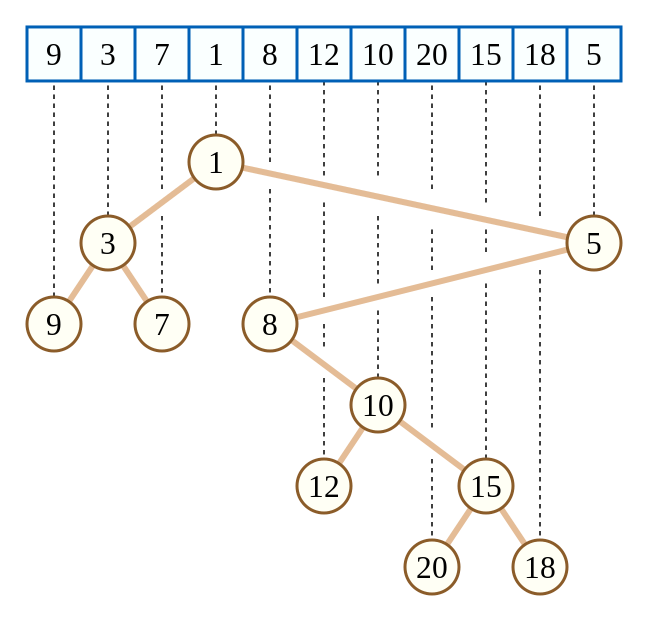
$O(n) 建树$
给定一个数组,可以建出对应的笛卡尔树,将数组的值作为 $v$,数组的index作为 $k$,建树的思想是:
每次取当前数组中最小的那个元素,将它左边作为左子树,右边作为右子树,然后递归建树。
通过单调栈维护从根出发的向右的链(递增栈),在加入一个新元素 $x$ 前(弹出过程已经完成):
- 如果之前有弹出元素,那么最后一个弹出的元素作为 $x$ 的左child。
- 如果此时栈上有元素,那么栈顶的元素的右 $child$ 是 $x$。
应用
笛卡尔树可以用于 $O(n)$ 或者 $O(n\log n)$ 建BST,见 例2
例1 洛谷P5854【模板】笛卡尔树
题意
给定一个 $1$ 到 $n$ 的permutation,构建出笛卡尔树。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e7+5;
struct Node {
int lc, rc, p, idx;
} a[maxn];
int n;
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].p;
a[i].idx = i;
}
stack<pii> st; // {val, idx},idx作为树Node的index
for (int i = 1; i <= n; i++) {
int last = 0;
while (st.size() && st.top().first > a[i].p) last = st.top().second, st.pop();
if (last) a[i].lc = last;
if (st.size()) a[st.top().second].rc = a[i].idx;
st.push({a[i].p, i});
}
ll ans1 = 0, ans2 = 0;
for (int i = 1; i <= n; i++) {
ans1 ^= ((ll)i * (a[i].lc + 1));
ans2 ^= ((ll)i * (a[i].rc + 1));
}
cout << ans1 << " " << ans2 << "\n";
}
例2 洛谷P1377 [TJOI2011] 树的序
题意
给定一个 $1$ 到 $n$ 的permutation,代表按照这个顺序将这些元素插入到一个 BST 中。
求所有能够生成同样BST的所有permutation中,字典序最小的一个。
其中,$n \leq 10^5$。
题解
很容易可以想到一个思路:按照给定的序列,把BST建出来,然后求这个BST的pre-order就是字典序最小的了(因为先访问左边,再访问右边,并且pre-order保证了结构一致,所以pre-order即是所求)。
现在问题来了:根据这个序列建BST,最坏情况下是 $O(n^2)$ 的,怎么加速?
注意到,根据一个序列建BST,得到的BST满足两个性质:
- 每个节点的 index 满足小根堆的性质:因为在BST中,一个 $u$ 的index一定比它的 parent 的index更加靠后。
- 每个节点的值 (value) 满足BST的性质:因为这就是一个BST。
回忆笛卡尔树的性质:
- 每个节点的 index 满足BST性质。
- 每个节点的 value 满足小根堆性质。
恰好是反过来的!
于是我们将原序列的 index 与 value 反过来,然后建立笛卡尔树,建好以后再反一次,就得到了想要的BST了。
• 由于这个题给定的 value 是 $1$ 到 $n$ 的排序,所以可以直接 $O(n)$ 反过来,否则需要 $O(n\log n)$。
• BST的根就是栈最底下的那个节点(因为我们维护的是一个从根开始向右的链)。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
struct Node {
int lc, rc, p, idx;
} a[maxn];
int idx_to_val[maxn], val_to_idx[maxn];
int n;
void dfs(int u) {
cout << idx_to_val[a[u].p] << " ";
if (a[u].lc) dfs(a[u].lc);
if (a[u].rc) dfs(a[u].rc);
}
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) {
int val; cin >> val;
idx_to_val[i] = val;
val_to_idx[val] = i;
a[i].idx = i;
a[val].p = i;
}
stack<pii> st;
for (int i = 1; i <= n; i++) {
int last = 0;
while (st.size() && st.top().first > a[i].p) last = st.top().second, st.pop();
if (last) a[i].lc = last;
if (st.size()) a[st.top().second].rc = a[i].idx;
st.push({a[i].p, i});
}
int rt = -1;
while (st.size()) rt = st.top().second, st.pop();
dfs(rt);
cout << "\n";
}
