线段树优化建图
Contents
介绍
线段树优化建图用于解决图中边数过多,不能直接建的问题。
直接看例题:
例1 CF786B. Legacy
题意
给定 $n$ 个点的有向带权图,初始状态下图中没有边。给定 $q$ 个操作。每次操作有 $3$ 种:
$1~u~v~w$:从 $u$ 向 $v$ 连一条权值为 $w$ 的边。
$2~u~l~r~w$:从 $u$ 向 $[l,r]$ 的所有点连一条权值为 $w$ 的边。
$3~u~l~r~w$:从 $[l,r]$ 的所有点向 $u$ 连一条权值为 $w$ 的边。
最后输出从点 $s$ 出发到其他所有点的最短路。
我们利用线段树优化建图。建一棵线段树,假设我们要从 $8$ 连向 $[3,7]$,则我们可以这样建:
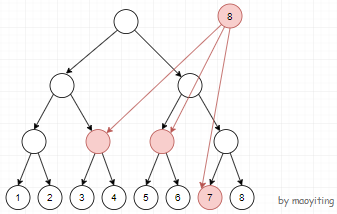
这样每次只需要建 $O(\log n)$ 条边。
其中,连出的粉色边拥有边权 $w$,而线段树上的边的边权均为 $0$,表达了从上面的节点可以无损耗的来到叶子节点(也就是原图中真正的节点)。
如果是从 $[3,7]$ 连向 $8$,则是反过来的。
但不能把这些边都建在同一棵树上,需要两棵线段树分别来表示这两种操作。
建立两棵线段树,一个的边是从上到下(叫 out-tree),一个的边是从下到上(叫 in-tree),而这些的线段树的叶子节点均代表原图中的节点。它们本质上是同一个节点,所以它们之间需要连权值为 $0$ 的双向边。
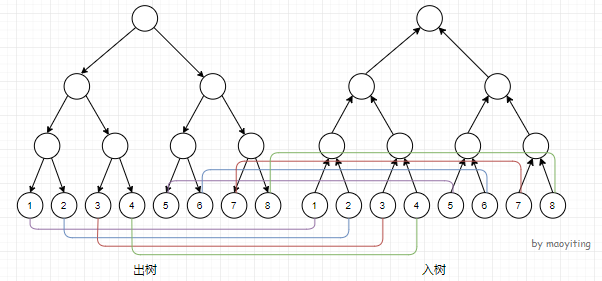
建好以后就可以连边了,无论是从区间连到点,还是从点连到区间,都是从in-tree出发,连到out-tree。其中,
- 区间 $\rightarrow$ 点:in-tree 的区间节点 $\rightarrow$ out-tree 的叶子节点。
- 点 $\rightarrow$ 区间:in-tree 的叶子节点 $\rightarrow$ out-tree 的区间节点。
最后怎么跑最短路呢?
实际上就是在这两棵线段树上跑,只不过除了原图中的点(叶子节点)以外,多了线段树上的一些点而已。我们就从任何一棵树的叶子节点 $s$ 出发,然后到任何一棵树的其他叶子节点的最短距离即是我们的最短路。本质上是给原图添加了一些辅助点。
• 写代码的时候用 u 和 u+N 区分两棵树上的节点,并且注意原图中的点对应的是叶子节点,所以编号不再是 1-n 了,用 inleaf[maxn], outleaf[maxn] 来记录编号。
时间复杂度:$O(m \log m) = O(n\log^2n)$,空间复杂度:$O(m) = O(n \log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+500;
struct Edge {
int u, v, w;
};
vector<Edge> adj[maxn];
struct Node {
int v; ll d;
bool operator<(const Node& other) const {
return d > other.d;
}
};
struct Dijkstra {
bool vis[maxn];
ll dis[maxn];
priority_queue<Node> pq;
void run(int x) {
memset(dis, -1, sizeof(dis));
memset(vis, 0, sizeof(vis));
pq.push({x, 0});
dis[x] = 0;
while (pq.size()) {
auto [u, d] = pq.top(); pq.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto [_, v, w] : adj[u]) {
if (dis[v] == -1 || dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
pq.push({v, dis[v]});
}
}
}
}
} di;
int n, q, s;
int N = 5e5;
void addEdge(int u, int v, int w) {
adj[u].push_back({u,v,w});
}
// [1...N] 是 out-tree的范畴,[N+1...2N] 是in-tree的范畴
int outleaf[maxn], inleaf[maxn];
void build(int cur, int l, int r) {
if (l == r) {
outleaf[l] = cur;
inleaf[l] = cur+N;
addEdge(outleaf[l], inleaf[l], 0);
addEdge(inleaf[l], outleaf[l], 0);
return;
}
int mid = (l+r) >> 1;
int lc = cur<<1, rc = lc|1;
addEdge(cur, lc, 0);
addEdge(cur, rc, 0);
addEdge(lc+N, cur+N, 0);
addEdge(rc+N, cur+N, 0);
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
}
// type = 1 单独处理了 (从 in->out 或者 反过来都没区别)
// type = 2: 从 u 连一条边到 [L,R],那么从 inleaf[u] -> out (N+1...2N -> 1...N)
// type = 3: 从 [L,R] 连一条边到 u,那么从 in -> outleaf[u] (N+1...2N -> 1...N)
// w 为权值
void add(int cur, int l, int r, int u, int L, int R, int w, int type) {
if (L <= l && R >= r) {
if (type == 2) addEdge(inleaf[u], cur, w);
else addEdge(cur+N, outleaf[u], w);
return;
}
int mid = (l+r) >> 1;
if (L <= mid) add(cur<<1, l, mid, u, L, R, w, type);
if (R > mid) add(cur<<1|1, mid+1, r, u, L, R, w, type);
}
int main() {
fastio;
cin >> n >> q >> s;
build(1, 1, n);
while (q--) {
int type; cin >> type;
if (type == 1) {
int u, v, w; cin >> u >> v >> w;
addEdge(inleaf[u], outleaf[v], w);
} else {
int u, L, R, w; cin >> u >> L >> R >> w;
add(1, 1, n, u, L, R, w, type);
}
}
di.run(inleaf[s]);
for (int i = 1; i <= n; i++) {
cout << di.dis[outleaf[i]] << " ";
}
cout << "\n";
}
例2 洛谷P6348 [PA2011] Journeys
题意
$n$ 个节点的无权无向图中,有 $m$ 条道路。
每条道路代表从 $[a,b]$ 都能走到 $[c,d]$。
给定出发点 $s$,求从 $s$ 出发到其他点的最短路。
其中,$n \leq 5 \times 10^5, m \leq 10^5$。
题解
几乎和上一道题一样,区别在于这次可以从区间连到区间了,而且是双向边。
把一个区间 $[a,b]$ 拆成线段树上的节点 $x_1,x_2,…,x_k$,然后把 $[c,d]$ 拆成 $y_1,y_2,…,y_l$。
然后对于每个 $i,j$,都连 $x_i \leftrightarrow y_j$。不过这样每次要连 $O(log^2 n)$ 条边,复杂度太高了。
可以建一个虚拟的点 $u$,然后将所有 $x_i \rightarrow u \rightarrow y_j$。由于是双向边,就再建一个 $v$,$y_j \rightarrow v \rightarrow x_i$。
这样复杂度又降回 $O(\log n)$ 了。
• 最后注意这是无权图,跑个 01-BFS 找最短路即可。
代码
#include <bits/stdc++.h>
using namespace std;
struct Edge {
int u, v, w;
};
vector<Edge> adj[maxn];
int n, m, s;
int N = 2e6;
void addEdge(int u, int v, int w) {
adj[u].push_back({u,v,w});
}
// [1...N] 是 out-tree的范畴,[N+1...2N] 是in-tree的范畴
int outleaf[maxn], inleaf[maxn];
void build(int cur, int l, int r) {
if (l == r) {
outleaf[l] = cur;
inleaf[l] = cur+N;
addEdge(outleaf[l], inleaf[l], 0);
addEdge(inleaf[l], outleaf[l], 0);
return;
}
int mid = (l+r) >> 1;
int lc = cur<<1, rc = lc|1;
addEdge(cur, lc, 0);
addEdge(cur, rc, 0);
addEdge(lc+N, cur+N, 0);
addEdge(rc+N, cur+N, 0);
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
}
void find_nodes(int cur, int l, int r, int L, int R, vector<int>& nodes) {
if (L <= l && R >= r) {
nodes.push_back(cur);
return;
}
int mid = (l+r) >> 1;
if (L <= mid) find_nodes(cur<<1, l, mid, L, R, nodes);
if (R > mid) find_nodes(cur<<1|1, mid+1, r, L, R, nodes);
}
int id = 0;
void add(int L1, int R1, int L2, int R2) {
vector<int> nodes1, nodes2;
find_nodes(1, 1, n, L1, R1, nodes1);
find_nodes(1, 1, n, L2, R2, nodes2);
int nd1 = 2*N + id + 1, nd2 = 2*N + id + 2;
id += 2;
for (int x : nodes1) {
addEdge(x+N, nd1, 1);
addEdge(nd2, x, 1);
}
for (int y : nodes2) {
addEdge(nd1, y, 1);
addEdge(y+N, nd2, 1);
}
}
deque<int> q;
int dis[maxn];
bool vis[maxn];
void bfs01(int x) {
memset(dis, -1, sizeof(dis));
q.push_back(x);
dis[x] = 0;
while (q.size()) {
int u = q.front(); q.pop_front();
if (vis[u]) continue;
vis[u] = 1;
for (auto [_, v, w] : adj[u]) {
if (dis[v] == -1 || dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (w == 0) q.push_front(v);
else q.push_back(v);
}
}
}
}
int main() {
fastio;
cin >> n >> m >> s;
build(1, 1, n);
while (m--) {
int a, b, c, d; cin >> a >> b >> c >> d;
add(a, b, c, d);
}
bfs01(inleaf[s]);
for (int i = 1; i <= n; i++) {
cout << dis[outleaf[i]] / 2 << "\n";
}
}
例3 洛谷P5025 [SNOI2017] 炸弹
题意
在一条直线上有 $n$ 个炸弹,每个炸弹的坐标是 $x_i$,爆炸半径是 $r_i$。
当一个炸弹 $i$ 爆炸时,如果另一个炸弹 $j$ 满足 $|x_j-x_i| \leq r_i$,那么炸弹 $j$ 也会被引爆。
对于每一个 $i$,计算如果一开始引爆 $i$,将会有多少个炸弹被引爆,设这个值为 $k_i$,计算 $\sum\limits_{i=1}^n i*k_i$。
其中,$n \leq 5 \times 10^5, |x_i| \leq 10^{18}, r_i \in [0, 2\times 10^{18}]$。
题解
显然,一个炸弹 $i$ 被引爆后,一定影响的是以它为中心的一个区间的范围。那么可以用二分求出这个区间,然后线段树优化建图来连边。
建完边以后,相当于给定一个图,问从每一个节点出发,能到达多少个节点?
那么可以先SCC缩点,得到一个DAG,然后在DAG上跑dp。
但DAG上的dp其实有一个问题,见下图:
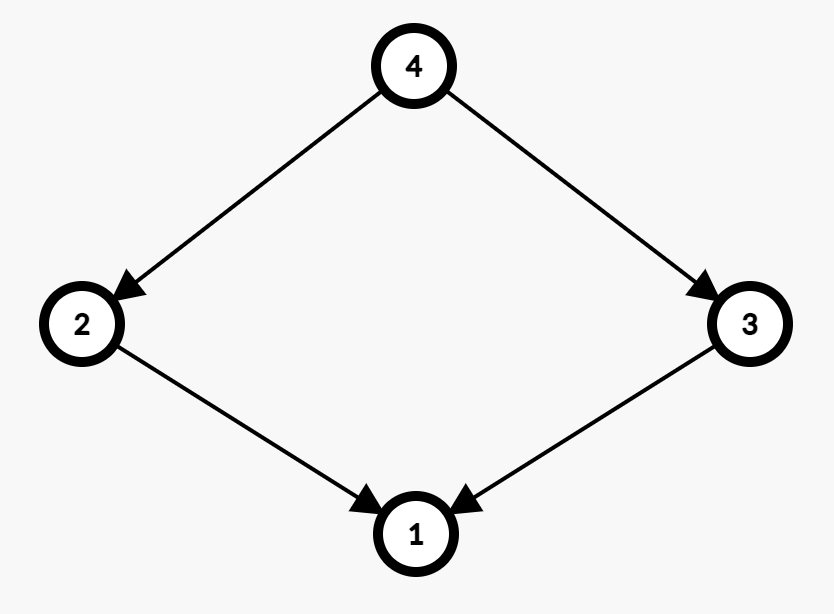
节点 $2$ 和 $3$ 可到达的数量均为 $2$,但这样的话节点 $4$ 可到达的数量就会变成 $5$,因为节点 $1$ 被统计了两次。
并没有什么好办法来处理这个问题,但我们注意到,初始情况下引爆一个炸弹,最后的影响范围一定是一个区间。
于是 dp 值维护的是能够影响到的区间左端点和右端点,而不是影响到的节点数量,这样就没有这个问题了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e6+50000;
vector<int> adj[maxn];
struct Node {
int v; ll d;
bool operator<(const Node& other) const {
return d > other.d;
}
};
int n;
int N = 2e6;
void addEdge(int u, int v) {
adj[u].push_back(v);
}
// [1...N] 是 out-tree的范畴,[N+1...2N] 是in-tree的范畴
int outleaf[maxn], inleaf[maxn];
void build(int cur, int l, int r) {
if (l == r) {
outleaf[l] = cur;
inleaf[l] = cur+N;
addEdge(outleaf[l], inleaf[l]);
addEdge(inleaf[l], outleaf[l]);
return;
}
int mid = (l+r) >> 1;
int lc = cur<<1, rc = lc|1;
addEdge(cur, lc);
addEdge(cur, rc);
addEdge(lc+N, cur+N);
addEdge(rc+N, cur+N);
build(cur<<1, l, mid);
build(cur<<1|1, mid+1, r);
}
void add(int cur, int l, int r, int u, int L, int R) {
if (L <= l && R >= r) {
addEdge(inleaf[u], cur);
return;
}
int mid = (l+r) >> 1;
if (L <= mid) add(cur<<1, l, mid, u, L, R);
if (R > mid) add(cur<<1|1, mid+1, r, u, L, R);
}
// from[u] 代表 u 所在的SCC编号,scc代表scc编号,sz[scc] 代表对应scc的大小
struct Tarjan {
int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn];
bool in[maxn]; // instack or not
int st[maxn], tail = -1;
void dfs(int u) {
in[u] = 1;
st[++tail] = u;
dfn[u] = low[u] = ++id;
for (int to : adj[u]) {
if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]); // 要记得在栈内
if (!dfn[to]) {
dfs(to);
low[u] = min(low[u], low[to]);
}
}
if (dfn[u] == low[u]) {
from[u] = ++scc;
sz[scc] = 1;
while (tail >= 0 && st[tail] != u) {
int cur = st[tail];
from[cur] = from[u];
sz[scc]++;
tail--;
in[cur] = 0; // 记得这里,将在栈中的标记去掉
}
tail--;
in[u] = 0; // 记得这里,将在栈中的标记去掉
}
}
// 跑tarjan
void solve() {
for (int i = 1; i <= N*2; i++) {
if (!dfn[i]) dfs(i);
}
}
} tj;
struct Graph {
int n;
vector<int> adj[maxn];
int w[maxn], deg[maxn];
pii dp[maxn];
void addEdge(int u, int v) {
adj[u].push_back(v);
}
void remove_dup() {
for (int i = 1; i <= n; i++) {
sort(adj[i].begin(), adj[i].end());
adj[i].resize(unique(adj[i].begin(), adj[i].end()) - adj[i].begin());
for (int v : adj[i]) deg[v]++; // 注意重边,所以不能在addEdge的时候统计deg,得先去重
}
}
vector<int> seq; // 拓扑排序的逆序列
void topo() {
vector<int> q;
for (int i = 1; i <= n; i++) {
if (!deg[i]) q.push_back(i);
}
while (q.size()) {
int u = q.back();
q.pop_back();
for (int v : adj[u]) {
deg[v]--;
if (deg[v] == 0) {
q.push_back(v);
}
}
seq.push_back(u);
}
reverse(seq.begin(), seq.end());
}
void run_dp() {
for (int u : seq) {
for (int v : adj[u]) {
dp[u].first = min(dp[u].first, dp[v].first);
dp[u].second = max(dp[u].second, dp[v].second);
}
}
}
} graph;
struct Bomb {
ll x, r;
int id;
bool operator<(const Bomb& other) const {
return x < other.x;
}
} a[maxn];
int main() {
fastio;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].r, a[i].id = i;
sort(a+1, a+n+1);
build(1, 1, n);
for (int i = 1; i <= n; i++) {
int l = lower_bound(a+1, a+i+1, Bomb {a[i].x - a[i].r, 0, 0}) - a;
int r = prev(upper_bound(a+i+1, a+n+1, Bomb {a[i].x + a[i].r, 0, 0})) - a;
add(1, 1, n, i, l, r);
}
tj.solve();
for (int i = 1; i <= N*2; i++) {
for (int j : adj[i]) {
int fu = tj.from[i], fv = tj.from[j];
if (fu == fv) continue;
graph.addEdge(fu, fv);
}
}
graph.n = tj.scc;
for (int i = 1; i <= graph.n; i++) graph.dp[i] = {1e9, -1};
for (int i = 1; i <= n; i++) {
int u = tj.from[inleaf[i]];
graph.dp[u].first = min(graph.dp[u].first, i);
graph.dp[u].second = max(graph.dp[u].second, i);
}
graph.remove_dup();
graph.topo();
graph.run_dp();
Z ans = 0;
for (int i = 1; i <= n; i++) {
Z res = 0;
int from = tj.from[inleaf[i]];
ll num = graph.dp[from].second - graph.dp[from].first + 1;
res = num * a[i].id;
ans += res;
}
cout << ans << endl;
}
