扫描线 - tom0727's blog

介绍

扫描线是一种思想，本质上是利用了线段树。可以用来处理矩形面积并，矩形周长并等经典问题。

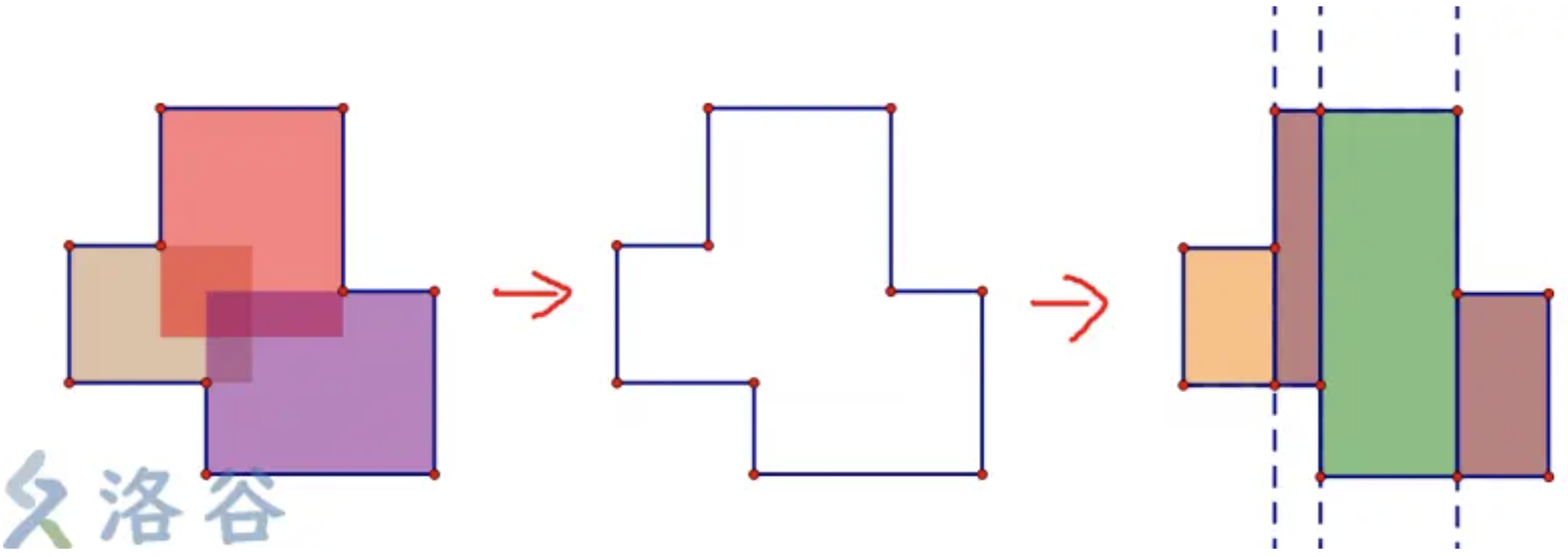
如图，我们用一条竖着的线从左到右扫描。我们将每一个矩形的左右两个边分别拿出来，作为两个线段。并且我们用一颗线段树维护 $y$ 坐标，这样一个线段覆盖的就是一个 $y$ 坐标的区间了（注意 $y$ 坐标需要离散化）。

同时注意到，左边是入边，象征着一个矩形开始了，右边是出边，象征着这个矩形结束了，所以我们给入边赋权值 $+1$，而给出边赋权值 $-1$，对应在线段树上给一个区间全部 $+1$ 或者 $-1$。

然后将所有的线段按照其 $x$ 坐标进行 sort，然后每次扫到一个线段，就更新线段树，并且和前一个线段树的 $x$ 坐标差 $(x_i - x_{i-1})$ 就可以作为这段矩形的宽了，然后询问当前线段树的 $y$ 坐标有多少被覆盖（权值 $>0$）即可得到这段的面积贡献。

注意事项

实现的时候需要注意，线段树的节点维护的应该是原图形中的 “线段“，而不是 ”点“，如果维护的是点的话，那么 $[1,1]$ 这种对应的只有一个点，没有任何意义。例如 $y$ 坐标离散化后为 $[1,2,3,4]$，那么线段树应该只有 $1,2,3$ 这三个节点，分别代表了 $[1,2], [2,3], [3,4]$ 这三个区间，换言之在线段树上的 $[i,j]$ 对应了原矩形 $y$ 坐标的 $[i,j+1]$。
线段树中需要利用到区间更新，区间查询。但是由于一个矩形一定是入边先到，然后才是出边，所以并不需要 push_down()，直接对 flag 本身进行操作即可。
注意下面代码中的实现，在叶子节点也调用了 push_up()，所以空间需要额外开个 $2$ 倍。
代码中不要使用 x1, y1 之类的变量名，和 std 冲突了。

模版（矩形面积并）

#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5+5;  // 注意原题数据范围为 1e5, 需要额外开 2倍空间

map<int, int> mp;
int rev_mp[maxn];
struct SegmentTree {
    struct Node {
        ll sum;
        int flag;
    } tr[maxn<<2];
    void build(int cur, int l, int r) {
        tr[cur].sum = tr[cur].flag = 0;
        if (l == r) return;
        int mid = (l+r) >> 1;
        build(cur<<1, l, mid);
        build(cur<<1|1, mid+1, r);
    }
    void push_up(int cur, int l, int r) {
        if (tr[cur].flag) tr[cur].sum = rev_mp[r+1] - rev_mp[l];
        else tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum;
    }
    void update(int cur, int l, int r, int L, int R, int X) {
        if (L <= l && R >= r) {
            tr[cur].flag += X;
            push_up(cur, l, r);
            return;
        }
        int mid = (l+r) >> 1;
        if (L <= mid) update(cur<<1, l, mid, L, R, X);
        if (R > mid) update(cur<<1|1, mid+1, r, L, R, X);
        push_up(cur, l, r);
    }
} tr;

struct Line {
    int X, Y1, Y2, flag;
    bool operator<(const Line& other) const {
        return tuple {X, -flag} < tuple {other.X, -other.flag};
    }
} l[maxn];

int n, X1[maxn], Y1[maxn], X2[maxn], Y2[maxn];
int main() {
    cin >> n;
    set<int> se;
    for (int i = 1; i <= n; i++) cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i], se.insert(Y1[i]), se.insert(Y2[i]);
    int N = 0;
    for (int X : se) mp[X] = ++N, rev_mp[N] = X;
    for (int i = 1; i <= n; i++) {
        l[i*2 - 1] = {X1[i], Y1[i], Y2[i], 1};
        l[i*2] = {X2[i], Y1[i], Y2[i], -1};
    }
    sort(l+1, l+2*n+1);

    ll ans = 0;
    for (int i = 1; i <= 2*n; i++) {
        ans += tr.tr[1].sum * (l[i].X - l[i-1].X);
        tr.update(1, 1, N-1, mp[l[i].Y1], mp[l[i].Y2]-1, l[i].flag);
    }
    cout << ans << endl;
}

例题

例2 洛谷P1856 [IOI1998] 矩形周长Picture

题意

给定 $n$ 个矩形，求它们并起来的图形的周长。

其中，$n \leq 5000$，坐标数据范围在 $[-10^4, 10^4]$。

题解

注意到，用一条竖线从左往右扫，其实计算的是矩形的横边的长。那么我们如何知道在扫描过程中，当前有几条横边？

显然，扫描过程中，有 $x$ 条独立的竖线段，就有 $2x$ 条横边。

所以我们在线段树上维护有多少条独立的竖着的线段，并且支持加入/减去一条线段即可。

这个在每个节点里面维护其最右端和最左端是否被覆盖即可，如果覆盖的话相当于这个区间内的线段少了一条，因为左child的右端点和右child的左端点分别被两条线段覆盖，说明这两条线段可以合并。

• 这题还需要从下往上再扫一边，来计算竖边的长。不过写起来很简单，把 $x,y$ 坐标颠倒一下即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
const int maxm = 2e5+500;

map<int, int> mp;
int rev_mp[maxn];
struct SegmentTree {
    struct Node {
        ll sum;
        int flag;
        int l, r;  // 左边被覆盖，右边被覆盖
    } tr[maxn<<2];
    void build(int cur, int l, int r) {
        tr[cur].sum = tr[cur].flag = tr[cur].l = tr[cur].r = 0;
        if (l == r) return;
        int mid = (l+r) >> 1;
        build(cur<<1, l, mid);
        build(cur<<1|1, mid+1, r);
    }
    void push_up(int cur) {
        if (tr[cur].flag) tr[cur].sum = tr[cur].l = tr[cur].r = 1;
        else {
            tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum - (tr[cur<<1].r && tr[cur<<1|1].l);
            tr[cur].l = tr[cur<<1].l;
            tr[cur].r = tr[cur<<1|1].r;
        }

    }
    void update(int cur, int l, int r, int L, int R, int x) {
        if (L <= l && R >= r) {
            tr[cur].flag += x;
            push_up(cur);
            return;
        }
        int mid = (l+r) >> 1;
        if (L <= mid) update(cur<<1, l, mid, L, R, x);
        if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
        push_up(cur);
    }
} tr;
struct LineX {
    int X, Y1, Y2, flag;
} l[maxn];

int n, X1[maxn], Y1[maxn], X2[maxn], Y2[maxn];
int main() {
    cin >> n;
    set<int> se;
    for (int i = 1; i <= n; i++) cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i], se.insert(Y1[i]), se.insert(Y2[i]);
    int N = 0;
    for (int X : se) mp[X] = ++N, rev_mp[N] = X;
    for (int i = 1; i <= n; i++) {
        l[i*2 - 1] = {X1[i], Y1[i], Y2[i], 1};
        l[i*2] = {X2[i], Y1[i], Y2[i], -1};
    }
    sort(l+1, l+2*n+1, [](auto a, auto b) {
        return tuple {a.X, a.flag} < tuple {b.X, b.flag};
    });
    ll ans = 0;
    for (int i = 1; i <= 2*n; i++) {
        ans += tr.tr[1].sum * (l[i].X - l[i-1].X);
        tr.update(1, 1, N-1, mp[l[i].Y1], mp[l[i].Y2]-1, l[i].flag);
    }
    
    se.clear();
    mp.clear();
    for (int i = 1; i <= n; i++) se.insert(X1[i]), se.insert(X2[i]);
    N = 0;
    for (int x : se) mp[x] = ++N, rev_mp[N] = x;
    for (int i = 1; i <= n; i++) {
        l[i*2 - 1] = {Y1[i], X1[i], X2[i], 1};
        l[i*2] = {Y2[i], X1[i], X2[i], -1};
    }
    sort(l+1, l+2*n+1, [](auto a, auto b) {
        return tuple {a.X, a.flag} < tuple {b.X, b.flag};
    });
    tr.build(1, 1, N-1);
    for (int i = 1; i <= 2*n; i++) {
        ans += tr.tr[1].sum * (l[i].X - l[i-1].X);
        tr.update(1, 1, N-1, mp[l[i].Y1], mp[l[i].Y2]-1, l[i].flag);
    }
    cout << ans*2 << endl;
}

例3 洛谷P3755 [CQOI2017] 老C的任务

题意

二维平面上给定 $n$ 个点，每个点位于 $(x_i,y_i)$，有一个权值 $p_i$。

有 $m$ 次询问，每次询问一个矩阵 $x_1,y_1,x_2,y_2$，询问矩阵内（包括边界）的点的权值和。

其中，$n,m \leq 10^5, x,y \in [-2^{31}, 2^{31}]$。

题解

虽然和扫描线并没有什么关系，但是思想有点类似。

这一类二维数点问题，都可以转化为二维偏序问题。

如果是在线可以用树套树，离线的话可以用线段树。

怎么偏序呢？注意到询问 $x_1,y_1,x_2,y_2$，本质上可以用二维前缀和拆成 $4$ 个不同的询问

$$(x_2,y_2), (x_1-1,y_2), (x_2,y_1-1), (x_1-1,y_1-1)$$

每次询问有哪些点在它的左下方，也就是询问 $(x,y)$ 的数量使得 $x \leq x_2, y \leq y_2$ 等等（这题是权值和，但本质一样）。

这样就好偏序了，离散化所有的 $x,y$ 坐标（记得 $x,y$ 分开离散化，并且询问也要离散化进去），然后将询问根据 $x$ 坐标一存，然后从左往右加点进线段树/树状数组即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5+5;
const int maxm = 2e5+500;

struct Node {
    int x, y;
    ll p;
} a[maxn];
struct Query {
    int x1, y1, x2, y2;
} q[maxn];
struct Ask {
    int x, y, id, flag;
};
vector<Ask> adj[maxn];
vector<Node> points[maxn];

set<int> sx, sy;
map<int, int> mx, my;

struct SegmentTree {
    struct Node {
        ll sum, tag;
    };
    Node tr[maxn<<2];
    void push_up(int cur) {
        tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum;
    }
    void push_down(int cur, int l, int r) {
        if (!tr[cur].tag) return;
        ll tag = tr[cur].tag;
        tr[cur].tag = 0;
        int lc = cur<<1, rc = lc + 1;
        int mid = (l+r) >> 1;
        tr[lc].sum += tag * (mid-l+1);
        tr[rc].sum += tag * (r-mid);
        tr[lc].tag += tag;
        tr[rc].tag += tag;
    }
    void update(int cur, int l, int r, int L, int R, ll x) {
        if (L <= l && R >= r) {
            tr[cur].tag += x;
            tr[cur].sum += x * (r-l+1);
            return;
        }
        push_down(cur, l, r);
        int mid = (l+r) >> 1;
        if (L <= mid) update(cur<<1, l, mid, L, R, x);
        if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
        push_up(cur);
    }
    void update(int cur, int l, int r, int p, ll x) {
        if (l == r) {
            tr[cur].sum += x; return;
        }
        push_down(cur, l, r);
        int mid = (l+r) >> 1;
        if (p <= mid) update(cur<<1, l, mid, p, x);
        else update(cur<<1|1, mid+1, r, p, x);
        push_up(cur);
    } 
    ll query(int cur, int l, int r, int L, int R) {
        if (l >= L && r <= R) return tr[cur].sum;
        push_down(cur, l, r);
        int mid = (l+r) >> 1;
        ll res = 0;
        if (L <= mid) res += query(cur<<1, l, mid, L, R);
        if (R > mid) res += query(cur<<1|1, mid+1, r, L, R);
        push_up(cur);
        return res;
    }
} tr;

int n, m;
ll ans[maxn];
int main() {
    fastio;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y >> a[i].p, sx.insert(a[i].x), sy.insert(a[i].y);
    for (int i = 1; i <= m; i++) {
        cin >> q[i].x1 >> q[i].y1 >> q[i].x2 >> q[i].y2;
        sx.insert(q[i].x2); sx.insert(q[i].x1-1);
        sy.insert(q[i].y2); sy.insert(q[i].y1-1);
    }
    int id = 0;
    for (int i : sx) mx[i] = ++id;
    id = 0;
    for (int i : sy) my[i] = ++id;
    for (int i = 1; i <= n; i++) {
        a[i].x = mx[a[i].x], a[i].y = my[a[i].y];
        int x = a[i].x, y = a[i].y;
        points[x].push_back({a[i]});
    }
    for (int i = 1; i <= m; i++) {
        int X1 = mx[q[i].x1 - 1], X2 = mx[q[i].x2], Y1 = my[q[i].y1 - 1], Y2 = my[q[i].y2];
        adj[X2].push_back({X2, Y2, i, 1});
        adj[X2].push_back({X2, Y1, i, -1});
        adj[X1].push_back({X1, Y2, i, -1});
        adj[X1].push_back({X1, Y1, i, 1});
    }

    int N = sx.size(), M = sy.size();
    for (int i = 1; i <= N; i++) {
        for (auto [x, y, p] : points[i]) {
            tr.update(1, 1, M, y, p);
        }
        for (auto [x, y, id, flag] : adj[i]) {
            assert(x == i);
            ans[id] += tr.query(1, 1, M, 1, y) * flag;
        }
    }
    for (int i = 1; i <= m; i++) cout << ans[i] << "\n";
}

例4 洛谷P1502 窗口的星星

题意

给定 $n$ 个点，坐标为 $(x_i,y_i)$ 并且带一个权值 $L_i$。

现在需要用一个宽为 $W$，高为 $H$ 的矩形框起一些点，使得这些点的权值和最大。矩形边框上的点不计入。

注意这个矩形所在的坐标可以是小数。

其中，$n \leq 10^4, W,H \leq 10^6, x_i, y_i \in [0,2^{31}]$。

题解

对于每个点 $(x,y)$，考虑我们矩形的右上角在哪。如果计入边框，那么矩形的右上角只需要在 $(x,y)$ 到 $(x+W,y+H)$，就能覆盖到这个点。

既然矩形所在位置可以是小数，且边框不计入，那么我们直接将这个矩形的长宽各减去 $0.5$。

这样本来从 $(x,y)$ 作为左下角的，覆盖到的范围就是 $(x,y)$ 到 $(x+W-1,y+H-1)$ 了（包括边框）。

那么这个问题转化为：

将每个点 $(x,y)$ 看作一个带权值 $L$ 的矩形 $[x, x+W-1] \times [y, y+H-1]$，求平面上哪个点的权值最大？

那这就是一个标准的扫描线问题了，线段树维护最大值，进边加入线段树，出边减去线段树即可。

（甚至比面积并还好写，因为这次线段树维护的确确实实是点的坐标，而不是线段了）

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;

map<int, int> mp;
int rev_mp[maxn];
struct SegmentTree {
    struct Node {
        ll mx;
        ll flag;
    } tr[maxn<<2];
    void build(int cur, int l, int r) {
        tr[cur].mx = tr[cur].flag = 0;
        if (l == r) return;
        int mid = (l+r) >> 1;
        build(cur<<1, l, mid);
        build(cur<<1|1, mid+1, r);
    }
    void push_up(int cur) {
        tr[cur].mx = max(tr[cur<<1].mx, tr[cur<<1|1].mx);
    }
    void push_down(int cur) {
        if (!tr[cur].flag) return;
        ll f = tr[cur].flag;
        tr[cur].flag = 0;
        tr[cur<<1].mx += f, tr[cur<<1].flag += f;
        tr[cur<<1|1].mx += f, tr[cur<<1|1].flag += f;
    }
    void update(int cur, int l, int r, int L, int R, int x) {
        if (L <= l && R >= r) {
            tr[cur].mx += x;
            tr[cur].flag += x;
            return;
        }
        push_down(cur);
        int mid = (l+r) >> 1;
        if (L <= mid) update(cur<<1, l, mid, L, R, x);
        if (R > mid) update(cur<<1|1, mid+1, r, L, R, x);
        push_up(cur);
    }
} tr;

struct Line {
    int x, y1, y2, flag;
} l[maxn];

int n, X1[maxn], Y1[maxn], X2[maxn], Y2[maxn];

void solve() {
    int n, W, H; cin >> n >> W >> H;
    set<int> se;
    mp.clear();
    for (int i = 1; i <= n; i++) {
        int x, y, L; cin >> x >> y >> L;
        l[i*2 - 1] = {x, y, y+H-1, L};
        l[i*2] = {x+W, y, y+H-1, -L};
        se.insert(y);
        se.insert(y+H-1);
    }
    int N = 0;
    for (int x : se) mp[x] = ++N, rev_mp[N] = x;
    sort(l+1, l+2*n+1, [](auto a, auto b) {
        return tuple {a.x, a.flag} < tuple {b.x, b.flag};
    });
    tr.build(1, 1, N);
    ll ans = 0;
    for (int i = 1; i <= 2*n; i++) {
        tr.update(1, 1, N, mp[l[i].y1], mp[l[i].y2], l[i].flag);
        ans = max(ans, tr.tr[1].mx);
    }
    cout << ans << endl;
}


int main() {
    int T; cin >> T;
    while (T--) {
        solve();
    }
}

Contents

介绍

例题

例2 洛谷P1856 [IOI1998] 矩形周长Picture

例3 洛谷P3755 [CQOI2017] 老C的任务

例4 洛谷P1502 窗口的星星