Splay
Contents
介绍
Splay 是一种自平衡的 BST(二叉搜索树)。
模版
代码
struct Splay {
struct Node {
int par, child[2], sz, cnt;
ll val, flag;
} tr[maxn];
int rt, id = 0;
void push_up(int cur) {
if (!cur) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
tr[cur].sz = tr[lc].sz + tr[rc].sz + tr[cur].cnt;
}
void push_down(int cur) {
if (!cur || !tr[cur].flag) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
ll f = tr[cur].flag;
tr[lc].flag += f, tr[rc].flag += f;
tr[lc].val += f, tr[rc].val += f;
tr[cur].flag = 0;
}
void clear(int cur) {
tr[cur].par = tr[cur].val = tr[cur].sz = tr[cur].cnt = tr[cur].child[0] = tr[cur].child[1] = 0;
}
bool isright(int cur) {
return cur == tr[tr[cur].par].child[1];
}
void rotate(int x) {
if (!x || x == rt) return;
int y = tr[x].par, z = tr[y].par;
push_down(y); push_down(x); // 注意先 push_down parent
bool r = isright(x); // 注意这里, 是先 push_down 之后,才判断 isright(x) 的
tr[y].child[r] = tr[x].child[r^1];
if (tr[x].child[r^1]) tr[tr[x].child[r^1]].par = y;
tr[x].child[r^1] = y;
tr[y].par = x;
tr[x].par = z;
if (z) tr[z].child[y == tr[z].child[1]] = x;
push_up(y); push_up(x);
}
void splay(int x, int tar = 0) {
assert(x != 0);
while (tr[x].par != tar) {
int y = tr[x].par, z = tr[y].par;
if (z != tar) {
if (isright(y) == isright(z)) rotate(y);
else rotate(x);
}
rotate(x);
}
if (tar == 0) rt = x;
}
void insert(ll val) {
if (!rt) {
tr[++id].val = val;
tr[id].cnt++;
rt = id;
push_up(id);
return;
}
int cur = rt, p = 0;
while (1) {
push_down(cur);
if (tr[cur].val == val) {
tr[cur].cnt++;
push_up(cur);
push_up(p);
splay(cur);
break;
}
p = cur;
cur = tr[p].child[tr[p].val < val];
if (!cur) {
cur = ++id;
tr[cur].val = val;
tr[cur].cnt++;
tr[cur].par = p;
tr[p].child[tr[p].val < val] = cur;
push_up(cur);
push_up(p);
splay(cur);
break;
}
}
}
int query_rank(int x) { // 查询 x 所在的rank
splay(find(x));
return tr[tr[rt].child[0]].sz + 1;
}
int kth(int k) { // 查询第k大 (注意返回的是节点编号,不是值)
int cur = rt;
assert(cur != 0);
while (1) {
push_down(cur); // pushdown
int lc = tr[cur].child[0], rc = tr[cur].child[1];
if (lc && k <= tr[lc].sz) {
cur = lc;
} else {
k -= (tr[cur].cnt + tr[lc].sz);
if (k <= 0) {
return cur;
}
cur = rc;
}
}
}
int find(ll x) {
// 找一个值为 x 的节点,如果找不到就寻找最近的一个(可大可小)
int cur = rt;
while (tr[cur].child[tr[cur].val < x] && tr[cur].val != x) {
push_down(cur);
cur = tr[cur].child[tr[cur].val < x];
}
return cur;
}
int pre() {
int cur = tr[rt].child[0];
if (!cur) return cur;
while (tr[cur].child[1]) cur = tr[cur].child[1];
splay(cur);
return cur;
}
int nxt() {
int cur = tr[rt].child[1];
if (!cur) return cur;
while (tr[cur].child[0]) cur = tr[cur].child[0];
splay(cur);
return cur;
}
void del(ll val) {
splay(find(val)); // 将它旋转到根
if (tr[rt].cnt > 1) {
tr[rt].cnt--;
push_up(rt);
return;
}
int lc = tr[rt].child[0], rc = tr[rt].child[1];
if (!lc && !rc) {
clear(rt);
rt = 0;
return;
}
if (!lc || !rc) {
int tmp = rt;
if (!lc) rt = rc;
else rt = lc;
tr[rt].par = 0;
clear(tmp);
return;
}
int tmp = rt, cur = pre(), splay(cur); // 现在 cur 变为根了
tr[tr[tmp].child[1]].par = cur;
tr[cur].child[1] = tr[tmp].child[1];
clear(tmp);
push_up(rt);
}
int find_pre(ll val) { // 查询前驱所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val < val) return rt;
else return pre();
}
int find_nxt(ll val) { // 查询后继所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val > val) return rt;
else return nxt();
}
} tr;
int main() {
int n; cin >> n;
while (n--) {
int op, x; cin >> op >> x;
if (op == 1) tr.insert(x);
if (op == 2) tr.del(x);
if (op == 3) cout << tr.query_rank(x) << endl;
if (op == 4) {
int cur = tr.kth(x);
cout << tr.tr[cur].val << endl;
tr.splay(cur);
}
if (op == 5) {
int p = tr.find_pre(x);
cout << tr.tr[p].val << endl;
}
if (op == 6) {
int p = tr.find_nxt(x);
cout << tr.tr[p].val << endl;
}
}
}
数据结构操作
push_up
维护一个节点的信息,和线段树里的 push_up 没有区别。一般一个节点维护的是 par,child[2],以及 val(这个节点里储存的值),sz(这个节点对应的子树内的值的数量,包括重复的),cnt(这个节点储存的值出现的次数)。
• splay 本质是 multiset,所以可以储存重复值。
旋转
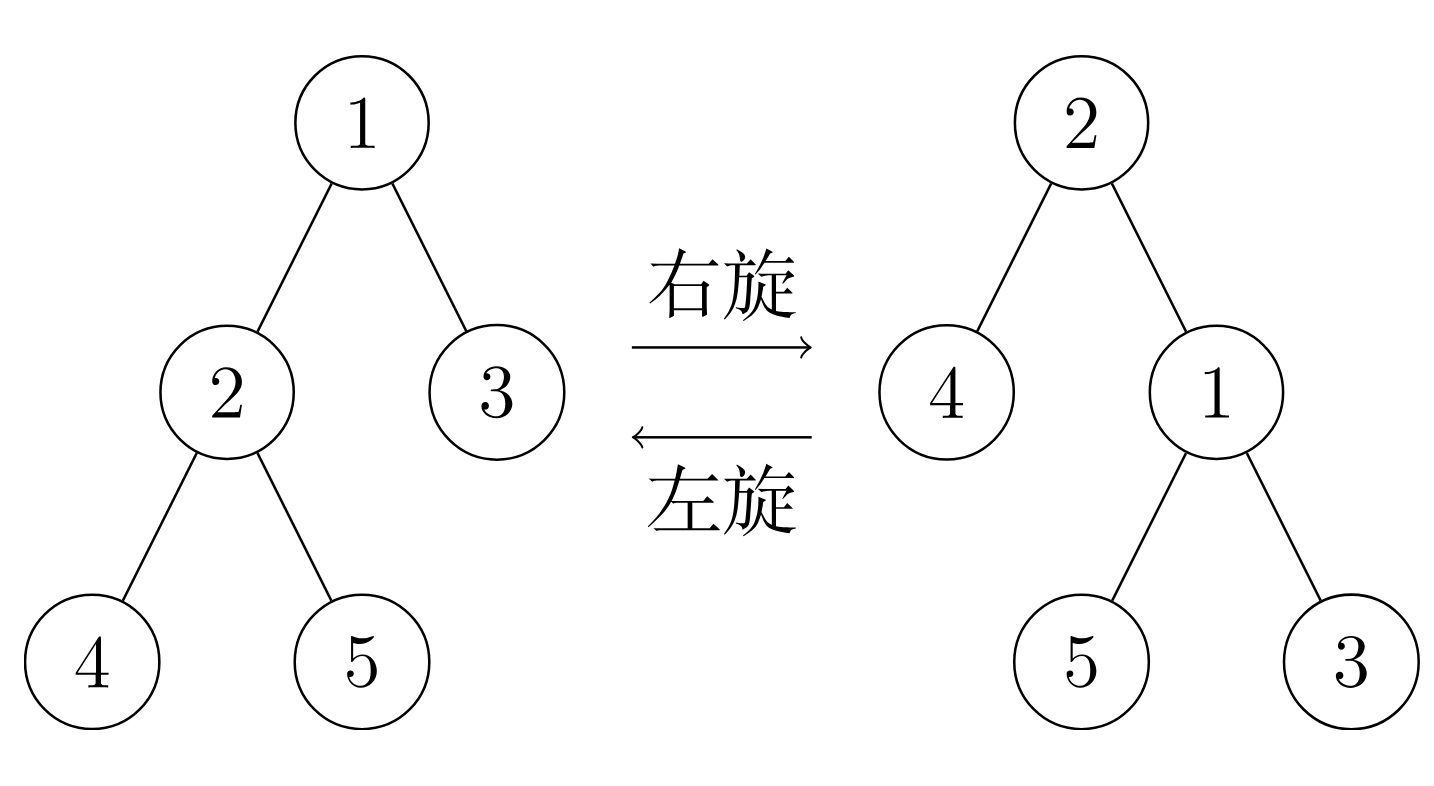
如图,对左图的节点 $2$ 进行右旋可以得到右图,而对于右图的节点 $1$ 进行左旋可以得到左图。
对节点 $x$ 进行旋转本质上就是旋转了它的parent $p$,让 $x$ 变成根,至于这次旋转是左旋还是右旋,则根据 $x$ 是 $p$ 的左儿子还是右儿子决定。
旋转时需要继承儿子,例如上图的节点 $5$,在左图是 $2$ 的右儿子,旋转后变成了 $1$ 的左儿子,这个继承儿子的过程不难想,思考一下即可。
• 有趣的是,无论怎么旋转,树的 in-order 始终不变。
Splay
Splay 操作是让一个节点旋转至根(或者是旋转 $x$ 直到其成为某一个目标节点 $tar$ 的直接儿子)。
在 Splay 树的设计中,每次访问一个节点 $x$ 后都要将其旋转至根节点。
分为两种情况:
-
如果 $x$ 离根节点就差一层了,意味着 $x$ 的parent就是
rt,那么直接旋转一次即可。 -
如果 $x$ 离节点差至少 $2$ 层,那么考虑其 parent $p$,分为两种情况:
2.1. $x$ 和 $p$ 均为其parent的左/右儿子,那么先旋转 $p$,再旋转 $x$。
2.2. $x$ 和 $p$ 一个是其parent的左儿子,一个是右儿子,那么旋转 $x$ 两次。
插入
插入一个值 $x$ 时,先在树中找到 $x$ 所在的节点,如果找到了直接 cnt++ 然后 pushup 一下即可。
如果没找到,就按照 BST 的性质一直往下,直到来到一个空的节点,然后在这个位置插入。
无论什么情况,插入后都记得要 push_up(cur), push_up(p), splay(cur)。
查找 $x$
和插入本质一样,按照 BST 的性质来即可。
如果没找到的话,返回的 node index 所对应的 node value 可能比 $x$ 大,或者小,但无论如何一定是离 $x$ 最近的(如果是大,那么就是后继,如果是小,那么就是前驱)。
• 由于查找后不一定要 splay,如例$2$ 里面,所以可以在外面 splay。
查询 $x$ 的排名
$x$ 的排名 = 树中$<x$ 的值的数量 $+1$。
那本质上就是一个查找以后,splay到根,然后返回根的 左child的 size + 1 即可。
查询第 $k$ 大的数
按照节点的左子树的 size,一路顺着左/右节点走即可。
• 注意,kth() 是唯一一个查询时,和节点本身的值无关,仅与其 size 有关的函数。
查询 $x$ 的前驱
一个查找 $x$ 以后 splay 到根,如果根的值比 $x$ 本身的小,它就是前驱,否则的话,在 $x$ 的左子树里找到最大值(进入左子树以后一直往右走即可)。
查询 $x$ 的后继
一个查找 $x$ 以后 splay 到根,如果根的值比 $x$ 本身的大,它就是后继,否则的话,在 $x$ 的右子树里找到最小值(进入右子树以后一直往左走即可)。
删除
删除操作保证 $x$ 存在于树内,那么一个 find 先给它 splay 到根,然后分类讨论:
-
cnt > 1,那么cnt -= 1即可返回。 -
否则,删除这个节点,然后根据它是否存在左右儿子来考虑。
2.1. 没有左右儿子:直接删除节点即可。
2.2. 有一个儿子:让这个儿子当根,然后删除节点即可。
2.3. 有两个儿子:让左儿子当根,将右儿子设为新根的右儿子,然后删除节点。
例题
例1 洛谷P3369 【模板】普通平衡树
题意
写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入一个数字 $x$。
- 删除一个数字 $x$(若有多个相同的数,应只删除一个)。
- 查询数字 $x$ 的排名。
- 查询排名为 $k$ 的数。
- 求 $x$ 的前驱。
- 求 $x$ 的后继。
题解
见模版。
例2 洛谷P3391【模板】文艺平衡树
题意
给定一个长度为 $n$ 的序列 $1, 2, …, n$,再给定 $m$ 次操作,每次操作指定一个区间 $[L,R]$,翻转这个区间。
输出所有操作结束后的结果。
其中,$n,m \leq 10^5$。
题解
与普通平衡树不一样的是,这次按照 index 作为权值。
那么我们翻转 $[L,R]$ 的时候,可以将 L-1 splay到根,然后让 R+1 成为其 right child,然后 R+1 的左儿子就变成了 $[L,R]$ 这个区间。
然后怎么翻转呢?给这个区间的根节点打上标记即可。标记下传时,将这个节点的左右儿子换一下。(注意和线段树不同的是,是先打标记,下传时才更换左右儿子)。
• 本质上相当于将这个子树的所有节点的左右儿子都翻转了。
为什么这样做是对的?
注意到一个区间的值的排序方式,对应的其实是平衡树的 in-order。如下图,对应的就是 $[1,2,3,4,5,6]$。
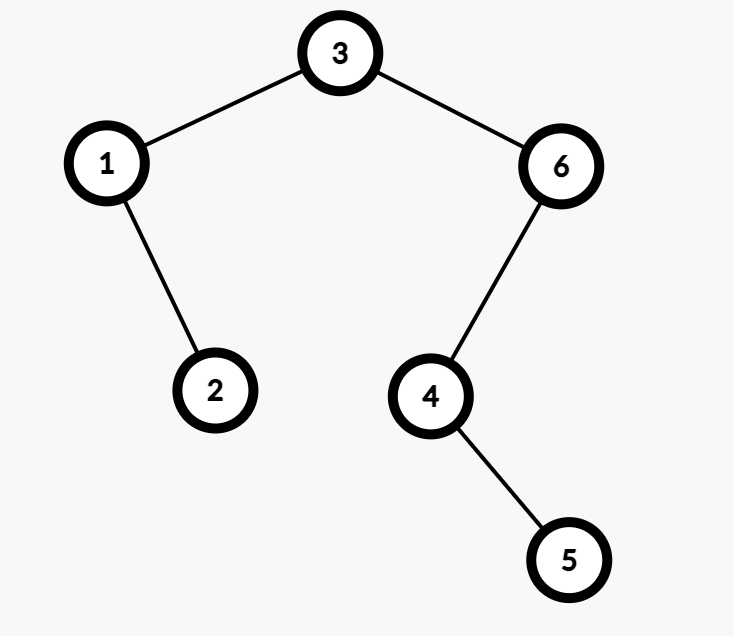
在翻转了所有节点的左右儿子以后如下图,可以发现现在的 in-order 就是 $[6,5,4,3,2,1]$ 了。
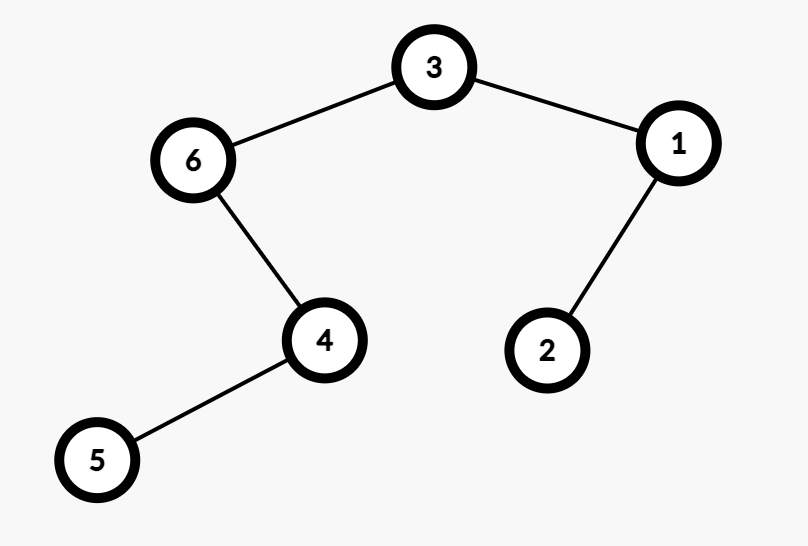
原因也很好理解,毕竟 in-order 就是根据左右子树的顺序来的。
但是,在换了左右儿子以后,看起来这个BST的结构被破坏了,不再是按照权值排序了?确实,但本来我们就不是按照权值排序的,图上的标号只不过是节点里储存的值,实际上,现在储存了 $6$ 的节点才是所谓的节点 $1$(意味着它在 kth(1) 时会被返回)。
这意味着:整棵平衡树已经不再使用 BST 的性质了,而是仅仅维护了一个 in-order 的结构而已。
那么我们要找到位于 $L-1$ 和 $R+1$ 的节点怎么办?用 kth() 函数即可。
• 注意到 kth() 函数是唯一一个没有用到 BST 性质的函数。
在最后,输出平衡树的 in-order 即可。
• 同时因为我们前面证明过,无论怎么旋转,这个树的 in-order 不变,所以改变 in-order 的也只有翻转左右儿子这个操作。
在实现的时候,如果要翻转整个区间 $1,n$,那么它们没有对应的 $L-1$ 和 $R+1$,我们就在一开始额外在首尾各加一个节点即可,分别赋值为 -1e9, 1e9。
题外话:如果这个时候我想按照数组的值本身来查询怎么办?比如我想知道哪个节点储存了 $3$ 这个值?
可以发现:无论怎么翻转左右儿子或者旋转,储存了 $3$ 这个值的节点 index 从来没变过,我们其实可以预先处理每个值所在的节点编号,到时候直接去里面找就行。
当然,这样只支持查询原本在数组里的值,至于前驱后继就没法查询了,它们必须使用 BST 的性质。
代码
#include <bits/stdc++.h>
using namespace std;
struct Splay {
struct Node {
int par, child[2], sz, cnt;
ll val, flag;
} tr[maxn];
int rt, id = 0;
void push_up(int cur) {
if (!cur) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
tr[cur].sz = tr[lc].sz + tr[rc].sz + tr[cur].cnt;
}
void push_down(int cur) {
if (!cur || !tr[cur].flag) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
swap(tr[cur].child[0], tr[cur].child[1]);
tr[lc].flag ^= 1, tr[rc].flag ^= 1;
tr[cur].flag = 0;
}
void clear(int cur) {
tr[cur].par = tr[cur].val = tr[cur].sz = tr[cur].cnt = tr[cur].child[0] = tr[cur].child[1] = 0;
}
bool isright(int cur) {
return cur == tr[tr[cur].par].child[1];
}
void rotate(int x) {
if (!x || x == rt) return;
int y = tr[x].par, z = tr[y].par;
push_down(y); push_down(x); // 注意先 push_down parent
bool r = isright(x); // 注意这里, 是先 push_down 之后,才判断 isright(x) 的
tr[y].child[r] = tr[x].child[r^1];
if (tr[x].child[r^1]) tr[tr[x].child[r^1]].par = y;
tr[x].child[r^1] = y;
tr[y].par = x;
tr[x].par = z;
if (z) tr[z].child[y == tr[z].child[1]] = x;
push_up(y); push_up(x);
}
void splay(int x, int tar = 0) {
assert(x != 0);
while (tr[x].par != tar) {
int y = tr[x].par, z = tr[y].par;
if (z != tar) {
if (isright(y) == isright(z)) rotate(y);
else rotate(x);
}
rotate(x);
}
if (tar == 0) rt = x;
}
void insert(ll val) {
if (!rt) {
tr[++id].val = val;
tr[id].cnt++;
rt = id;
push_up(id);
return;
}
int cur = rt, p = 0;
while (1) {
push_down(cur);
if (tr[cur].val == val) {
tr[cur].cnt++;
push_up(cur);
push_up(p);
splay(cur);
break;
}
p = cur;
cur = tr[p].child[tr[p].val < val];
if (!cur) {
cur = ++id;
tr[cur].val = val;
tr[cur].cnt++;
tr[cur].par = p;
tr[p].child[tr[p].val < val] = cur;
push_up(cur);
push_up(p);
splay(cur);
break;
}
}
}
int query_rank(int x) { // 查询 x 所在的rank
splay(find(x));
return tr[tr[rt].child[0]].sz + 1;
}
int kth(int k) { // 查询第k大 (注意返回的是节点编号,不是值)
int cur = rt;
assert(cur != 0);
while (1) {
push_down(cur); // pushdown
int lc = tr[cur].child[0], rc = tr[cur].child[1];
if (lc && k <= tr[lc].sz) {
cur = lc;
} else {
k -= (tr[cur].cnt + tr[lc].sz);
if (k <= 0) {
return cur;
}
cur = rc;
}
}
}
int find(ll x) {
// 找一个值为 x 的节点,如果找不到就寻找最近的一个(可大可小)
int cur = rt;
while (tr[cur].child[tr[cur].val < x] && tr[cur].val != x) {
push_down(cur);
cur = tr[cur].child[tr[cur].val < x];
}
return cur;
}
int pre() {
int cur = tr[rt].child[0];
if (!cur) return cur;
while (tr[cur].child[1]) cur = tr[cur].child[1];
splay(cur);
return cur;
}
int nxt() {
int cur = tr[rt].child[1];
if (!cur) return cur;
while (tr[cur].child[0]) cur = tr[cur].child[0];
splay(cur);
return cur;
}
void del(ll val) {
splay(find(val)); // 将它旋转到根
if (tr[rt].cnt > 1) {
tr[rt].cnt--;
push_up(rt);
return;
}
int lc = tr[rt].child[0], rc = tr[rt].child[1];
if (!lc && !rc) {
clear(rt);
rt = 0;
return;
}
if (!lc || !rc) {
int tmp = rt;
if (!lc) rt = rc;
else rt = lc;
tr[rt].par = 0;
clear(tmp);
return;
}
int tmp = rt, cur = pre(), splay(cur); // 现在 cur 变为根了
tr[tr[tmp].child[1]].par = cur;
tr[cur].child[1] = tr[tmp].child[1];
clear(tmp);
push_up(rt);
}
int find_pre(ll val) { // 查询前驱所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val < val) return rt;
else return pre();
}
int find_nxt(ll val) { // 查询后继所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val > val) return rt;
else return nxt();
}
void dfs(int cur) {
push_down(cur);
if (tr[cur].child[0]) dfs(tr[cur].child[0]);
if (tr[cur].val >= -1e8 && tr[cur].val <= 1e8)
cout << tr[cur].val << " ";
if (tr[cur].child[1]) dfs(tr[cur].child[1]);
}
} tr;
int main() {
int n, m; cin >> n >> m;
tr.insert(-1e9);
for (int i = 1; i <= n; i++) tr.insert(i);
tr.insert(1e9);
while (m--) {
int L, R; cin >> L >> R;
L++, R++;
int l = tr.kth(L-1); tr.splay(l);
int r = tr.kth(R+1); tr.splay(r, l);
assert(tr.rt == l);
tr.tr[tr.tr[r].child[0]].flag ^= 1;
}
tr.dfs(tr.rt);
cout << "\n";
}
例3 洛谷P3165[CQOI2014] 排序机械臂
题意
给定 $n$ 个正整数 $a_1,a_2,…,a_n$,然后进行 $n$ 次操作将这个数组排序,操作如下:
第 $i$ 次操作时,选择第 $i$ 大的数所在的位置 $p$,然后将 $[i,p]$ 这个区间翻转。
• 如果两个数相同,则按照它们在原数组的出现次序来决定相对次序。
输出每次操作时,选中的第 $i$ 大的数所在的位置。
其中,$n \leq 10^5, a_i \in [1, 10^7]$。
题解
区间翻转,和上题一样。不过这题需要选择当前第 $i$ 大的数。
不过记得上面我们提到,当一棵splay树被建好以后,无论怎么转,一个元素在哪个节点,它以后就不会动了。
所以我们预先sort所有的数,然后记录第 $i$ 大的数所在的节点编号即可。
这样每次询问的时候,一个 splay() 将第 $i$ 大的数 splay 到根节点,然后看一下它左子树有多大,就知道它所在的位置了。
• 不过注意,在翻转的时候,查询 L-1 和 R+1 还是得用 tr.kth() 函数,保证标记正确下传了,而不能直接用预先记录好的节点编号。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
struct Splay {
struct Node {
int par, child[2], val, sz, cnt;
int flag;
} tr[maxn];
int rt, id = 0;
void push_up(int cur) {
if (!cur) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
tr[cur].sz = tr[lc].sz + tr[rc].sz + tr[cur].cnt;
}
void push_down(int cur) {
if (!cur || !tr[cur].flag) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
swap(tr[cur].child[0], tr[cur].child[1]);
tr[lc].flag ^= 1, tr[rc].flag ^= 1;
tr[cur].flag = 0;
}
void clear(int cur) {
tr[cur].par = tr[cur].val = tr[cur].sz = tr[cur].cnt = tr[cur].child[0] = tr[cur].child[1] = 0;
}
bool isright(int cur) {
return cur == tr[tr[cur].par].child[1];
}
void rotate(int x) {
if (!x || x == rt) return;
int y = tr[x].par, z = tr[y].par;
push_down(y); push_down(x); // 注意先 push_down parent
bool r = isright(x); // 注意这里, 是先 push_down 之后,才判断 isright(x) 的
tr[y].child[r] = tr[x].child[r^1];
if (tr[x].child[r^1]) tr[tr[x].child[r^1]].par = y;
tr[x].child[r^1] = y;
tr[y].par = x;
tr[x].par = z;
if (z) tr[z].child[y == tr[z].child[1]] = x;
push_up(y); push_up(x);
}
void splay(int x, int tar = 0) {
while (tr[x].par != tar) {
int y = tr[x].par, z = tr[y].par;
if (z != tar) {
if (isright(y) == isright(z)) rotate(y);
else rotate(x);
}
rotate(x);
}
if (tar == 0) rt = x;
}
void insert(int val) {
if (!rt) {
tr[++id].val = val;
tr[id].cnt++;
rt = id;
push_up(id);
return;
}
int cur = rt, p = 0;
while (1) {
if (tr[cur].val == val) {
tr[cur].cnt++;
push_up(cur);
push_up(p);
splay(cur);
break;
}
p = cur;
cur = tr[p].child[tr[p].val < val];
if (!cur) {
cur = ++id;
tr[cur].val = val;
tr[cur].cnt++;
tr[cur].par = p;
tr[p].child[tr[p].val < val] = cur;
push_up(cur);
push_up(p);
splay(cur);
break;
}
}
}
int query_rank(int x) { // 查询 x 所在的rank
splay(find(x));
return tr[tr[rt].child[0]].sz + 1;
}
int kth(int k) { // 查询第k大 (注意返回的是节点编号,不是值)
int cur = rt;
while (1) {
push_down(cur); // pushdown
int lc = tr[cur].child[0], rc = tr[cur].child[1];
if (lc && k <= tr[lc].sz) {
cur = lc;
} else {
k -= (tr[cur].cnt + tr[lc].sz);
if (k <= 0) {
return cur;
}
cur = rc;
}
}
}
int find(int x) {
// 找一个值为 x 的节点,如果找不到就寻找最近的一个(可大可小)
int cur = rt;
while (tr[cur].child[tr[cur].val < x] && tr[cur].val != x) {
push_down(cur);
cur = tr[cur].child[tr[cur].val < x];
}
return cur;
}
int pre() {
int cur = tr[rt].child[0];
if (!cur) return cur;
while (tr[cur].child[1]) cur = tr[cur].child[1];
splay(cur);
return cur;
}
int nxt() {
int cur = tr[rt].child[1];
if (!cur) return cur;
while (tr[cur].child[0]) cur = tr[cur].child[0];
splay(cur);
return cur;
}
void del(int val) {
splay(find(val)); // 将它旋转到根
if (tr[rt].cnt > 1) {
tr[rt].cnt--;
push_up(rt);
return;
}
int lc = tr[rt].child[0], rc = tr[rt].child[1];
if (!lc && !rc) {
clear(rt);
rt = 0;
return;
}
if (!lc || !rc) {
int tmp = rt;
if (!lc) rt = rc;
else rt = lc;
tr[rt].par = 0;
clear(tmp);
return;
}
int tmp = rt, cur = pre(), splay(cur); // 现在 cur 变为根了
tr[tr[tmp].child[1]].par = cur;
tr[cur].child[1] = tr[tmp].child[1];
clear(tmp);
push_up(rt);
}
// 查询 val 的前驱的值
int query_pre(int val) {
splay(find(val));
if (tr[rt].val < val) return tr[rt].val;
else return tr[pre()].val;
}
int query_nxt(int val) {
splay(find(val));
if (tr[rt].val > val) return tr[rt].val;
else return tr[nxt()].val;
}
} tr;
int cnt[(int)(1e7+5)], pos[maxn];
struct Data {
int val, cnt, id;
} a[maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].val;
cnt[a[i].val]++;
a[i].cnt = cnt[a[i].val];
a[i].id = i;
}
sort(a+1, a+n+1, [](auto a, auto b) {
return tuple {a.val, a.cnt} < tuple {b.val, b.cnt};
});
for (int i = 1; i <= n; i++) {
pos[i] = a[i].id + 1;
}
tr.insert(-1e9);
for (int i = 1; i <= n; i++) {
tr.insert(i);
}
tr.insert(1e9);
for (int i = 1; i <= n; i++) {
int p = pos[i];
tr.splay(p);
int rt = tr.rt;
int sz = tr.tr[tr.tr[rt].child[0]].sz;
cout << sz << " ";
int L = tr.kth(i); tr.splay(L);
int R = tr.kth(sz+2); tr.splay(R, L);
tr.tr[tr.tr[R].child[0]].flag ^= 1;
}
cout << "\n";
}
例4 BZOJ4923 K小值查询
题意
维护一个长度为 $n$ 的正整数序列 $a_1,a_2,…,a_n$,现在有 $m$ 次操作,支持以下两种操作:
$1~ k$:输出当前序列第 $k$ 大的值。
$2~ k$:将所有 $>k$ 的数 $a_i$ 减去 $k$。
其中,$n,m \leq 10^5, a_i \in [1,10^9]$。
题解
splay的区间操作不仅限于反转(用index作为权值),同样也可以对某一个值域区间内的数进行操作(前提是不破坏splay本身的结构)。
然而这个题,将所有 $>k$ 的数 $a_i$ 减去 $k$ 似乎会破坏splay本身的结构?
于是分类讨论:
对于在 $[k+1, 2k]$ 的数,可以将它们删掉,然后减去 $k$ 以后再塞回去。
对于 $>2k$ 的数,则利用打标记的方式,因为将它们减去 $k$ 并不影响 splay 的整体结构。
那么修改的时候,就查询一下 $k+1$ 的前驱 $x$ splay 到根,然后查询一下 $2k$ 的后继 $y$ splay到以 $x$ 为根,和上一题一样的处理方法,那么 $y$ 的左儿子就是 $[k+1,2k]$ 的数了。删除的时候其实不需要一个个删,只需要直接把这个子树的根和splay断开就行了。
• 由于有额外insert,注意多开一倍空间,同时注意到可能有重复的值,所以要根据 cnt 来进行insert。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
vector<int> vec;
int n;
struct Splay {
struct Node {
int par, child[2], sz, cnt;
ll val, flag;
} tr[maxn];
int rt, id = 0;
void push_up(int cur) {
if (!cur) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
tr[cur].sz = tr[lc].sz + tr[rc].sz + tr[cur].cnt;
}
void push_down(int cur) {
if (!cur || !tr[cur].flag) return;
int lc = tr[cur].child[0], rc = tr[cur].child[1];
ll f = tr[cur].flag;
tr[lc].flag += f, tr[rc].flag += f;
tr[lc].val += f, tr[rc].val += f;
tr[cur].flag = 0;
}
void clear(int cur) {
tr[cur].par = tr[cur].val = tr[cur].sz = tr[cur].cnt = tr[cur].child[0] = tr[cur].child[1] = 0;
}
bool isright(int cur) {
return cur == tr[tr[cur].par].child[1];
}
void rotate(int x) {
if (!x || x == rt) return;
int y = tr[x].par, z = tr[y].par;
push_down(y); push_down(x); // 注意先 push_down parent
bool r = isright(x); // 注意这里, 是先 push_down 之后,才判断 isright(x) 的
tr[y].child[r] = tr[x].child[r^1];
if (tr[x].child[r^1]) tr[tr[x].child[r^1]].par = y;
tr[x].child[r^1] = y;
tr[y].par = x;
tr[x].par = z;
if (z) tr[z].child[y == tr[z].child[1]] = x;
push_up(y); push_up(x);
}
void splay(int x, int tar = 0) {
assert(x != 0);
while (tr[x].par != tar) {
int y = tr[x].par, z = tr[y].par;
if (z != tar) {
if (isright(y) == isright(z)) rotate(y);
else rotate(x);
}
rotate(x);
}
if (tar == 0) rt = x;
}
void insert(ll val) {
if (!rt) {
tr[++id].val = val;
tr[id].cnt++;
rt = id;
push_up(id);
return;
}
int cur = rt, p = 0;
while (1) {
push_down(cur);
if (tr[cur].val == val) {
tr[cur].cnt++;
push_up(cur);
push_up(p);
splay(cur);
break;
}
p = cur;
cur = tr[p].child[tr[p].val < val];
if (!cur) {
cur = ++id;
tr[cur].val = val;
tr[cur].cnt++;
tr[cur].par = p;
tr[p].child[tr[p].val < val] = cur;
push_up(cur);
push_up(p);
splay(cur);
break;
}
}
}
int query_rank(int x) { // 查询 x 所在的rank
splay(find(x));
return tr[tr[rt].child[0]].sz + 1;
}
int kth(int k) { // 查询第k大 (注意返回的是节点编号,不是值)
int cur = rt;
assert(cur != 0);
while (1) {
push_down(cur); // pushdown
int lc = tr[cur].child[0], rc = tr[cur].child[1];
if (lc && k <= tr[lc].sz) {
cur = lc;
} else {
k -= (tr[cur].cnt + tr[lc].sz);
if (k <= 0) {
return cur;
}
cur = rc;
}
}
}
int find(ll x) {
// 找一个值为 x 的节点,如果找不到就寻找最近的一个(可大可小)
int cur = rt;
while (tr[cur].child[tr[cur].val < x] && tr[cur].val != x) {
push_down(cur);
cur = tr[cur].child[tr[cur].val < x];
}
return cur;
}
int pre() {
int cur = tr[rt].child[0];
if (!cur) return cur;
while (tr[cur].child[1]) cur = tr[cur].child[1];
splay(cur);
return cur;
}
int nxt() {
int cur = tr[rt].child[1];
if (!cur) return cur;
while (tr[cur].child[0]) cur = tr[cur].child[0];
splay(cur);
return cur;
}
void del(ll val) {
splay(find(val)); // 将它旋转到根
if (tr[rt].cnt > 1) {
tr[rt].cnt--;
push_up(rt);
return;
}
int lc = tr[rt].child[0], rc = tr[rt].child[1];
if (!lc && !rc) {
clear(rt);
rt = 0;
return;
}
if (!lc || !rc) {
int tmp = rt;
if (!lc) rt = rc;
else rt = lc;
tr[rt].par = 0;
clear(tmp);
return;
}
int tmp = rt, cur = pre(), splay(cur); // 现在 cur 变为根了
tr[tr[tmp].child[1]].par = cur;
tr[cur].child[1] = tr[tmp].child[1];
clear(tmp);
push_up(rt);
}
int find_pre(ll val) { // 查询前驱所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val < val) return rt;
else return pre();
}
int find_nxt(ll val) { // 查询后继所在的编号,需要保证一定存在
splay(find(val));
if (tr[rt].val > val) return rt;
else return nxt();
}
void dfs(int cur, int k) {
if (!cur) return;
push_down(cur);
if (tr[cur].val >= k+1 && tr[cur].val <= 2*k) {
vec.push_back(cur);
}
dfs(tr[cur].child[0], k);
dfs(tr[cur].child[1], k);
}
} tr;
int main() {
int n, m; cin >> n >> m;
tr.insert(-1e18);
for (int i = 1; i <= n; i++) {
int a; cin >> a;
tr.insert(a);
}
tr.insert(1e18);
while (m--) {
int op, k; cin >> op >> k;
if (op == 1) {
cout << tr.tr[tr.kth(k+1)].val << "\n";
} else {
vec.clear();
int rt = tr.find_pre(k+1); // < k+1
int x = tr.find_nxt(2*k); // > 2*k
tr.splay(rt);
tr.splay(x, rt);
int lc = tr.tr[x].child[0];
int rc = tr.tr[x].child[1];
tr.dfs(lc, k);
if (lc) {
assert(tr.tr[lc].par == x);
tr.tr[lc].par = 0;
tr.tr[x].child[0] = 0;
}
assert(x != 0);
tr.tr[x].flag -= k;
tr.tr[x].val -= k;
sort(vec.begin(), vec.end());
vec.resize(unique(vec.begin(), vec.end()) - vec.begin());
vector<int> tmp;
for (int j : vec) {
if (tr.tr[j].val >= k+1)
for (int k = 0; k < tr.tr[j].cnt; k++) tmp.push_back(j);
}
vec = tmp;
for (int nd : vec) {
ll v = tr.tr[nd].val;
tr.insert(v - k);
}
}
}
}
注意事项
- 做这种题的时候,不要吝啬
push_down(),能加的地方尽量多加加。 - 由于前驱和后继不一定存在,而splay不支持在其不存在的情况下进行操作,那么我们在一开始手动加上前驱 $-10^{18}$ 和后继 $10^{18}$。
- 在修改时,先查找好需要splay的节点,然后再一起 splay,因为查找的过程中可能会调用
pre()和nxt()导致根被改变了。
