强连通分量（SCC）

定义

在一个 有向图 中，任意取两个节点 $(u,v)$，$u \rightarrow v, v \rightarrow u$ 均有路径，这样的图叫做强连通。

SCC（强连通分量）：一个极大的强连通子图。

缩点：当我们求出一个图中的所有 SCC 后，我们可以将每一个 SCC 缩成一个点。缩点过后，我们可以得到一个新的图，我们遍历所有 原图中的边，将原图中的边加到新图中（注意判断自环，并且一般会出现重复边）。

• 缩点后得到的图一定是一个 DAG（有向无环图）。

• DAG 有着很多优秀的性质，比如可以进行 拓扑排序，可以利用拓扑排序进行 DP 等。

求一个有向图中的强连通分量，有两种算法，Tarjan 与 kosaraju 算法（复杂度均为 $O(n+m)$）。

Tarjan 求有向图的 SCC

算法流程

定义 $DFS$ 树为：从任意节点出发，形成的一条从上往下的生成树。

当我们从 $u$ 访问到 direct neighbor $v$ 时，如果 $v$ 尚未被访问过，那么 $(u,v)$ 是一条树边。否则 $(u,v)$ 是一条 非树边。

我们先维护一个栈 st[]，里面储存的是我们当前正在处理的 SCC。

定义两个数组 $dfn[u], low[u]$。

$dfn[u]$ ：DFS过程中，节点 $u$ 的编号（前序编号）。
$low[u]$ ：当前，在栈中的所有节点，以下两者的最小值：
1. $u$ 的子树中，所有节点 $v$ 的 $low[v]$ 最小值。
2. 从 $u$ 出发，经过一条 非树边 达到节点 $v$ 的 $dfn[v]$ 的最小值。

void dfs(int u) {
    // ....
    in[u] = 1;  // u 进栈
    st[++tail] = u;  // 进栈
    dfn[u] = low[u] = ++id;  // 前序编号
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);  // 需要在栈内
        if (!dfn[to]) {
            dfs(to);
            low[u] = min(low[u], low[to]);
        }
    }
    // ....

经过 DFS 后，我们可以发现，在栈内，有且仅有一个节点 $u$ 使得 $dfn[u] = low[u]$。这个节点就代表 SCC 在DFS树中的根节点。

所以，当我们进行DFS回溯的时候，检查一下当前节点 $u$ 是否满足 $dfn[u] = low[u]$。如果满足，将栈中所有的节点（直到 $u$ 为止）全部拿出来，就是一个新的 SCC 了。

// from[u] 代表 u 所在的SCC编号，scc代表scc编号，sz[scc] 代表对应scc的大小
int n, m;
vector<int> adj[maxn];

struct Tarjan {
    int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn];
    bool in[maxn];  // instack or not
    int st[maxn], tail = -1;
    void dfs(int u) {
        in[u] = 1;
        st[++tail] = u;
        dfn[u] = low[u] = ++id;
        for (int to : adj[u]) {
            if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);  // 要记得在栈内
            if (!dfn[to]) {
                dfs(to);
                low[u] = min(low[u], low[to]);
            }
        }
        if (dfn[u] == low[u]) {
            from[u] = ++scc;
            sz[scc] = 1;
            while (tail >= 0 && st[tail] != u) {
                int cur = st[tail];
                from[cur] = from[u];
                sz[scc]++;
                tail--;
                in[cur] = 0;  // 记得这里，将在栈中的标记去掉
            }
            tail--;
            in[u] = 0;  // 记得这里，将在栈中的标记去掉
        }
    }
    // 跑tarjan
    void solve() {
        for (int i = 1; i <= n; i++) {
            if (!dfn[i]) dfs(i);
        }
    }
} tj;

例题洛谷P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

题意

给定一个 $N$ 个节点，$M$ 条边的有向图。

定义一个节点 $u$ 为明星，当且仅当：

对于 任意节点 $v$ ，均有至少一条到 $u$ 的路径。

问，图中有多少个节点是明星？

题解

对原图跑一次tarjan求SCC，然后缩点。

缩点后，我们会发现 新图中只有一个明星。

• 如果新图中有 $2$ 个明星，那么明星 $1$ 存在到明星 $2$ 的边，反之亦然。那么明星 $1,2$ 就属于同一个SCC，contradiction。

并且我们会发现，明星的 out-degree 一定为 $0$，否则，明星指向的节点也是一个明星。

所以，如果缩点后，新图满足：存在且仅存在 $1$ 个节点，使得它的 out-degree 为 $0$，那么有解，输出这个SCC对应的大小即可。

代码

const int maxn = 1e4+5;
const int maxm = 5e4+10;

struct Edge {
    int to, nxt;
} edges[maxm];
int head[maxn], ecnt = 1, n,m;

void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}

int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn];
bool in[maxn];  // instack or not
int st[maxn], tail = -1;
void dfs(int u) {
    in[u] = 1;
    st[++tail] = u;
    dfn[u] = low[u] = ++id;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);
        if (!dfn[to]) {
            dfs(to);
            low[u] = min(low[u], low[to]);
        }
    }

    if (dfn[u] == low[u]) {
        from[u] = ++scc;
        sz[scc] = 1;
        while (tail >= 0 && st[tail] != u) {
            int cur = st[tail];
            from[cur] = from[u];
            sz[scc]++;
            tail--;
            in[cur] = 0;
        }
        tail--;
        in[u] = 0;
    }
}

int deg[maxn];
void build() {
    for (int u = 1; u <= n; u++) {
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].to;
            int fu = from[u], fv = from[v];
            if (fv == fu) continue;  // 记得去掉自环
            deg[fu]++;
        }
    }
}

void tarjan() {
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) dfs(i);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        addEdge(u,v);
    }
    tarjan();
    build();
    int cnt = 0, ans;
    for (int i = 1; i <= scc; i++) {
        if (!deg[i]) cnt++, ans = i;
    }
    if (cnt > 1) cout << 0 << endl;
    else cout << sz[ans] << endl;
}

kosaraju 算法

kosaraju 算法本质上利用了 正反 $2$ 次DFS 求出一个图中的强连通分量。

算法流程

建立原图 $G$，和一个反图 $G'$（将所有的边反过来）
在原图 $G$ 上跑 DFS，回溯的时候记录 ID。
在反图 $G'$ 上跑 DFS，起始节点的顺序是 ID从大到小。每次 DFS 的 起始节点 就代表了一个新的SCC，DFS访问到的所有节点就是这个SCC。

感性理解

如果将原图进行一个缩点操作，那么我们可以得到一个DAG：

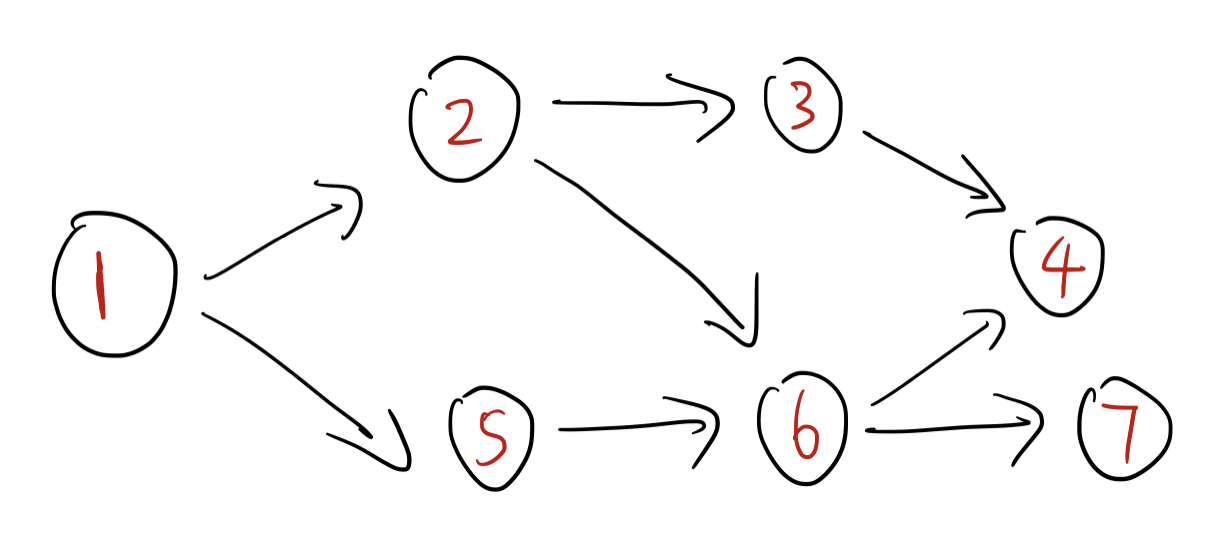
如上图，可以看出节点 $1$ 拥有 支配地位（它能到达别的点，但是别的点无法到达它）。

也可以说，节点 $1$ 在拓扑序中，位置最靠前。

由于我们是回溯的时候才记录 ID，所以节点 $1$ 的 ID 是最大的。

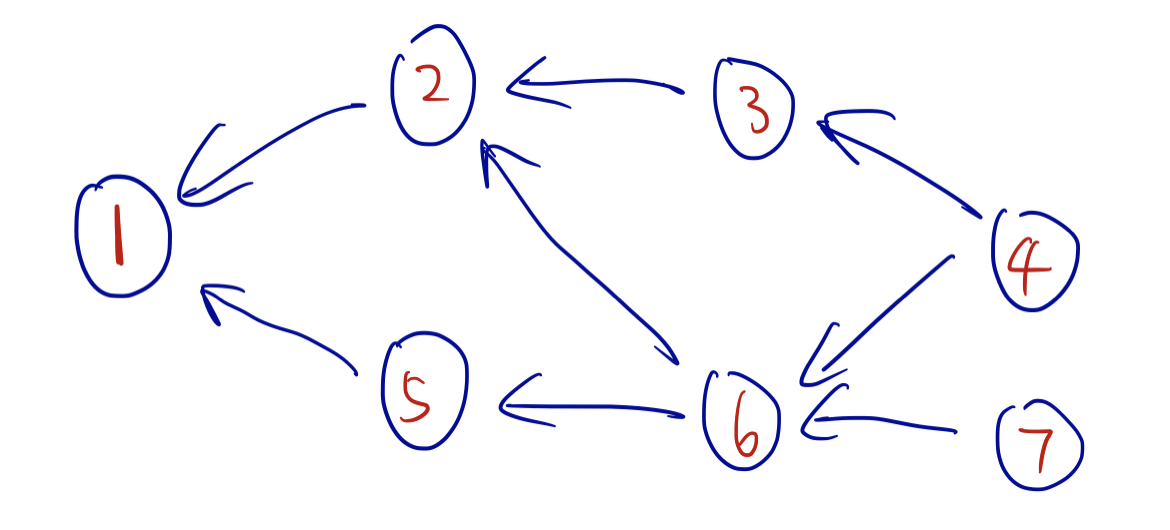
那么，在反图 $G'$ 中，所有节点的地位反转了，节点 $1$ 的地位最低，且它在拓扑序中，位置最靠后。

为了找到 SCC，我们希望的就是找到一个节点，使得它无法到达任何其他节点。那么节点 $1$ 就是我们想要的。

这解释了为什么我们要 ID从大到小 进行反图的 DFS。

注：原图不一定连通，DFS的时候要注意。

模版题

洛谷P2863 [USACO06JAN]The Cow Prom S

题意

给定 $n$ 个节点，$m$ 条边的有向图。

求点数大于 $1$ 的SCC个数。

代码

const int maxn = 1e4+5;
const int maxm = 5e4+5;

struct Edge {
    int to, nxt;
} edges[maxm], redges[maxm];
int head[maxn], rhead[maxn], ecnt = 1, recnt = 1;

void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

void rev_addEdge(int u, int v) {
    Edge e = {v, rhead[u]};
    rhead[u] = recnt;
    redges[recnt++] = e;
}

int id[maxn], idcnt = 0;
bool vis[maxn];
void dfs(int u) {
    vis[u] = 1;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (vis[to]) continue;  // 已经访问过了，忽略
        dfs(to);
    }
    id[++idcnt] = u;  // 回溯的时候更新ID
}

int sz[maxn];
void dfs2(int u) {
    sz[u] = 1;
    for (int e = rhead[u]; e; e = redges[e].nxt) {
        int to = redges[e].to;
        if (sz[to]) continue;  // 已经访问过，忽略
        dfs2(to);
        sz[u] += sz[to];
    }
}

int main() {
    int n,m; cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        addEdge(u,v); 
        rev_addEdge(v,u);
    }

    for (int i = 1; i <= n; i++) {
        if (!vis[i]) dfs(i);
    }
 
    int ans = 0;
    for (int i = n; i >= 1; i--) {
        if (!sz[id[i]]) {  // 还没dfs过，说明这是一个新的SCC
            dfs2(id[i]);
            if (sz[id[i]] > 1) 
                ans++;
        }
    }
    cout << ans << endl;
}

例题

例1 洛谷P3119 [USACO15JAN]Grass Cownoisseur G

题意

给定一个 $n$ 个节点，$m$ 条边的有向图。

现在我们需要从 $1$ 号节点出发，走一条路径，再返回到 $1$ 号节点。（每个节点可以被通过多次）。

我们允许反向穿过一条边，但是只能反向一次。

输出我们能够访问的 distinct 节点的最大数量。

其中，$1 \leq n,m \leq 10^5$

题解

看到 每个节点可以被穿过多次，首先想到缩点。

缩点后，假设我们去掉 可以反向一次 的这个条件，那么答案就是 $1$ 所属的SCC的大小。

因为我们只能反向一次，我们可以想到利用 分层图 的思想。

我们先缩点，得到一个新图 $G_1$，然后将缩点后的图 复制一份，得到 $G_2$。

对于 $G_1$ 中的每条边 $(u_1,v_1)$，我们建一条新边 $(v_1, u_2)$，从 $G_1 \rightarrow G_2$。

观察到我们只能由 $G_1 \rightarrow G_2$，又因为 $G_1 = G_2$ 且 $G_1,G_2$ 均为 DAG，所以整个图中满足以下条件：

无环（仍然是一个DAG）
$G_1 \rightarrow G_2$ 只能发生一次。（从 $G_2$ 无法返回 $G_1$）

所以问题就转化为：

在这个新图中，从 $G_1$ 的 $s_1$（$1$ 所属的SCC）出发，到 $G_2$ 的 $s_1$，最多能经过多少个节点？

将 $G_1,G_2$（包括$G_1 \rightarrow G_2$）中，所有边 $(u,v)$ 赋上权值 $size[v]$。那么我们只要求

从 $G_1$ 的 $s_1$（$1$ 所属的SCC）出发，到 $G_2$ 的 $s_1$ 的最长路 即可。

• 注：最长路不能用 dijkstra，只能用 SPFA。复杂度最坏 $O(nm)$

• 注2：对于 DAG 而言，求最长路也可以直接用 拓扑排序 + DP。复杂度 $O(n+m)$，在DAG中，可以完美替代 SPFA

• 注3：需要特判一下原图是不是一个SCC（一般这种题都要特判一下）。如果是，直接输出答案 $n$。

正确性证明：我们为什么不需要考虑 重复经过某个节点，然后多算了的情况？

答：因为我们不可能重复经过某个节点。

证：如果我们在 $G_1$ 中经过了某个节点 $u$，说明 $1$ 是可以到达 $u$ 的。

那么，如果在 $G_2$ 中经过了同样的节点 $u$，然后由 $u$ 又返回了 $1$。这说明 $1 \rightarrow u \rightarrow 1$ 是一个环。然而缩点后的图不可能有环，contradiction。

代码（SPFA）

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;

struct Edge {
    int to,nxt;
} edges[maxn];
int head[maxn], ecnt = 1, id = 0, scc = 0, from[maxn], sz[maxn], st[maxn], tail = -1, n, m, dfn[maxn], low[maxn];
bool in[maxn];

void addEdge(int u, int v) {
    Edge e = {v, head[u]};
    edges[ecnt] = e;
    head[u] = ecnt++;
}

void dfs(int u) {
    dfn[u] = low[u] = ++id;
    in[u] = 1;
    st[++tail] = u;
    for (int e = head[u]; e; e = edges[e].nxt) {
        int to = edges[e].to;
        if (dfn[to] && in[to]) {
            low[u] = min(low[u], dfn[to]);
        }
        if (!dfn[to]) {
            dfs(to);
            low[u] = min(low[u], low[to]);
        }
    }

    if (dfn[u] == low[u]) {
        from[u] = ++scc;
        sz[scc] = 1;
        while (st[tail] != u) {
            int cur = st[tail--];
            from[cur] = from[u];
            sz[scc]++;
            in[cur] = 0;
        }
        tail--;
        in[u] = 0;
    }
}


void tarjan() {
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) dfs(i);
    }
}

struct New_Edge {
    int to, nxt, w;
} new_edges[maxn<<2];
int new_head[maxn<<1], new_ecnt = 1;

void new_addEdge(int u, int v, int w) {
    New_Edge e = {v, new_head[u], w};
    new_head[u] = new_ecnt;
    new_edges[new_ecnt++] = e;
}

void build() {
    for (int u = 1; u <= n; u++) {
        for (int e = head[u]; e; e = edges[e].nxt) {
            int v = edges[e].to;
            int fu = from[u], fv = from[v];
            if (fu == fv) continue;   // 注意判重
            new_addEdge(fu, fv, sz[fv]);   // 原边
            new_addEdge(fu+scc, fv+scc, sz[fv]);  // 复制
            new_addEdge(fv, fu+scc, sz[fu]);  // 反向边
        }
    }
}

int d[maxn<<1];  // 因为复制了一份，记得开2倍大小
bool inq[maxn<<1];
queue<int> q;
void spfa() {
    q.push(from[1]);
    inq[from[1]] = 1;  // 注意是 from[1]
    while (!q.empty()) {
        int cur = q.front(); q.pop();
        inq[cur] = 0;
        for (int e = new_head[cur]; e; e = new_edges[e].nxt) {
            int to = new_edges[e].to, w = new_edges[e].w;
            if (d[cur] + w > d[to]) {  // 无论是否 inq[] 都要更新
                d[to] = d[cur] + w;
                if (!inq[to])
                    q.push(to);
                inq[to] = 1;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        addEdge(u,v);
    }
    tarjan();
    build();
    spfa();

    int ans = d[from[1] + scc];  // 注意是 from[1]
    if (scc == 1) ans = n;  // 需要特判一下整个图是否为强连通分量
    cout << ans << endl;
}

代码（拓扑排序 + DP）

因为其他部分完全一样，这里就省略，只保留 main() 和 DP 部分。


void solve() {
    tail = -1;
    fill(dp, dp+2*scc+1, -1e9);  // 注意赋值为 -inf，因为我们只关心从 from[1] 出发的部分
    dp[from[1]] = 0;

    for (int u = 1; u <= 2*scc; u++) {
        if (!ind[u]) st[++tail] = u;
    }
    while (tail >= 0) {
        int cur = st[tail--];
        for (int e = new_head[cur]; e; e = new_edges[e].nxt) {
            int to = new_edges[e].to, w = new_edges[e].w;
            dp[to] = max(dp[to], dp[cur] + w);
            ind[to]--;
            if (!ind[to]) st[++tail] = to;
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u,v; cin >> u >> v;
        addEdge(u,v);
    }
    tarjan();
    build();
    solve();

    int ans = dp[from[1] + scc];  // 注意是 from[1]
    if (scc == 1) ans = n;  // 需要特判一下整个图是否为强连通分量
    cout << ans << endl;
}

Contents

定义

Tarjan 求有向图的 SCC

算法流程

例题 洛谷P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

kosaraju 算法

算法流程

感性理解

模版题

例题

例1 洛谷P3119 [USACO15JAN]Grass Cownoisseur G

例题洛谷P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G