线性基
Contents
介绍
线性基是一般用于解决 子集XOR,XOR最值 一类问题的算法。
定义
线性基是一个 linear space,在这个space中,所有的向量为 非负整数,而 scalar 则为 $\{0,1\}$,元素之间的运算为 XOR。
可以直接与 linear algebra 中,由矩阵组成的 linear space 直接关联起来,并且专属名词的定义与矩阵 linear space 中的基本相同。
性质
-
线性基 $S = \{x_1,x_2,…,x_n\}$ 中,所有元素 $\{x_1,x_2,…,x_n\}$ 之间是 linearly independent 的。
-
线性基 $S = \{x_1,x_2,…,x_n\}$ 中的所有元素组成了一个 basis,意味着 $$\forall x \in span(S), x = a_1x_1 + a_2x_2 + … a_nx_n$$ 且 $(a_1,a_2,…,a_n)$ 是 unique 的。($a_i \in \{0,1\}$)
-
在线性基中,每个元素的二进制最高位均不同。
-
对于线性基第 $i$ 位上的元素
a[i],保证a[i]二进制第 $i$ 位为 $1$,并且:$\forall j > i$,
a[i]的二进制第 $j$ 位为 $0$。对于 $j < i$,
a[i]的二进制第 $j$ 位可以为 $1$ 或者 $0$。
推论
根据线性基的性质,有以下推论:
-
从 $S$ 中取任意个(至少 $1$ 个)元素,它们的 XOR 均不为 $0$。
-
$S$ 中任意元素 $x_i$ 均 无法 由其他元素 XOR 得到。
-
对于一个非负整数 $x$,如果在 $S$ 中,取一些元素 $x_{a_1}, x_{a_2}, …, x_{a_k}$ 使得 $x = XOR(\{x_{a_1}, x_{a_2}, …, x_{a_k}\})$,则:
使用 $x$ 替换掉 $x_{a_1}, x_{a_2}, …, x_{a_k}$ 中的任意一个,线性基均不变。
如何找到这样的 $x_1, x_2, …, x_k$ 使得 $x = XOR(\{x_{a_1}, x_{a_2}, …, x_{a_k}\})$?
答:在正常的
insert()过程中,如果执行了x ^= a[j],就说明 $x_j \in \{x_{a_1}, x_{a_2}, …, x_{a_k}\}$。注:为了维持线性基的特性,不能直接进行替换。
正确方式是在正常的
insert()过程中,在遇到想要替换的j时,进行swap(x, a[j]),然后再x ^= a[j]。
构造方法
构造线性基是一个 动态过程,意味着我们逐一往线性基中 插入元素 来构造。
我们利用一个数组 ll a[63] 来维护线性基。
其中 a[i] 代表线性基中的一个元素,它的二进制最高位为第 $i$ 位(从右往左数)。如果 a[i] = 0,说明这个元素不存在。
insert 操作
当我们向线性基中插入一个元素 $x$ 时,遵循以下步骤:
-
从高位往低位,遍历 $x$ 的二进制bit。
-
遍历到第 $i$ 位时,如果 $x$ 的第 $i$ 位为 $0$,直接跳到下一位。
如果 $x$ 的第 $i$ 位为 $1$,则:
2.1. 如果
a[i] = 0(说明这一位不存在元素),则令a[i] = x,然后break。(说明插入元素成功)。2.2. 如果
a[i] > 0(说明这一位存在元素),则令x = x ^ a[i],然后继续遍历下一位bit。
ll a[63];
bool insert(ll x) {
for (int j = 62; j >= 0; j--) {
if (x & (1LL<<j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x; // 插入元素 x
return 1; // 插入元素成功
}
}
}
return 0; // 插入元素失败
}
由以上的过程,可以看出:
插入元素 $x$ 成功 $\iff x \notin span(S)$,插入后 $span(S)$ 的大小翻倍。
插入元素 $x$ 失败 $\iff x \in span(S)$。
query 操作
查询一个元素 $x$ 是否满足 $x \in span(S)$,只要遵循上面的 insert 操作,然后不进行真正的插入即可。
应用
最大子集 XOR 和
Q: 给定一个数组 $S$,求它的子集 $S’ \subseteq S$,使得 $S'$ 中所有元素的 XOR值 最大。
A: 构造 $S$ 的线性基,然后从高到低位遍历线性基,如果 ans ^ a[i] 更大,则 ans = ans ^ a[i]。
例 洛谷P3812 【模板】线性基
题意
给定 $n$ 个整数(数字可能重复),求在这些数中选取任意个,使得他们的异或和最大。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
ll a[62];
void insert(ll x) {
for (int j = 60; j >= 0; j--) {
if (x & (1LL<<j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
break;
}
}
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
ll x; cin >> x;
insert(x);
}
ll ans = 0;
for (int j = 60; j >= 0; j--) {
ans = max(ans, (ans ^ a[j]));
}
cout << ans << endl;
}
例题
例1 洛谷P3857 [TJOI2008]彩灯
题意
有 $n$ 个彩灯,$m$ 个开关,每个开关会控制一些彩灯的状态。每个彩灯只有开和关两种状态。初始状态下所有彩灯为关。
求所有可能的彩灯样式数量。
其中,$n,m \leq 50$
题解
每个开关看成一个数字,然后构建原集合的线性基。
最终答案为 $2^{|S|}$,其中 $|S|$ 为线性基的大小。
证明:因为线性基中,对于每个二进制位,如果有,则仅有一个元素 $x$ 使得 $x$ 的最高位为 $1$。
先令集合 $X = \{0\}$,代表 $span(S)$。
我们从低位开始往高位考虑,对于第 $i$ 位而言,如果 a[i] 存在,则将 $X$ 内所有的元素与 a[i] 进行 XOR,会得到最高位 $i$ 为 $1$ 的元素,而原来 $X$ 中并不存在这样的元素,所以 $X$ 的大小翻倍了。
注意,在使用 bit shifting 的时候,要注意用
1LL << j,而不是1 << j,后者会爆 int。
代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
ll a[62];
void insert(ll x) {
for (int j = 60; j >= 0; j--) {
if (x & (1LL<<j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
break;
}
}
}
}
int main() {
cin >> n >> m;
if (!m) {
cout << 0 << endl; return 0;
}
for (int i = 1; i <= m; i++) {
string s; cin >> s;
ll x = 0;
for (int j = 0; j < n; j++) {
if (s[n-j-1] == 'O') {
x |= (1LL<<j);
}
}
insert(x);
}
ll ans = 1, cnt = 0;
for (int j = 60; j >= 0; j--) {
if (a[j]) cnt++;
}
ans = (1LL<<cnt) % 2008LL;
cout << ans << endl;
}
例2 洛谷P4570 [BJWC2011]元素
题意
有 $n$ 个矿石,每个矿石 $i$ 拥有一个元素序号 $a_i$,还有一个魔力值 $b_i$。
请选出一些矿石,使得这些矿石的元素序号的 XOR 不为 $0$,并且使得魔力值之和最大。
题解
先根据魔力值从大到小 sort 一下所有矿石,然后根据这个顺序,加入矿石的元素序号到线性基中。
最终把线性基中,所有矿石对应的魔力值加起来即可。
代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
ll a[63];
bool insert(ll x) {
for (int j = 62; j >= 0; j--) {
if (x & (1LL<<j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
return 1;
}
}
}
return 0;
}
struct node {
ll x, val;
} arr[maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> arr[i].x >> arr[i].val;
}
sort(arr+1, arr+n+1, [](auto a, auto b) {
return a.val > b.val;
});
ll ans = 0;
for (int i = 1; i <= n; i++) {
if (insert(arr[i].x)) {
ans += arr[i].val;
}
}
cout << ans << endl;
}
例3 洛谷P3292 [SCOI2016]幸运数字
题意
给定一个 $n$ 个节点的树,每个节点 $i$ 都有一个权值 $a_i$。
现在给定 $q$ 个询问,每次询问 $x ~ y$,回答:
对于从 $x$ 到 $y$ 的最短路径上的所有节点,选出一个子集使得权值的 XOR 最大,回答这个最大值。
其中,$n \leq 2 \times 10^4, q \leq 10^5$,所有权值为非负整数。
题解
首先暴力做法很好想,直接找 $x \rightarrow y$ 路径上的所有权值,构建一个线性基即可。
然后考虑优化:
看到 树 就立刻想到 树形DP,看到 树形DP 就立刻想到了 树上差分。
虽然这题不能直接用树上差分,但是差分中常用的 倍增LCA 倒是可以用。
所以做法就是对于每个节点 $u$,令 $j = 0,1,2,…$,代表从 $u$ 出发,往上跳 $2^j$ 个节点,从起点到终点之间所有节点的权值构建的线性基。
所以构建出的数组就是个 ll a[maxn][16][61]; // a[u][k] 代表从 u 开始往上从 2^k 格,形成的线性基。
构建这个线性基的过程和倍增同理,只不过需要 两个线性基合并为一个。
这个过程也不难,直接把两个线性基中的所有元素拿出来,然后都 insert 进一个空的线性基即可。
最后,询问 $x ~ y$ 的话就先找到 $l = lca(x,y)$,然后通过倍增,合并出 $(x,l)$ 和 $(y,l)$ 对应的线性基,然后再将两者合并即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e4+5;
const int maxm = 1e5+5;
int n,q;
ll arr[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int par[maxn][16], dep[maxn];
ll a[maxn][16][61]; // a[u][k] 代表从 u 开始往上从 2^k 格,形成的线性基
// insert 一个元素 x 进入 b[] 中
void insert(ll x, ll b[]) {
for (int j = 60; j >= 0; j--) {
if (x & (1LL<<j)) {
if (b[j]) x ^= b[j];
else {
b[j] = x;
return;
}
}
}
}
// 将 a1, a2 两个线性基合并为 b
void merge(ll a1[], ll a2[], ll b[]) {
for (int j = 60; j >= 0; j--) {
if (a1[j]) insert(a1[j], b);
if (a2[j]) insert(a2[j], b);
}
}
void dfs(int u, int p) {
par[u][0] = p;
insert(arr[u], a[u][0]);
dep[u] = dep[p] + 1;
for (int j = 1; j <= 15; j++) {
par[u][j] = par[par[u][j-1]][j-1];
merge(a[u][j-1], a[par[u][j-1]][j-1], a[u][j]);
}
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p) continue;
dfs(to, u);
}
}
int jump(int u, ll d, ll b[]) {
int j = 0;
while (d) {
if (d & 1) {
for (int k = 60; k >= 0; k--) {
if (a[u][j][k]) insert(a[u][j][k], b);
}
u = par[u][j];
}
j++;
d >>= 1;
}
return u;
}
ll query(int u, int v) {
if (dep[u] < dep[v]) swap(u,v);
static ll tmp[61];
memset(tmp, 0, sizeof(tmp));
u = jump(u, dep[u] - dep[v], tmp);
if (u == v) {
insert(arr[u], tmp);
} else {
for (int j = 15; j >= 0; j--) {
if (par[u][j] != par[v][j]) {
u = jump(u, (1LL<<j), tmp);
v = jump(v, (1LL<<j), tmp);
}
}
u = jump(u, 1, tmp);
v = jump(v, 1, tmp);
insert(arr[u], tmp);
insert(arr[v], tmp);
}
ll ans = 0;
for (int j = 60; j >= 0; j--) {
if (tmp[j]) ans = max(ans, (ans ^ tmp[j]));
}
return ans;
}
int main() {
fastio;
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> arr[i];
for (int i = 1; i <= n-1; i++) {
int u,v; cin >> u >> v;
addEdge(u,v); addEdge(v,u);
}
dfs(1, 0);
while (q--) {
int u,v; cin >> u >> v;
cout << query(u,v) << "\n";
}
}
例4 洛谷P4151 [WC2011]最大XOR和路径
题意
给定 $n$ 个节点,$m$ 条边的无向连通图。每条边上有权值。
考虑从 $1$ 到 $n$ 的所有可能路径中,路径上所有边权值的XOR,求这些路径对应的XOR最大值。
路径可以包含环,一条边可以被经过多次(经过多次的话,权值也要XOR多次)。
图中可能包含重边和自环。
其中,$n \leq 5 \times 10^4, m \leq 10^5$
题解
首先考虑一下 无环 的情况,那它就是个树了,那路径只有一种可能。就是从 $1 \rightarrow n$。
然后考虑一下 有环 的情况,
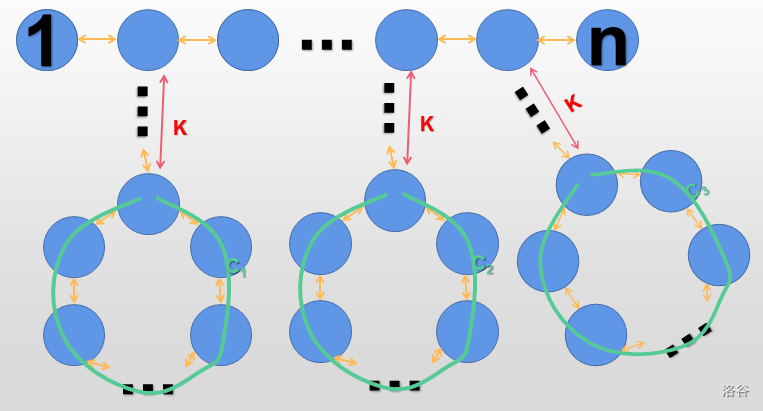
可以发现,最终的答案可以是 $1 \rightarrow n$ 的路径(我们称之为 主路径),XOR上这些环(也可以不 XOR),而链接环与主路径之间的边,可以忽略不计(因为被经过两次了)。
所以一个大胆(且正确)的猜想是:
求出所有的环,随便找一条 $1 \rightarrow n$ 的简单路径(无环),用所有环的XOR值构造一个线性基,最后和主路径XOR起来,得到最大值。
然后就有几个问题了:
Q1. 求出所有的环?复杂度会爆炸的吧?
A1. 我们可以发现,所有环的 XOR 均由它的 简单环 组成。所以我们只需要考虑简单环即可。
Q2. 如何求出所有的简单环?
A2. 用一次DFS,DFS的过程中找到所有的 back-edge 即可,由于 $m$ 最多为 $10^5$,所以 back-edge 也不会超过 $10^5$ 个,所以最多只有 $10^5$ 个简单环。
Q3. 主路径如果有多条怎么办?
A3. 注意到,尽管只往线性基里加入了简单环,但是由于线性基的特性,所以任意简单环的组合都可以被线性基所表示。所以这就相当于线性基包含了所有可能的环。
那么,如果从 $1 \rightarrow n$ 有多条简单路径,则两条不同的简单路径会形成一个环。
假如最优的主路径为 $B$,而我们考虑了 $A$ 为主路径,但是 $A ~xor~ B$ 实际上是一个环。所以最后我们在考虑最终答案时,有 $A \text{ xor } (A \text{ xor } B) = B$,所以 $B$ 就变成最优解中的主路径了。
Q4. 如何求出一个环的 XOR?
A4. 直接从 $1$ 开始DFS,记录一个 d[],其中 d[u] 代表这个 DFS 过程中,找到的一条 $1 \rightarrow u$ 的简单路径的 XOR。
则对于 $u$ 的任意一个neighbor $v$,如果 $(u,v,w)$ 是 back-edge,那么 $(d[u] \text{ xor } d[v] \text{ xor } w)$ 就是这个环的 XOR。
最后的答案就是 d[n] 作为初始值,所有简单环构建出线性基,然后求最大值。
• 注意到 d[n] 并不在线性基中,因为 d[n] 是 必须要取 的,所以作为 ans 的初始值。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4+5;
const int maxm = 1e5+5;
int n,m;
struct Edge {
int to, nxt;
ll w;
} edges[maxm<<1];
int head[maxn], ecnt = 1;
void addEdge(int u, int v, ll w) {
Edge e = {v, head[u], w};
edges[ecnt] = e;
head[u] = ecnt++;
}
ll d[maxn], a[62];
void insert(ll x) {
for (int j = 60; j >= 0; j--) {
if (x & (1LL << j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
return;
}
}
}
}
bool vis[maxn];
void dfs(int u) {
vis[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
ll w = edges[e].w;
if (vis[to]) { // 发现 back-edge,对应一个简单环
insert(d[u] ^ d[to] ^ w); // 加入一个简单环
} else {
d[to] = d[u] ^ w;
dfs(to);
}
}
}
int main() {
fastio;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u,v; ll w;
cin >> u >> v >> w;
addEdge(u,v,w);
addEdge(v,u,w);
}
dfs(1);
ll ans = d[n]; // 注意 d[n] 作为初始值,因为它必须要存在于最终答案中
for (int j = 60; j >= 0; j--) {
ans = max(ans, (ans ^ a[j]));
}
cout << ans << endl;
}
例5 LOJ 114 k小异或和
题意
给定 $n$ 个非负整数,$m$ 次询问。
每次询问一个数字 $k$,输出 $S$ 所有非空子集的不同的XOR中,第 $k$ 小的XOR值。
如果 $S$ 的所有非空子集中,不同的XOR数量 $< k$,则输出 $-1$。
其中,$n,m \leq 10^5$。
题解
本题主要考察 线性基的化简。
首先可以构建线性基,如果在构建中出现了 插入失败 的情况,则说明 $\exists T \subseteq S$,使得 $XOR(T) = 0$,这说明最小值为 $0$,否则最小值不为 $0$。
构建完毕后,我们知道,$span(S)$ 的大小为 $2^{|S|}$。
我们设 $span(S_i)$ 为:只考虑(从小到大)前 $i$ 位的线性基的 $span$,则有:
$span(S_i) = span(S_{i-1}) \sqcup span(S_{i-1}) \text{ xor } x_i$ (注意 $\sqcup$ 是 disjoint union)
由此,我们可以联想到,把 $k$ 写成二进制,然后根据 $k$ 的二进制,来构造这个数字。
比如,$k = 1101$,那么我们就把线性基的第 $0,2,3$ 位 XOR 起来,得到答案。
但是这样有一个问题,这样得到的答案不一定正确。比如说:
线性基 $\{1,2\}$ 和 $\{1,3\}$ 实际上是等价的,但是对于同样的 $k$,答案却不相同,只有 $\{1,2\}$ 构造出来的答案才是正确的。
所以我们有了一个想法:把线性基上 每一位的数字转化为它可能的最小值,也就是 化简线性基。
这个化简的过程,很像高斯消元,但又不完全一样。
怎么化简呢?
想到我们求一个线性基所能表示的最大值时,使用的 ans = max(ans, (ans ^ a[i]))。
那么化简也是同理,只不过把它改成 min 而已,然后把 ans 替换为线性基上的某一位即可。
// 将线性基所有元素变成最小
for (int k = 50; k >= 0; k--) {
for (int j = k-1; j >= 0; j--) {
a[k] = min(a[k], (a[k] ^ a[j]));
}
}
这样就化简完毕了,举几个例子:
- $\{70,32,28,8,4,3,1\}$ 化简后,得到 $\{64,32,16,8,4,2,1\}$
- $\{14, 7\}$ 化简后,得到 $\{9,7\}$
化简后就可以用上面的方法来构造了,注意构造答案的时候,只需要考虑线性基上非空的位。
代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
ll a[51];
bool insert(ll x) {
for (int j = 50; j >= 0; j--) {
if (x & (1LL << j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
return 1;
}
}
}
return 0;
}
int main() {
cin >> n;
bool zero = 0;
for (int i = 1; i <= n; i++) {
ll x; cin >> x;
if (!insert(x)) zero = 1;
}
int sz = 0;
for (int k = 50; k >= 0; k--) {
if (a[k]) sz++;
}
// 将线性基所有元素变成最小
for (int k = 50; k >= 0; k--) {
for (int j = k-1; j >= 0; j--) {
a[k] = min(a[k], (a[k] ^ a[j]));
}
}
// 只考虑线性基的非空位
vector<int> vec;
for (int k = 0; k <= 50; k++) {
if (a[k]) vec.push_back(k);
}
cin >> m;
while (m--) {
ll k; cin >> k;
if (zero) k--; // 最小值为 0
if (k >= (1LL << sz)) {
cout << -1 << "\n";
continue;
}
ll ans = 0;
for (int j = 0; j <= 50; j++) {
if (k & (1LL << j)) {
ans ^= (a[vec[j]]); // 只考虑非空位
}
}
cout << ans << "\n";
}
}
例6 HDU6579 Operation
题意
给定 $n$ 个非负整数 $a_1,a_2,…,a_n$ 和 $m$ 个询问。
每次询问为两种:
$0 ~ l ~ r$:从 $\{a_l,…,a_r\}$ 中选取任意个数字,输出 XOR 的最大值。
$1 ~ x$:给序列 append 一个数字 $x$,使得 $n = n+1$。
所有询问强制在线。
其中,$n,m \leq 5 \times 10^5$。
题解
前缀线性基。
对于每个 $i$,我们都根据 $\{a_1,a_2,…,a_i\}$ 来构建一个线性基,所以总共有 $n$ 个线性基。
构建以后,每次询问 $[L,R]$,我们都可以先找到 $[1,R]$ 对应的线性基。
找到 $[1,R]$ 的线性基以后,问题转化成,如何去掉 $[1,L-1]$ 的影响?
我们维护一个数组 pos[],其中 pos[j] 代表 最大 的index i,使得 $a_i$ 影响到了 线性基的第 $j$ 位 $x_j$。
所以,在询问 $[L,R]$ 时,我们遍历 $[1,R]$ 对应的线性基中,每一位 $j \in [0,50]$,如果 $pos[j] \geq L$,则说明线性基的第 $j$ 位可以被使用。
如何维护 pos[] 数组,并且保证 pos[] 数组内的值尽可能大?
在线性基的推论第 $3$ 条中,我们提到了如果要使用一个新的元素来替换掉线性基中的旧元素,可以使用 swap() 的方式实现。
这里也是同理,我们在 insert $a_i$ 时,如果当前考虑到了线性基的第 $j$ 位,那么我们检查 $pos[j] < i$ 是否成立,如果是,就进行替换操作(swap())。
• 如果这个题可以离线,就可以预处理一下所有的询问,按照 右端点排序,在从左往右扫的时候维护一个 pos[31] 数组即可。
离线版本可以见:ABC223H
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5; // 注意因为 n 最高可被增加到 1e6,所以这里使用的是 1e6
const int maxm = 1e5+5;
int n,m;
int a[maxn][31], pos[maxn][31]; // 其中 pos[j] 代表 最大 的index i,使得 $a_i$ 影响到了 线性基的第 $j$ 位 $x_j$。
void insert(int i, int x) {
memcpy(a[i], a[i-1], 31 * sizeof(int)); // 注意这里有 sizeof(int)
memcpy(pos[i], pos[i-1], 31 * sizeof(int));
int p = i;
for (int j = 30; j >= 0; j--) {
if (x & (1<<j)) {
if (a[p][j]) {
if (pos[p][j] < i) { // 进行替换
swap(a[p][j], x);
swap(pos[p][j], i);
}
x ^= a[p][j];
} else {
a[p][j] = x;
pos[p][j] = i;
return;
}
}
}
}
int query(int l, int r) {
int ans = 0;
for (int j = 30; j >= 0; j--) {
if (pos[r][j] >= l)
ans = max(ans, (ans ^ a[r][j]));
}
return ans;
}
int main() {
int T; cin >> T;
while (T--) {
int lastans = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int x; cin >> x;
insert(i, x);
}
while (m--) {
int op; cin >> op;
if (op == 0) {
int l,r; cin >> l >> r;
l = (l ^ lastans) % n + 1;
r = (r ^ lastans) % n + 1;
if (l > r) swap(l,r);
lastans = query(l,r);
cout << lastans << "\n";
} else {
int x; cin >> x;
x = x ^ lastans;
insert(n+1, x);
n++;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= 30; j++) {
a[i][j] = pos[i][j] = 0;
}
}
}
}
例7 ABC141F Xor Sum 3
题意
给定 $n$ 个非负整数,将它们分为两个非空集合 $A,B$,求 $XOR(A) + XOR(B)$ 的最大值?
其中,$2 \leq n \leq 10^5$
题解
分为两个集合的话,就可以考虑二进制每一位的count的奇偶性。
对于第 $i$ 位bit而言:
- 如果 count 是奇数:那么无论怎么分,最后分出来的两个集合一定是 奇 + 偶 的形式,所以最后一定会贡献 $2^i$ 给答案。
- 如果 count 是偶数:最后分出来,要么为 奇 + 奇,要么为 偶 + 偶,所以对于这些位置,分出来的两个数 $a,b$ 一定是相同的。
所以我们先把 奇数count 的位置贡献算出来,然后把它们全部置为 $0$,接下来所有的位就只有偶数 count 了,此时无论怎么分,最后得到的两个数字都是相同的,也就是答案等于 $2x$。
所以我们只要让 $x$ 最大就好了,用线性基解决即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
ll a[61], arr[maxn], ans = 0;
int n;
void insert(ll x) {
for (int j = 60; j >= 0; j--) {
if (x & (1LL << j)) {
if (a[j]) x ^= a[j];
else {
a[j] = x;
return;
}
}
}
}
int cnt[61];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
for (int j = 60; j >= 0; j--) {
if (arr[i] & (1LL << j)) cnt[j] ^= 1;
}
}
for (int j = 60; j >= 0; j--) {
if (cnt[j]) {
ans += (1LL << j);
for (int i = 1; i <= n; i++) {
if (arr[i] & (1LL << j)) arr[i] -= (1LL << j);
}
}
}
for (int i = 1; i <= n; i++) insert(arr[i]);
ll x = 0;
for (int j = 60; j >= 0; j--) {
x = max(x, (x^a[j]));
}
cout << 2LL*x + ans << endl;
}
