高斯消元
Contents
板子
代码
struct GaussianElimination {
int n, m; // n: 行 (方程个数), m: 列 (变量个数)
double A[1002][1002];
GaussianElimination(int n, int m) : n(n), m(m) {}
vector<double> solve(int B = (int)1e6) {
// B: band 大小,指对于任意 A(i,j) != 0,若 i2-i > B || j2-i > B 则任意 A(i2,j2) = 0;若 B = 1e6 则无此限制
// 返回 x_1, x_2, ..., x_m (注意返回的长度为 m+1),所以 x_1 = ans[1]
vector<double> ans(m+1, 0);
vector<int> var, free_var; // 主元,自由元
int row = 1;
for (int col = 1; col <= m; col++) {
int maxrow = row;
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (abs(A[i][col]) > abs(A[maxrow][col])) { // 在 mod 情况下找到一个非0即可
maxrow = i;
}
}
if (abs(A[maxrow][col]) < eps) {
// 自由元, 跳过这个 col,但row不变
free_var.push_back(col);
continue;
} else { // 主元
var.push_back(col);
}
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) swap(A[row][j], A[maxrow][j]);
swap(A[row][m+1], A[maxrow][m+1]);
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (i == row) continue;
double in = A[i][col] / A[row][col];
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) {
A[i][j] -= (in * A[row][j]);
}
A[i][m+1] -= (in * A[row][m+1]);
}
row++; // 增加 row
}
row--; // 因为row是从1开始的,所以会多加一次 (现在 [1,row] 代表了主元)
assert(row == var.size());
if (row < n) { // 要么无解,要么有无数多个解
for (int i = row + 1; i <= n; i++) {
if (abs(A[i][m+1]) > eps) return {}; // 无解
}
// 否则,有无数多个解,将自由元设为 0,输出主元的解
}
// 有解 和 无数个解 都输出了
for (int i = row; i >= 1; i--) {
// 此时,主元是 var[i-1]
int k = var[i-1];
for (int j = k+1; j <= min(m, k+2*B); j++) {
A[i][m+1] -= A[i][j] * ans[j];
A[i][j] = 0;
}
ans[k] = A[i][m+1] / A[i][k];
}
return ans;
}
};
介绍
高斯消元是矩阵操作里最基础的一个,主要用于解形如 $a_1x_1 + a_2x_2 + a_3x_3 = b_1$ 之类的线性方程组。
步骤
- 按 column 进行遍历
- 遍历到第 $k$ 个 column 时,在这个column中,寻找一个 $maxrow$ 使得 $A[maxrow][k]$ 最大(注意这个
maxrow > k),因为消元时,在 $k$ 行上面的所有行都被消成 unit vector 的形式了。 - 将第 $k$ 行 与 第 $maxrow$ 行进行交换。
- 交换后,以第 $k$ 行作为pivot,消去第 $k$ 列它下方所有行上的数字。
- 最后会得到一个 triangular matrix,左下方的所有值为 $0$,然后从右下方开始回代,即可得到 $\vec{b}$。
复杂度:$O(n^3)$
• 然而上述是针对 $n \times n$ 的矩阵,并且保证有唯一解时的做法。
无解或多解
假设我们给定 $n \times m$ 的矩阵,代表 $n$ 个方程和 $m$ 个变量。
我们用 row 和 col 来记录当前的行和列。
如果在第 $2$ 步,找不到 maxrow(即当前行下方的所有行 row 的 col 对应的值 A[row][col] 均为 $0$),则说明无唯一解。
这个时候,我们保证当前行不变,继续下一列。
那么最后 row 所在的位置就是 主元 的个数,而 $m-row$ 则为自由元的个数。
这样的话,相当于把所有自由元放在了最后几个全为 $0$ 的空行中。
例如遇到自由元 $x_3$ 时,跳过第 $3$ 列,保持 row 不变,那么第 $3$ 行保留的主元实际上是 $x_4$,而第 $4$ 行保留的主元是 $x_5$。
• 最后,在 [row+1, n] 之间的所有行必定为空行,我们只要看这一行的最右侧系数 $c$ 是否均为 $0$,如果均为 $0$ 就是无数个解,否则无解。
带状矩阵优化
在很多题目中(尤其是一些 dp 题),矩阵是带状的,
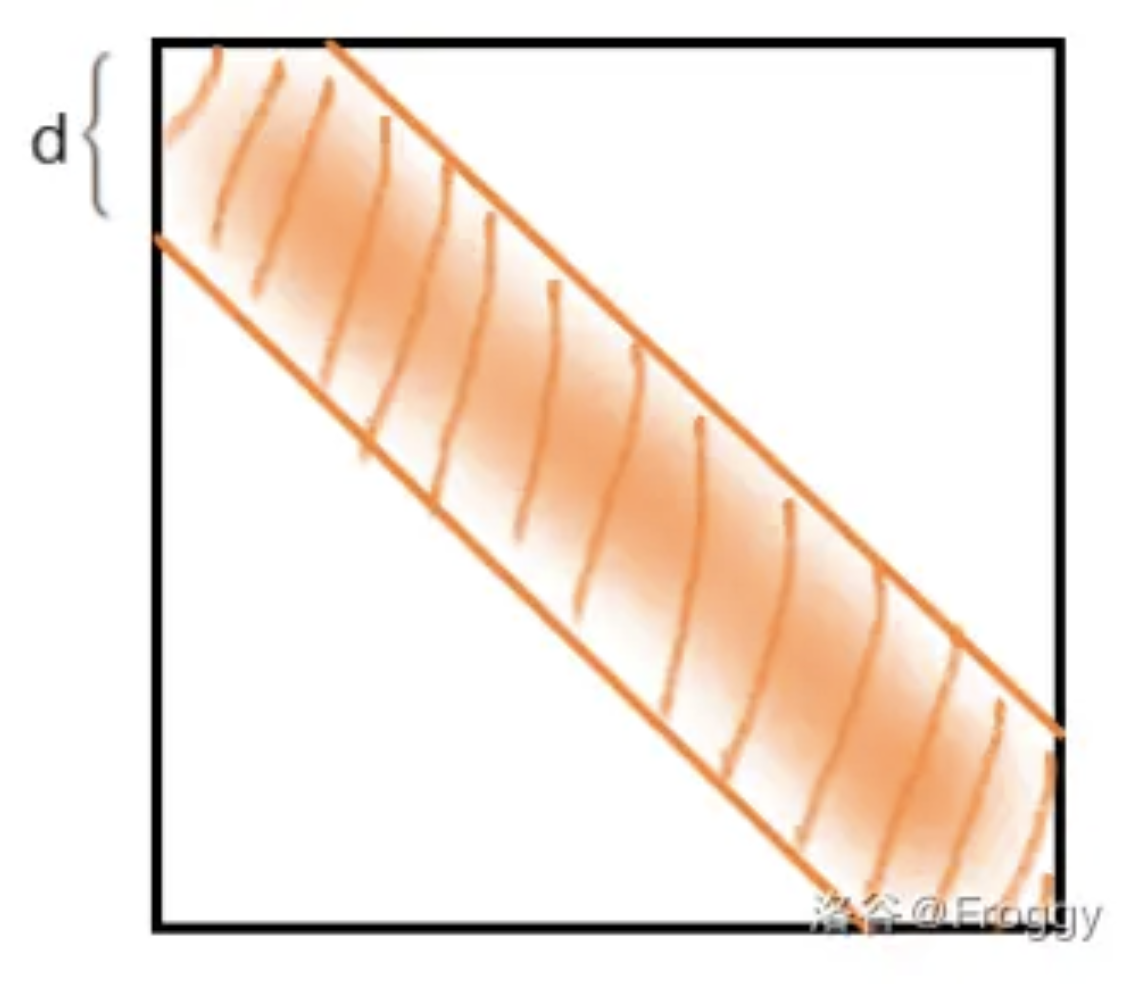
• 图上用 $d$ 表示了带状矩阵的宽,下文用 $B$ 来表示。
如图,仅有橙色部分非 $0$。更严谨的定义:
对于任何 $A_{i,j} \neq 0$,$\forall (i’,j’)$,若 $|i-i'| > B$,或者 $|j-j'| > B$,则 $A_{i’,j’} = 0$。
对于这样的矩阵,可以注意到在消元时,只需要往上和往下消 $B$ 行即可,同样,在减去一行/交换一行时,也最多只用往左和往右延伸 $B$ 格。
复杂度:$O(n B^2)$
带状矩阵的注意事项
- 在换行时,可能会导致带状矩阵的形状被破坏,不过由于换行只会考虑下方的 $B$ 行,将其换上来,所以最坏情况也就是带状矩阵的宽变成了 $2B$,所以实现的时候,需要考虑 $[i-2B, i+2B]$ 的行。
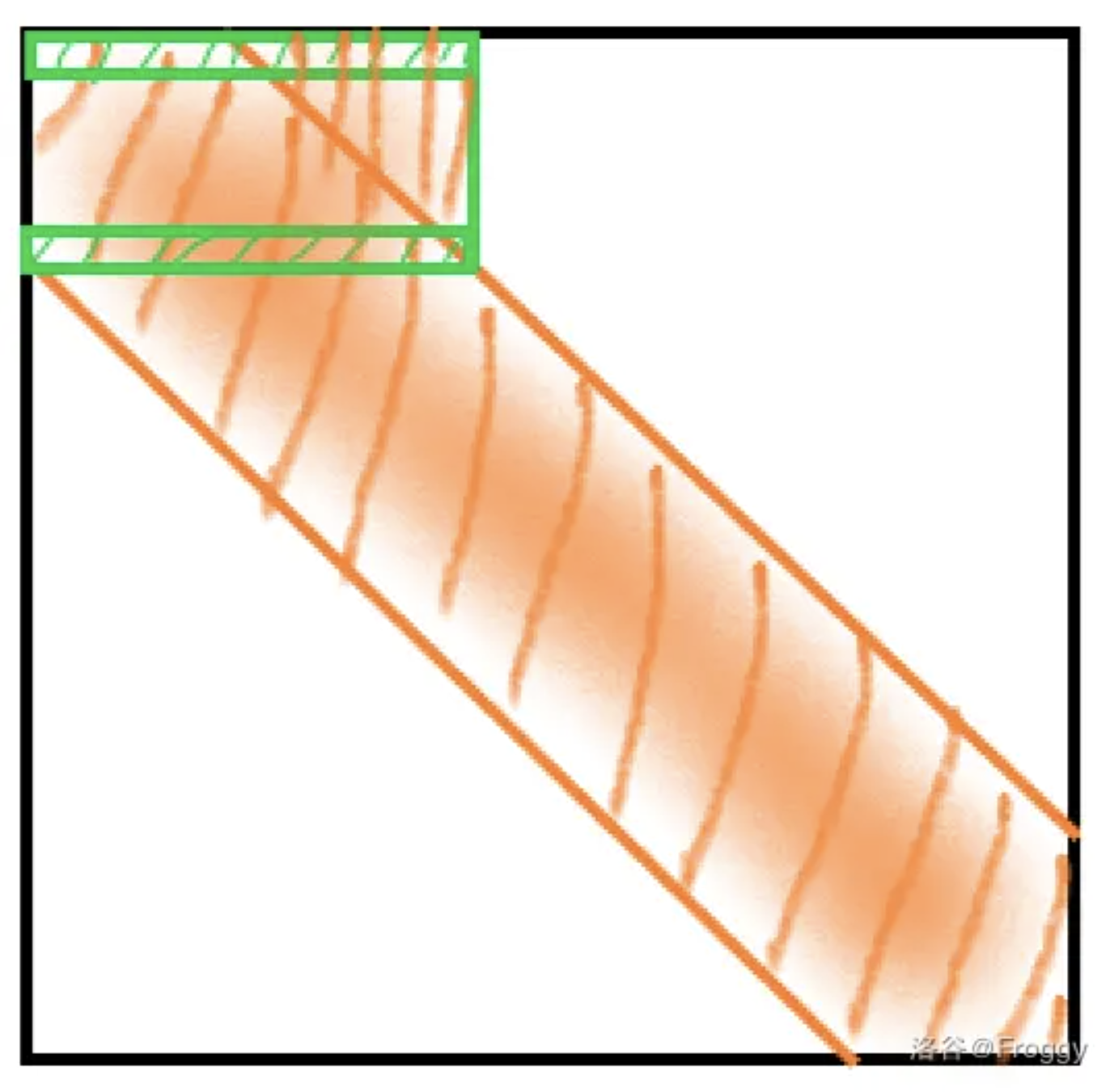
- 由于带状矩阵的性质,不能用高斯-约旦消元(即,消元时不能往上消,只能往下消),最后得到一个 triangular matrix 再回代才行。
01矩阵优化
在矩阵中的值只有 $0,1$ 的情况下,所有的值之间的加法和减法可以统一用 XOR 来表示,这样得到的就是一个异或方程组了。
所以可以将每一行表示为一个 bitset,然后行之间相减就直接用 bs[i] ^ bs[j] 即可。
这样的复杂度是 $O(\frac{n^3}{w})$ 的。
• 注意,在 bitset 中,一行是反过来排列的(index $0$ 从右边开始)。
代码见 例1
模版 P3389 【模板】高斯消元法
题意
给定一个线性方程组,进行求解。
输入一个 $n \times (n+1)$ 的矩阵,每一行为 $a_1, a_2, …, a_n, b_k$,代表一组方程。
#include <bits/stdc++.h>
using namespace std;
const double eps = (double)1e-6;
double A[maxn][maxn];
int n;
void solve() {
for (int k = 1; k <= n; k++) {
int maxrow = k; // 当前行初始情况下为:当前列对应的行数
for (int i = k+1; i <= n; i++) { // 从当前行往下找 (因为 i < k 的话,A[i][i] != 0 但其他位置 = 0)
if (abs(A[i][k]) > abs(A[maxrow][k])) maxrow = i;
}
for (int i = 1; i <= n+1; i++) swap(A[k][i], A[maxrow][i]); //交换两行, 保证A[k][k]最大
if (abs(A[k][k]) < eps) {
cout << "Infinite solutions." << endl; // 出现一行全是 0 的情况,一般说明有无数个解
return;
}
for (int i = 1; i <= n; i++) {
if (i == k) continue;
double m = A[i][k] / A[k][k];
for (int j = 1; j <= n+1; j++) { //更新上下的行
A[i][j] -= (m * A[k][j]);
}
}
}
for (int i = 1; i <= n; i++) {
A[i][n+1] /= A[i][i]; // 最后除以斜线上的系数
A[i][i] = 1.0;
printf("%.2f\n", A[i][n+1]);
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n+1; j++) {
cin >> A[i][j]; // 输入矩阵,j=n+1 代表 b
}
}
solve();
}
例题
例1 洛谷P2447[SDOI2010]外星千足虫
题意
有 $n$ 个虫子,每只虫子来自地球或者火星。来自地球的虫子有偶数个脚,火星的虫子有奇数个脚。
现在给定 $m$ 个方程,代表已知哪些虫子的脚数量之和为奇数或者偶数。
求每个虫子的归属地(地球或者火星)。
如果有解,输出最小的 $k \leq n$ 使得仅用前 $k$ 个方程即可得到结果。
如果无解,则输出 Cannot Determine。
其中,$1 \leq n \leq 10^3, 1 \leq m \leq 2 \times 10^3$。
题解
高斯消元即可。现在有几个问题:
Q1. 如果有解,如何求出 $k$?
A1. 注意到高斯消元的第二步是寻找一个 $maxrow$。然而这个题中,矩阵中的数要么为 $0$,要么为 $1$。所以只要找到 $1$,就不需要再往下找了。
所以在寻找 $1$ 的过程中记录一下用到的 row number 的最大值即可,一旦找到就立刻break。
Q2. 高斯消元是 $O(n^3)$ 的,复杂度不对?
A2. 再次注意到这个矩阵仅由 $0,1$ 组成,可以用 bitset 进行优化。优化幅度为 $\frac{1}{w}$,其中 $w=32$。
所以复杂度为 $O(\frac{n^2m}{w})$,足以通过本题。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3+2;
bitset<maxn> A[maxn+maxn];
int ans;
int n,m;
void solve() {
for (int k = 1; k <= n; k++) {
int maxrow = k;
for (int i = k; i <= m; i++) {
ans = max(ans, i);
if (A[i][n-k+1]) { // 注意 bitset 是反过来的
maxrow = i;
break;
}
}
swap(A[k], A[maxrow]);
if (!A[k][n-k+1]) { // 说明这一列全是 0
cout << "Cannot Determine\n";
return;
}
for (int i = 1; i <= m; i++) {
if (i == k) continue;
if (A[i][n-k+1])
A[i] ^= A[k];
}
}
cout << ans << endl;
for (int i = 1; i <= n; i++) {
if (A[i][0]) cout << "?y7M#\n"; // 注意bitset是反过来的,所以最右边代表解的那个值,实际上是 A[i][0]
else cout << "Earth\n";
}
}
int main() {
cin >> n >> m;
if (m < n) {
cout << "Cannot Determine\n";
return 0;
}
ans = 1;
for (int i = 1; i <= m; i++) {
string s1,s2; cin >> s1 >> s2; // input: 01110 1
A[i] = bitset<maxn>(s1 + s2); // 将解放在右边 (A[i][0])
}
solve();
}
例2 洛谷P4035 [JSOI2008]球形空间产生器
题意
在 $n$ 维空间中,有一个球体。现在已知该球面上 $(n+1)$ 个点的坐标,求出球心坐标?
其中,$1 \leq n \leq 10$,数据保证有唯一解。
题解
设球心坐标为 $(b_1,b_2,…,b_n)$,那么就可以列出 $(n+1)$ 个方程:
$(b_1 - a_{11})^2 + (b_2 - a_{12})^2 + … + (b_n - a_{1n})^2 = R^2$ …
但是这并不是线性方程组。
为了使其成为线性方程组,将 $(n+1)$ 个方程进行相减,得到
- 方程 $2$ 减去方程 $1$
- 方程 $3$ 减去方程 $1$ …
即可得到 $n$ 个线性方程。
然后用高斯消元即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 12;
double A[maxn][maxn], arr[maxn][maxn];
int n;
void solve() {
for (int k = 1; k <= n; k++) {
int maxrow = k;
for (int i = k+1; i <= n; i++) {
if (abs(A[i][k]) > abs(A[maxrow][k])) maxrow = i;
}
for (int i = 1; i <= n+1; i++) swap(A[k][i], A[maxrow][i]); //交换两行, 保证A[k][k]最大
if (abs(A[k][k]) < eps) {
cout << "No Solution" << endl;
return;
}
for (int i = 1; i <= n; i++) {
if (i == k) continue;
double m = A[i][k] / A[k][k];
for (int j = 1; j <= n+1; j++) { //更新上下的行
A[i][j] -= (m * A[k][j]);
}
}
}
for (int i = 1; i <= n; i++) {
A[i][n+1] /= A[i][i]; // 最后除以斜线上的系数
A[i][i] = 1.0;
printf("%.3f ", A[i][n+1]);
}
}
double sq(double a) {
return a*a;
}
int main() {
cin >> n;
for (int i = 1; i <= n+1; i++) {
for (int j = 1; j <= n; j++) {
cin >> arr[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
A[i][j] = arr[i+1][j] - arr[i][j];
}
for (int k = 1; k <= n; k++) {
A[i][n+1] += sq(arr[i+1][k]) - sq(arr[i][k]);
}
A[i][n+1] /= 2;
}
solve();
}
例3 NAQ2016 B. Arcade!
题意
给定一个金字塔形的棋盘,有 $n$ 行,第 $i$ 行有 $i$ 个洞。
一个球在一个洞时,有 $p_0,p_1,p_2,p_3$ 的概率分别往左上,右上,左下,右下的洞跳。也有 $p_4$ 的概率掉入当前这个洞,获得 $v_i$ 的收益,并且游戏结束,如果某个操作不合法,那么对应的概率为 $0$。
从洞 $1$ 出发,求最终的收益期望?
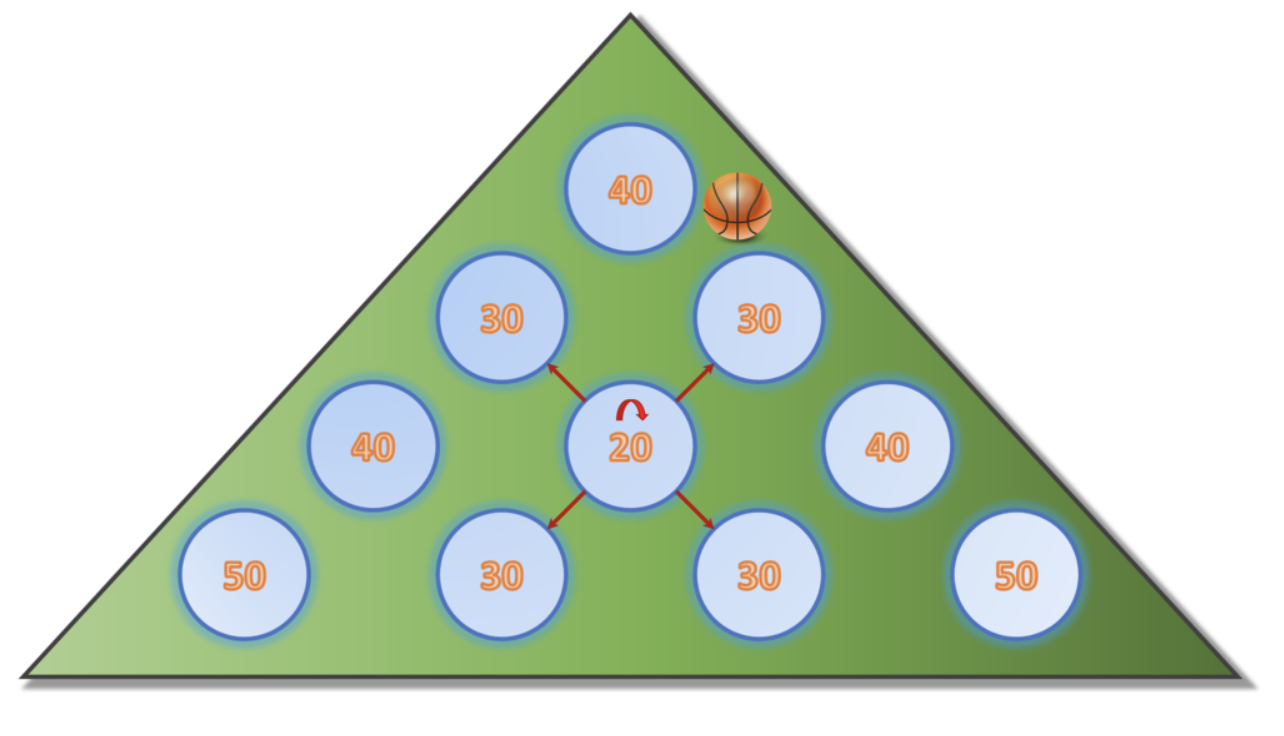
其中,$n \leq 32, p_0+p_1+p_2+p_3+p_4 = 1$。
题解
对于一个洞来说,设从它出发的最终收益期望为 $E$,那么有
$$E = E_0p_0 + E_1p_1 + E_2p_2 + E_3p_3 + vp_4$$
其中,$E_0$ 到 $E_3$ 分别代表四个方位的最终收益。
这样,可以列出来一个 $N \times N$ 的方程组,其中 $N = \frac{n(n+1)}{2}$。
高斯消元即可。
• 这个只能求收益期望,而不能求出最终掉入每个洞的概率。因为掉入每个洞的概率与 “从哪出发” 有关,所以需要两个维度来表示 dp 的状态(从哪出发 + 掉入哪个洞)。而收益期望仅和 ”从哪出发“ 有关,所以只需要一个维度。
代码
#include <bits/stdc++.h>
using namespace std;
struct GaussianElimination {
int n, m; // n: 行 (方程个数), m: 列 (变量个数)
double A[531][531];
GaussianElimination(int n, int m) : n(n), m(m) {}
vector<double> solve(int B = (int)1e6) {
// B: band 大小,指对于任意 A(i,j) != 0,若 i2-i > B || j2-i > B 则任意 A(i2,j2) = 0;若 B = 1e6 则无此限制
// 返回 x_1, x_2, ..., x_m (注意返回的长度为 m+1),所以 x_1 = ans[1]
vector<double> ans(m+1, 0);
vector<int> var, free_var; // 主元,自由元
int row = 1;
for (int col = 1; col <= m; col++) {
int maxrow = row;
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (abs(A[i][col]) > abs(A[maxrow][col])) { // 在 mod 情况下找到一个非0即可
maxrow = i;
}
}
if (abs(A[maxrow][col]) < eps) {
// 自由元, 跳过这个 col,但row不变
free_var.push_back(col);
continue;
} else { // 主元
var.push_back(col);
}
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) swap(A[row][j], A[maxrow][j]);
swap(A[row][m+1], A[maxrow][m+1]);
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (i == row) continue;
double in = A[i][col] / A[row][col];
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) {
A[i][j] -= (in * A[row][j]);
}
A[i][m+1] -= (in * A[row][m+1]);
}
// printall();
row++; // 增加 row
}
row--; // 因为row是从1开始的,所以会多加一次 (现在 [1,row] 代表了主元)
assert(row == var.size());
if (row < n) { // 要么无解,要么有无数多个解
for (int i = row + 1; i <= n; i++) {
if (abs(A[i][m+1]) > eps) return {}; // 无解
}
// 否则,有无数多个解,将自由元设为 0,输出主元的解
}
// 有解 和 无数个解 都输出了
for (int i = row; i >= 1; i--) {
// 此时,主元是 var[i-1]
int k = var[i-1];
for (int j = k+1; j <= min(m, k+2*B); j++) {
A[i][m+1] -= A[i][j] * ans[j];
A[i][j] = 0;
}
ans[k] = A[i][m+1] / A[i][k];
}
return ans;
}
};
int n, id[33][33], v[33*33];
vector<pii> dir {{-1,-1}, {-1,0}, {1,0}, {1,1}};
int main() {
cin >> n;
int N = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
id[i][j] = ++N;
cin >> v[N];
}
}
GaussianElimination ge(N, N);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
int u = id[i][j];
for (int o = 0; o < 4; o++) {
double p; cin >> p;
int pi = i + dir[o].first, pj = j + dir[o].second;
if (pi >= 1 && pi <= n && pj >= 1 && pj <= n) {
int v = id[pi][pj];
ge.A[u][v] = p;
}
}
ge.A[u][u] = -1;
double p; cin >> p;
ge.A[u][N+1] = -p * v[u];
}
}
auto ans = ge.solve(N*2+2);
printf("%.10f\n", ans[1]);
}
例4 NAQ2016I. Primonimo
题意
给定一个 $n \times m$ 的矩阵,和一个质数 $p$。
矩阵中每一个数在 $[1,p]$ 之间。
现在可以进行若干次操作,每次操作选择一个位置 $(i,j)$,然后给第 $i$ 行上的所有数字 + 1,并且给第 $j$ 列上的所有数字 + 1,其中 $(i,j)$ 本身也只加一次。
如果数字 $p$ 再加1,则它会变回 $1$。
求是否存在一种方案,使得所有的数都变成 $p$,输出这个方案,如果有多种,输出任意方案。
其中,$n,m \leq 20, p \in [2,97]$。
题解
对于每一个格子 $(x,y)$,我们可以知道它需要被加多少次,设它为 $c_{x,y}$。
我们设 $f_{x,y}$ 为我们需要对位置 $(x,y)$ 进行的操作次数,那么有
$$\sum\limits_{i=1}^n f_{i,y} + \sum\limits_{j=1}^m f_{x,j} - f_{x,y} = c_{x,y}$$
这样又可以列出一个 $N \times N$ 的方程,其中 $N= n \times m$。
• 不过这个方程是在mod意义下的,但不影响,正常来解即可。除法就变成乘逆元。
代码
#include <bits/stdc++.h>
using namespace std;
int P, g[21][21], n, m, id[21][21], cid = 0;
struct GaussianElimination {
int n, m; // n: 行 (方程个数), m: 列 (变量个数)
Z A[403][403];
GaussianElimination(int n, int m) : n(n), m(m) {}
vector<Z> solve(int B = (int)1e6) {
// B: band 大小,指对于任意 A(i,j) != 0,若 i2-i > B || j2-i > B 则任意 A(i2,j2) = 0;若 B = 1e6 则无此限制
// 返回 x_1, x_2, ..., x_m (注意返回的长度为 m+1),所以 x_1 = ans[1]
vector<Z> ans(m+1, 0);
vector<int> var, free_var; // 主元,自由元
int row = 1;
for (int col = 1; col <= m; col++) {
int maxrow = row;
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (A[i][col].val()) { // 在 mod 情况下找到一个非0即可
maxrow = i;
break;
}
}
if (!A[maxrow][col].val()) {
// 自由元, 跳过这个 col,但row不变
free_var.push_back(col);
continue;
} else { // 主元
var.push_back(col);
}
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) swap(A[row][j], A[maxrow][j]);
swap(A[row][m+1], A[maxrow][m+1]);
for (int i = row+1; i <= min(n, row+2*B); i++) {
if (i == row) continue;
Z in = A[i][col] / A[row][col];
for (int j = max(1, col-2*B); j <= min(m, col+2*B); j++) {
A[i][j] -= (in * A[row][j]);
}
A[i][m+1] -= (in * A[row][m+1]);
}
row++; // 增加 row
}
row--; // 因为row是从1开始的,所以会多加一次 (现在 [1,row] 代表了主元)
assert(row == var.size());
if (row < n) { // 要么无解,要么有无数多个解
for (int i = row + 1; i <= n; i++) {
if (A[i][m+1].val()) return {}; // 无解
}
// 否则,有无数多个解,将自由元设为 0,输出主元的解
}
// 有解 和 无数个解 都输出了
for (int i = row; i >= 1; i--) {
// 此时,主元是 var[i-1]
int k = var[i-1];
for (int j = k+1; j <= min(m, k+2*B); j++) {
A[i][m+1] -= A[i][j] * ans[j];
A[i][j] = 0;
}
ans[k] = A[i][m+1] / A[i][k];
}
return ans;
}
};
int main() {
cin >> n >> m >> mod;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
id[i][j] = ++cid;
}
}
GaussianElimination ge(n*m, n*m);
cid = 0;
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= m; b++) {
++cid;
for (int i = 1; i <= n; i++) {
ge.A[cid][id[i][b]] = 1;
}
for (int j = 1; j <= m; j++) {
ge.A[cid][id[a][j]] = 1;
}
ge.A[cid][n*m+1] = (Z)(mod - g[a][b]);
}
}
vector<Z> ans = ge.solve();
if (!ans.size()) {
cout << -1 << endl;
return 0;
}
vector<int> res;
for (int i = 1; i <= cid; i++) {
int j = ans[i].val();
while (j--) {
res.push_back(i);
}
}
cout << res.size() << endl;
for (int x : res) cout << x << " ";
cout << "\n";
}
例5 CF24D Broken robot
题意
给定一个 $n \times m$ 的矩阵,初始在 $(x,y)$,每次等概率的往左,右,下走或原地不动,但不能走出去(非法操作的话概率为 0),问走到最后一行期望的步数。
其中,$n,m \leq 10^3$。
题解
$n,m \leq 10^3$,不能直接列方程,否则有 $N=10^6$ 个方程,复杂度是 $O(N^3)$ 的。
不过注意到,只能往下走,不能往上走。所以第 $i$ 行的每个格子的期望只与第 $i+1$ 行有关。
从下往上推,在 第 $i$ 行时,第 $i+1$ 行都是常量了。
所以高斯消元只有 $m$ 个变量和 $m$ 个方程,但 $O(m^3)$ 仍然接受不了。
可以发现这是一个带状矩阵,每个变量只与它附近的两个变量有关,所以 $B=2$,可以 $O(mB^2)$ 进行一次高斯消元。
要进行 $n$ 次高斯消元,所以总复杂度是 $O(nmB^2)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, x, y;
double dp[maxn][maxn];
int main() {
cin >> n >> m >> x >> y;
GaussianElimination ge(m, m);
for (int i = n-1; i >= x; i--) {
for (int j = 1; j <= m; j++) {
ge.A[j][j] = ge.A[j][m+1] = 0;
}
if (m > 1) {
for (int j = 1; j <= m; j++) {
if (j == 1) {
ge.A[j][j] = 2.0 / 3, ge.A[j][j+1] = -1.0 / 3, ge.A[j][m+1] = dp[i+1][j] / 3 + 1;
} else if (j == m) {
ge.A[j][j] = 2.0 / 3, ge.A[j][j-1] = -1.0 / 3, ge.A[j][m+1] = dp[i+1][j] / 3 + 1;
} else {
ge.A[j][j] = 3.0 / 4, ge.A[j][j-1] = -1.0 / 4, ge.A[j][j+1] = -1.0 / 4, ge.A[j][m+1] = 1.0 / 4 * dp[i+1][j] + 1;
}
}
auto res = ge.solve(2);
for (int j = 1; j <= m; j++) dp[i][j] = res[j];
} else {
dp[i][1] = dp[i+1][1] + 2;
}
}
printf("%.10lf\n", dp[x][y]);
}
