基环树
Contents
定义
基环树指的是一个 $n$ 个节点,$n$ 条边的联通图。
叫基环树的原因是:给定一棵树,在这棵树上加上 任意一条边,就可以形成一个基环树了。
基环树的性质很优秀,比如:
- 去掉环上的任意一条边,就可以转化为一棵树。
- 基环树可以看作一个环上挂了很多棵子树,如果将环缩成一个点,那么得到的就是一棵树。
所以基环树的常用套路有:
- 找环,然后删掉环上的任意一条边 $(u,v)$,对 $u$ 为根的树进行一次树形DP(并强制不选 $u$),再对 $v$ 为根的树进行一次树形DP(并强制不选 $v$)。
- 将环缩成一个点,然后分类讨论答案是否经过环两种情况。
例1 洛谷P2607 [ZJOI2008]骑士
题意
给定 $n$ 个骑士,每个骑士有一个能力值 $a_i$,和他的一个痛恨的人 $b_i$(痛恨的人不能是自己)。
从这些骑士中选出若干个,使得两两之间没有痛恨的人,求出最大的能力值总和。
其中,$n \leq 10^6$。
题解
按照每个人 $i$ 与他痛恨的人 $b_i$ 连边,这就可以形成一个基环森林了(由多个基环树组成的森林)。
现在,只考虑一个基环树的话怎么办?
首先发现,如果断开一条边,在树上考虑这个问题的话,就是一个非常简单的树形DP了。
所以我们不妨断开环上的任意一条边 $(u,v)$。
然后以 $u$ 为根,在这个新的树上进行一次树形DP,并强制不选 $u$。
同理,以 $v$ 为根,在这个新的树上进行一次树形DP,并强制不选 $v$。
求两次树形DP得出的最大值即可。
最终答案就是每个基环树求出的最大值之和。
找环的话,只要发现一个 backward edge,记录一下这个 edge 的编号 E,标记一下 E 和 E^1,在树形DP中避开这两条边,就可以达到断开边的效果了。这要求我们建图时,使用 ecnt = 2。
• 需要格外注意一下,在断边的时候,必须判断当前枚举的边 e 是否等于 E 或者 E^1,而不能判断边的两端端点,这是防止出现 $(1,2), (2,1)$ 这种情况,可以参考这里。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int n, head[maxn], ecnt = 2;
ll a[maxn];
struct Edge {
int to, nxt;
} edges[maxn<<1];
void addEdge(int u, int v) {
Edge e = {v, head[u]};
head[u] = ecnt;
edges[ecnt++] = e;
}
int ed, dep[maxn], par[maxn], E;
void dfs1(int u) {
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[u]) continue;
if (dep[to]) {
E = e;
} else {
dep[to] = dep[u] + 1;
par[to] = u;
dfs1(to);
}
}
}
ll ans = 0, tot = 0;
ll dp[maxn][2];
void dfs2(int u, int p) {
dp[u][0] = 0;
dp[u][1] = a[u];
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == p || e == E || e == (E^1)) continue;
dfs2(to, u);
dp[u][0] += max(dp[to][0], dp[to][1]);
dp[u][1] += dp[to][0];
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
int v;
cin >> a[i] >> v;
addEdge(i,v); addEdge(v,i);
}
for (int u = 1; u <= n; u++) {
if (!dep[u]) {
ans = 0; E = 0;
dep[u] = 1;
dfs1(u);
int c1 = edges[E].to, c2 = edges[E^1].to;
dfs2(c1, 0);
ans = max(ans, dp[c1][0]);
dfs2(c2, 0);
ans = max(ans, dp[c2][0]);
tot += ans;
}
}
cout << tot << endl;
}
例2 洛谷P4381 [IOI2008] Island
题意
给定一个基环树组成的森林,每条边上有边权,求出每个基环树的最长链的长度之和。
最长链的定义为:一条路径,不经过重复的节点。
其中,$n \leq 10^6$。
题解
既然是基环森林,那就只考虑每个基环树怎么求最长链。
注意到一个基环树由一个环,以及每个环的子树组成,长这样:
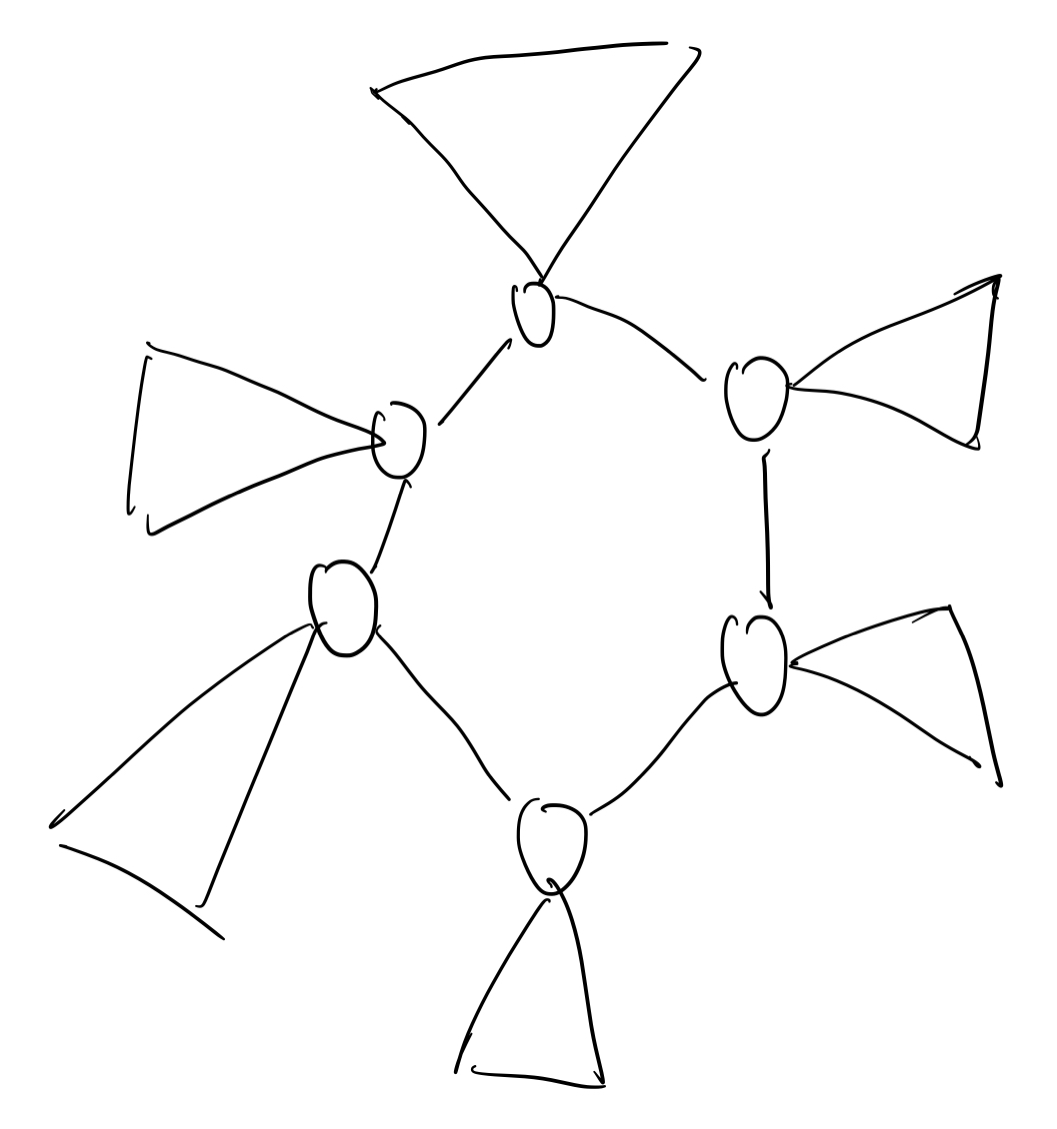
所以我们可以讨论这个最长链的位置:
第一种情况:最长链不经过环
这说明最长链完全在一个子树内,那么这就是一个树的直径问题。
第二种情况:最长链经过环
如果经过了环,我们设它从环上的某个点 $u$ 的子树开始,到环上另外一个点 $v$ 的子树结束。
并且设 $dis(u,v)$ 为 $u,v$ 在环上的最长距离,设 $d(u)$ 为 $u$ 的子树最大深度。
所以答案就是
$$\max_{(u,v)}\{d(u)+d(v)+dis(u,v)\}$$
但找这样的 $(u,v)$ 是 $O(n^2)$ 的,考虑一下如何优化?
如果我们将一个环 $1,2,3,…,n$ 断开,并复制一份,得到 $1,2,3,…,n,1’,2’,3’,…,n'$,则我们可以快速的算出 $dis(u,v)$。
不妨设 $u<v$,并且求一个距离的前缀和 $a[]$,其中 $a[i]=a[i-1]+w(i-1,i)$。
那么
$$\max_{(u,v)}\{d(u)+d(v)+dis(u,v)\}$$
就可以写成
$$\max_{(u,v)}\{d(u)+d(v)+a[v]-a[u]\}, u,v\in[1,n] \cup [1’,n’], (v-u) \in [1, n-1]$$
当 $v$ 确定时,我们要求的实际上就是
$$\max_u \{d(u) - a[u]\}, u \in [v-n+1,v-1]$$
这就是个单调队列优化dp。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
struct Edge {
int from, to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 2, in[maxn];
void addEdge(int u, int v, ll w) {
Edge e = {u, v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
bool vis[maxn], ring[maxn];
ll ans = 0;
// solve the component containing u
vector<int> ver; // vertex in current component
void bfs(int u) {
vis[u] = 1;
ver.push_back(u);
int p = 0;
while (p < ver.size()) {
int v = ver[p];
for (int e = head[v]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (vis[to]) continue;
vis[to] = 1;
ver.push_back(to);
}
p++;
}
}
ll dep[maxn], maxdep[maxn];
vector<int> tmp; // used for storing leaf
int maxi = 0, n;
int q[maxn<<1], hd, tail, par[maxn];
void bfs2(int u) {
int o = u;
hd = 1, tail = 0;
q[++tail] = u;
par[u] = 0;
dep[u] = 0;
while (hd <= tail) {
u = q[hd]; hd++;
if (dep[u] > dep[maxi]) maxi = u;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[u] || ring[to]) continue;
par[to] = u;
q[++tail] = to;
dep[to] = dep[u] + edges[e].w;
}
}
maxdep[o] = dep[maxi];
}
ll md = 0;
void bfs3(int u, int v) {
hd = 1, tail = 0;
q[++tail] = u;
par[u] = 0;
dep[u] = 0;
while (hd <= tail) {
u = q[hd]; hd++;
md = max(md, dep[u]);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[u] || (ring[to] && to != v)) continue;
par[to] = u;
q[++tail] = to;
dep[to] = dep[u] + edges[e].w;
}
}
}
vector<int> rings;
bool tag[maxn<<1];
struct Node {
ll a, d;
} nd[maxn<<1];
bool del[maxn];
void solve(int u) {
ver.clear();
tmp.clear();
bfs(u);
ll res = 0;
for (int v : ver) {
if (in[v] == 1) tmp.push_back(v);
}
while (!tmp.empty()) {
int v = tmp.back(); tmp.pop_back();
del[v] = 1;
for (int e = head[v]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (!del[to]) {
in[v]--; in[to]--;
if (in[to] == 1) tmp.push_back(to);
}
}
}
for (int v : ver) {
if (in[v] >= 2) ring[v] = 1; // v is on the ring
}
rings.clear();
int cnt = 0;
for (int v : ver) {
if (ring[v]) {
cnt++;
if (!rings.size()) rings.push_back(v);
maxi = 0;
md = 0;
bfs2(v);
dep[maxi] = 0;
bfs3(maxi, v);
res = max(res, md);
hd = 1, tail = 0;
}
}
// get the ring
if (rings.size()) {
while (rings.size() < cnt) {
int v = rings.back();
for (int e = head[v]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (!ring[to] || (rings.size() > 1 && to == rings[rings.size()-2])) continue;
if (to == rings[0]) {
goto done;
}
rings.push_back(to);
break;
}
}
}
done:;
int ptr = 0;
if (rings.size()) {
rings.push_back(rings.front());
nd[++ptr] = {0, maxdep[rings[0]]};
}
int m = rings.size();
for (int i = 0; i < m-1; i++) {
int v = rings[i];
int v2 = rings[i+1];
for (int e = head[v]; e; e = edges[e].nxt) {
if (edges[e].to == v2 && !tag[e]) {
ll w = edges[e].w;
nd[ptr+1].a = nd[ptr].a + w;
nd[ptr+1].d = maxdep[v2];
ptr++;
tag[e] = tag[e^1] = 1; // 标记边,防止有大小为2的环!
break;
}
}
}
for (int i = 0; i < m-2; i++) {
nd[ptr+1].a = nd[ptr].a + (nd[i+2].a - nd[i+1].a);
nd[ptr+1].d = maxdep[rings[i+1]];
ptr++;
}
hd = 1, tail = 0;
q[++tail] = 1;
m--; // now: m is the size of the ring
for (int i = 2; i <= ptr; i++) {
while (hd <= tail && i - q[hd] >= m) hd++;
if (hd <= tail) {
res = max(res, nd[i].a + nd[i].d + nd[q[hd]].d - nd[q[hd]].a);
}
while (hd <= tail && nd[i].d - nd[i].a >= nd[q[tail]].d - nd[q[tail]].a) tail--;
q[++tail] = i;
}
ans += res;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
int v; ll w; cin >> v >> w;
addEdge(i,v,w); addEdge(v,i,w);
in[i]++; in[v]++;
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
solve(i);
}
}
cout << ans << endl;
}
注意点
- 所有的树上/图上操作(包括找树的直径)都必须用
bfs进行,因为 $n \leq 10^6$,dfs会爆栈。 - 找环的时候用拓扑排序,不过注意这个是无向图,所以写法略有不同。
- 找出环以后,要按照环的顺序把环断开,不能只考虑哪些节点在环上而不考虑顺序。
- 一定要注意 大小为 $2$ 的环,我们在断环为链的时候不能考虑节点之间的关系,而是要标记 edge,因为双向图的缘故,大小为 $2$ 的环之间会有重边,一定要注意!
例3 洛谷P1399 [NOI2013] 快餐店
题意
给定一个 $n$ 个节点,$n$ 条边的无向图(基环树),边上有权值。
现在要在树上找一个位置 $x$,这个位置 $x$ 可以位于边上的任意一处,也可以位于节点上。
如何选择 $x$ 的位置,使得它到 所有节点的最短距离的最大值 最小?输出这个最小值。
形式化的,求:
$$\min_x \{\max_u\{dis(x,u)\}\}$$
其中,$n \leq 10^5$。
题解
先考虑,如果这是一棵树的话怎么办?
那我们只要求出这棵树的直径,然后答案就是 直径/2 了。
对于基环树,我们一般都是断环,得到一棵树,那么对于这个题我们有类似的想法:
猜想:环上必然存在一条边,使得这条边断开以后对整个答案没有任何影响。
证明:我们考虑 $x$ 的位置
- $x$ 在环上
- $x$ 在一棵子树中
对于第一种情况,我们注意到 $x$ 到所有节点的最短路径中,由环上路径和树内路径组成。
我们只考虑环上的路径(因为我们要证明的是环上的所有边不可能都被用到,至少有一个是用不上的)。
那么问题就相当于,$x$ 到环上所有节点的最短路径,是否存在一条边用不上?
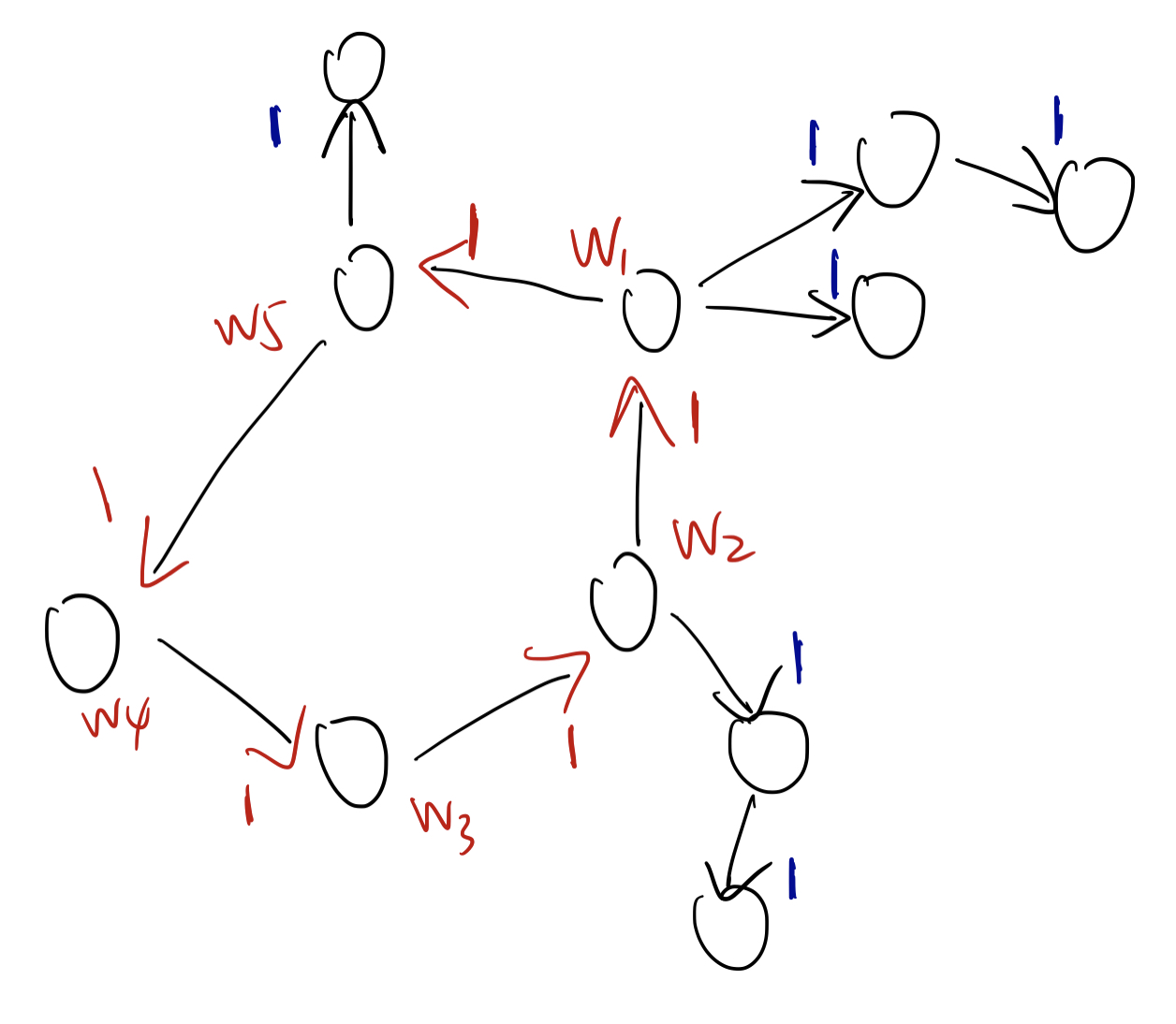
确实如此,因为无论我们怎么画,都会有一条边被断开以后没有任何影响,如图:
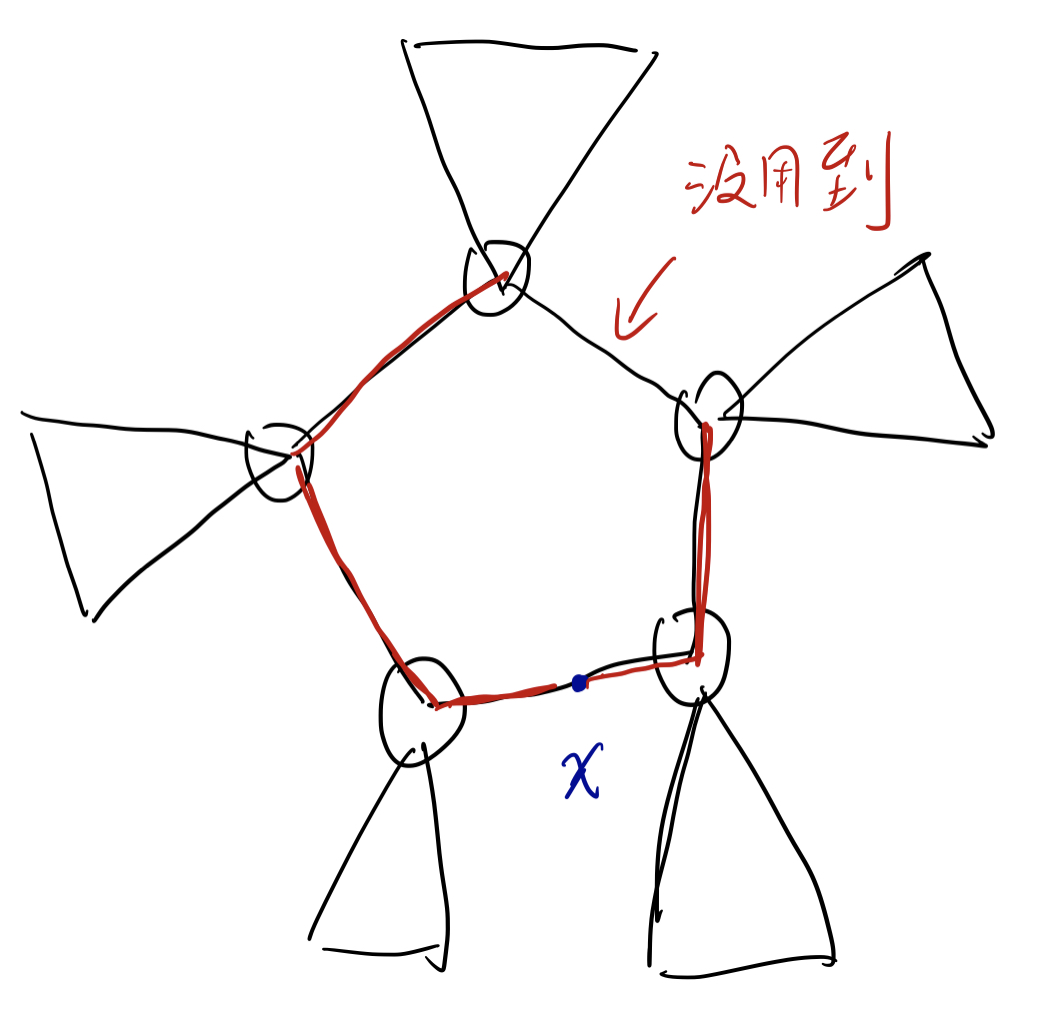
• 对于第二种情况也完全一样,所以这个结论是正确的。
所以问题就转化成了:
给定一棵基环树,我们现在要断开环上的一条边,求所有断开的方案中,树的直径最小的一个方案,求出最小值?
然后这题就和上一个例子差不多了,一样分类讨论直径在哪:
- 断开后,树的直径在子树内
- 断开后,树的直径在原先的环上
对于第一种情况,无论断开哪个都不影响答案,所以对于每个子树统计一下直径即可。
对于第二种情况,上一题的单调队列套路不好使了,我们形式化的描述一下这个问题:
给定一个环 $1,2,…,n$,对于每一种断环方案,都求出:
$$\max_{(u,v)}\{d(u)+d(v)+dis(u,v)\}$$
然后取所有断环方案对应的最小值。
这里有了个断环方案要讨论,就变得非常不友好,就算断环成链也没什么思路,我们考虑另外一种方法:
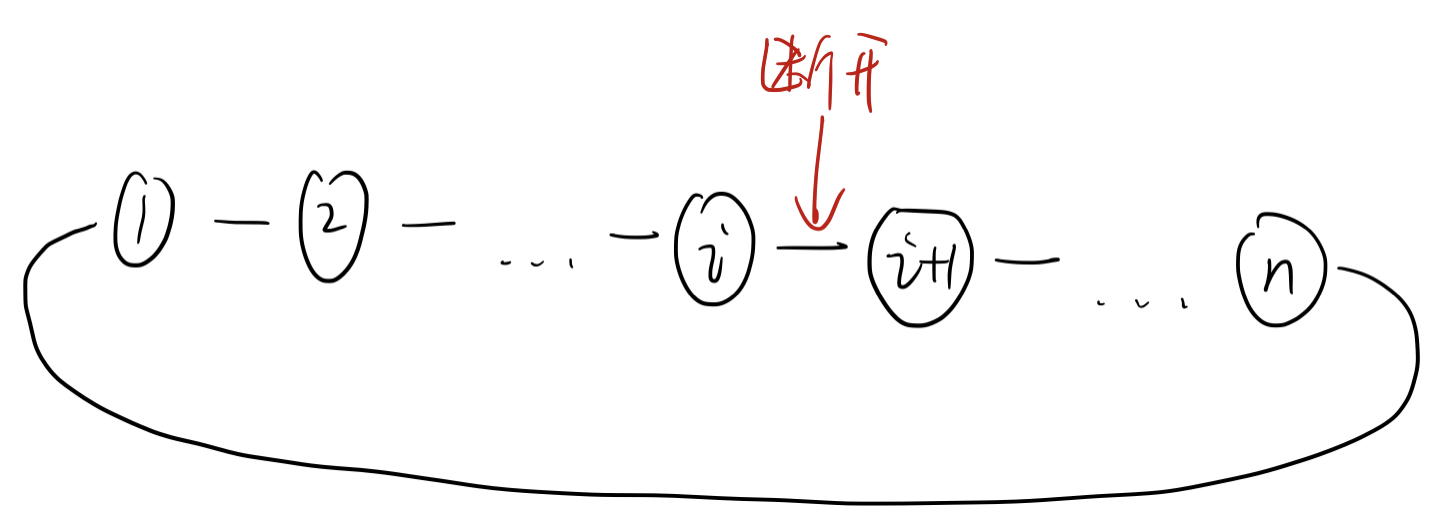
假设我们要断开 $(i,i+1)$,那么此时,这个所求的最大值对应的 $(u,v)$ 有几种情况呢?
- $(u,v)$ 都在 $[1,i]$ 内。
- $(u,v)$ 都在 $[i+1,n]$ 内。
- $u$ 在 $[1,i]$,$v$ 在 $[i+1,n]$。
对于第一种,我们同样用前缀和的方式来看,因为 $dis(u,v) = sum(v) - sum(u)$,所以和上一题一样处理一个前缀和即可,本题甚至都不需要单调队列,维护一下前缀的 -sum[u] + d[u] 的最大值即可。
然后我们就可以处理出一个 pre[] 数组,pre[i] 的意思就是如果 $(u,v)$ 都在 $[1,i]$ 内,可以得到的最大值。
同理对于第二种我们用后缀处理一下即可,可以得到 suf[]。
对于第三种,我们可以发现我们所求的 $dis(u,v) + d(u) + d(v)$,等于
$u$ 的 前缀链 + $v$ 的 后缀链 + $w(n,1)$
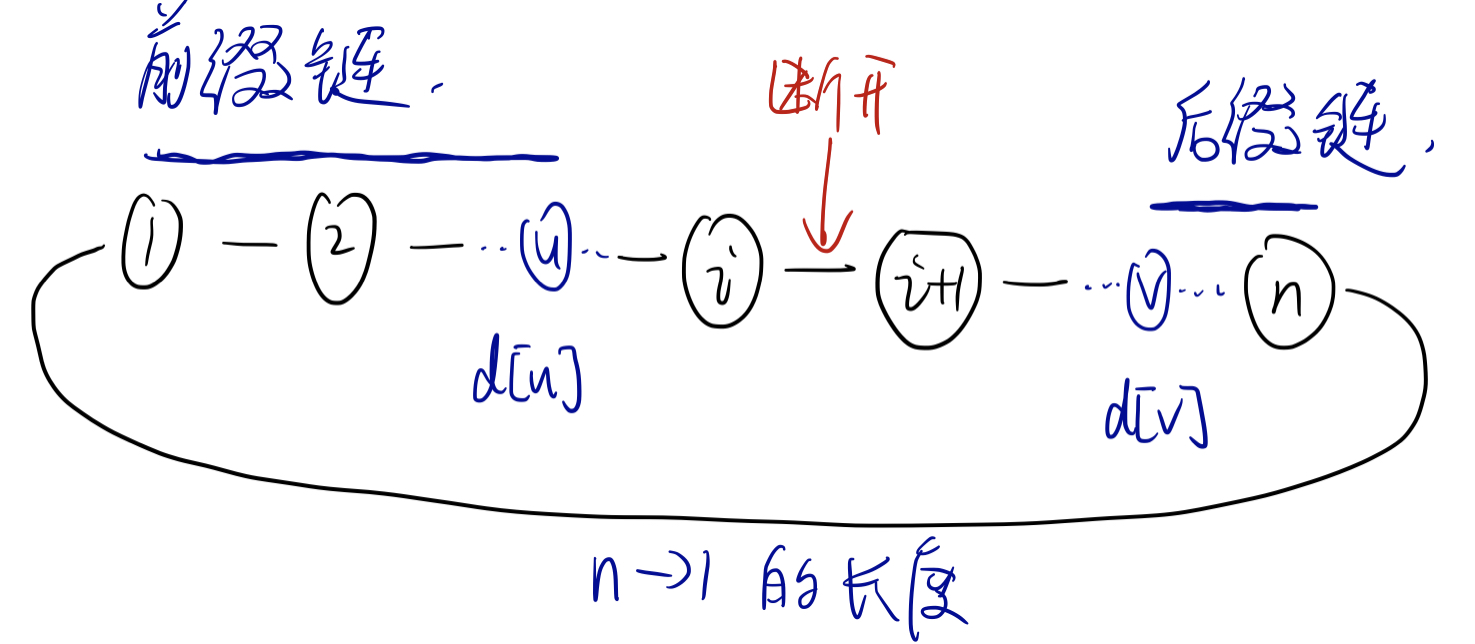
所以我们只要把这个前缀链的最大值 maxl[i] 求出即可(同理后缀链最大值也求出 maxr[])。
那么,当我们断开 $(i,i+1)$ 时,就有
$$\max_{(u,v)}\{d(u)+d(v)+dis(u,v)\} = \max\{pre(i), suf(i+1), maxl(i) + maxr(i+1) + w(n,1)\}$$
然后将 $i$ 从 $1$ 枚举到 $n$ 即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
struct Edge {
int from, to, nxt;
ll w;
} edges[maxn<<1];
int head[maxn], ecnt = 2, in[maxn];
void addEdge(int u, int v, ll w) {
Edge e = {u, v, head[u], w};
head[u] = ecnt;
edges[ecnt++] = e;
}
bool ring[maxn];
ll ans = 0;
ll dep[maxn], maxdep[maxn];
vector<int> tmp; // used for storing leaf
int maxi = 0, n;
int q[maxn<<1], hd, tail, par[maxn];
void bfs2(int u) {
int o = u;
hd = 1, tail = 0;
q[++tail] = u;
par[u] = 0;
dep[u] = 0;
while (hd <= tail) {
u = q[hd]; hd++;
if (dep[u] > dep[maxi]) maxi = u;
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[u] || ring[to]) continue;
par[to] = u;
q[++tail] = to;
dep[to] = dep[u] + edges[e].w;
}
}
maxdep[o] = dep[maxi];
}
ll md = 0;
void bfs3(int u, int v) {
hd = 1, tail = 0;
q[++tail] = u;
par[u] = 0;
dep[u] = 0;
while (hd <= tail) {
u = q[hd]; hd++;
md = max(md, dep[u]);
for (int e = head[u]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (to == par[u] || (ring[to] && to != v)) continue;
par[to] = u;
q[++tail] = to;
dep[to] = dep[u] + edges[e].w;
}
}
}
vector<int> rings;
bool tag[maxn<<1];
struct Node {
ll a, d;
} nd[maxn<<1];
bool del[maxn];
ll maxl[maxn], maxr[maxn], pre[maxn], suf[maxn];
void solve() {
ll res = 0;
for (int v = 1; v <= n; v++) {
if (in[v] == 1) tmp.push_back(v);
}
while (!tmp.empty()) {
int v = tmp.back(); tmp.pop_back();
del[v] = 1;
for (int e = head[v]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (!del[to]) {
in[v]--; in[to]--;
if (in[to] == 1) tmp.push_back(to);
}
}
}
for (int v = 1; v <= n; v++) {
if (in[v] >= 2) ring[v] = 1; // v is on the ring
}
int cnt = 0;
for (int v = 1; v <= n; v++) {
if (ring[v]) {
cnt++;
if (!rings.size()) rings.push_back(v);
maxi = 0;
md = 0;
bfs2(v);
dep[maxi] = 0;
bfs3(maxi, v);
res = max(res, md);
hd = 1, tail = 0;
}
}
// get the ring
if (rings.size()) {
while (rings.size() < cnt) {
int v = rings.back();
for (int e = head[v]; e; e = edges[e].nxt) {
int to = edges[e].to;
if (!ring[to] || (rings.size() > 1 && to == rings[rings.size()-2])) continue;
if (to == rings[0]) {
goto done;
}
rings.push_back(to);
break;
}
}
}
done:;
int ptr = 0;
if (rings.size()) {
rings.push_back(rings.front());
nd[++ptr] = {0, maxdep[rings[0]]};
}
int m = rings.size();
for (int i = 0; i < m-1; i++) {
int v = rings[i];
int v2 = rings[i+1];
for (int e = head[v]; e; e = edges[e].nxt) {
if (edges[e].to == v2 && !tag[e]) {
ll w = edges[e].w;
nd[ptr+1].a = nd[ptr].a + w;
nd[ptr+1].d = maxdep[v2];
ptr++;
tag[e] = tag[e^1] = 1; // 标记边,防止有大小为2的环!
break;
}
}
}
for (int i = 0; i < m-2; i++) {
nd[ptr+1].a = nd[ptr].a + (nd[i+2].a - nd[i+1].a);
nd[ptr+1].d = maxdep[rings[i+1]];
ptr++;
}
hd = 1, tail = 0;
ll R = res;
res = 1e18;
m--; // now: m is the size of the ring
// maxl: record a+d
for (int i = 1; i <= m; i++) maxl[i] = max(maxl[i-1], nd[i].a + nd[i].d);
for (int i = m; i >= 1; i--) maxr[i] = max(maxr[i+1], nd[m+1].a - nd[i].a + nd[i].d);
// pre: record the maximum of two i,j <= pre, which dis(i,j) + d[i] + d[j] is maximum (just record minimum of -a + d)
ll mn = 0;
for (int i = 1; i <= m; i++) {
pre[i] = max(pre[i-1], mn + nd[i].a + nd[i].d);
mn = max(mn, -nd[i].a + nd[i].d);
}
mn = 0;
for (int i = m; i >= 1; i--) {
suf[i] = max(suf[i+1], mn + nd[m+1].a - nd[i].a + nd[i].d);
mn = max(mn, -(nd[m+1].a - nd[i].a) + nd[i].d);
}
for (int i = 1; i <= m; i++) { // break (i,i+1)
ll r1 = 0, r2 = 0;
r1 = max(pre[i], suf[i+1]);
r2 = maxl[i] + maxr[i+1];
res = min(res, max(r1,r2));
}
ans += max(R, res);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
int u,v; ll w; cin >> u >> v >> w;
addEdge(u,v,w); addEdge(v,u,w);
in[u]++; in[v]++;
}
solve();
printf("%.1f\n",(double)(ans)*0.5);
}
例4 BAPC2022H. House Numbering
题意
给定一个 $n$ 个点,$n$ 条边的联通无向图。
每条边有一个权值 $w$,意味着这条边的两端需要分别标上 $1,w$ 或者 $w,1$。
问是否存在一种方案,使得所有点的边上没有被标上相同的元素。有,则输出方案。
其中,$n \leq 10^5$,所有边的 $w > 1$。
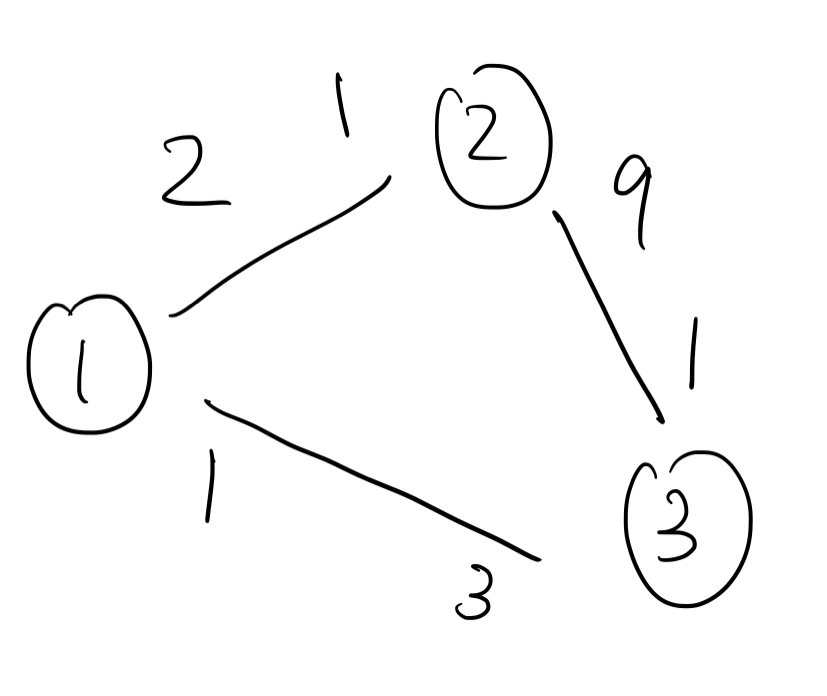
如图,这就是一种合理标号方式,其中 $w_{1,2}=2, w_{2,3}=9, w_{1,3}=3$。
题解
首先注意这是一个基环树。所以要围绕环做文章。
经过一段时间的观察后可以发现,如果我们把这个看作一个有向图,箭头指向的点会获得这个边的 $1$,另外一个点获得 $w$,那么所有不在环上的,都应该是向外指的。
因为一旦有一个向内指的,环上一旦出现一个来自于树的 $1$,那么就不成立了。
所以不在环上的部分都可以决定了。
剩下的只有环了。
可以发现环要么是顺时针指,要么是逆时针指,所以只要判断这两个情况就行。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n;
struct Edge {
int to, nxt, w;
int idx;
} edges[maxn<<1];
int head[maxn], ecnt = 2;
void addEdge(int u, int v, int w, int idx) {
Edge e = {v, head[u], w, idx};
head[u] = ecnt;
edges[ecnt++] = e;
}
bool iscycle[maxn];
bool vis[maxn];
int cu, cv, cidx, pre[maxn];
bool found = 0;
void dfs(int u) {
vis[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to, w = edges[e].w;
if (v == pre[u]) continue;
if (vis[v]) {
if (found) return;
found = 1;
int cur = u;
while (cur != v) {
iscycle[cur] = 1;
cur = pre[cur];
}
iscycle[v] = 1;
cu = u, cv = v;
cidx = edges[e].idx;
} else {
pre[v] = u;
dfs(v);
}
}
}
int ans[maxn];
void dfs2(int u, int p, int f) {
vis[u] = 1;
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to, w = edges[e].w, idx = edges[e].idx;
if (v == p) continue;
if (vis[v]) {
if (!found) ans[idx] = (f ? u : v), found = 1;
continue;
}
if (!iscycle[v]) { // then must point to v
ans[idx] = v;
} else {
assert(iscycle[u] && iscycle[v]);
if (f) {
ans[idx] = u;
} else {
ans[idx] = v;
}
}
dfs2(v, u, f);
}
}
bool check() {
for (int u = 1; u <= n; u++) {
set<int> se;
int cnt = 0;
for (int e = head[u]; e; e = edges[e].nxt) {
int v = edges[e].to, w = edges[e].w, idx = edges[e].idx;
if (ans[idx] == u) se.insert(1);
else se.insert(w);
cnt++;
}
if (se.size() != cnt) return 0;
}
return 1;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
int u,v,w; cin >> u >> v >> w;
addEdge(u,v,w,i);
addEdge(v,u,w,i);
}
dfs(1);
memset(vis, 0, sizeof(vis));
found = 0;
dfs2(cu, -1, 0); // start with any point on the cycle
if (check()) {
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << "\n";
return 0;
}
memset(vis, 0, sizeof(vis));
found = 0;
dfs2(cu, -1, 1); // start with any point on the cycle
if (check()) {
for (int i = 1; i <= n; i++) cout << ans[i] << " ";
cout << "\n";
return 0;
}
cout << "impossible\n";
}
