组合数学
Contents
本文主要记录一些组合数学的常用模型。
组合数 $C(n,m)$
- $C_n^0 = C_n^n = 1$
- $C_n^k = C_{n-1}^k + C_{n-1}^{k-1}$
- $C_n^k = \frac{n!}{k!(n-k)!}$
- $\sum\limits_{i=l}^r C_i^m = C_{r+1}^{m+1}-C_{l}^{m+1}$
• 注:$0! = 1, (0!)^{-1} = 1$
证明公式2
$n$ 个中选 $k$ 个, 考虑 $n$ 个元素中的第一个元素:
- 如果它被选中,有 $C_{n-1}^{k-1}$ 种。
- 如果它没有被选中,有 $C_{n-1}^k$ 种。
证明公式4
这个对应杨辉三角中的一列。
$C_{l}^{m+1} + \sum\limits_{i=l}^r C_i^m = (C_l^{m+1} + C_l^m) + \sum\limits_{i=l+1}^r = C_{l+1}^{m+1} + \sum\limits_{i=l+1}^r C_i^m = C_{l+2}^{m+1} + \sum\limits_{i=l+2}^r C_i^m = … = C_{r+1}^{m+1}$
杨辉三角

第 $i$ 行,第 $j$ 列的数就是 $C_{i-1}^{j-1}$。这个杨辉三角也可以用于证明二项式定理和组合数的一些性质。
二项式定理
$$(a+b)^n = \sum\limits_{k=0}^n C_n^ka^kb^{n-k}$$
卡特兰数 (Catalan)
通项公式:
-
$H_n = 1 ~ (n=0,1)$
-
$H_n = \frac{C_{2n}^n}{n+1}~(n \geq 2)$
-
$H_n = C_{2n}^n - C_{2n}^{n-1}$
递推式:
-
$H_n = \sum\limits_{i=0}^{n-1}H_{i}H_{n-i-1} = H_0H_{n-1} + H_1H_{n-2} + … + H_{n-1}H_0$
-
$H_n = \frac{(4n-2)}{n+1} H_{n-1}$
第二类斯特林数
$S(n,m)$ 代表将 $n$ 个不同的小球,放进 $m$ 个相同,非空盒子的方案数
通项公式:
$$S(n,m) = \sum\limits_{i=0}^m (-1)^{m-i}\frac{i^n}{i!(m-i)!}$$
递推式:
$$S(n,m) = m*S(n-1,m) + S(n-1,m-1)$$
证明
考虑第一个小球,有两种情况:
- 独占一个盒子:相当于,其他 $n-1$ 个小球要放进 $m-1$ 个盒子中,且盒子不为空,所以为 $S(n-1,m-1)$
- 不独占一个盒子:相当于,先将其他 $n-1$ 个小球放进 $m$ 个盒子中,且盒子不为空,然后从 $m$ 个盒子中选一个,把当前小球放进去,所以为 $m*S(n-1,m)$
经典例题
例1 男女生排列问题
题意
三个女生和五个男生站成一排。
-
如果女生必须全排在一起,有多少种排法?
-
如果女生不能相邻,有多少种排法?
-
如果两端都不排女生,有多少种排法?
-
如果两端不都排女生,有多少种排法?
第一题答案
将3个女生看作1个,所以就有 $A_6^6$ 种。对于女生内部的排列有 $A_3^3$ 种。所以总共为 $A_6^6A_3^3$ 种。
第二题答案
先排男生,有 $A_5^5$ 种,然后将女生插入6个空位中,有 $A_6^3$ 种。所以总共为 $A_5^5A_6^3$ 种。
第三题答案
先排好两个男生在两边,有 $A_5^2$ 种,两个男生中间的人就可以随便排了,就有 $A_6^6$ 种。所以总共为 $A_5^2A_6^6$ 种。
也可以这么想,让女生在中间的6个位置先选好3个,有 $A_6^3$ 种,剩下的男生随便排,有 $A_5^5$ 种。所以总共为 $A_6^3A_5^5$ 种,答案和上面一样。
第四题答案
所有排列情况有 $A_8^8$ 种,如果两边都排女生,有 $A_3^2A_6^6$ 种。所以总共为 $A_8^8 - A_3^2A_6^6$ 种。
例2 小球放盒子问题
假设有 $n$ 个小球,$m$ 个盒子,要将小球放进这些盒子中,每个小球都必须放入其中一个盒子中。
小球无区别-盒子无区别-不允许空盒
略(还没遇到)
小球无区别-盒子无区别-允许空盒
略(还没遇到)
小球无区别-盒子有区别-不允许空盒
使用隔板法,在 $n$ 个小球中间放置 $m-1$ 块挡板,将小球分为不为空的 $m$ 部分。小球之间的空位有 $n-1$ 个。所以答案为
$$C_{n-1}^{m-1}$$
小球无区别-盒子有区别-允许空盒
先多加 $m$ 个小球,转化为 不允许空盒 的问题后,再把多加的 $m$ 个小球拿出来即可。所以答案为
$$C_{n+m-1}^{m-1}$$
小球有区别-盒子无区别-不允许空盒
答案就是第二类斯特林数 $S(n,m)$,递推式如上:
$$S(n,m) = m*S(n-1,m) + S(n-1,m-1)$$
小球有区别-盒子无区别-允许空盒
在 不允许空盒 的基础上,枚举一下 空盒的个数。所以答案为
$$\sum\limits_{i=1}^{\min(n,m)}S(n,i)$$
小球有区别-盒子有区别-不允许空盒
在 盒子无区别 的基础上,乘上盒子的排列 $m!$ 即可,所以答案为:
$$S(n,m) * m!$$
小球有区别-盒子有区别-允许空盒
每个小球可以随便选,互不影响,所以答案为:
$$n^m$$
例3 整数解问题
题意
$$a_1+a_2+…+a_m = n$$
的解的个数,由此可以得出一系列的例题,如下:
$\forall i \in [1,m], a_i > 0$
这就是小球放盒子问题,盒子不为空的情况,用隔板法即可得到答案为在 $n$ 个小球之间放置 $m-1$ 个隔板,等于:
$$C_{n-1}^{m-1}$$
$\forall i \in [1,m], a_i \geq 0$
我们直接转化成:
$$a_1'+a_2'+…+a_m’ = n+m, ~~ \forall i \in [1,m], a_i’ > 0$$
其中 $a_i’ = a_i + 1$。
所以就可以套上面那种情况了,答案为:
$$C_{n+m-1}^{m-1}$$
求 $a_1+a_2+...+a_m < n$,其中 $\forall i \in [1,m], a_i > 0$
我们直接添加一个额外的正整数元素 $a_{m+1}$,问题转化为:
求
$$a_1+a_2+…+a_m+a_{m+1} = n, ~~\forall i \in [1,m+1], a_i > 0$$
又转化成了第一种情况,答案为:
$$C_{n-1}^m$$
$\forall i \in [1,m], a_i \geq 0$,且 $x_1 > 3, x_2 \in [4,8]$
我们往最基础的模型(第一种,第二种)情况上面转,也就是尽可能让 $x_i \geq 0$ 或者 $x_i > 0$ 对于所有 $i$ 都成立。
首先因为 $x_2 \in [4,8]$,所以我们如果令 $x_2 \geq 3$,只要减去 $x_2 \geq 9$ 的情况即可。
所以现在,我们先求出 $x_1 > 3, x_2 \geq 3$ 的情况即可。
由于 $x_1 > 3$,我们有 $x_1 \geq 4$,那么我们令 $x_1’ = x_1 - 4, x_2’ = x_2 - 3$,那么就可以得到 $x_1’ \geq 0, x_2’ \geq 0$。
所以我们只要求出:
$$a_1'+a_2'+…+a_m = n - 4 - 3 = n-7$$
其中每一项都 $\geq 0$ 即可。
所以方案数就是:$C_{n-7+m-1}^{m-1}$。
同理我们可以求出 $x_1 > 3, x_2 \geq 9$ 的情况,即为:
$$a_1'+a_2'+…+a_m = n - 4 - 9 = n-13$$
所以方案数就是:$C_{n-13+m-1}^{m-1}$。
两者相减,得到最终答案:
$$C_{n-7+m-1}^{m-1} - C_{n-13+m-1}^{m-1}$$
例4 错排问题
题意
有 $1,2,3,…,n$ 这些数字,重新排序使得不存在任何一个数字的位置和原来相同,有多少种方法?
答案
$$D_n = (n-1)(D_{n-1} + D_{n-2})$$
其中 $D_1 = 0, D_2 = 1$。
证明:初始情况下如图:
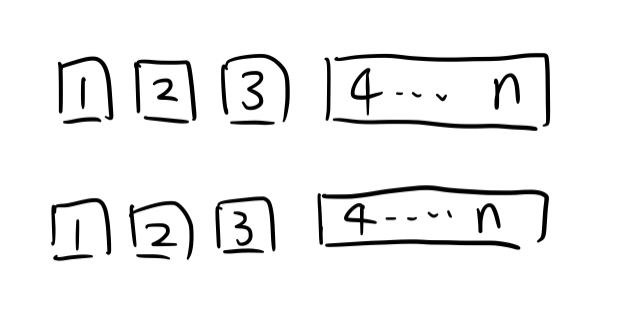
在图中,上下两行对应的元素需要错开。我们设这种情况下,排序的方法有 $f(n)$ 种。
对于元素 $1$,我们可以选择除 $1$ 以外的任何一个元素,所以有 $n-1$ 种。
假设我们选了 $1 \rightarrow 2$,就会变成下图:
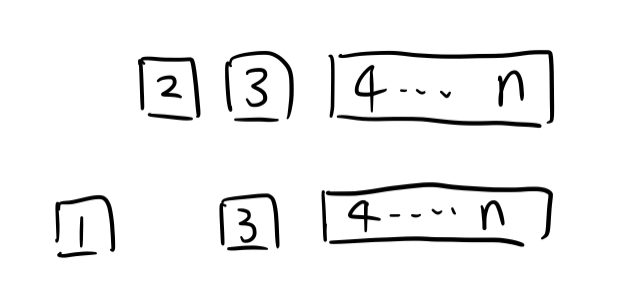
那么,再看元素 $2$:
-
如果 $2 \rightarrow 1$,那么就会变成下图,即 $f(n-2)$ 种。
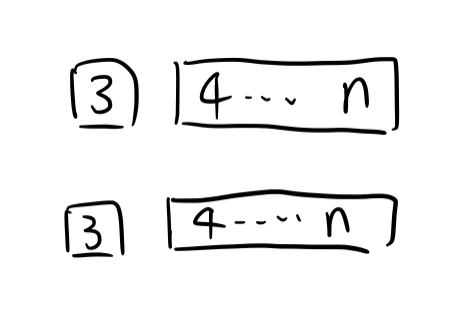
-
如果 $2 \rightarrow 3 ~ or ~ 4 ~ or ~ … ~ n$,就相当于 $2$ 和 $1$ 必须错开,那就相当于下图,即 $f(n-1)$ 种。
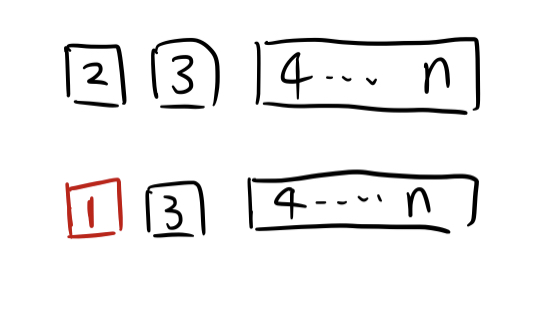
所以最终就可以得到 $f(n) = (n-1)(f(n-1) + f(n-2))$
例题
例1 CCPC威海2021 M题 810975
题意
求 $n$ 场比赛中,胜利 $m$ 场,最长连胜恰好为 $k$ 场的方案数?答案对 $998244353$ 取模。
其中,$n,m,k \in [0,10^5]$。
题解
首先让我们求最长连胜恰好为 $k$ 连胜的方案数,那么我们就转化成求 最长连胜 $\leq k$ 连胜的方案数,然后减去 $\leq (k-1)$ 的部分即可。
现在问题变成:
求 $n$ 场比赛中,胜利 $m$ 场,最长连胜 $\leq k$ 场的方案数?
那么我们往小球放盒子模型 / 整数解模型 上面转化,我们把一段连胜看作是一个数字,那么因为有 $(n-m)$ 个败场,每一段连胜就相当于插在这些败场的两侧。
所以就相当于有 $(n-m+1)$ 个盒子,我们把这些一段一段的胜场往盒子里面放。
也就是求:
$$a_1+a_2+…+a_{n-m+1} = m,~~ a_i \in [0,k]$$
的解数量。
为了方便,我们直接令 $n = n-m+1$,然后问题变成:
$$a_1+a_2+…+a_{n} = m,~~ a_i \in [0,k]$$
的解数量。
这个不是 $\geq 0$ 或者 $> 0$ 的形式,所以我们只能容斥来求。
首先我们有:
$$|\cap_{i=1}^n a_i \in [0,k]| = |a_i \geq 0| - |\cup_{i=1}^n a_i > k|$$
简单说就是 无限制 减去 至少有一个 $>k$ 的情况。
那么怎么求第二项,至少有一个 $>k$ 的情况?
由容斥原理我们可以得到:
$$|\cup_{i=1}^n a_i > k| = \sum\limits_{i=1}^n |a_i > k| - \sum\limits_{i<j,i,j\in [1,n]} |a_i > k \cap a_j > k| + … - … $$
那么对于右手边的第 $j$ 项,就相当于:
-
对于 $sum$ 符号,相当于:我们首先从 $n$ 项里面选择 $j$ 项出来,使得它们 $>k$,所以共有 $C_{n}^j$ 种选法(每一种选法,得到的方案数都一样,所以可以替代 sum)。
-
那么对于已经确定的 $j$ 个 $>k$ 的数,相当于 $\geq k+1$,所以我们把这些数先减去 $(k+1)$,剩下的就没有限制了(均为 $\geq 0$),就等同于 $$a_1'+a_2'+…+a_j'+a_{j+1}+…+a_n = m-j(k+1)$$
其中每一项 $\geq 0$ 的方案数,那也就是 $C_{n+m-j(k+1)-1}^{n-1}$
另外如果 $j$ 是偶数,就是加号,否则为减号,所以右手边的第 $j$ 项等于:
$$(-1)^j * C_n^j * C_{n+m-j(k+1)-1}^{n-1}$$
• 最后提一下,这个:
$$a_1+a_2+…+a_{n-m+1} = m,~~ a_i \in [0,k]$$
也可以用生成函数做,相当于 $f(x) = 1+x+x^2+…+x^k$,求 $f(x)^{n-m+1}$ 的第 $m$ 项系数,多项式快速幂即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
ll f[maxn];
ll fac[maxn], inv_fac[maxn];
// C(a,b) = a! / b! / (a-b)!
ll C(ll a, ll b) {
if (b < 0 || a < b) return 0;
return fac[a] * inv_fac[b] % mod * inv_fac[a-b] % mod;
}
ll qpow(ll a, ll b) {
ll res = 1;
while (b) {
if (b & 1) {
res = res * a % mod;
}
a = a * a % mod;
b >>= 1;
}
return res;
}
// 计算最大连续 <= k 的情况数
ll cal(ll n, ll m, ll k) {
if (k > m || m > n) return 0;
if (k == 0) return (m == 0);
// n-m+1 个空里面 插 m 个球,限制为 [0,k]
// a_1 + a_2 + ... a_{n-m+1} = m, a_i in [0,k]
n = n - m + 1;
// a_1 + a_2 + ... a_{n} = m, a_i in [0,k]
ll ans = 0;
for (ll j = 0; j <= n; j++) {
ll res = C(n,p) * C(n+m-j*(k+1)-1, n-1);
if (p & 1) ans = (ans - res + mod) % mod;
else ans = (ans + res) % mod;
}
return ans;
}
ll n,m,k;
int main() {
cin >> n >> m >> k;
if (n-m+1 <= 0) {
cout << 0 << endl;
return 0;
}
fac[0] = inv_fac[0] = 1;
for (ll i = 1; i <= maxn-2; i++) {
fac[i] = fac[i-1] * i % mod;
}
inv_fac[maxn-2] = qpow(fac[maxn-2], mod-2);
for (ll i = maxn-3; i >= 1; i--) {
inv_fac[i] = inv_fac[i+1] * (i+1) % mod;
}
cout << (cal(n,m,k) - cal(n,m,k-1) + mod) % mod << endl;
}
例2 Atcoder ABC235G Gardens
题意
给定 $a$ 个苹果种子,$b$ 个香蕉种子,$c$ 个樱桃种子,同类型的种子之间没有区别。
有 $n$ 个花园(花园之间是有区别的),我们要满足以下条件:
- 每个花园至少种下一个种子。
- 对于每个花园,每一类的种子最多只能有一个。
- 不一定需要使用完所有种子。
求所有方案数?答案对 $998244353$ 取模。
其中,$1 \leq n \leq 5 \times 10^6, a,b,c \in [0,n]$。
题解
先膜jiangly的神仙讲解。
对于容斥的问题,一种常见的套路是 先去掉一个条件。
我们如果去掉第一个条件的话,我们会发现每一类的种子其实是独立的!
所以我们考虑苹果种子,我们可以枚举使用种子的数量 $i$,$i$ 的取值范围是 $i \in [0, \min \{n,a\}]$。
如果我们用了 $i$ 个苹果种子,那么方案数就有 $C_n^i$ 种。
那么对于苹果种子来说,总方案数就是:
$$\sum\limits_{i=0}^{\min \{n,a\}} C_n^i$$
有两种情况:
- 如果 $a \geq n$,总方案数就是 $\sum\limits_{i=0}^{n} C_n^i = 2^n$。
- 如果 $a < n$,总方案数就是 $\sum\limits_{i=0}^{a} C_n^i$。
其他两类种子一样,乘起来即可。
现在我们需要考虑上第一种条件了。
这个容斥跟上一题很像,因为这个 每个花园至少种一个种子 实际上就是 花园 $i$ 种子数 $\geq 1$ 的并集(从 $1$ 并到 $n$),所以方案数是
无限制 - 一个为空 + 两个为空 - 三个为空 ……
写成数学表达式就是:
$$\sum\limits_{j=0}^n \{(-1)^j * C_n^j * (\sum\limits_{i=0}^{\min \{n,a\}} C_n^i) * (\sum\limits_{i=0}^{\min \{n,b\}} C_n^i) * (\sum\limits_{i=0}^{\min \{n,c\}} C_n^i)\}$$
这里 $j$ 代表有多少个花园是空的。$C_n^j$ 就是 $n$ 个中选择 $j$ 个花园作为空花园。
不过还剩下一个问题,这看起来是个 $O(n^2)$ 的做法,我们需要快速计算
$$\sum\limits_{i=0}^{\min \{n,a\}} C_n^i$$
因为我们只需要考虑 $a < n$ 的情况,所以只要计算:
$$\sum\limits_{i=0}^{a} C_n^i$$
根据组合数的性质:
$$C_n^m = C_{n-1}^{m-1} + C_{n-1}^m$$
那么上式就可以化简为:
$$\sum\limits_{i=0}^{a} C_n^i = \sum\limits_{i=0}^{a} (C_{n-1}^{i-1} + C_{n-1}^i) = \sum\limits_{i=0}^{a-1}C_{n-1}^i + \sum\limits_{i=0}^{a} C_{n-1}^i = 2 * \sum\limits_{i=0}^{a} C_{n-1}^i - C_{n-1}^a$$
所以我们只要算出 $\sum\limits_{i=0}^{a} C_{n-1}^i$,我们可以在 $O(1)$ 时间内算出 $\sum\limits_{i=0}^{a} C_{n}^i$。
所以 $j$ 从 $n$ 往 $0$ 枚举即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e6+5;
template<class T>
T qpow(T a, int b) {
T res = 1;
while (b) {
if (b & 1) res *= a;
a *= a;
b >>= 1;
}
return res;
}
int norm(int x) {
if (x < 0) {
x += mod;
}
if (x >= mod) {
x -= mod;
}
return x;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(mod - x));
}
Z inv() const {
assert(x != 0);
return qpow(*this, mod - 2);
}
Z &operator*=(const Z &rhs) {
x = (ll)(x) * rhs.x % mod;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
};
Z fac[maxn], inv_fac[maxn], P[maxn], pre[3];
Z C(int n, int m) {
return fac[n] * inv_fac[n-m] * inv_fac[m];
}
int n, a, b, c;
int main() {
cin >> n >> a >> b >> c;
fac[0] = inv_fac[0] = P[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = fac[i-1] * i, P[i] = P[i-1] * 2;
inv_fac[n] = qpow(fac[n], mod-2);
for (int i = n-1; i >= 1; i--) inv_fac[i] = inv_fac[i+1] * (i+1);
Z ans = 0;
for (int j = n; j >= 0; j--) {
int flag = (j & 1) ? -1 : 1;
Z res = flag;
res *= C(n, j);
Z asum = (a >= n-j) ? (P[n-j]) : (pre[0] * 2 - C(n-j-1, a));
Z bsum = (b >= n-j) ? (P[n-j]) : (pre[1] * 2 - C(n-j-1, b));
Z csum = (c >= n-j) ? (P[n-j]) : (pre[2] * 2 - C(n-j-1, c));
res *= asum * bsum * csum;
pre[0] = asum, pre[1] = bsum, pre[2] = csum;
ans += res;
}
cout << ans.val() << endl;
}
