二维差分
Contents
介绍
一维差分可以用于解决以下问题:
给定一系列的区间加/减操作,最后询问整个数组的元素。
那么二维差分就可以解决:
给定一系列的矩阵加/减操作,最后询问整个矩阵中的元素。
二维差分原理
我们知道,二维前缀和的计算方式是:
$$sum[x][y] = sum[x-1][y] + sum[x][y-1] - sum[x-1][y-1]$$
所以我们思考,对于差分数组 $d[x][y]$,如果我们要给一个矩阵
$$[x_1,y_1][x_2,y_2]$$
全部加 $1$,即左上角为 $(x_1,y_1)$,右下角为 $(x_2,y_2)$ 的矩阵全部加 $1$,应该怎么处理?
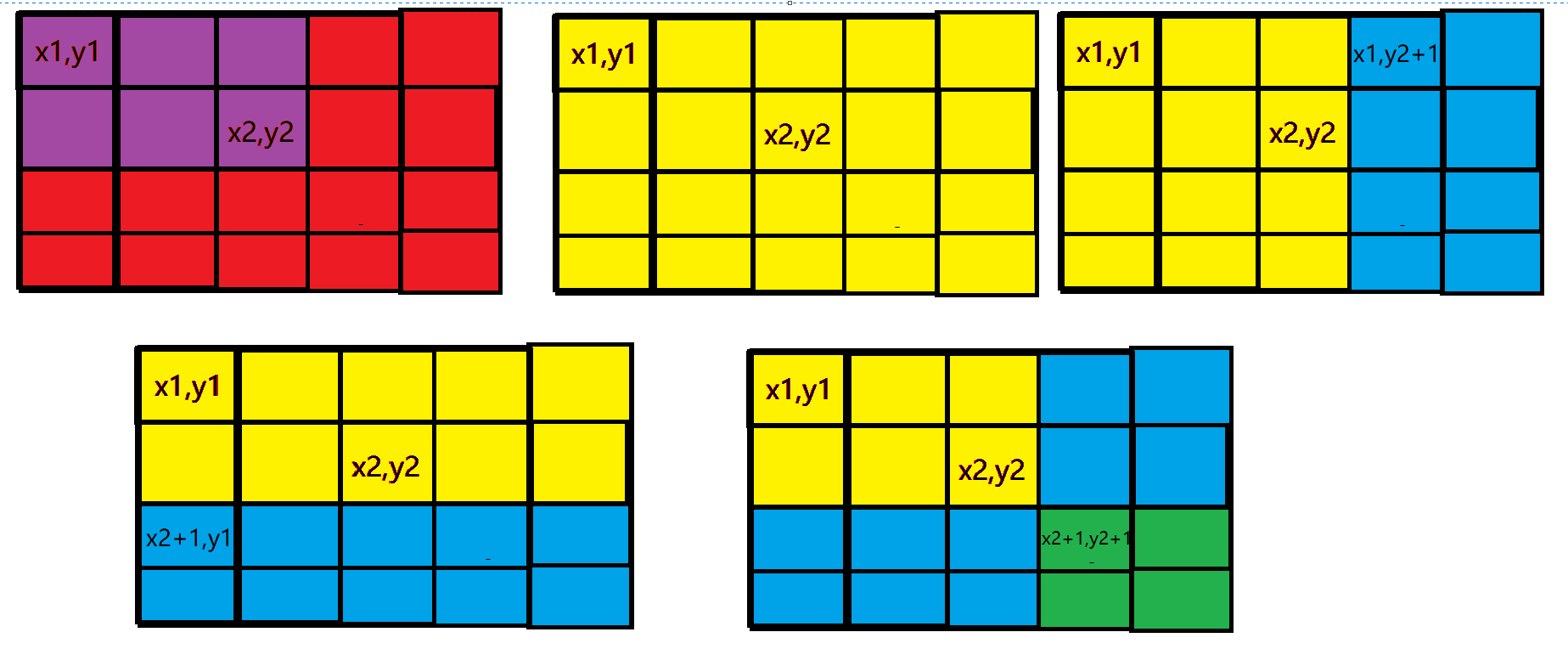
注意到如果我们进行二维前缀和的话,修改一个差分数组 $d[x][y]$ 影响到的是 $(x,y)$ 右下方的所有元素的值。
我们想要的是 紫色部分 全部加 $1$。
那么如果我们让 $d[x_1][y_1]$ 加 $1$,那么影响到的是所有的 紫色加红色 部分。
于是,我们可以通过让 $d[x_1][y_2+1]$ 和 $d[x_2+1][y_1]$ 全部减去 $1$ 来消除红色部分。
然而 绿色部分 被减去了两次,所以我们再给 $d[x_2+1][y_2+1]$ 加上 $1$。
在所有的操作结束后,使用 二维前缀和 的方式来获得矩阵值即可。
void update(ll arr[][maxn], int xl, int xr, int yl, int yr, ll val) {
arr[xl][yl] += val;
arr[xr+1][yr+1] += val;
arr[xl][yr+1] -= val;
arr[xr+1][yl] -= val;
}
例题
例1 2018ICPC焦作J题 Carpets Removal
题意
给定 $m\times m$ 的一个矩阵,并且给定 $n$ 个地毯(每个地毯是一个矩形)。
我们需要移除 恰好两个地毯,使得 没有被地毯覆盖到的格子数量 最大。
输出这个最大值。
其中,$3 \leq n \leq 3 \times 10^5, 1 \leq m \leq 1500$。
题解
首先,我们可以利用二维差分,求出每个格子的覆盖次数。
我们知道,如果一个格子被覆盖的次数 $\geq 3$,那么可以直接忽略。
所以我们只考虑覆盖次数为 $1$ 或者 $2$ 的格子。
我们分开讨论。
对于覆盖次数为 $1$ 的格子,我们可以把它们单独拿出来,在一个全部为 $0$ 的矩阵中,然后把这些 $1$ 放进去。
这样我们可以得出每个地毯所覆盖的 $1$ 的数量。
我们设第 $i$ 个地毯覆盖的 $1$ 的数量为 $a_i$。
对于覆盖次数为 $2$ 的格子,假设覆盖它的地毯分别为 $i,j$,那么我们设 $b_{ij}$ 为地毯 $i,j$ 共同覆盖的,覆盖次数为 $2$ 的格子数量。
所以最后的最大值就是
$$\max\limits_{(i,j)}\{a_i+a_j+b_{ij}\}$$
$a_i$ 我们可以求出,但是 $b_{ij}$ 呢?
假设我们知道对于每个覆盖次数为 $2$ 的格子,覆盖它的两个地毯 index 为 $i,j$,那么这个 $b_{ij}$ 就可以求出。
我们利用 二维差分 来记录这样的信息!
除了我们维护的 cnt[][] 来代表覆盖次数以外,我们再额外维护两个信息:
sum[][]:如果 $(i,j)$ 被地毯 $x$ 覆盖,那么它的值会被加上 $x$。sum2[][]:如果 $(i,j)$ 被地毯 $x$ 覆盖,那么它的值会被加上 $x^2$。
对于 cnt[i][j] == 1 的格子,我们只要看一下 sum[i][j],就可以知道它是被哪个地毯覆盖的了。
对于 cnt[i][j] == 2 的格子,我们可以知道它被两个地毯 $x,y$ 所覆盖,并且我们知道 $(x+y)$ 与 $(x^2+y^2)$ 的值。
那么我们只要利用 $$2(x^2+y^2) - (x+y)^2 = x^2 + y^2 - 2xy = (x-y)^2$$
就可以求出 $|x-y|$ 的值,那么用 $\frac{(x+y) \pm |x-y|}{2}$ 即可求出 $x,y$。
最后要注意,有可能有 $b_{ij} = 0$,所以我们还需要让答案再考虑一下
$$\max\limits_{(i,j)}\{a_i+a_j\}$$
这个只要在 $a_i$ 中找到前 $2$ 大的加起来就可以了。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1515;
const int maxm = 3e5+50;
ll n,m;
ll cnt[maxn][maxn];
ll sum1[maxn][maxn], sum2[maxn][maxn];
void update(ll arr[][maxn], int xl, int xr, int yl, int yr, ll val) {
arr[xl][yl] += val;
arr[xr+1][yr+1] += val;
arr[xl][yr+1] -= val;
arr[xr+1][yl] -= val;
}
ll one[maxm];
void solve() {
cin >> n >> m;
for (ll i = 1; i <= n; i++) {
int xl,xr,yl,yr; cin >> xl >> xr >> yl >> yr;
update(cnt, xl, xr, yl, yr, 1);
update(sum1, xl, xr, yl, yr, i);
update(sum2, xl, xr, yl, yr, i*i);
}
map<pii,int> mp;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= m; j++) {
cnt[i][j] += cnt[i][j-1] + cnt[i-1][j] - cnt[i-1][j-1];
sum1[i][j] += sum1[i][j-1] + sum1[i-1][j] - sum1[i-1][j-1];
sum2[i][j] += sum2[i][j-1] + sum2[i-1][j] - sum2[i-1][j-1];
if (cnt[i][j] == 1) {
ll x = sum1[i][j];
one[x]++;
} else if (cnt[i][j] == 2) {
ll d = sqrt(2LL * sum2[i][j] - sum1[i][j] * sum1[i][j]); // d = abs(x-y)
ll x = (sum1[i][j] + d) / 2, y = (sum1[i][j] - d) / 2;
if (x > y) swap(x, y);
mp[{x,y}]++;
}
}
}
ll ans = 0;
for (auto p : mp) {
int x = p.first.first, y = p.first.second;
ll a = p.second;
ans = max(ans, one[x] + one[y] + a);
}
ll m1 = 0, m2 = 0;
for (int i = 1; i <= n; i++) {
m1 = max(m1, one[i]);
if (m1 > m2) {
swap(m1, m2);
}
}
ans = max(ans, m1 + m2);
ans = -ans;
LOG(ans);
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= m; j++) {
ans += (cnt[i][j] > 0);
}
}
cout << ans << "\n";
for (int i = 0; i <= m+2; i++) {
for (int j = 0; j <= m+2; j++) {
cnt[i][j] = sum1[i][j] = sum2[i][j] = 0;
}
}
fill(one, one+n+2, 0);
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
