介绍

Treap是一个自平衡的 BST (Binary Search Tree)。与普通BST不同的在于，每个节点会有一个随机的优先级 (priority/rank)，在不破坏 BST 的性质的情况下，保证了每一个子树根据 优先级 形成一个最小堆。

这样，Treap的所有操作均为 $O(\log n)$。

Treap支持的操作有：

  1. 插入
  2. 删除
  3. 根据值查询排名
  4. 根据排名查询值
  5. 查询第一个值比 val 小的节点
  6. 查询第一个值比 val 大的节点

结构/操作

需要同时维护 BST 和 最小堆的性质，我们利用旋转来维护这个性质。

img

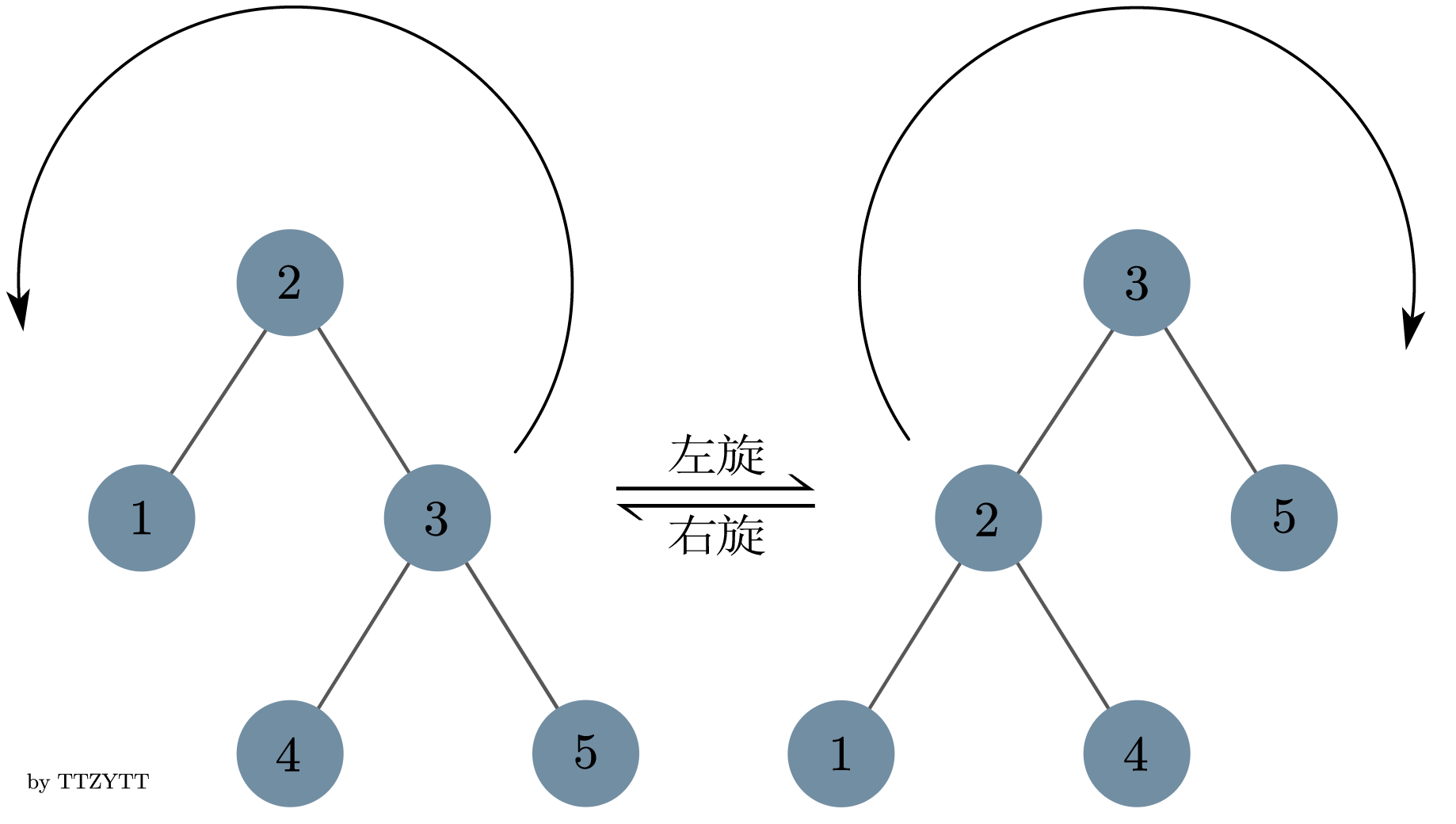
所以为了维护最小堆性质，只要对于一个节点 $u$，在插入节点后，判断插入左/右的 priority 是否比它小，如果是，将最小priority的那个旋转上来。

性质

  1. Treap 相当于将所有值赋上随机的 priority 后，按照priority从小到大的顺序插入进一个普通的 BST 中。

  2. $\forall i \neq k, i ↑ k \iff p_i = \min(\{p_i, p_{i+1}, … p_k\})$

    这里 $i ↑ k$ 的意思是 $i$ 是 $k$ 的祖先。我们这里假设 $\forall i$，第 $i$ 个节点有整个 treap 中第 $i$ 大的val，$p_i$ 代表了 $i$ 的 priority（这里 WLOG 假设了 $i<k$）。

    证明：

    考虑当前子树中：

    Case1: $i$ 为 $k$ 的祖先，这很明显说明 $i$ 在这个子树内的priority是最小的，反之亦然。

    Case2: $j$ 为 $k$ 的祖先，$j \neq i, j \neq k$，并且 $i,k$ 在不同的子树中，那么条件不成立。

    Case3: $j$ 为 $k$ 的祖先，$j \neq i, j \neq k$，并且 $i,k$ 在相同的子树中，那么则可以递归解决。

  3. $\Pr(i ↑ k) = \frac{1}{|i-k|+1}, i \neq k$

    证明：由性质 $2$，可以得知因为所有的priority均为随机，所以 $p_i$ 成为最小值的概率为 $\frac{1}{|i-k|+1}$

  4. $E[depth(k)] = \sum\limits_{i=1}^n \Pr(i ↑ k) = O(\log n)$。

    这也解释了为什么 Treap 的复杂度是 $O(\log n)$。