KMP - tom0727's blog

介绍

KMP算法能在 $O(n)$ 的时间内，求出一个字符串的每个前缀的最长 border 长度。

利用 border 的性质，也可以在 $O(n)$ 的时间内，求出一个字符串 $t$ 在文本串 $s$ 中出现的所有位置。

一个字符串 $s$ 的 border 是指 $s$ 的一个长度为 $j$ 的前缀，使得长度为 $j$ 的后缀与这个前缀相等，其中 $j<n$。

形式化的说，若 $s$ 任何border的长度为 $j$，那么满足：

s[1 ... j] = s[n-j+1 ... n]

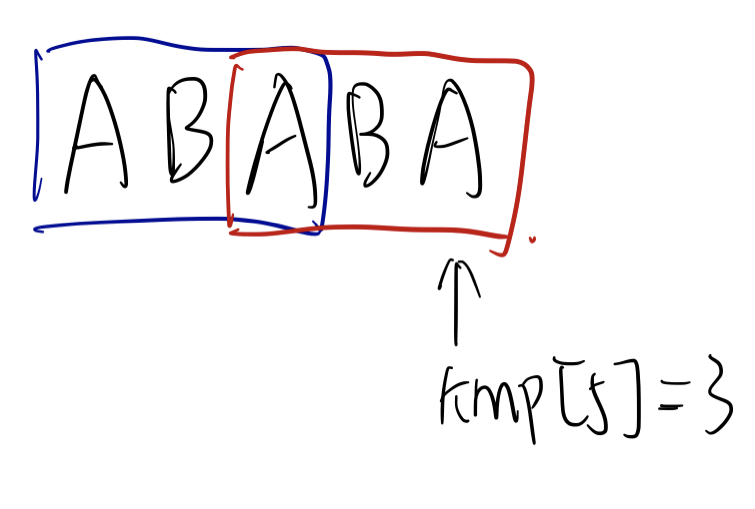
如图，这个字符串的最长 border 长度为 $3$。

kmp 算法做的事情就是，对于每个 $i$，求出 kmp[i]，其中 kmp[i] 的值代表 $s[1…i]$ 的最长的border长度。

那么怎么求 kmp[] 数组呢？

char s[maxn];
int kmp[maxn];

int main() {
    int n; scanf("%d",&n);
    scanf("%s", s+1);

    int j = 0;
    for (int i = 2; i <= n; i++) {
        while (j > 0 && s[i] != s[j+1]) j = kmp[j];
        if (s[i] == s[j+1]) j++;
        kmp[i] = j;
    }
}

基本思路是维护两个指针 $i,j$，$i$ 表示后缀，$j$ 表示前缀，在 $s_i,s_j$ 匹配时 $i,j$ 向前走一格，如果不匹配，那么 $j$ 跳回前一个更小的 border 处，这样保证了在任何时刻都有 s[1 ... j] = s[n-j+1 ... n]，然后继续判断 $s_i,s_j$ 是否匹配。

性质

一个字符串有很多个 border，但是所有较小的border一定是 最大border的border。

例如 ABABA 有两个border，一个是 ABA，一个是 A，可以发现 A 是 ABA 的一个border。

应用

查找子串

查找 $t$ 在 $s$ 内出现的所有位置，只要先对 $t$ 跑一次kmp，处理出 $t$ 上的 kmp 数组，然后在匹配的过程中，把 $i$ 指针放在 $s$ 上，$j$ 指针放在 $t$ 上，当 $j = n_2$ 时说明找到一个匹配，那么就让 $j = kmp[j]$ 继续匹配。

代码

void findstr(string& s, string t) {
    int n = s.size(), m = t.size();
    vector<int> kmp(m+1, 0);
    int j = 0;
    for (int i = 2; i <= m; i++) {
        while (j > 0 && t[i-1] != t[j]) j = kmp[j];
        if (t[i-1] == t[j]) j++;
        kmp[i] = j;
    }
    j = 0;
    for (int i = 1; i <= n; i++) {
        while (j > 0 && s[i-1] != t[j]) j = kmp[j];
        if (s[i-1] == t[j]) j++;
        if (j == m) {
            printf("%d\n",i-j+1);
            j = kmp[j];
        }
    }
}

周期/循环节

对于长度为 $n$ 的字符串 $s$，若 $p \in [1, n]$ 满足

$$s[i] = s[i+p], \forall i \in [1, n-p]$$

说明 $p$ 是 $s$ 的周期。

满足条件的 $p$ 可能有很多，但所有的 $p$ 一定满足：

$$p_i = n - f^i(n)$$

这里 $f^1(n) = kmp[n], f^{i}(n) = kmp[f^{i-1}(n)]$，$f^{i}(n)$ 代表了 $s$ 的所有border的长度。

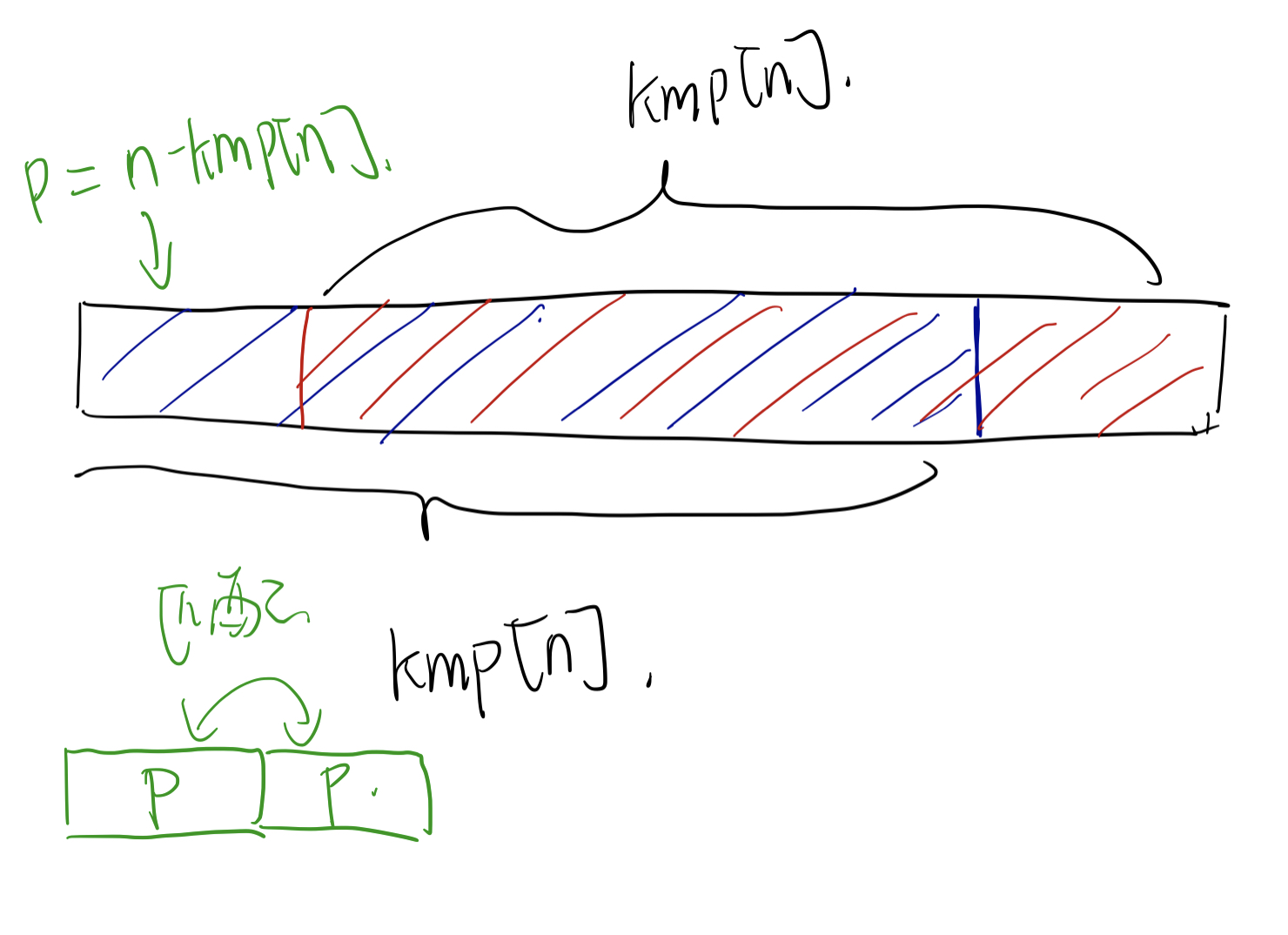
如上图，可以看出 s[1 ... p] == s[p+1 ... 2p]，后面的也可以由此推出，所以 $p$ 是一个周期。

循环节的定义：如果一个字符串 $s$ 可以表达为 $s = (X)(X)…(X)$ 这种形式说明 $(X)$ 是一个循环节。

例如 s = "abababab"，那么 ab 是循环节，abab 也是循环节。

一个字符串拥有循环节，并且循环节长度为 $p$ 当且仅当：

$p$ 是一个周期。
n % p == 0。

换而言之，只要判断 p = n - kmp[n], n % p == 0 是否成立即可。

同周期，循环节可能有很多个，寻找的方式跟周期一样，额外判断一下 n % p == 0 是否成立即可。

• 最小循环节的长度就是 $n - kmp[n]$。

最小表示法

虽然和 KMP 并没有必然联系，但思想上可能有些相同。

定义一个字符串 $s$ 和另外一个字符串 $t$ 循环同构 (cyclic shift)，当且仅当

$$\exists i \in [1,n], s[i…n] + s[1…i-1] = t$$

Equivalently，有：

$t$ 与 $s$ 循环同构。
$t$ 可以用 $s$ 的位置为 $i$ 的后缀，加上位置为 $i$ 的前缀组成。
$t$ 是 $s+s$ 中的一个 substring（注意前提是 $|s| = |t|$）。

• 注意到由于性质 $3$，也可以用 KMP 在 $O(n)$ 判断两个字符串是否为循环同构。

最小表示法可以在 $O(n)$ 时间内求出一个字符串 字典序最小 的循环同构。

方法是维护两个指针 $i,j$，讨论三种情况：

Case1: $s_i < s_j$：说明 $j$ 不可能为最小表示的起点，所以 j++;。

Case2: $s_i > s_j$：说明 $i$ 不可能为最小表示的起点，所以 i++;。

Case3: $s_i = s_j$：说明需要接着往后看，所以用另外一个值 $k$，让 $k$ 从 $0$ 开始加，直到 $s_{i+k} \neq s_{j+k}$。

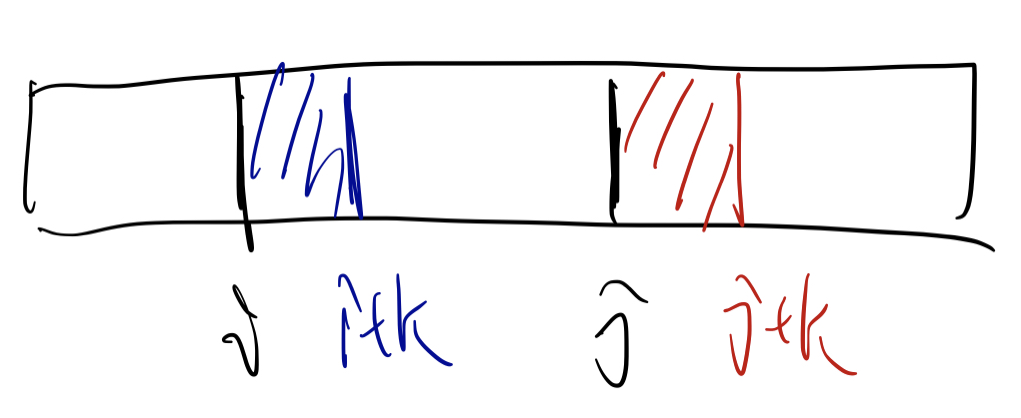
Case3.1: 如果 $s_{i+k} < s_{j+k}$：说明任何 $j’ \in [j, j+k]$ 不可能满足条件，因为如果满足了，必然有对应相同位置的 $i'$ 更好。所以令 j = j+k+1;。

Case3.2: 如果 $s_{i+k} > s_{j+k}$：说明任何 $i’ \in [i, i+k]$ 不可能满足条件，因为如果满足了，必然有对应相同位置的 $j'$ 更好。所以令 i = i+k+1;。

代码

// 输出 s 的最小表示法
string min_cyc(string s) {
    int n = s.size();
    int i = 0, j = 1, k = 0;
    while (i < n && j < n && k < n) {
        char a = s[(i+k) % n], b = s[(j+k) % n];
        if (a == b) k++;
        else {
            if (a < b) j = j+k+1;
            if (a > b) i = i+k+1;
            if (i == j) i++;  // 如果重合就后移 
            k = 0;
        }
    }
    i = min(i, j);  // 保证是一个合法位置 (结束时i,j很有可能有一个非法)
    return s.substr(i, n-i) + s.substr(0, i);
}

失配树

例题

例1 HDU3746 Cyclic Nacklace

题意

给定一个字符串 $s$，求需要在它的尾部加最少几个字符，使得它拥有循环节？

其中，$n \leq 10^5$。

题解

根据循环节的定义，先判断循环节是否存在，如果已经存在返回 0。

如果不存在，那么只需要求出最小周期 $p$，然后判断还差多少个字符能够形成循环节即可，这个循环节的长度就是最小周期 $p$。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
char s[maxn];
int kmp[maxn];
int main() {
    int T; cin >> T;
    while (T--) {
        scanf("%s", s+1);
        int n = strlen(s+1);
        int j = 0;
        for (int i = 2; i <= n; i++) {
            while (j > 0 && s[i] != s[j+1]) j = kmp[j];
            if (s[i] == s[j+1]) j++;
            kmp[i] = j;
        }
        int len = n - kmp[n];
        if (len == n) {
            cout << n << endl;
        } else {
            if (n % len == 0) {
                cout << 0 << endl;
            } else {
                cout << len - n % len << endl;
            }
        }
    }
}

例2 POI2006 OKR-Periods of Words

题意

给定一个字符串 $s$，对于这个字符串的每一个前缀 $s_i = s[1…i]$，找出一个最大的 $Q$ 使得：

$Q$ 是 $s_i$ 的前缀，且 $Q \neq s_i$。
$s_i$ 是 $Q+Q$ 的前缀（可以相等）。

求出对于每个 $i$，这样 $Q$ 的最大长度之和。（如果不存在的话就是 $0$）

其中，$n \leq 10^6$。

题解

我们会发现，如果 $Q$ 不存在的话，说明是类似于 "ABCD" 这种的字符串，这种字符串代表 $kmp[n] = 0$。否则类似于 "ABCA" 这种，Q = "ABC" 就满足要求。

简单推导可以发现，只要找到 $s_i$ 的最小 border 长度 $j$，然后 $Q = i-j$。

问题在于 kmp[] 维护的是最大border长度，最小border怎么办？

注意到最小border可以通过最大border一直往前跳获得，所以我们在初始处理 kmp 数组时仍然保留最大border。

然后枚举第二次，从 $1$ 枚举到 $n$，每次枚举完都让 kmp[i] 维护的是最小 border 的长度，这样后面的在往前跳的时候只用跳一次了。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
char s[maxn];
int kmp[maxn];

int main() {
    int n; scanf("%d",&n);
    scanf("%s", s+1);

    int j = 0;
    for (int i = 2; i <= n; i++) {
        while (j > 0 && s[i] != s[j+1]) j = kmp[j];
        if (s[i] == s[j+1]) j++;
        kmp[i] = j;
    }

    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        while (kmp[kmp[i]] > 0) kmp[i] = kmp[kmp[i]];  // 这里处理了最小border
        if (kmp[i]) {
            ans += (i-kmp[i]);
        }
    }
    cout << ans << endl;
}

例3 HDU3336 Count the string

题意

给定一个字符串 $s$，对于它的每一个前缀 $s_i$，找到 $s_i$ 在 $s$ 内出现的次数，输出所有前缀的出现次数之和。

其中，$n \leq 2 \times 10^5$，答案对 $10007$ 取模。

Follow Up: 如果给定另外一个字符串 $t$，对于 $s$ 的每一个前缀 $s_i$，求 $s_i$ 在 $t$ 内出现的次数？

题解

KMP + DP。

我们设 $dp[i]$ 为：长度为 $i$ 的前缀的出现次数。

我们可以发现，一个前缀 $s_k$ 如果出现在了 $s$ 内，那么它出现的一个位置的右端点为 $j$ 的话，必然有: $s_k$ 是前缀 $s_j$ 的一个border。

于是我们发现，如果 $i$ 的kmp值 $kmp[i] = j$，那么一个最大的前缀 $s_j$ 出现了并且以 $i$ 作为右端点，也就是说 s[1 ... j] = s[i-j+1 ... i]。

那么更小的前缀呢？我们可以先把 $dp[i]$ 加到 $dp[j]$ 上，更小的前缀留到之后处理 $s_j$ 的时候再一起考虑它们。

所以我们从后往前处理。

int ans = 0;
for (int i = n; i >= 1; i--) {
    dp[i]++;
    dp[kmp[i]] += dp[i];
    ans += dp[i];
}

Follow Up:

创造一个新的string s + "#" + t。

"#" 的目的是让整个串的 border 不会穿过 "#"。

仍然设 $dp[i]$ 为：长度为 $i$ 的前缀的出现次数。然后对整个串跑一次 kmp。

不同的是，我们这次分开处理。

先处理 $t$ 的部分，对于 $t$ 内的所有index $i$，给所有的 dp[kmp[i]]++;。

接着处理 $s$ 即可，处理方法和之前完全一样。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
char s[maxn];
int kmp[maxn];
int dp[maxn];

int main() {
    int T;
    scanf("%d",&T);
    while (T--) {
        int n; scanf("%d",&n);
        scanf("%s", s+1);

        int j = 0;
        for (int i = 2; i <= n; i++) {
            while (j > 0 && s[i] != s[j+1]) j = kmp[j];
            if (s[i] == s[j+1]) j++;
            kmp[i] = j;
        }

        int ans = 0;
        for (int i = n; i >= 1; i--) {
            dp[i]++;
            (dp[kmp[i]] += dp[i]) %= 10007;
            (ans += dp[i]) %= 10007;
        }

        printf("%d\n", ans);
        fill(kmp, kmp+n+1, 0);
        fill(dp, dp+n+1, 0);
    }
}

Follow Up 代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
char s[maxn];
int kmp[maxn];
int dp[maxn];

int main() {
    int T;
    scanf("%d",&T);
    while (T--) {
        int n, m; scanf("%d%d",&n,&m);
        scanf("%s", s+1);  // 输入 s
        s[n+1] = '#';
        scanf("%s", s+n+2);  // 输入 t

        int j = 0;
        for (int i = 2; i <= n+m+1; i++) {
            while (j > 0 && s[i] != s[j+1]) j = kmp[j];
            if (s[i] == s[j+1]) j++;
            kmp[i] = j;
        }

        int ans = 0;
        for (int i = n+m+1; i >= n+2; i--) {
            if (kmp[i] > 0) dp[kmp[i]]++;
        }
        for (int i = n; i >= 1; i--) {
            if (kmp[i] > 0) dp[kmp[i]] += dp[i];
            ans += dp[i];
        }

        printf("%d\n", ans);
        fill(kmp, kmp+n+1, 0);
        fill(dp, dp+n+1, 0);
    }
}

例4 HDU2609 How many

题意

给定 $n$ 个长度相同的字符串，问有多少个本质不同的字符串？

$s,t$ 本质不同当且仅当 $s,t$ 不互为循环同构。

其中，$n \leq 10000$，每个字符串长度 $\leq 100$。

题解

求出每个字符串的最小表示法，去一下重即可。（代码都不用放了）。

例5 CF808G Anthem of Berland

题意

给定一个包含小写字母和 '?' 的字符串 $s$，和一个仅包含小写字母的字符串 $t$，求如何替换 $s$ 中的 '?' 为小写字母，使得 $t$ 在 $s$ 中出现的次数最多？

其中，$|s|, |t| \leq 10^5, |s| * |t| \leq 10^7$。

题解

KMP + DP。

注意到 $|s| * |t| \leq 10^7$。

思考一个 dp 的做法：$dp[i][j]$ 代表匹配到了 $s$ 的第 $i$ 位，此时尝试匹配 $s_i$ 和 $t_{j+1}$（之所以是 $j+1$ 是因为 KMP 的写法），dp数组的值代表此时 $t$ 出现的次数。

如果匹配成功，那么有：

$$dp[i+1][j+1] = dp[i][j]$$

特别的，当 $j+1 = m$ 时，出现次数加 $1$。那么按照 kmp 的做法，在匹配完成后，需要跳回 kmp[m] 的位置继续匹配。

所以在 $j+1 = m$ 时有：

$$dp[i+1][kmp[m]] = dp[i][j] + 1$$

如果匹配失败，那么就按照 KMP 的失配规则，$j$ 一直往前跳，直到 $s_i = t_{j+1}$。

以上讨论都基于没有 ? 的情况，有 ? 怎么办呢？

我们不能简单的说 '?' 就默认为匹配成功，可能存在一种情况使得 '?' 换成其他的字符更好，比如 s = "a?bc", t = "abc"。

既然总共就只有小写字母，不妨枚举 ? 的所有可能性，然后分别进行转移。

最后注意到复杂度有点爆炸，每次枚举 '?' 的值时 kmp 都要暴力往前跳。

不妨预处理一个 nxt[][] 数组，其中 nxt[c][j] 代表在 $s$ 的一个 '?' 替换成字符 $c$ 时，若此时正在匹配 $t_{j+1}$，那么 KMP 应该让它跳回什么地方？

其实这就是一个最小 border 问题，利用例 $2$ 的做法即可，这里只是加了一个枚举 $c$ 而已。

最终复杂度 $O(26 nm)$。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;

char s[maxn], t[maxn];
int kmp[maxn];
int nxt[26][maxn];
int main() {
    scanf("%s", s+1);
    scanf("%s", t+1);
    int n = strlen(s+1), m = strlen(t+1);
    vector<vector<int>> dp(n+2, vector<int>(m+2, -1e9));

    int j = 0;
    for (int i = 2; i <= m; i++) {
        while (j > 0 && t[i] != t[j+1]) j = kmp[j];
        if (t[i] == t[j+1]) j++;
        kmp[i] = j;
    }

    for (int i = 1; i <= n; i++) dp[i][0] = 0;
    for (int cc = 0; cc < 26; cc++) {  // 枚举 ? 替换成的字符
        char c = (char)(cc + 'a');
        for (int j = 0; j <= m; j++) {
            if (c == t[j+1]) nxt[cc][j] = j+1;  // 匹配成功则不需要跳
            else {
                nxt[cc][j] = nxt[cc][kmp[j]];  // 最小 border
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++){
            if (dp[i][j] == -1e9) continue;

            for (char c = 'a'; c <= 'z'; c++) {
                int nj = j, val = 0;
                if (s[i] != '?' && s[i] != c) continue;
                nj = nxt[c-'a'][j];
                // if (c == t[nj+1]) nj++;
                // else {
                //     while (nj > 0 && c != t[nj+1]) {
                //         nj = kmp[nj];
                //     }
                //     if(c == t[nj+1]) nj++;
                // }
                if (nj == m) {  // 匹配成功！往回跳一次
                    nj = kmp[nj];
                    val = 1;
                }
                dp[i+1][nj] = max(dp[i+1][nj], dp[i][j] + val);
            }
        }
    }

    int ans = 0;
    for (int i = 1; i <= n+1; i++) {  // 注意是 i 往 i+1 转移所以要在 n+1 取答案
        for (int j = 0; j <= m; j++) ans = max(ans, dp[i][j]);
    }
    cout << ans << endl;
}