线性规划 - tom0727's blog

介绍

线性规划问题一般表示为如下：

给定 $c_j, a_{ij}, b_i$，求 $x$ 的值使得

$$\max_x \sum_{j=1}^d c_jx_j$$

其中

$$\sum_{j=1}^d a_{ij} x_j \leq b_i, \forall i = 1…n$$ $$x_j \geq 0, \forall j = 1…d$$

等价的，可以把上式写作：

$$\max_x ~ c \cdot x$$

其中

$$Ax \leq b$$ $$x \geq 0$$

有 $c \in 1 \times d, A \in n \times d, x \in d \times 1, b \in n \times 1$。

我们称原问题为 Primary Problem, 对偶问题为 Dual Problem, 解决 Primary Problem 和解决 Dual Problem 是等价的。

按照上面定义的问题作为 Primary Problem，那么 Dual Problem 的形式可以写作：

$$\min_y y \cdot b$$

其中，

$$yA \geq c$$ $$y \geq 0$$

有 $y \in 1 \times n, b \in n \times 1, A \in n \times d, c \in 1 \times d$。

原问题：

给定一个二分图，边上有边权 $w_j$，找到一组匹配，使得匹配中的边权和最大。

我们定义 $n$ 为二分图中点的数量之和，$m$ 为边的数量。

定义一个系数矩阵 $A$

其中 $A_{i,j} = 1$ 当且仅当第 $i$ 个点是第 $j$ 条边的其中一个端点。

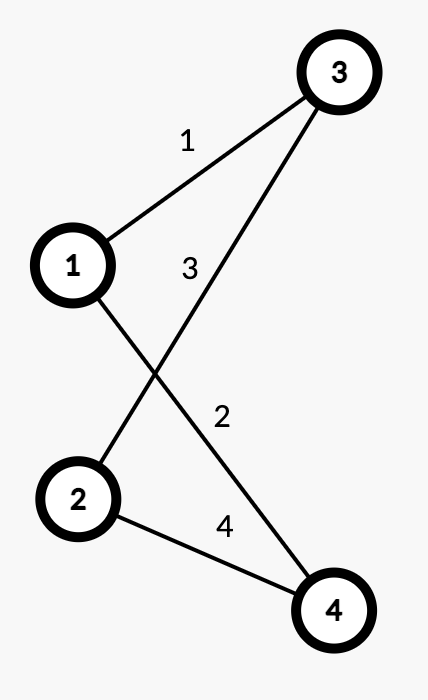
如图（注意边的数字代表着这是第几条边，边权在这张图里没写），系数矩阵为

$$A=\begin{bmatrix} 1 & 1 & 0 & 0 \\
0 & 0 & 1 & 1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1 \\
\end{bmatrix} $$

而 $x$ 就代表了 $m$ 条边，$x_j = 1$ 代表第 $j$ 条边在匹配内，$x_j = 0$ 代表不在。 $$b = \begin{bmatrix} 1 \\
1 \\
1 \\
1 \\
\end{bmatrix}$$

代表了这是一个匹配的限制，即每个点所连的边中，至多有一个被选进匹配中。

这满足了 $Ax \leq b, x \geq 0$ 的限制。

接下来我们考虑对偶问题：

$$\min_y y \cdot b$$

其中，

$$yA \geq c$$ $$y \geq 0$$

由于 $x$ 代表了 $m$ 条边，所以 $y$ 就代表了 $n$ 个点。

$A$ 的意义不变，还是代表了二分图本身，而 $c \in 1 \times m$ 代表了对于 $m$ 条边的限制，限制每条边的值最多为 $c_j$，也就是原问题中的边权。

那这个值是什么呢？我们考虑 $y$ 的意义。

$y$ 可以看出是给每个点赋值（我们在这里称这个值为顶标），然后和 $A$ 乘起来代表一个节点 $i$ 的顶标会被贡献到所有的与 $i$ 相连的边 $j$ 上。

所以对偶问题就是 最小顶标和：

给每个节点赋一个值（顶标），使得每条边两个端点的顶标和 $\geq$ 边权，且所有节点的顶标和最小。