博弈论与SG函数

公平组合游戏

公平组合游戏 Impartial Combinatorial Game (ICG) 满足以下性质：

有 $2$ 名玩家。
$2$ 名玩家轮流操作，在一个游戏集合中选其中一个进行操作。
对于任意一个合法的局面，当前的决策与之前的操作无关。
无法操作者（操作集合为空）会输掉游戏。

Nim游戏

Nim游戏是一个经典的 ICG。

游戏规则如下：

地上有 $n$ 堆石子，每堆石子数量可能不同，两人轮流操作，每人每次可从任意一堆石子里取走任意多枚石子，可以取完，不能不取，无石子可取者输掉游戏，问是否存在先手必胜的策略。

结论：如果石子的数量为 $a_1,a_2,…a_n$，那么先手获胜 $\iff a_1 \oplus a_2 \oplus … \oplus a_n = 0$，否则后手获胜。

证明：对于等于 $0$ 的情况，进行任意一个操作都一定会让 XOR 的值变成非 $0$。对于非 $0$ 的情况，一定存在某一个操作使得 XOR 的值变成 $0$。

前者易证，对于后者：假设 $a_1 \oplus a_2 \oplus … \oplus a_n = k > 0$，考虑 $k$ 的最高位为 $1$，所以一定存在一个 $a_i$ 使得 $a_i$ 的这一位也是 $1$，并且一定有 $a_i \oplus k < a_i$。

博弈图和状态

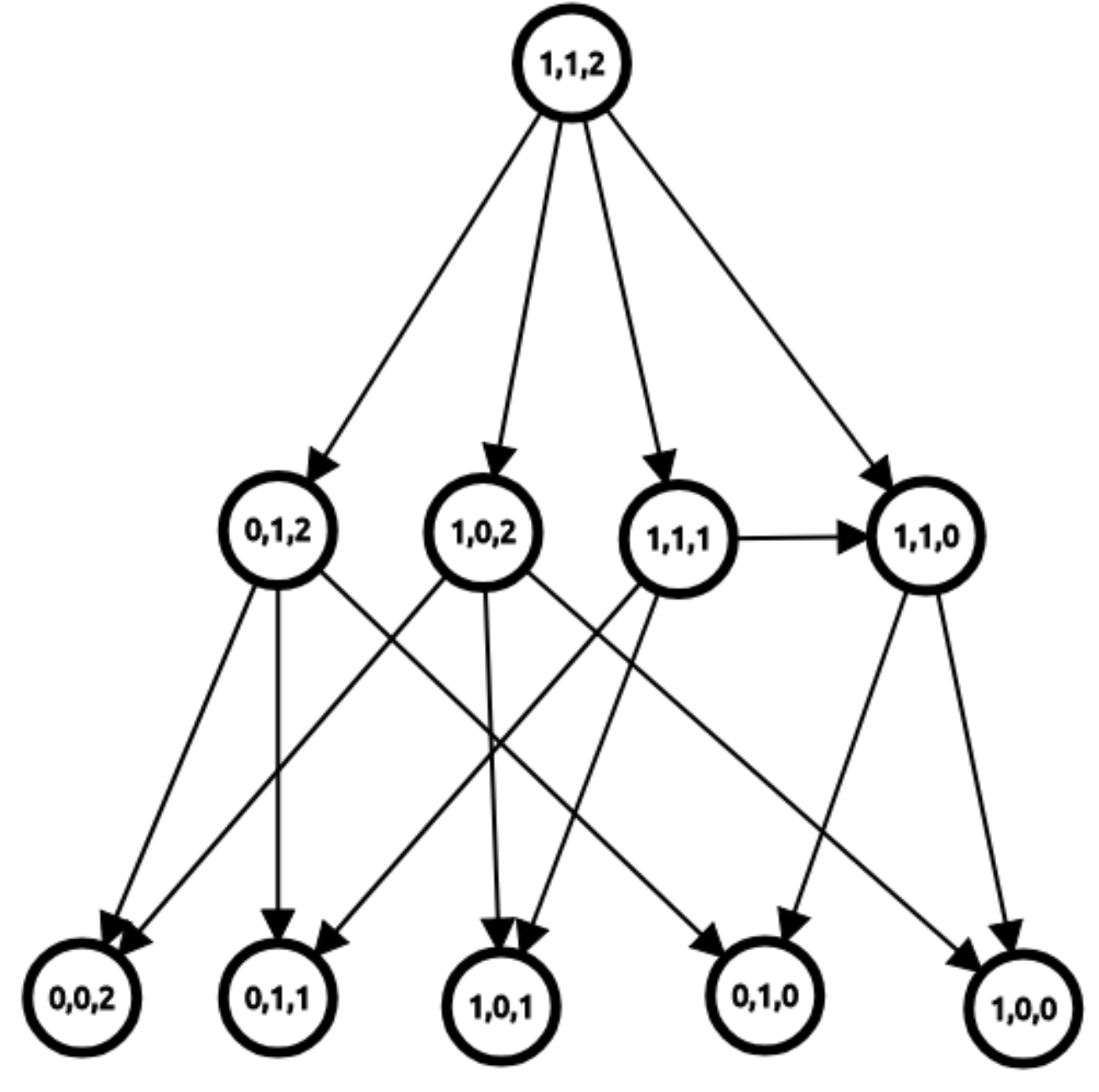
如果令节点 $(i,j,k)$ 表示局面为 $i,j,k$ 时的状态，就可以画出如上的博弈图。注意到这个博弈图是 DAG。

定义 必胜状态 为先手必胜的状态，必败状态 为先手必败的状态，有 $3$ 条定理：

没有后继状态（没有出边）的状态是必败状态。
一个状态是必胜状态 $\iff$ 它的后继状态存在至少 $1$ 个必败状态。
一个状态是必败状态 $\iff$ 它的所有后继状态均为必胜状态。

SG函数

我们定义 SG函数：$SG(x)$，其中 $x$ 是一个游戏状态，SG函数的值是一个非负整数。

如果没有后继状态 / 后继状态全部是必胜状态，那么 $SG(x) = 0$，表示必败状态。
如果后继状态中存在至少一个必败状态，那么 $SG(x) > 0$，表示必胜状态。

而 $SG$ 函数本身的定义如下：

对于状态 $x$ 和它的 $k$ 个后继状态 $y_1, y_2 … y_k$，定义

$$SG(x) = \text{mex}\{SG(y_1), SG(y_2), … , SG(y_k)\}$$

回忆一下 mex函数的定义：一个整数集合中，最小的没有出现的非负整数。

$$\text{mex}(S) = \min\{x | x \notin S, x \in N\}$$

根据这个定义，我们可以发现，对于当前状态 $x$，如果令 $a = SG(x)$，那么对于任意的 $b \in [0, a-1]$，一定存在某个后继状态 $y$ 使得 $b = SG(y)$。

这也解释了为什么 $SG(x) > 0$ 时代表必胜状态，而 $SG(x) = 0$ 代表必败状态。

• 因为 $SG(x)>0$ 就说明有一种后继状态 $y$ 使得 $SG(y) = 0$，而 $SG(x) = 0$ 说明不存在这样的 $SG(y) = 0$。

如果一个 ICG 包含了多个互相的独立状态 $x_1,x_2…,x_n$，那么这个 ICG 的 $SG$ 函数表示为：

$$SG(x_1) \oplus SG(x_2) \oplus … \oplus SG(x_n)$$

而类比一个状态的情况，可以得出：

$SG(x_1) \oplus SG(x_2) \oplus … \oplus SG(x_n) = 0$，表示必败状态。

$SG(x_1) \oplus SG(x_2) \oplus … \oplus SG(x_n) > 0$，表示必胜状态。

• 在 nim 游戏中，有 $SG(x) = x$，即当前状态有几个石子，SG函数就是几。

例题

例1 CF1823E. Removing Graph

题意

给定一个图，有 $n$ 个节点和 $n$ 条边，这个图是若干个联通分量组成的，每个联通分量一定是一个环。

现在 Alice 和 Bob 轮流对这个图进行一些操作，每次操作选择一个联通分量，然后删掉这个分量上的一些点和对应的边，这些点必须本身组成一个subgraph。

每次可以删 $[l,r]$ 个点。

求谁能赢？

其中，$n \leq 2 \times 10^5, 1 \leq l < r \leq n$。

题解

第一眼看起来像是 nim 游戏的变种（每次只能remove $[l,r]$ 个石头），如果是这样的话那么 sg(i) = (i % (l+r)) / l，但这个不太一样。

注意到将一个环的 subgraph remove掉以后，会断成两条链，这就不太一样了，所以我们只能打表找找规律。

我们设环和链的 SG 函数分别为 $A,B$，那么就有：

$$B_i = \text{mex} \{ B_j \text{ xor } B_k ~|~ j+k \in [i-r, i-l]\}$$

$$A_i = \text{mex} \{ B_j ~|~ j \in [i-r, i-l]\}$$

经过一些打表观察后，可以发现：

$A_i=0$ 当且仅当 $i \geq l+r$。
$A_i = \frac{i}{l}$ 当且仅当 $i < l+r$。

然后就做完了。

具体证明可以看这里。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+5;
 
int n,l,r,par[maxn],sz[maxn];
int finds(int u) {
    if (par[u] == u) {
        return u;
    }
    return par[u] = finds(par[u]);
}
void unions(int u, int v) {
    u = finds(u), v = finds(v);
    if (u == v) return;
    if (sz[u] < sz[v]) swap(u,v);
    sz[u] += sz[v];
    sz[v] = 0;
    par[v] = u;
}
 
int sg(int i) {
    if (i >= l+r) return 0;
    return i / l;
}
int main() {
    cin >> n >> l >> r;
    for (int i = 1; i <= n; i++) par[i] = i, sz[i] = 1;
    for (int i = 1; i <= n; i++) {
        int u, v; cin >> u >> v;
        unions(u,v);
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        if (par[i] == i) ans ^= sg(sz[i]);
    }
 
    cout << (ans ? "Alice" : "Bob") << "\n";
}