2-SAT

模版

struct Edge {
    int from, to, nxt;
};
int n;  // 变量个数

struct SAT2 {
    // from[u] 代表 u 所在的SCC编号，scc代表scc编号，sz[scc] 代表对应scc的大小
    int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn], head[maxn];
    bool in[maxn];  // instack or not
    int st[maxn], tail = -1, ecnt = 1;
    Edge edges[maxm];
    void dfs(int u) {
        in[u] = 1;
        st[++tail] = u;
        dfn[u] = low[u] = ++id;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int to = edges[e].to;
            if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);  // 要记得在栈内
            if (!dfn[to]) {
                dfs(to);
                low[u] = min(low[u], low[to]);
            }
        }
        if (dfn[u] == low[u]) {
            from[u] = ++scc;
            sz[scc] = 1;
            while (tail >= 0 && st[tail] != u) {
                int cur = st[tail];
                from[cur] = from[u];
                sz[scc]++;
                tail--;
                in[cur] = 0;  // 记得这里，将在栈中的标记去掉
            }
            tail--;
            in[u] = 0;  // 记得这里，将在栈中的标记去掉
        }
    }
    void addEdge(int u, int v) {
        Edge e = {u, v, head[u]};
        head[u] = ecnt;
        edges[ecnt++] = e;
    }

    void solve() {
        for (int i = 1; i <= 2*n; i++) {
            if (!dfn[i]) dfs(i);
        }
        for (int i = 1; i <= n; i++) {
            if (from[i] == from[i+n]) {
                cout << "-1" << "\n";  // 无解
                return;
            }
        }
        // 否则输出答案
        for (int i = 1; i <= n; i++) {
            if (from[i] < from[i+n]) {
                cout << i << "\n";  // 这个变量选择 True
            } else {
                cout << i+n << "\n";  // 这个变量选择 False
            }
        }
    }
};

int f(int u) {
    if (u > n) return u - n;
    return u + n;
}

int main() {
    int T; cin >> T;
    while (T--) {
        SAT2 sat {};  // 注意这里的 {} 才能正确清空！
        cin >> n >> m;
        for (int i = 1; i <= m; i++) {
            int u, v; cin >> u >> v;  // u,v 冲突
            sat.addEdge(u, f(v));   // u -> not v
            sat.addEdge(v, f(u));  // v -> not u
        }
    }
}

介绍

2-SAT 用于解决：寻找满足一个二元 boolean 方程集合的解。

例如，我们有 $n$ 个 boolean 变量 $a_1,a_2,…a_n$。

而我们给出一个boolean方程集合，共有 $m$ 个方程：

$$a_1 \wedge a_3 = 1$$

$$a_1 \vee a_4 = 1$$

$$a_2 \wedge a_4 = 0$$

$$…$$

注意到每一个方程都只有两个变量 $a_i, a_j$，所以叫做 2-SAT。如果有超过 $2$ 个变量，那么是 NP 问题，只能暴力。

• 一般在题目中，当一个元素要么取某一个值，要么取另外一个值（或者状态）时，就可以将这个元素看作一个 boolean 变量，而它的两个值/状态就代表了 2-SAT 中的两个点。

原理

2-SAT 本质上是利用了 boolean 表达式之间的推导关系。

比如 $a_1 \vee a_4 = 1$ 可以等效转化为 $(\neg a_1 \rightarrow a_4) \wedge (\neg a_4 \rightarrow a_1)$。

这意味着，如果 $a_1 = 0$，那么 $a_4 = 1$，且，如果 $a_4 = 0$，那么 $a_1 = 1$。

那么我们就可以这么连边：

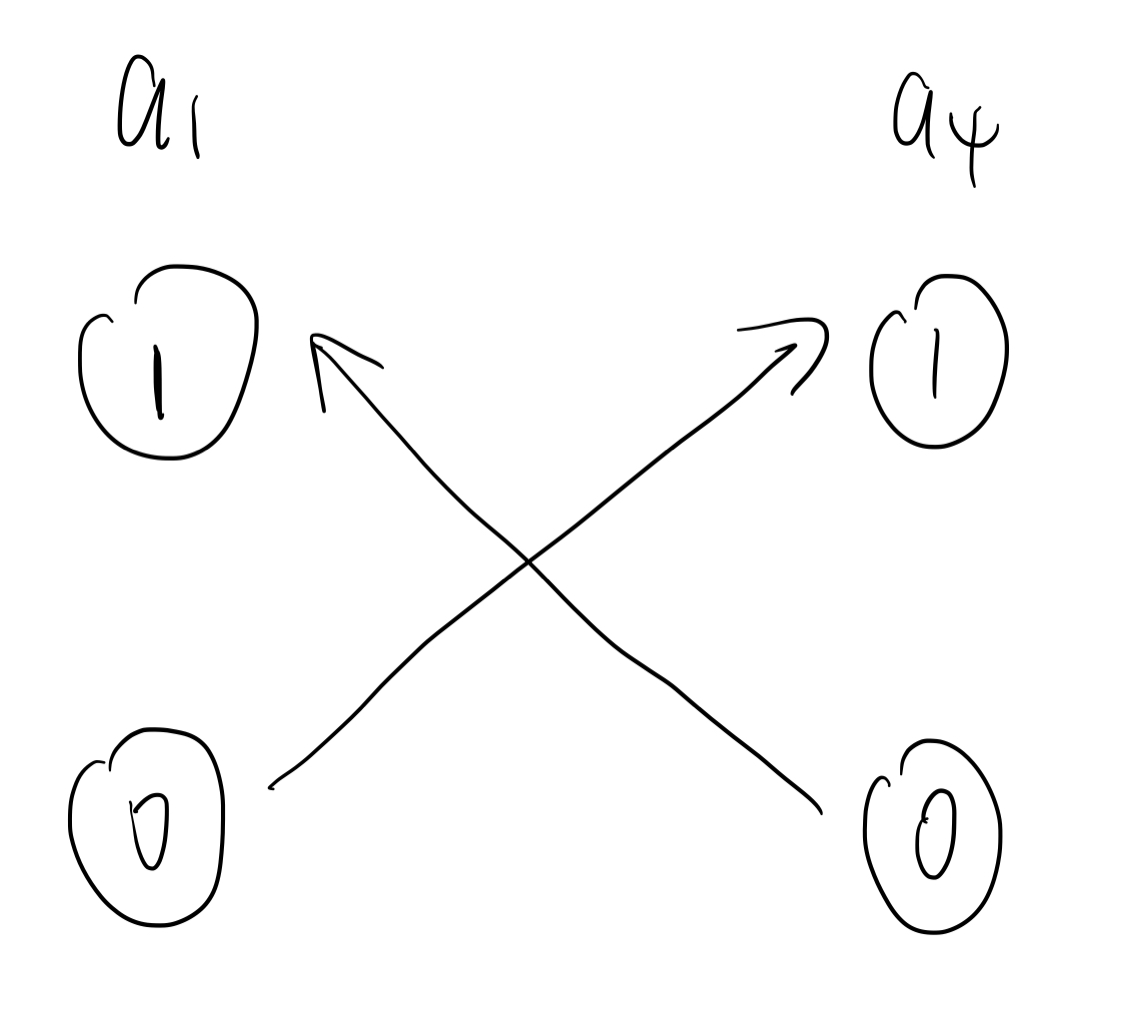
因为是推导关系所以是有向边。

那么 2-SAT 问题有解 $\iff$ 对于所有的 $i$，$a_i$ 和 $\neg a_i$ 并不在同一个强连通分量（SCC）中。

所以跑 tarjan 找SCC即可。

一些例子

考虑如下的情况：

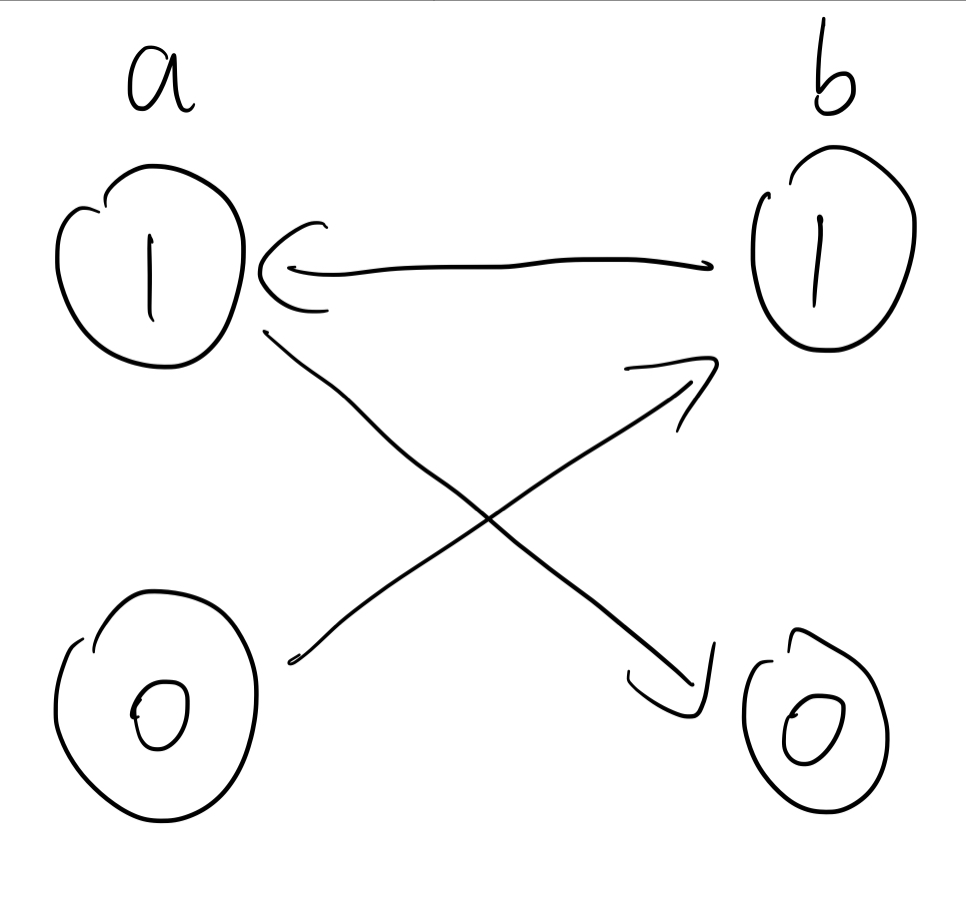
在这个图中，如果我们从 $\neq a$ 出发，最终会走到 $a$。这说明 $\neq a$ 是不可能成立的。

由此可知，$a=1$。

所以我们在找 SCC 过后，还需要判断 $a$ 和 $\neq a$ 的拓扑序。哪个拓扑序更靠后，就说明这个变量必须取这个值。

这样就可以输出解的具体值了。

• 注意到在 tarjan 算法中，SCC的序号反过来就是拓扑序，所以板子中我们直接比较了 from[] 的值，哪个小就取哪个。

常用连边模型

表达式	连边方式
$a \vee b = 1$	$\neg a \rightarrow b, \neg b \rightarrow a$
$a \wedge b = 0$	$a \rightarrow \neg b, b \rightarrow \neg a$
$a = 1$	$\neg a \rightarrow a$
$a = 0$	$a \rightarrow \neg a$
$a,b$ 冲突(不能同时出现)	$a \rightarrow \neg b, b \rightarrow \neg a$

2-SAT的优化建图

在一些特定的问题中，直接建图的复杂度可能过高，需要优化建图后才能跑 2-SAT。

举个例子：

题意

给定 $n$ 个元素，给定 $m$ 个组，每一组有一些元素，一个元素可能属于多个组。

现在要给一些元素加标记，使得每个组都恰好只有一个元素有标记，问这种方案是否存在？

$n,m \leq 10^5$，每个组的元素数量和不超过 $10^6$。

每个元素就两种状态：有标记/无标记，所以每个元素都是一个boolean变量。

然后看每一组：每组内的元素都互相冲突，所以可以用连边的方式来表示。

在一个组内，当任意一个元素有标记了，则其他元素都没有标记，也就是：

$$x_i \rightarrow \neg x_j, \forall j \neq i$$

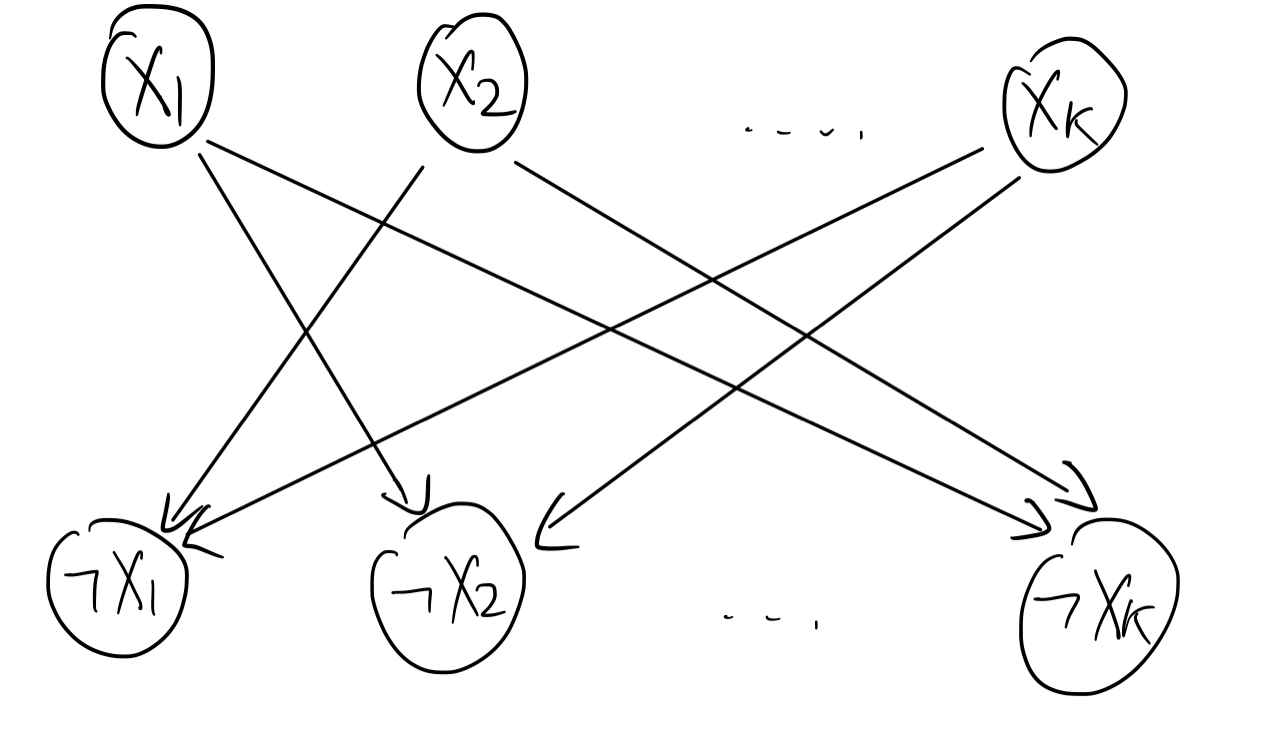
这样连边是 $O(n^2)$ 的，不能接受。

但是注意到，2-SAT中的边是用于表达逻辑推导关系的，也就是说具有传递性，只要有 $a\rightarrow b, b\rightarrow c$，则有 $a \rightarrow c$。

这意味着，从一个点 $x$ 出发，考虑能够到达的所有点 $y$，本质上都相当于直接连了 $x \rightarrow y$ 这条边。

所以我们建 $2n$ 个辅助点，分别代表前缀和后缀。

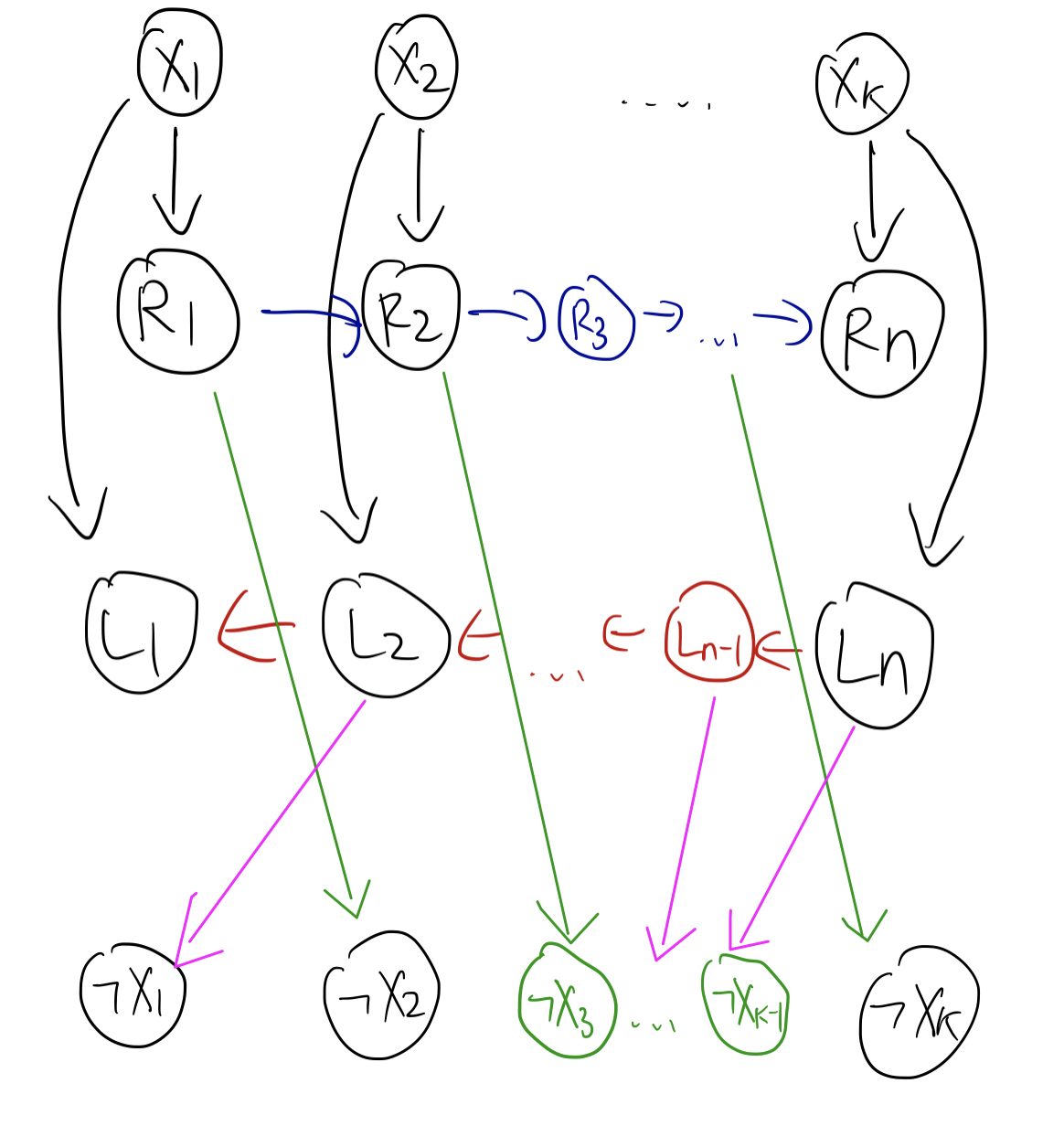
对于每一个 $R_i$，连 $R_i \rightarrow R_{i+1}, R_i \rightarrow \neg X_{i+1}$。
对于每一个 $L_i$，连 $R_i \rightarrow L_{i-1}, L_i \rightarrow \neg X_{i-1}$。
对于每一个 $X_i$，连 $X_i \rightarrow R_i, X_i \rightarrow L_i$。

$R_i$ 代表后缀：从 $R_i$ 出发，就能到达所有的 $\neg X_j, \forall j > i$。

$L_i$ 代表前缀：从 $L_i$ 出发，就能到达所有的 $\neg X_j, \forall j < i$。

相当于 $X_i$ 连上了 $R_i$，就与它右边的所有 $\neg X_j$ 相连了，而连上了 $L_i$，就与它左边的所有 $\neg X_j$ 相连了。

可以发现这个新图和原图等效，在这个新图上跑 2-SAT 即可。

例题

例1 洛谷P5782 [POI2001] 和平委员会

题意

有 $n$ 个党派，每个党派有两个人（第 $i$ 个党派的人是 $2i-1, 2i$）。

给定 $m$ 个关系，表示 $a,b$ 互相厌恶。

现在每个党派需要派出恰好一个人，并且互相厌恶的人不能同时出现。

其中，$n \leq 8000, m \leq 20000$。

题解

本题可以用二分图染色做。

2-SAT 也是可以的。每个党派看作一个 boolean 变量。

参考表达式中的 $a,b$ 冲突就可以做了。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5+5;
const int maxm = 5e5+505;

struct Edge {
    int from, to, nxt;
};
int n;

struct SAT2 {
    // from[u] 代表 u 所在的SCC编号，scc代表scc编号，sz[scc] 代表对应scc的大小
    int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn], head[maxn];
    bool in[maxn];  // instack or not
    int st[maxn], tail = -1, ecnt = 1;
    Edge edges[maxm];
    void dfs(int u) {
        in[u] = 1;
        st[++tail] = u;
        dfn[u] = low[u] = ++id;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int to = edges[e].to;
            if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);  // 要记得在栈内
            if (!dfn[to]) {
                dfs(to);
                low[u] = min(low[u], low[to]);
            }
        }
        if (dfn[u] == low[u]) {
            from[u] = ++scc;
            sz[scc] = 1;
            while (tail >= 0 && st[tail] != u) {
                int cur = st[tail];
                from[cur] = from[u];
                sz[scc]++;
                tail--;
                in[cur] = 0;  // 记得这里，将在栈中的标记去掉
            }
            tail--;
            in[u] = 0;  // 记得这里，将在栈中的标记去掉
        }
    }
    void addEdge(int u, int v) {
        Edge e = {u, v, head[u]};
        head[u] = ecnt;
        edges[ecnt++] = e;
    }

    void solve() {
        for (int i = 1; i <= 2*n; i++) {
            if (!dfn[i]) dfs(i);
        }
        for (int i = 1; i <= 2*n; i += 2) {
            if (from[i] == from[i+1]) {
                cout << "NIE" << "\n";  // 无解
                return;
            }
        }
        // 否则输出答案
        for (int i = 1; i <= 2*n; i += 2) {
            if (from[i] < from[i+1]) {
                cout << i << "\n";
            } else {
                cout << i+1 << "\n";
            }
        }
        // cout << "\n";
    }
} sat;

int m;
int f(int u) {
    if (u % 2 == 0) return u - 1;
    return u + 1;
}
int main() {
    fastio;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v; cin >> u >> v;
        sat.addEdge(u, f(v));
        sat.addEdge(v, f(u));
    }
    sat.solve();
}

例2 CF1250E. The Coronation

题意

给定 $n$ 个 $01$ 串（长度均为 $m$）。

给定一个正整数 $k$，定义两个 $01$ 串为相似当且仅当它们同位置上相同的字符至少有 $k$ 个。

现在我们可以将一些 $01$ 串反转（从后往前）。

求最少翻转多少个，使得所有串之间两两相似？无解输出 $-1$。

其中，$n \in [2, 50], m \in [1, 50], k \in [1,m]$。

题解

这个题 不能用 2SAT！

我们考虑所有两两不相似的串（这个可以直接预处理出来）。

现在其实就相当于，每个串要么翻转，要么不翻转，使得最后得到的 $n$ 个串不能有冲突。

看起来很像 2-SAT，并且也可以这么做？

但有个问题，2-SAT并 没有办法处理最少翻转几个 的问题！

正解是用权值并查集或者二分图染色。

因为这个题是串之间的冲突问题，所以可以这么做，更复杂的情况才需要2-SAT。

考虑二分图染色。

我们将翻转前的所有串作为左边的点，翻转后的作为右边的。

两两冲突的点之间连一条边（$i$ 和翻转后的版本 $i'$ 也要连边）。

虽然这样不算严格的二分图？但跑染色还是没问题的。

连完以后跑染色，可以得到若干个联通块。对于每个联通块，看染色是否成功，如果成功，黑白两个颜色中，翻转后的版本 $i'$ 哪个最少，选最少的那个即可。

如果染色失败，输出无解即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int maxm = 1e5+505;
struct Edge {
    int from, to, nxt;
} edges[maxm];
int n, head[maxn], ecnt = 1;

void addEdge(int u, int v) {
    Edge e = {u, v, head[u]};
    head[u] = ecnt;
    edges[ecnt++] = e;
}

int m, k;
int f(int u) {
    if (u > n) return u - n;
    return u + n;
}

string s[maxn];
int similar(int u, int v) {
    int res = 0;
    for (int i = 0; i < m; i++) {
        if (s[u][i] == s[v][i]) res++;
    }
    return res;
}

vector<int> tmp0, tmp1;
int color[maxn], cnt0, cnt1;
bool ok = 1;
void dfs(int u) {
    if (color[u] == 1 && u > n) tmp1.push_back(u - n);
    if (color[u] == 0 && u > n) tmp0.push_back(u - n);
    for (int e = head[u]; e; e = edges[e].nxt) {
        int v = edges[e].to;
        if (color[v] == -1) {
            color[v] = color[u] ^ 1;
            dfs(v);
        } else if (color[v] == color[u]) {
            ok = 0;
            return;
        }
    }
}

int main() {
    fastio;
    int T; cin >> T;
    while (T--) {
        ok = 1;
        cin >> n >> m >> k;
        for (int i = 1; i <= n; i++) {
            cin >> s[i];
            s[i+n] = s[i];
            reverse(s[i+n].begin(), s[i+n].end());
        }
        for (int i = 1; i <= 2*n; i++) {
            for (int j = i+1; j <= 2*n; j++) {
                if (j == i+n) continue; 
                if (similar(i, j) < k) {  // 冲突
                    addEdge(i, j);
                    addEdge(j, i);
                }
            }
        }
        for (int i = 1; i <= n; i++) addEdge(i, i+n), addEdge(i+n, i);
        vector<int> ans;

        memset(color, -1, sizeof(color));
        for (int i = 1; i <= 2*n; i++) {
            if (color[i] == -1) {
                tmp1.clear(); tmp0.clear();
                color[i] = 0;
                dfs(i);

                if (tmp1.size() < tmp0.size()) {
                    for (int j : tmp1) ans.push_back(j);
                } else {
                    for (int j : tmp0) ans.push_back(j);
                }
            }
        }

        if (!ok) {
            cout << -1 << "\n";
        } else {
            cout << ans.size() << "\n";
            for (int j : ans) cout << j << " ";
            cout << "\n";
        }

        ecnt = 1;
        memset(head, 0, sizeof(head));
        ok = 1;
    }
}

例3 ABC210F. Coprime Solitaire

题意

有 $n$ 张卡片，每张卡片正面写了 $A_i$，背面写了 $B_i$。

求是否存在一种方案，使得所有卡片朝上的那一面的所有数字互质？

其中，$n \leq 3 \times 10^4, A_i,B_i \in [1,2\times 10^6]$。

题解

注意到每张卡片要么正面朝上，要么背面朝上，所以每张卡片都是一个boolean变量 $x$，而正面朝上/背面朝上则分别代表了 $x$ 和 $\neg x$。

但不能枚举 $O(n^2)$ 种卡片pairs，不过可以对于每一个数字进行质因数分解。

每个质数 $p$ 维护一个组，每一组里面有一些数，代表这个数有 $p$ 这个质因数。而这意味着，每一组数里面 最多只能有一个是朝上的。

每一组里面的数有可能是正面的数，也有可能是背面的数。如果是正面的数，就把 $x$ 这个变量放进去，否则把 $\neg x$ 这个变量放进去，这样每一组里面就维护了 $X_1,X_2, …, X_k$ 这些boolean变量。

而每一组的限制条件意味着，每一组里面如果取了 $X_i = 1$，那么其他的 $X_j = 0$。

所以需要 2SAT的优化建图。

对于每一组都进行优化建图即可。由于每一个数最多有 $20$ 个不同的质因子，所以复杂度为 $O(20n)$。

代码

#include <bits/stdc++.h>
using namespace std;
int n, a[maxn], b[maxn];
int f(int u) {
    if (u > n) return u - n;
    return u + n;
}
struct Edge {
    int from, to, nxt;
};

struct SAT2 {
    // from[u] 代表 u 所在的SCC编号，scc代表scc编号，sz[scc] 代表对应scc的大小
    int dfn[maxn], low[maxn], id, from[maxn], scc = 0, sz[maxn], head[maxn];
    bool in[maxn];  // instack or not
    int st[maxn], tail = -1, ecnt = 1;
    Edge edges[maxm];
    void dfs(int u) {
        in[u] = 1;
        st[++tail] = u;
        dfn[u] = low[u] = ++id;
        for (int e = head[u]; e; e = edges[e].nxt) {
            int to = edges[e].to;
            if (dfn[to] && in[to]) low[u] = min(low[u], dfn[to]);  // 要记得在栈内
            if (!dfn[to]) {
                dfs(to);
                low[u] = min(low[u], low[to]);
            }
        }
        if (dfn[u] == low[u]) {
            from[u] = ++scc;
            sz[scc] = 1;
            while (tail >= 0 && st[tail] != u) {
                int cur = st[tail];
                from[cur] = from[u];
                sz[scc]++;
                tail--;
                in[cur] = 0;  // 记得这里，将在栈中的标记去掉
            }
            tail--;
            in[u] = 0;  // 记得这里，将在栈中的标记去掉
        }
    }
    void addEdge(int u, int v) {
        Edge e = {u, v, head[u]};
        head[u] = ecnt;
        edges[ecnt++] = e;
    }

    bool solve() {
        for (int i = 1; i <= 2*n; i++) {
            if (!dfn[i]) dfs(i);
        }
        for (int i = 1; i <= n; i++) {
            if (from[i] == from[i+n]) {
                return 0;
            }
        }
        return 1;
    }
} sat;

const int M = 2e6;
bool isPrime[M+5];
int small[M+5];
vector<int> primes;
int idx[M+5];
vector<int> group[maxn];
void preprocess() {   // 线性筛
    memset(isPrime, 1, sizeof(isPrime));
    small[1] = 1;
    for (int i = 2; i <= M; i++) {
        if (isPrime[i]) primes.push_back(i), small[i] = i;
        for (int j = 0; j < primes.size() && i * primes[j] <= M; j++) {
            int cur = i * primes[j];
            isPrime[cur] = 0;
            small[cur] = primes[j];   // 最小的质因子
            if (i % primes[j] == 0) break;
        }
    }
    for (int i = 0; i < primes.size(); i++) idx[primes[i]] = i;
}

int main() {
    preprocess();
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
    for (int i = 1; i <= n; i++) {
        int x = a[i];
        while (x > 1) {
            int sm = small[x];
            int smidx = idx[sm];
            while (x > 1 && x % sm == 0) x /= sm;
            group[smidx].push_back(i);
        }
        x = b[i];
        while (x > 1) {
            int sm = small[x];
            int smidx = idx[sm];
            while (x > 1 && x % sm == 0) x /= sm;
            group[smidx].push_back(i+n);
        }
    }

    int id = 2*n;
    for (int j = 0; j < primes.size(); j++) {
        int k = group[j].size();
        for (int i = id+1; i <= id+k; i++) {
            int u = group[j][i-id-1];
            if (i < id+k) sat.addEdge(i, f(group[j][i-id])), sat.addEdge(i, i+1);
            if (i > id+1) sat.addEdge(i+k, f(group[j][i-id-2])), sat.addEdge(i+k, i+k-1);
            sat.addEdge(u, i);
            sat.addEdge(u, i+k);
        }
        id += 2*k;
    }
    cout << (sat.solve() ? "Yes" : "No") << "\n";
}