三元环计数

介绍

给定一个无向图，找出图中所有的三元环，每个环只能被计一次。(比如 $a,b,c$ 和 $b,a,c$ 都是同一个环)。

我们先处理出每个点的 degree，然后建一个新的图，这个图是有向图：

$u \rightarrow v$ 连一条边当且仅当以下条件之一成立：

$d_u < d_v$
$d_u = d_v$ 且 $u<v$。

其中，$d_u$ 是 $u$ 的degree。

然后利用如下代码片段进行计数：

vector<int> adj[maxn];
int deg[maxn];
int n,m;
int vis[maxn];

// check (u,v) 这条边是否满足以下条件之一: 
// (1) deg(u) < deg(v)
// (2) deg(u) == deg(v) && u < v
bool valid(int u, int v) {
    return deg[u] < deg[v] || (deg[u] == deg[v] && u < v);
}

vector<int> adj2[maxn];
void count_cycle() {
    for (int a = 1; a <= n; a++) {
        for (int b : adj[a]) {
            if (valid(a,b)) adj2[a].push_back(b);
        }
    }

    for (int a = 1; a <= n; a++) {
        for (int b : adj2[a]) vis[b] = a;  // 打上时间戳

        for (int b : adj2[a]) {
            for (int c : adj2[b]) {
                if (vis[c] == a) {
                    // (a,b,c) 是一个环
                    ...
                }
            }
        }
    }
}

这段代码本质上是枚举了一条边 $(a,b)$，然后找和 $a,b$ 均相连的点 $c$。

首先正确性不难证明，由于我们按照如上定义得出了一个新的有向图，所以每个环只会被记录一次。

时间复杂度是 $O(m \sqrt m)$，以下是证明：

第一步是枚举边 $a,b$，这是 $O(m)$ 的，然后我们讨论 $b$ 是一个大点（$d_b > \sqrt m$）还是一个小点（$d_b \leq \sqrt m$）。

如果 $b$ 是大点，意味着这样的 $b$ 最多就 $\sqrt m$ 个，而 $d_c \geq d_b$，所以 $c$ 也是大点，这意味着这样的 $c$ 最多也就 $\sqrt m$ 个。所以里层循环枚举 $c$ 的复杂度是 $O(\sqrt m)$，总共 $O(m \sqrt m)$。
如果 $b$ 是小点，那么很明显 $d_b \leq \sqrt m$，由于 $c$ 是 $b$ 的邻居，这意味着这样的 $c$ 不超过 $d_b = \sqrt m$ 个，所以里层循环枚举 $c$ 的复杂度是 $O(\sqrt m)$，总共 $O(m \sqrt m)$。

例题

例1 NAQ2021 L. Sword Counting

题意

给定一个无向图，求形状为如下图的 subgraph 数量：

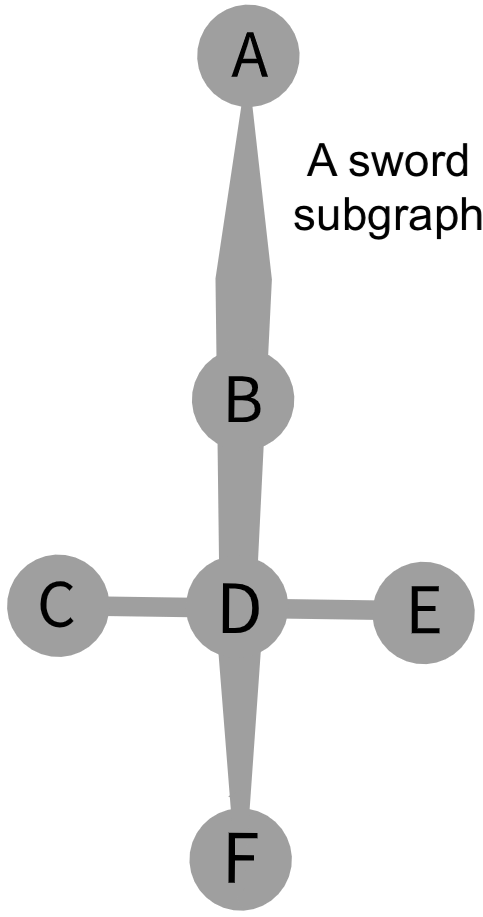
其中，$n,m \leq 10^5$，两个subgraph被看作不同当且仅当存在至少一条边不同。

题解

先找 $D$，特征是 $d_D \geq 4$，再找 $B$，特征是 $d_B \geq 2$。

确认完这两个点以后，我们要判断剩下 $A,C,E,F$ 有多少种选法。

首先注意到，如果 $A$ 同时是 $B,D$ 的一个邻居，那么选了 $A$ 以后会让 $D$ 剩下的选择少一个，否则没有影响。

所以我们只要找出 $B,D$ 共同的邻居数量，假设 $B,D$ 共同邻居共有 $x$ 个，那么答案为：

$$(d_B-1-x)C_{d_D-1}^3 + xC_{d_D-2}^3$$

这个 $x$ 怎么找？就找到所有的三元环即可。

代码

#include <bits/stdc++.h>
using namespace std;
ll C3(ll a) {
    if (a < 3) return 0;
    return a * (a-1) * (a-2) / 6;
}

vector<int> adj[maxn];
int deg[maxn];
map<int, int> cnt[maxn];  // cnt[a][b]: a,b的共同邻居数量, a<b

int n,m;
int vis[maxn];

// check (u,v) 这条边是否满足以下条件之一: 
// (1) deg(u) < deg(v)
// (2) deg(u) == deg(v) && u < v
bool valid(int u, int v) {
    return deg[u] < deg[v] || (deg[u] == deg[v] && u < v);
}

vector<int> adj2[maxn];
void count_cycle() {
    for (int a = 1; a <= n; a++) {
        for (int b : adj[a]) {
            if (valid(a,b)) adj2[a].push_back(b);
        }
    }

    for (int a = 1; a <= n; a++) {
        for (int b : adj2[a]) vis[b] = a;

        for (int b : adj2[a]) {
            for (int c : adj2[b]) {
                if (vis[c] == a) {
                    // (a,b,c) 是一个环
                    cnt[min(a,b)][max(a,b)]++;
                    cnt[min(a,c)][max(a,c)]++;
                    cnt[min(b,c)][max(b,c)]++;
                }
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v; cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
        deg[u]++, deg[v]++;
    }

    count_cycle();

    ll ans = 0;
    for (int d = 1; d <= n; d++) {
        if (deg[d] < 4) continue;
        for (int b : adj[d]) {
            if (deg[b] < 2) continue;
            int x = cnt[min(d,b)][max(d,b)];
            ans = ans + C3(deg[d]-2) * x + max(0, deg[b] - 1 - x) * C3(deg[d]-1);
        }
    }
    cout << ans << endl;
}

Contents

介绍

例题

例1 NAQ2021 L. Sword Counting